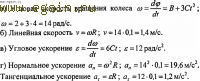– угловое ускорение, выраженное через обороты, число оборотов можно представить в виде n к = n 0 + e" t и тогда

http://pandia.ru/text/80/153/images/image553.gif" width="201" height="37 src=">

что соответствует

n1 = 2 × 60 = 120 об/мин.

Теперь находим при этой скорости вращения маховика скорость точек на его ободе:

http://pandia.ru/text/80/153/images/image555.gif" width="236" height="20 src=">

Задача 45. Вал, вращающийся равноускоренно из состояния покоя, в первые 12 с совершает 95,5 оборота. С каким угловым ускорением вращается вал и какую угловую скорость он приоб­ретает?

Решение.

1. Угловое перемещение за время t =12 с равноускоренного движения составляет

http://pandia.ru/text/80/153/images/image557.gif" width="197" height="39 src=">

3. К концу 12-й секунды вал приобретает угловую скорость:

http://pandia.ru/text/80/153/images/image559.gif" width="180" height="37 src=">

Задача 46. Колесо, вращающееся с частотой 1500 об/мин, при торможении начинает вращаться равнозамедленно и через 30 с останавливается. Определить угловое ускорение и число оборотов колеса с момента начала торможения до остановки.

Решение.

1. Выразим начальную угловую скорость в рад/с:

http://pandia.ru/text/80/153/images/image561.gif" width="208" height="37 src=">

2. Определим число оборотов в виде

http://pandia.ru/text/80/153/images/image563.gif" width="263" height="36 src=">

Задача 47. Вращение вала в течение первых 20с проис­ходит согласно уравнению j = 0,8 t3.

Определить угловую скорость вала в конце 20-й секунды; угло­вое ускорение в начале движения, в конце 10-й и 20-й секунд; сколько всего оборотов делает вал за 20 с.

Решение.

1. Определим число оборотов вала за 20с. Для этого пред­варительно найдем угол поворота за t = 20 с:

http://pandia.ru/text/80/153/images/image565.gif" width="199" height="37 src=">

2. Определим уравнение угловой скорости вала:

http://pandia.ru/text/80/153/images/image567.gif" width="195" height="23 src=">

Если выразить эту угловую скорость в об/мин, то

http://pandia.ru/text/80/153/images/image569.gif" width="132" height="37 src=">

5. Найдем угловое ускорение в начале движения (t 0= 0), в конце 10- й (t1 = 10 с) и 20-й секунд (t2 = 20 с):

http://pandia.ru/text/80/153/images/image571.gif" width="187" height="23 src=">

Глава 5. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ

§ 20. Абсолютное движение и его составляющие

В предыдущих главах мы рассматривали движение точки и тела относительно системы отсчета, связанной с Землей, которую условно считали неподвижной. Движение относительно этой «неподвижной» системы координат принято называть абсо­лютным. Но иногда приходится рассматривать движение точки относительно системы, связанной с телом, которое само движется относительно Земли или тел, неподвижно скрепленных с ней (стены здания, рельсы, машины и т. п.). В этом случае абсолютное движение точки удобно представить себе как сложное движение, состоящее из двух (или более) независимых движений.

Получить полный текст

Движение точки относительно подвижной системы отсчета называют относительным, а движение точки вместе с подвижной системой отсчета относительно неподвижной системы отсчета называют переносным.

Для примера рассмотрим движение поднимаемого при помощи крана груза в условиях, когда стрела крана одновременно пово­рачивается вокруг своей оси. Движущейся системой отсчета в этом случае является стрела крана. Относительно нее груз движется прямолинейно вверх – это относительное движение. Одновремен­но вместе со стрелой груз совершает движение по дуге окружно­сти относительно «неподвижной» Земли – это переносное движе­ние груза.

Наблюдатель, стоящий на Земле, видит абсолютное движение груза, складывающееся из двух происходящих одновременно дви­жений.

Сложным также является движение человека по движущейся лестнице эскалатора: движение человека по отношению к ступеням является относительным, а перемещение его вместе со ступенями относительно неподвижных стен тоннеля является переносным. Абсолютным будет движение человека относительно неподвижных стен.

Таким образом, абсолютное движение точки – совокупность двух движений: относительного и переносного. При этом разли­чают абсолютную, относительную и переносную траектории и соответственно такие же скорости и ускорения точки.

§21. Сложение скоростей и ускорений точки
в сложном движении

В ряде случаев по заданным относительному и переносному движениям определяют абсолютное движение точки. Иногда зада­ны абсолютное и одно из составляющих движений, а необходимо определить другое составляющее движение.

Рассмотрим, как определяют абсолютное движение точки (т. е. абсолютные перемещения, скорость и ускорение), если ее отно­сительное и переносное движения прямолинейны и направлены под углом друг к другу. Пусть груз М движется вниз по наклонной плоскости и за промежуток времени D t перемещается относительно нее на D Sотн (рис. 72).

/text/categ/nauka.php" class="myButtonNauka">Получить полный текст

http://pandia.ru/text/80/153/images/image574.jpg" width="268" height="83 src=">

Поделим каждый член уравнения (37) на время D t , в течение которого происходило движение, и устремляя D t ® 0, получим выражение:

http://pandia.ru/text/80/153/images/image576.gif" width="101" height="24 src=">. (38)

Следовательно, в случае, если относительное и переносное движения прямолинейны, абсолютная скорость точки в каждый момент времени определяется как геометрическая сумма относи­тельной и переносной скоростей. Графически абсолютная скорость точки может быть определена по правилу параллелограмма или треугольника (рис. 74, а и б).

http://pandia.ru/text/80/153/images/image578.gif" width="251" height="31 src=">

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ

Кинематика вращения тела вокруг неподвижной оси

1. Краткие сведения из теории

Уравнение вращательного движения твердого тела вокруг неподвижной оси имеет вид

Отсчет угла ведется от выбранного начала. При этом углам, отложенным в направлении движения часовой стрелки, придается знак “минус”, а углам противоположного направления – знак “плюс”.

Угол поворота выражается в радианах. Иногда угол поворота определяется числом оборотов N . Зависимость между и N следующая .

Угловая скорость тела:

Знак производной дает возможность установить происходит ли вращение тела в положительном направлении отсчета угла поворота (знак “плюс”) или в обратную сторону (знак “минус”). Единица измерения угловой скорости – радиан в секунду (или 1/с).

Иногда угловую скорость характеризуют числом оборотов в минуту и обозначают буквой n . Зависимость между и n имеет вид

Угловое ускорение тела:

(42)

Знак производной дает возможность установить является ли вращение тела в данный момент времени ускоренным или замедленным. Если знаки и одинаковы, тело вращается ускоренно, а если их знаки различны – замедленно. Единица измерения углового ускорения – радиан на секунду в квадрате (или 1/с 2 ).

Траекториями точек тела, не лежащих на оси вращения, являются окружности с центрами на оси вращения и радиусами, равными кратчайшему расстоянию от этих точек до оси вращения.

Модуль скорости любой точки тела, находящейся на расстоянии h от оси вращения (рис. 18), определяется по формуле

. (43)

Направлена скорость точки по касательной к описываемой точкой окружности в сторону движения.

Ускорение любой точки тела состоит из двух составляющих – вращательного и осестремительного ускорений:

Модуль вращательного ускорения точки определяется по формуле

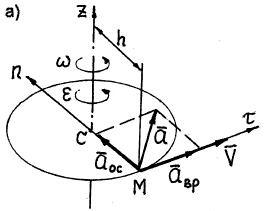
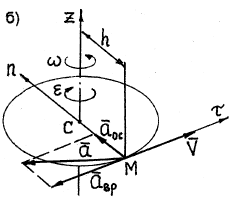
Рис. 18

Вращательное ускорение направлено по касательной к описываемой точкой окружности в ту же сторону, что и его скорость, если вращение тела ускоренное (рис. 18, а) и в сторону, противоположную скорости, если вращение замедленное (рис.18, б).

Модуль осестремительного ускорения определяется по формуле

Осестремительное ускорение всегда направлено по радиусу окружности от точки к центру окружности (рис. 18).

Модуль полного ускорения точки определяется по формуле

(46)

2. Основные типы задач кинематики вращения тела вокруг оси

В зависимости от того, что задано в условии задачи и что требуется определить, различают следующие два основных типа задач.

1. Исследуется движение тела в целом. В этих задачах вначале нужно получить законы (40)–(42) и, используя связь между ними, определить требуемую величину (см. примеры 17 и 18).

2. Требуется определить скорости и ускорения отдельных точек тела. Для решения задач этого типа вначале надо установить кинематические характеристики движения всего тела в целом, т.е. найти , и . После чего по формулам (43), (44), (45), (46) определить скорости и ускорения точек тела (см. пример 19).

Пример 17. Пропеллер самолета, делающий 1200 об /мин , после выключения двигателя останавливается через 8 с. Сколько оборотов сделал пропеллер за это время, если считать его вращение равнозамедленным?

Решение:

Вначале получим законы вращения пропеллера (40), (41) и (42). По условию задачи пропеллер вращается равнозамедленно , из этого следует, что

Поэтому

(48)

Начальной угловой скоростью при замедленном вращении будет та, которую пропеллер имел до выключения двигателя. Следовательно, . В момент остановки при t 1 = 8 сек. угловая скорость тела . Подставляя эти значения в уравнение (47), получим

Отсюда

Если обозначить число сделанных пропеллером за время t 1 оборотов через N 1 , то угол поворота за то же время будет равен

Подставляя найденные значения и в уравнение (48), получим

Отсюда оборотов.

Пример 18. Найти закон вращения тела вокруг оси, если известны следующие данные: угловая скорость изменяется пропорционально t 2 , начальный угол поворота рад, для заданного момента времени t 1 = 3 с угловое ускорение 1/с 2 .

Решение:

По условию задачи модуль угловой скорости изменяется пропорционально t 2 . Обозначая неизвестный коэффициент пропорциональности буквой k , имеем

Найдем , беря производные по времени от обеих частей равенства (49),

Определим коэффициент k из условия, что при t 1 = 3 сек. угловое ускорение 1/с 2 : или

Подставляя значение k в уравнение (49), получим

Учитывая, что , будем иметь

Умножая обе части этого уравнения на dt и интегрируя, находим

В начальный момент при t = 0, = 2 рад, следовательно, c = 2.

Таким образом, радиан.

Пример 19. В период разгона ротор электродвигателя вращается по закону , где t в сек, в рад.

Определить в конце 4-й секунды линейную скорость, вращательное, осестремительное и полное ускорения точки, лежащей на ободе ротора, если диаметр ротора D = 40 см .

Решение:

По заданному уравнению вращения ротора находим его угловую скорость и угловое ускорение , .

Подставляя значение t 1 = 4 сек в выражение для и , найдем

1/с,

1/с2 .

Определим модули линейной скорости, вращательного и осестремительного ускорений в этот же момент времени по формулам (43), (44) и (45)

Модуль полного ускорения точки обода ротора определим по формуле (46)

3. Определение скоростей и ускорений в случаях, когда вращающееся тело входит в состав различных механизмов

Рассмотрим механизмы с поступательным и вращательным движением звеньев. Решение задачи начинают с определения скоростей точек того звена, для которого движение задано. Затем рассматривают звено, которое присоединено к первому звену и т.д. В результате определяют скорости точек всех звеньев механизма. В такой же последовательности определяют и ускорения точек.

Передача вращения от одного вращающегося тела, называемого ведущим, к другому, называемому ведомым, может осуществляться при помощи фрикционной или зубчатой передачи (рис. 19).

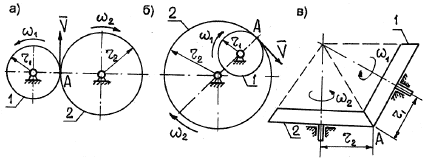
Рис. 19

Во фрикционной передаче вращение передается вследствие действия силы трения в месте контакта соприкасающихся колес, в зубчатой передаче – от зацепления зубьев. Оси вращения ведущего и ведомого колес могут быть параллельными (рис. 19, а, б) или пересекаться (рис. 19, в). В рассмотренных случаях линейные скорости точек А соприкасания колес одинаковы, их модули определяются так:

. (50)

Отсюда. (51)

То есть угловые скорости колес фрикционной или зубчатой передачи обратно пропорциональны радиусам колес.

При преобразовании вращательного движения в поступательное (или наоборот) часто используют зацепление зубчатого колеса с зубчатой рейкой (рис. 20). Для этой передачи выполняется условие: .

Кроме фрикционной и зубчатой передач, существует передача вращения при помощи гибкой связи (ремня, троса, цепи) (рис. 21).

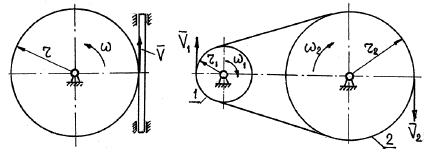
Рис. 20 Рис. 21

Так как модули скоростей всех точек ремня одинаковы и ремень не скользит по поверхностям шкивов, то соотношения (50) и (51) относятся и к ременной передаче.

Пример 20. В механизме домкрата при вращении рукоятки ОА шестерни 1, 2, 3, 4, 5 приводят в движение зубчатую рейку ВС домкрата (рис. 22).

Определить скорость рейки, если рукоятка ОА делает 30 оборотов в минуту (n = 30 об /мин). Числа зубцов шестерен: z 1 = 6,z 2 = 24,z 3 = 8,z 4 = 32; радиус пятой шестерни r 5 = 4 см .

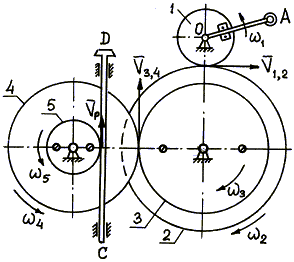
Рис. 22

Решение:

Так как рукоятка ОА жестко соединена с шестерней 1, то последняя делает тоже 30 об /мин или

Модули скоростей точек соприкасания зубчатых колес 1 и 2 одинаковы для точек обоих колес и определяются по формуле (50)

Отсюда (см. также (51)).

Так как числа зубьев пропорциональны радиусам колес, то .

Отсюда

Шестерни 2 и 3 жестко соединены между собой, поэтому

Для находящихся в зацеплении колес 3 и 4 на основании (51) можно записать

Отсюда

Шестерни 4 и 5 жестко соединены между собой, поэтому

Модули скоростей точек соприкосновения зубчатой рейки ВС и шестерни 5 одинаковы, поэтому

или

Пример 21. Рейка 1, ступенчатое колесо 2 с радиусами R 2 и r 2 иколесо 3 радиуса R 3 , скрепленное с валом радиуса r 3 , находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис.23). Рейка движется по закону

Дано: R 2 =6 см, r 2 =4 см, R 3 =8 см, r 3 =3 см, (S - в сантиметрах, t - в секундах),А - точка обода колеса 3, t 1 =3 с. Определить: , , , в момент времени t = t 1 .

Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдельные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R (рис. 6). Ее положение через промежуток времени Dr зададим углом Dj. Элементарные (бесконечно малые) повороты можно рассматривать как векторы (они обозначаются или ). Модуль вектора равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т. е. подчиняется правилу правого винта (рис. 6). Векторы, направления которых связываются с направлением вращения, называются псевдовекторами или аксиальными векторами. Эти векторы не имеют определенных точек приложения: они могут откладываться из любой точки оси вращения.

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

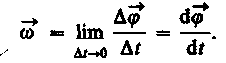
Вектор направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор (рис. 7). Размерность угловой скорости , а ее единица - радиан в секунду (рад/с).

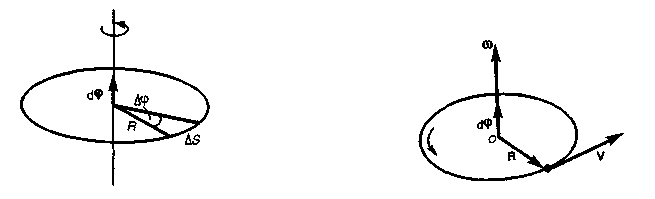
Рис. 6 Рис. 7

Линейная скорость точки (см. рис. 6)

.

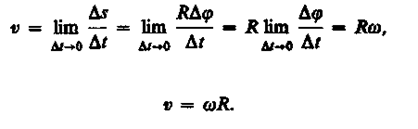
В векторном виде формулу для линейной скорости можно написать как векторное произведение:

При этом модуль векторного произведения, по определению, равен еаКяп(шК) а направление совпадает с направлением поступательного движения правого винта при его вращении от к R.

Если w =const, то вращение равномерное и его можно характеризовать периодом вращения Т - временем, за которое точка совершает один полный оборот, т. е поворачивается на угол 2p. Так как промежутку времени Dt = Т соответствует Dj = 2p, то w = 2p/Т,откуда

Число полных оборотов, совершаемых телом при равномерном его движении пс окоужности, в единицу времени называется частотой вращения:

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

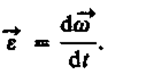
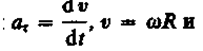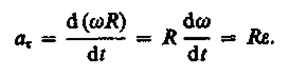Тангенциальная составляющая ускорения

Нормальная составляющая ускорения

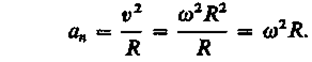
При вращении тела вокруг неподвижной оси вектор углового ускорения направлю вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор сонаправлен вектору (рис. 8), при замедлен ном - противонаправлен ему (рис. 9).

Рис. 8 Рис. 9

Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение а t , нормальное ускорение а n) и угловыми величинами (угол поворота j, угловая скорость w, угловое ускорение e) выражается следующими формулами:

В случае равнопеременного движения точки по окружности (e-const)

где w 0 - начальная угловая скорость.

Задачи

1.1.Зависимость пройденного телом пути от времени задается уравнением s=A+Bt+Ct 2 +Dt 3 (С=0,1 м/с 2 , D=0,03 м/с 3). Определить: 1) время после начала движения, через которое ускорение а тела будет равно 2 м/с 2 ;

2) среднее ускорение <а> тела за этот промежуток времени.

1.2. Пренебрегая сопротивлением воздуха, определить угол, под которым тело брошено к горизонту, если максимальная высота подъема тела равна 1/4 дальности его полета.

1.3.Колесо радиусом R = 0,1 м вращается так, что зависимость угловой скорости от времени задается уравнением w= 2At + 5Bt 4 (А = 2 рад/с 2 и В = 1 рад/с 5). Определить полное ускорение точек обода колеса через t = 1 с после начала вращения и число оборотов, сделанных колесом за это время. [а=8,5 м/с 2 ; N = 0,48]

1.4.Нормальное ускорение точки, движущейся по окружности радиусом г=4 м, задается уравнением a n =A+Bt+Ct 2 (A = 1 м/с 2 , B = 6 м/с 2 , С = 3 м/с 2). Определить: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время t 1 =5 с после начала движения; 3) полное ускорение для момента времени t 2 =1 с.

1.5.Частота вращения колеса при равнозамедленном движении за t = 1 мин уменьшилась от 300 до 180 мин -1 . Определить: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.

1.6.Диск радиусом R=10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением j=A+3t+Ct 2 +Dt 3 (B = 1 рад/с, С = 1 рад/с 2 , D = 1 рад/с 3). Определить для точек на ободе колеса к концу второй секунды после начала движения: 1) тангенциальное ускорение %; 2) нормальное ускорение а n ; 3) полное ускорение а.

1.56. Точка движется по окружности радиусом R = 2см. Зависимость пути от времени дается уравнением s = С/3, где С = 0,1 см/с3. Найти нормальное аn и тангенциальное аt ускорения точки в момент, когда линейная скорость точки v = 0,3 м/с.
Решение:

1.57. Точка движется по окружности так, что зависимость пути от времени дается уравнением s = A-Bt + Ct^2, где В = 2 м/с и С = 1 м/с2. Найти линейную скорость v точки, ее тангенциальное at, нормальное an и полное а ускорения через время t = 3 с после начала движения, если известно, что при t’ = 2 с нормальное ускорение точки а’н = 0,5 м/с2.
Решение:

1.58. Найти угловое ускорение s колеса, если известно, что через время t = 2 с после начала движения вектор полного ускорения точки, лежащей на ободе, составляет угол а = 60° с вектором ее линейной скорости.
Решение:

1.59. Колесо вращается с угловым ускорением E=2 рад/с2. Через время t = 0,5 с после начала движения полное ускорение колеса а = 13,6 см/с". Найти радиус R колеса.
Решение:

1.60. Колесо радиусом R = 0,1м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением (р = А + Bt + Сt^2, где В =2рад/с и С = 1 рад/с^3. Для точек, лежащих на ободе колеса, найти через время t = 2 с после начала движения:
а) угловую скорость w;
б) линейную скорость v;
в) угловое ускорение E ;
г) тангенциальное at и нормальное an ускорения.
Решение: