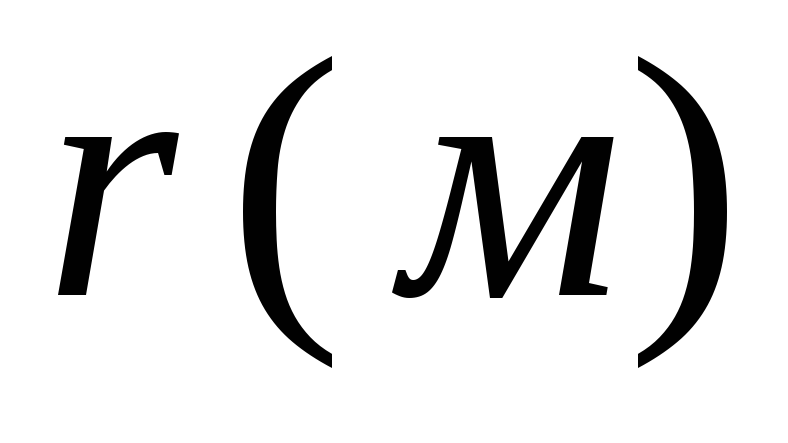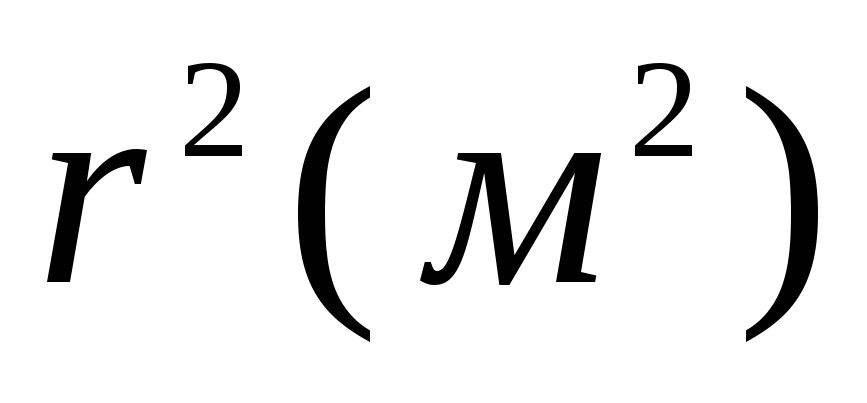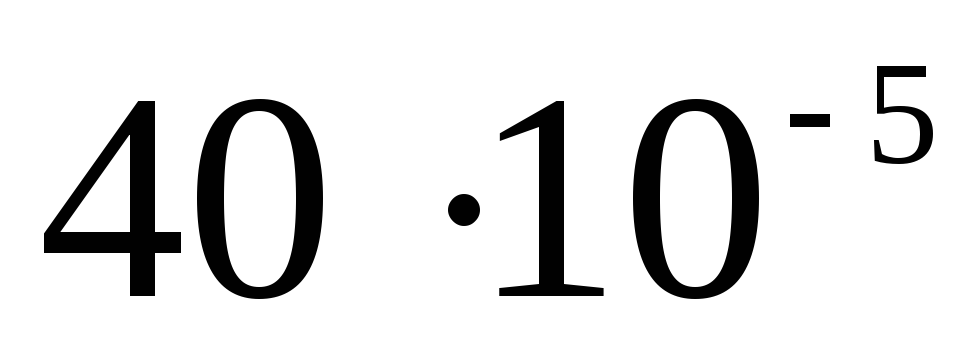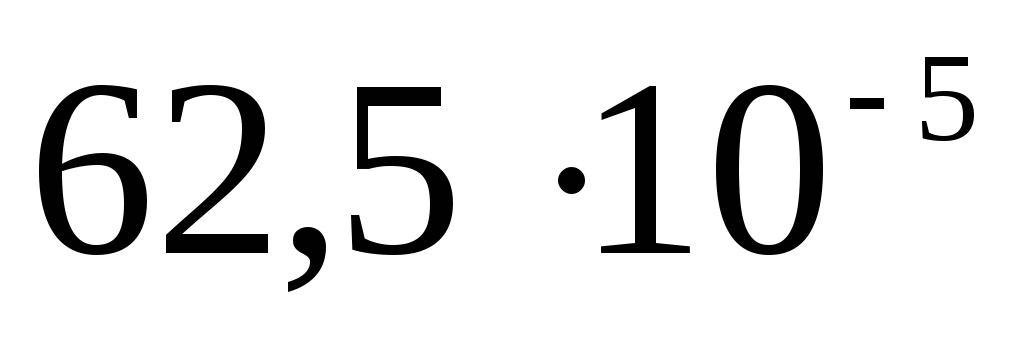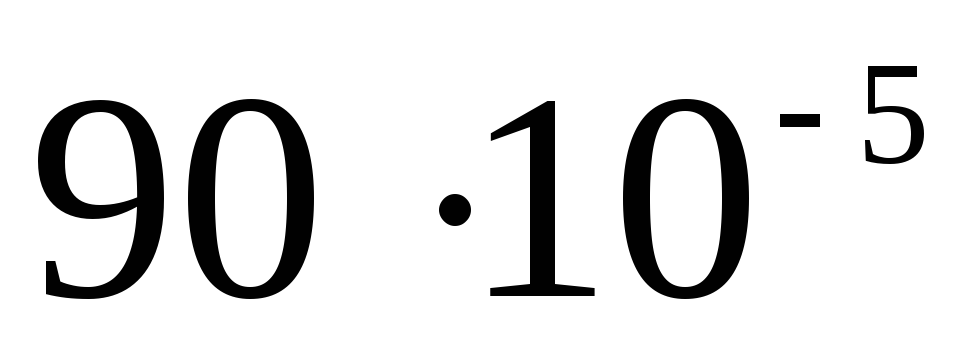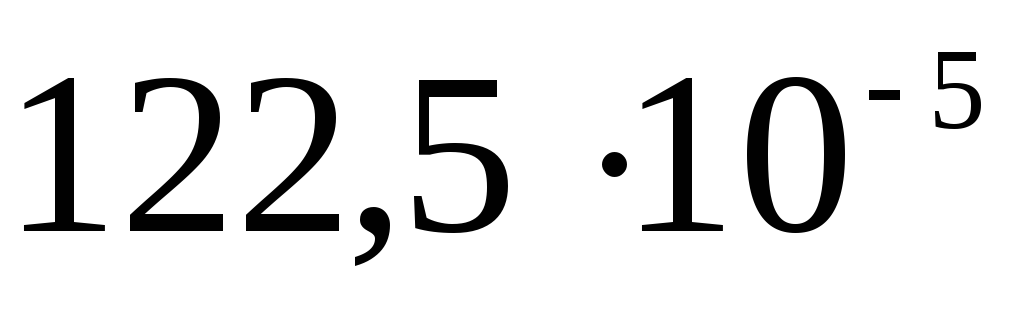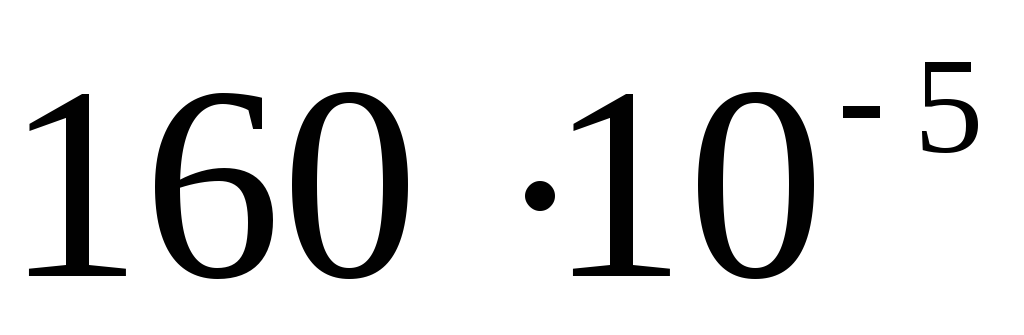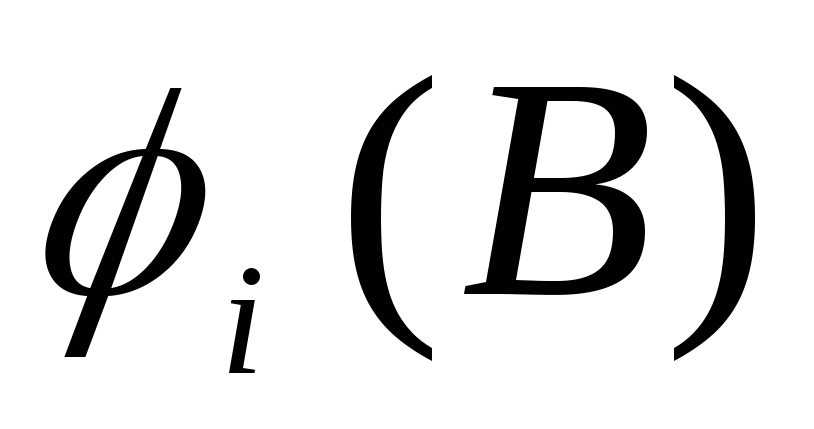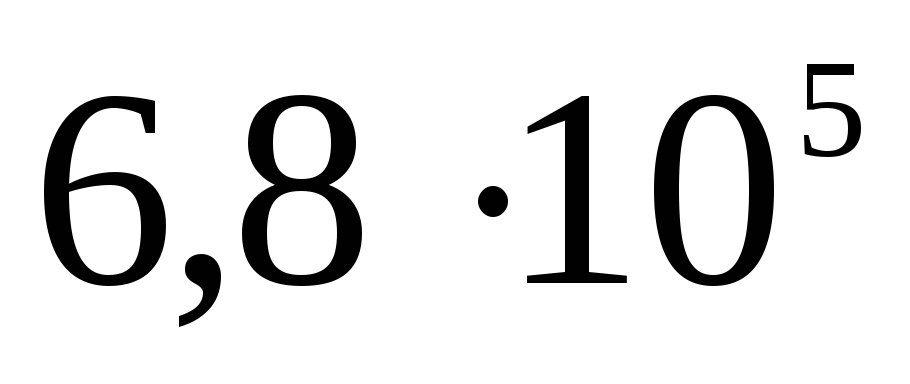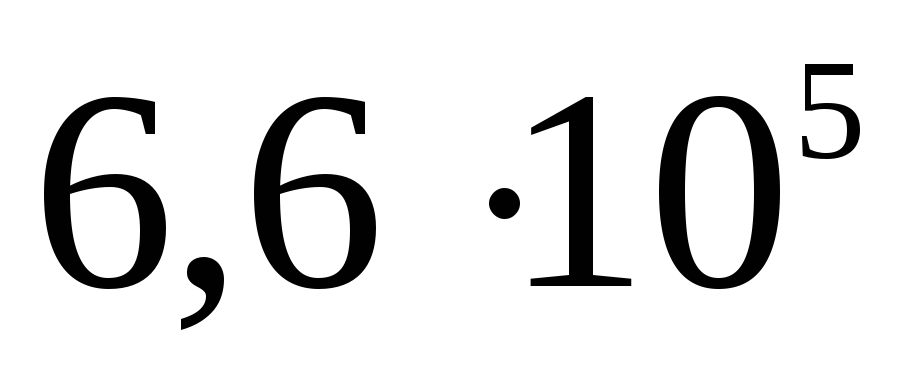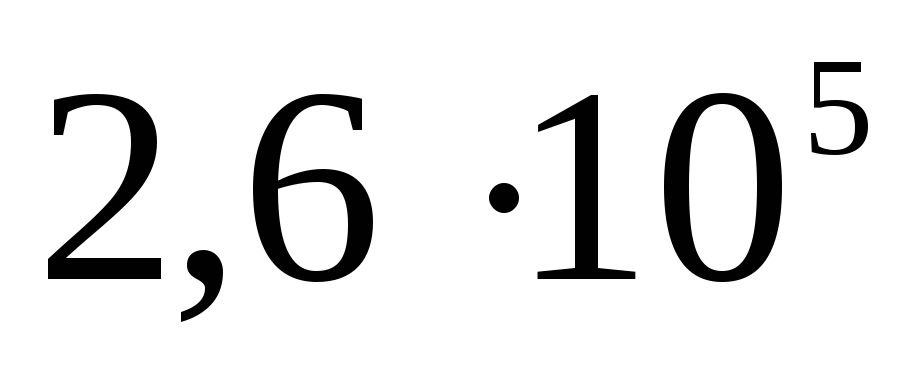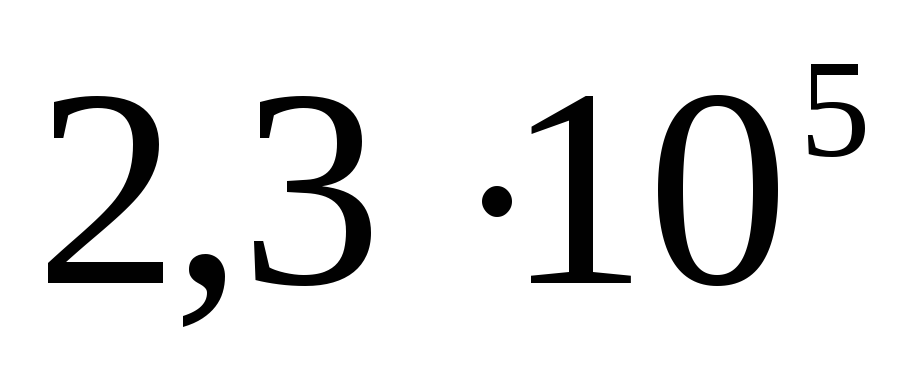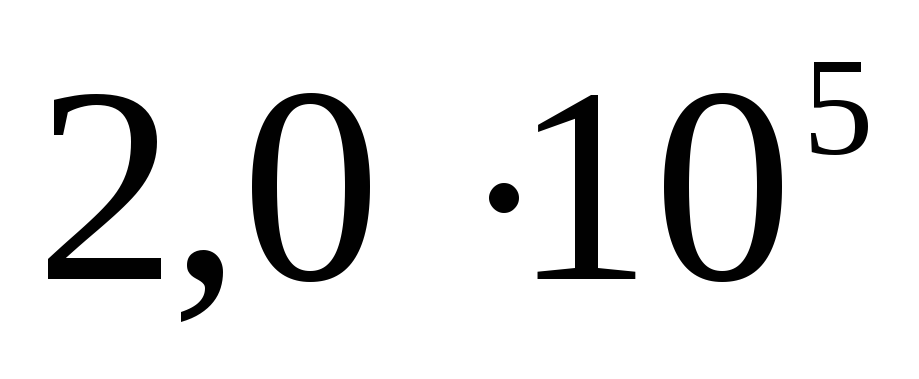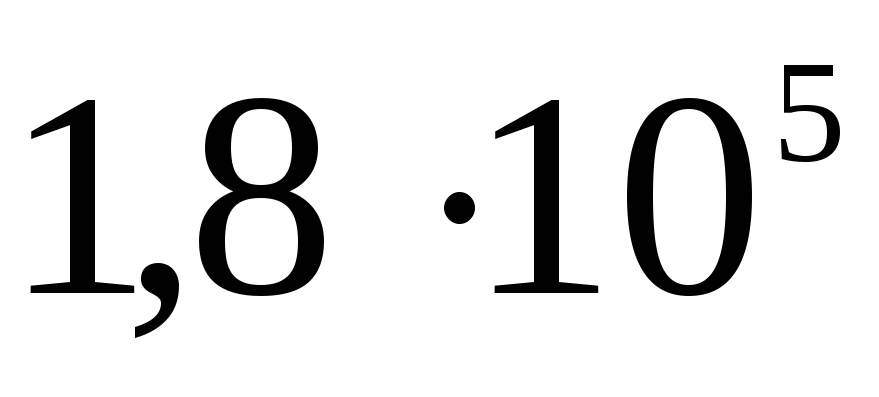Elektrostatika
1
(CT 2001 Test 9. A19). Vadošās lodītes rādiuss R
ir pozitīvs lādiņš +
q
. Ja 2 attālumā R no lodītes centra novieto punktu negatīvu lādiņu -2 q, tad potenciāls bumbas centrā
Bieža kļūda risinot, tas izriet no nepareizas formulējuma interpretācijas: "vadošās bumbas iekšpusē nav lauka." No šī apgalvojuma tiek izdarīts kļūdains secinājums: abi lauka raksturlielumi: gan intensitāte, gan potenciāls ir vienādi ar nulli. Faktiski šajā gadījumā tikai lauka stiprums ir vienāds ar nulli, jo bezmaksas maksas pārstāj kustēties pa vadītāja virsmu, kad vektors  jebkurā virsmas punktā ir tai perpendikulāra. Vadītāja virsma šajā gadījumā ir ekvipotenciāls. Pārbaudes lādiņa pārvietošanas darbs tilpumā, ko ierobežo virsma, ir nulle, jo spēks, kas iedarbojas uz lādiņu, ir vienāds ar nulli; no tā izriet, ka, pārvietojoties no punkta uz punktu, lādiņa potenciālā enerģija nemainās: elektriskais potenciāls tilpumā, ko ierobežo vadoša virsma, ir nemainīgs un vienāds ar potenciālu uz pašas virsmas. Uzlādētas sfēras intensitātes un potenciāla izmaiņas ar attālumu no lādiņa centra var ilustrēt ar grafikiem (sk. att.).
jebkurā virsmas punktā ir tai perpendikulāra. Vadītāja virsma šajā gadījumā ir ekvipotenciāls. Pārbaudes lādiņa pārvietošanas darbs tilpumā, ko ierobežo virsma, ir nulle, jo spēks, kas iedarbojas uz lādiņu, ir vienāds ar nulli; no tā izriet, ka, pārvietojoties no punkta uz punktu, lādiņa potenciālā enerģija nemainās: elektriskais potenciāls tilpumā, ko ierobežo vadoša virsma, ir nemainīgs un vienāds ar potenciālu uz pašas virsmas. Uzlādētas sfēras intensitātes un potenciāla izmaiņas ar attālumu no lādiņa centra var ilustrēt ar grafikiem (sk. att.).
Risinājums
Potenciāls, ko rada sfēriski simetriski sadalīts lādiņš q bumbiņas centrā, tāds pats kā uz tās virsmas un vienāds ar φ 1 = q/4 πε 0 R; potenciāls, ko tajā pašā punktā rada punktveida lādiņš -2 q atrodas ārpus sfēras 2 attālumā R no tā centra ir φ 2 = – 2 q/4 πε 0 2 R; potenciāls bumbas centrā ir divu lauku superpozīcijas rezultāts, t.i. φ = φ 1 + φ 2 = q/4 πε 0 R–2 q/4 πε 0 2 R= 0 .
Darot testa priekšmeti ir ērti, lai ieraksts būtu pēc iespējas īsāks. Piemēram, šajā gadījumā pietiek ar vienu vispārīgu vienādojumu φ = q/4 πε 0 r.
Jo punktveida negatīvs lādiņš ir divreiz lielāks par lādiņu, kas sadalīts uz sfēras un atrodas divreiz tālāk no sfēras centra, no uzrakstītā vienādojuma var redzēt, ka abu lādiņu potenciāli ir vienādi pēc lieluma un pretēji pēc zīmes, tāpēc iegūtais potenciāls ir 0.
2 (CT 2001 Test 11. A 19).
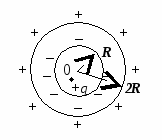 Iekšā sfērisks metāla slānis, kura iekšējais un ārējais rādiuss ir attiecīgi vienādi R
un 2
R
,
uz attālumu R/
2
q
.
Potenciāls sfēras centrā ir...
Iekšā sfērisks metāla slānis, kura iekšējais un ārējais rādiuss ir attiecīgi vienādi R
un 2
R
,
uz attālumu R/
2
q
.
Potenciāls sfēras centrā ir...
Risinājums
Grūtības izraisa lādiņu sadalījuma attēla konstruēšanu uz sfēriskā slāņa virsmām.
Elektrostatiskās indukcijas dēļ uz sfēras iekšējās virsmas parādās lādiņš –
q
, un ārpusē + q
.
Potenciāls sfēras centrā 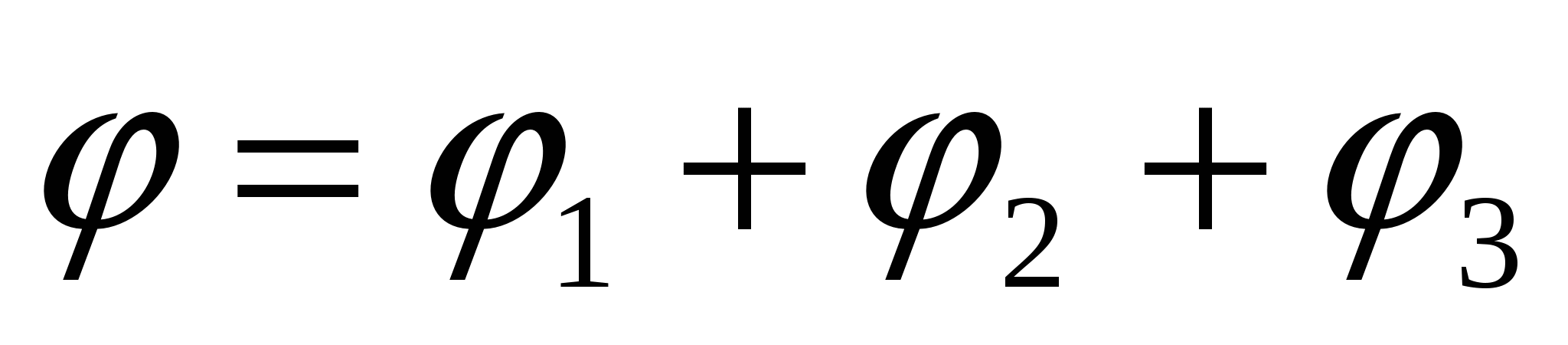 ;
;
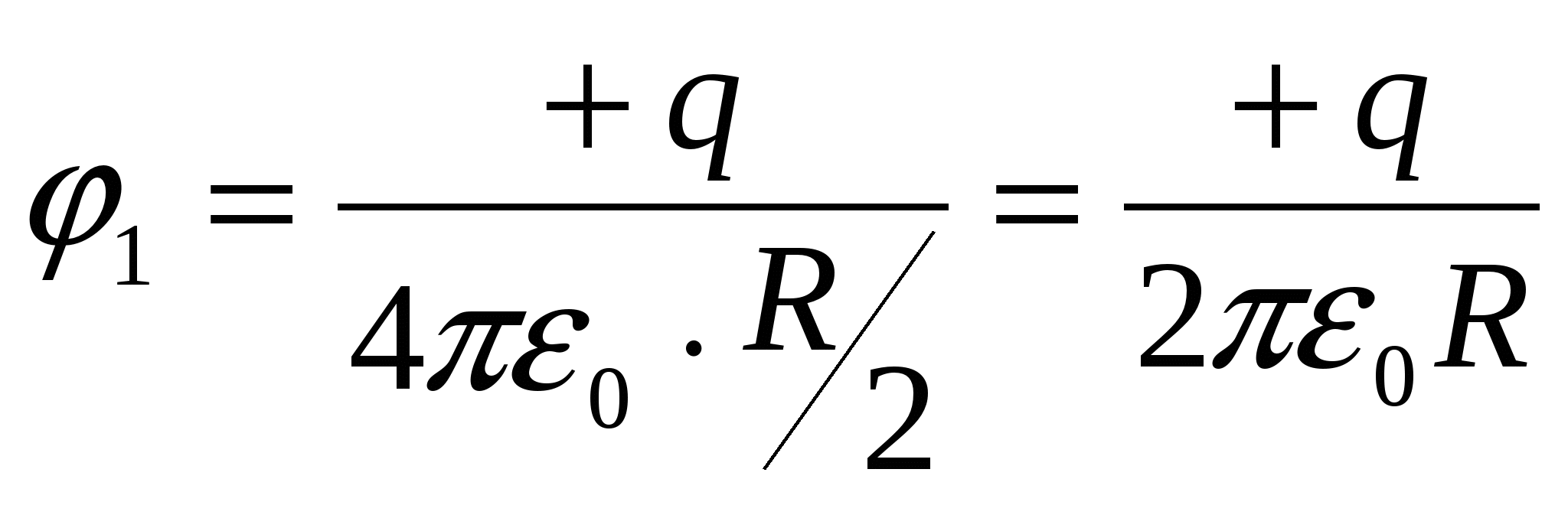 ;
; 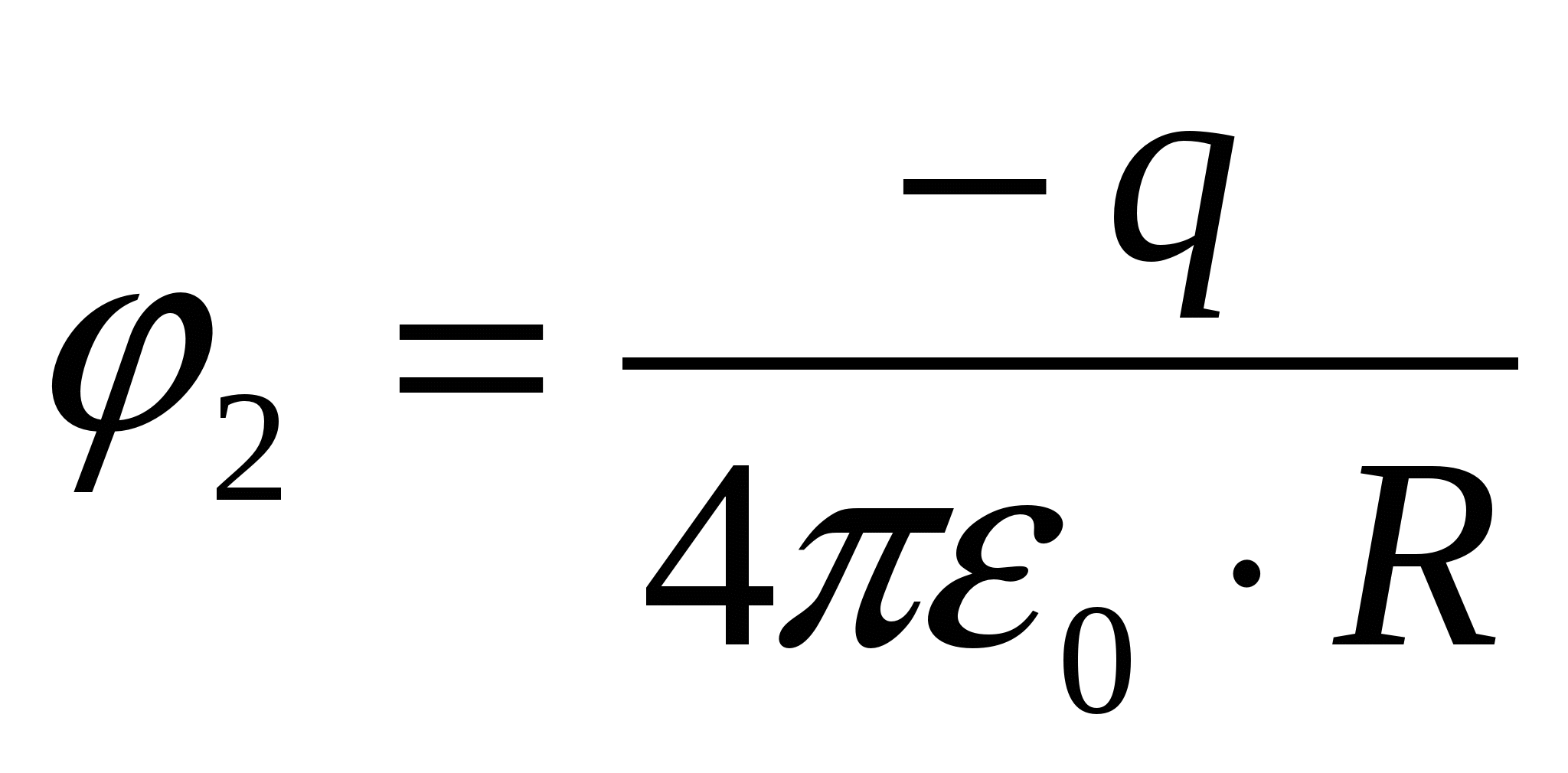 ;
; 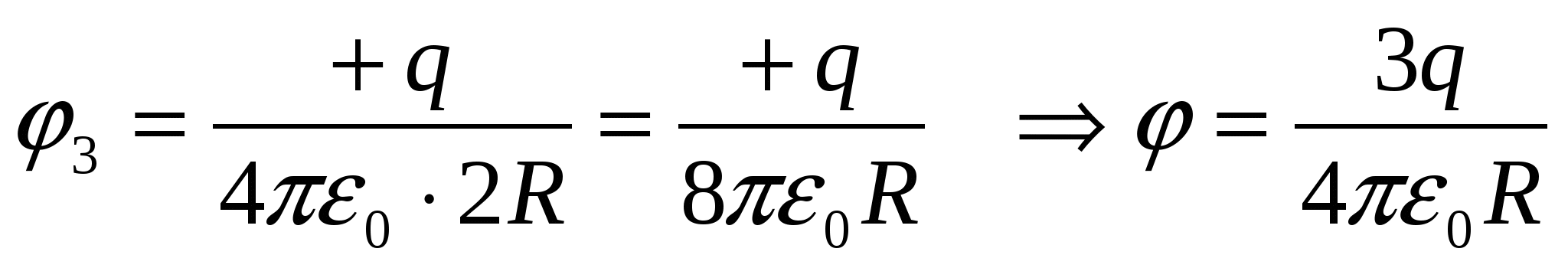 – atbilde 1.
– atbilde 1.
Līdzīgs uzdevums - A 19 ieskaitē Nr.12, 2001.g. :
Sfēriskā metāla slāņa iekšpusē, kura iekšējais un ārējais rādiuss ir attiecīgi vienāds ar 2 R un 4 R , uz attālumu R no centra ir punktveida pozitīvs lādiņš q . Potenciāls sfēras centrā ir ….
Atbilde: 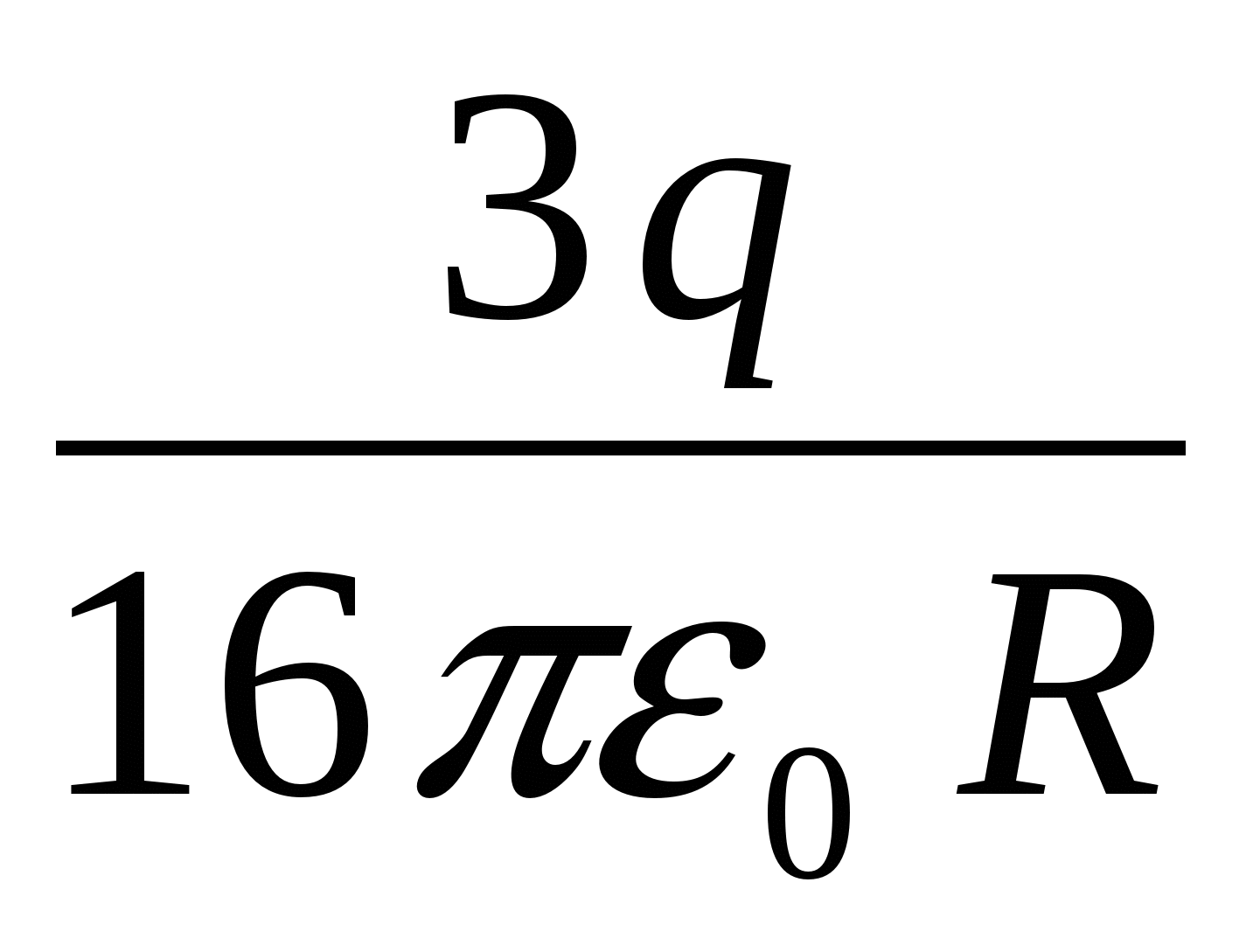
3 (CT 2000 tests ... A19). Metāla bumbiņa ar rādiusu R 1 kam ir potenciāls φ 1 , ko ieskauj neuzlādēts sfērisks vadošs apvalks ar rādiusu R 2 . Vai atrast bumbiņas potenciālu pēc tam, kad tā kādu laiku ir bijusi savienota ar apvalku?
Risinājums
Uzlādētās bumbas potenciāls 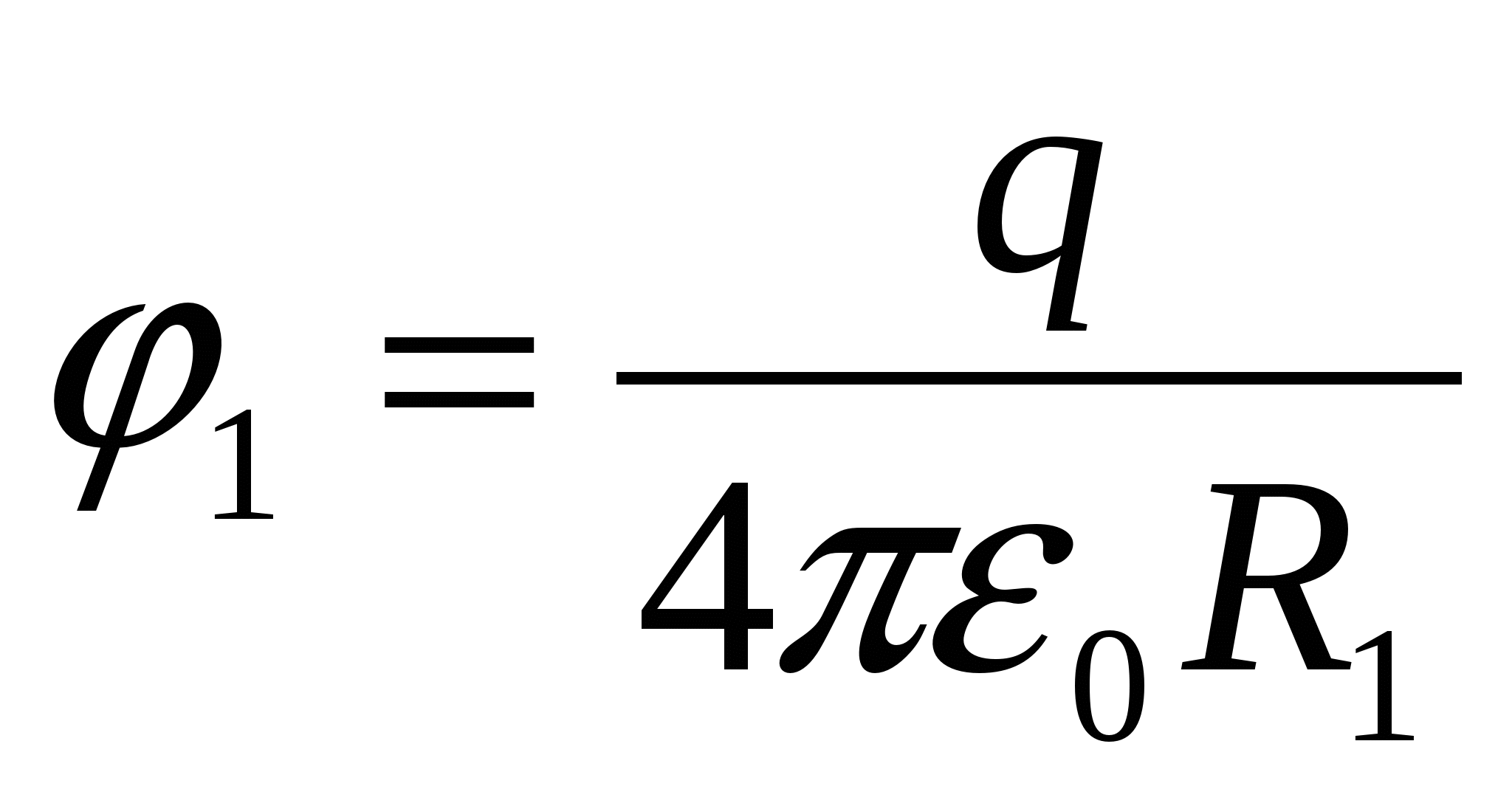 .
.
Ja uzlādēta bumba pieskaras čaulas iekšējai virsmai, lādiņi, cenšoties nosēsties uz iespējamo lielos attālumos viens no otra, dodieties uz čaulu. Lauka stiprums čaulas iekšpusē kļūst vienāds ar 0, lauka potenciāls čaulas punktos un iekšpusē ir vienāds ar 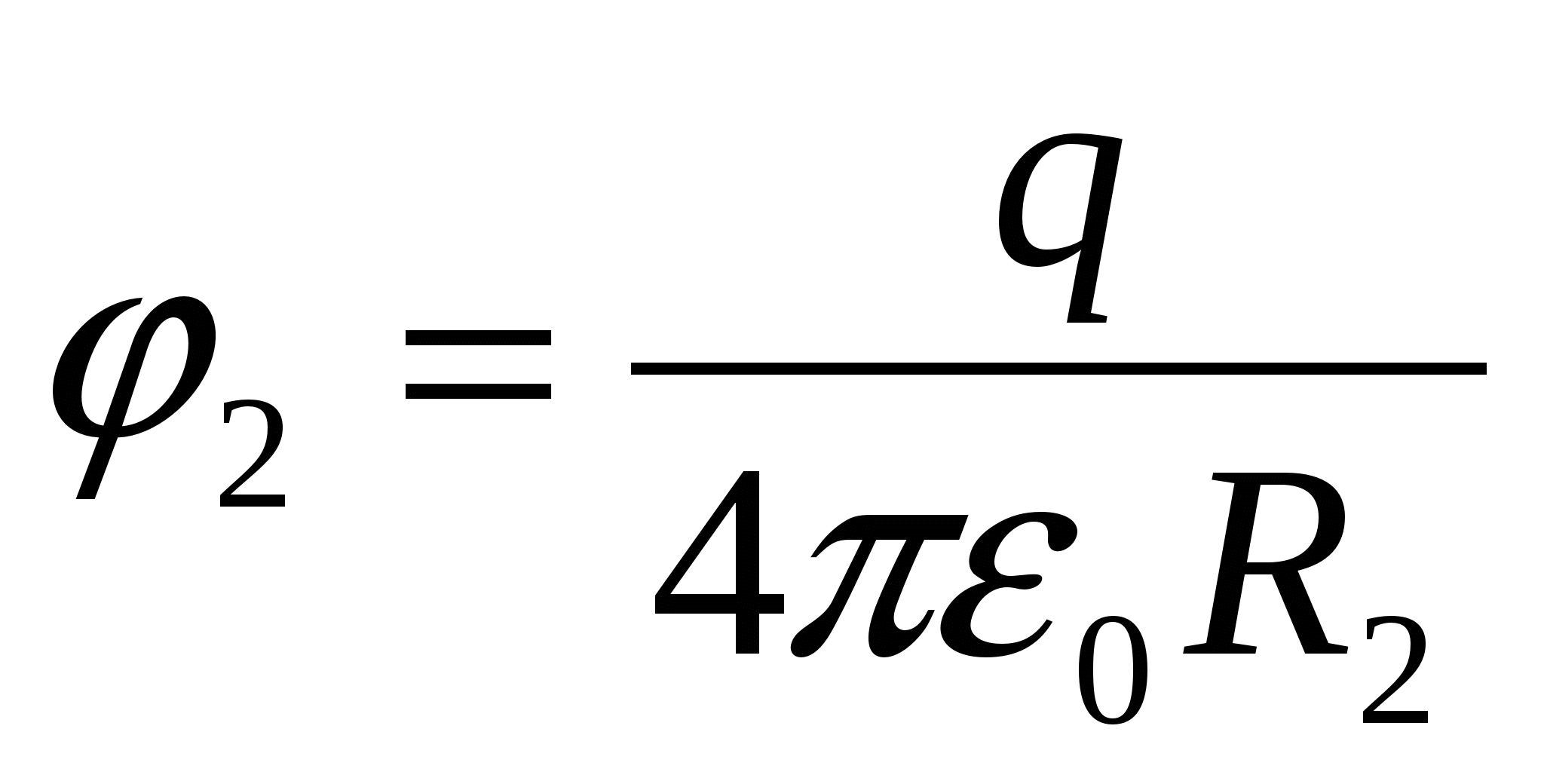 (bet ne 0! Skatīt iepriekšējo problēmu), kur
(bet ne 0! Skatīt iepriekšējo problēmu), kur  . Tādējādi čaulas un tajā esošās un ar to savienotās bumbiņas potenciāls ir vienāds ar
. Tādējādi čaulas un tajā esošās un ar to savienotās bumbiņas potenciāls ir vienāds ar 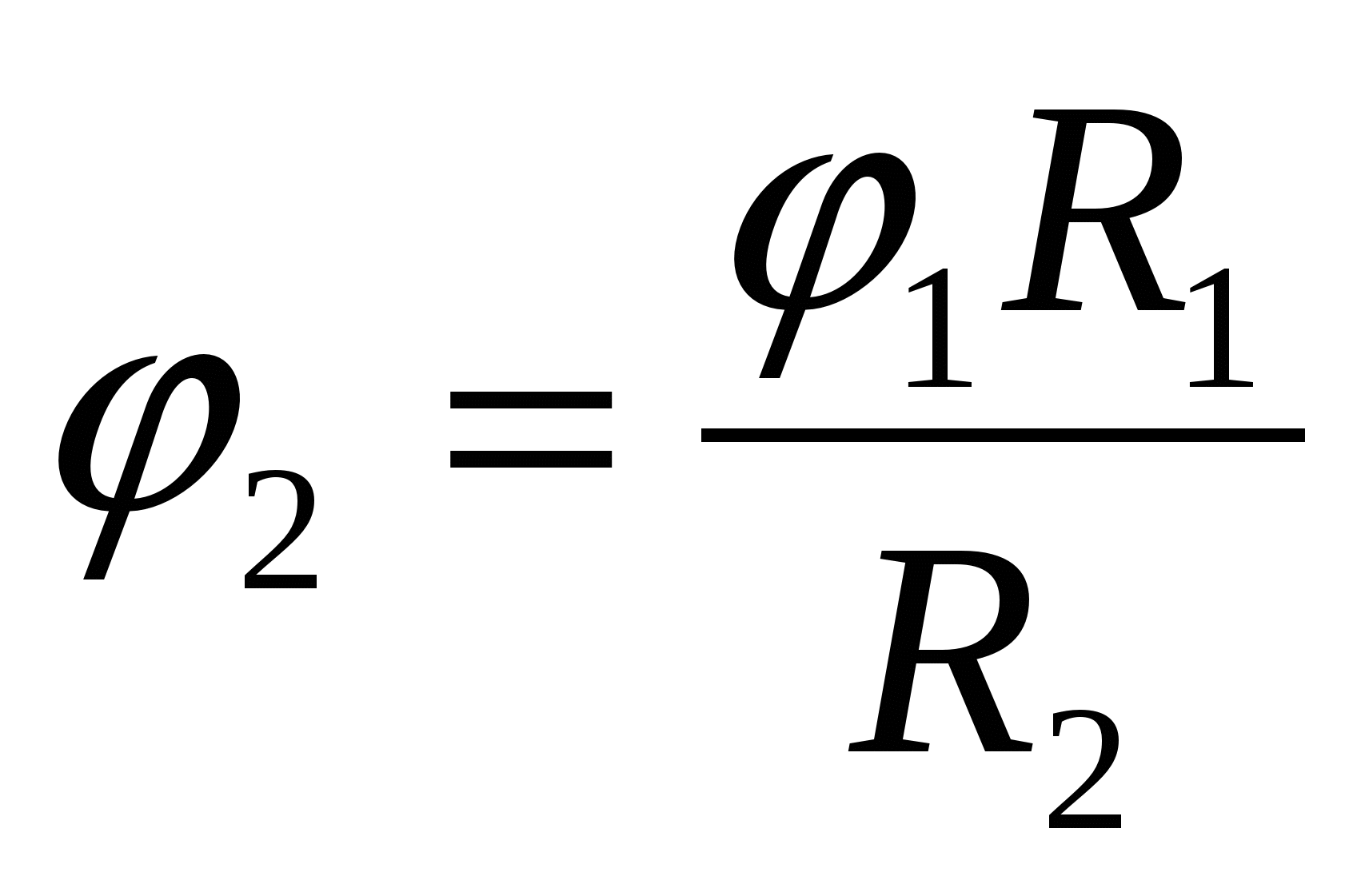 – atbildi.
– atbildi.
Pa labi atbilde -1.
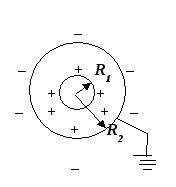
4 (CT 2000 tests ... A19). Metāla lodītes rādiuss R 1 kam ir potenciāls φ 1 , ko ieskauj sfērisks vadošs apvalks ar rādiusu R 2 . Kāds būs bumbas potenciāls, ja čaula ir iezemēta?
Risinājums
Visbiežāk kļūda ir tas, ka netiek ņemts vērā lauka potenciāls, ko rada lādiņi, kas inducēti uz apvalka, kad tas ir iezemēts.
Pirmais variants risinājumus. Potenciāls uz bumbas virsmas, ko rada bumbas lādiņš 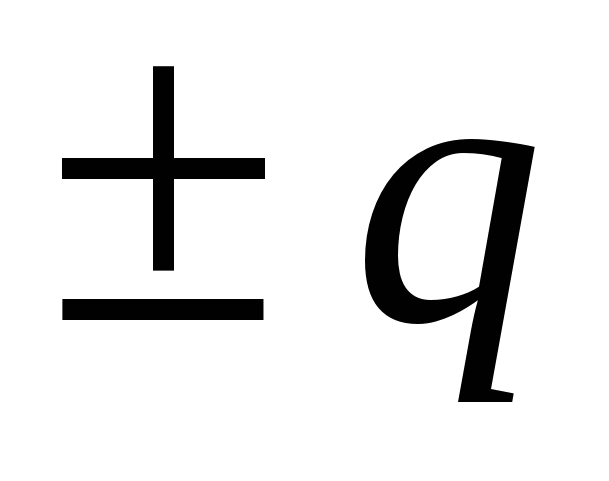 , ir vienāds ar
, ir vienāds ar 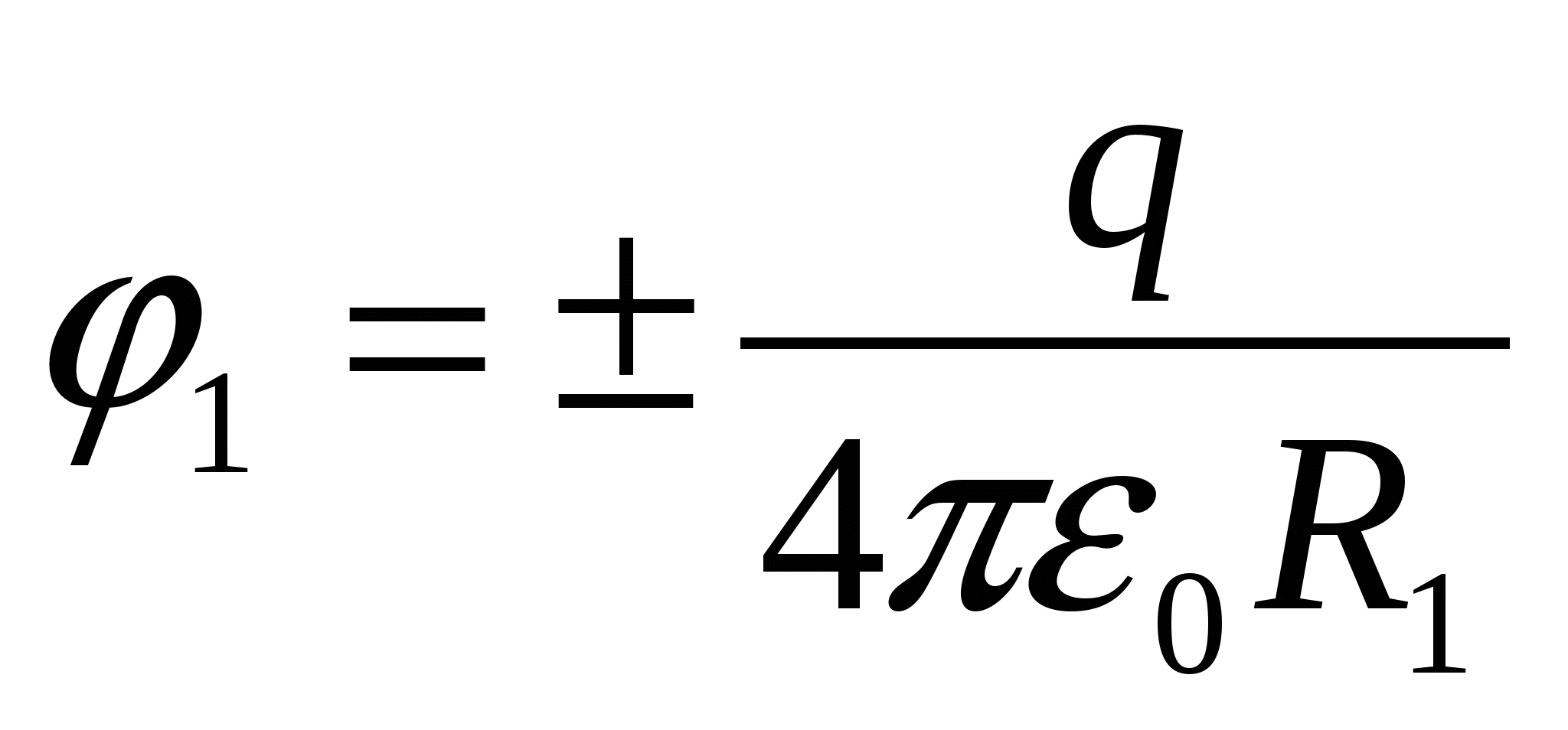 . Pēc tam, kad apvalks ir iezemēts, uz tā parādās inducēts lādiņš
. Pēc tam, kad apvalks ir iezemēts, uz tā parādās inducēts lādiņš 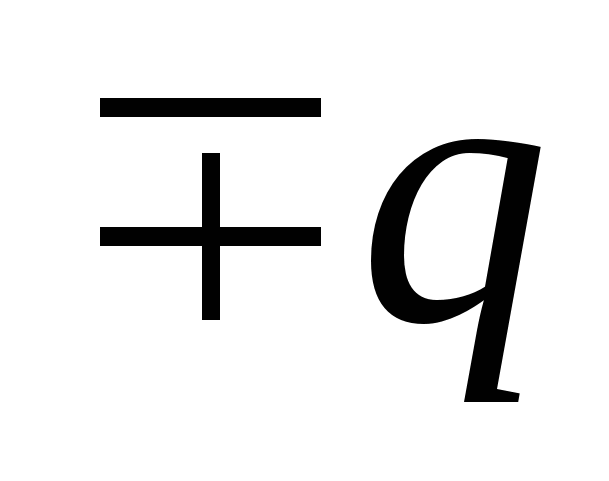 , kas uz čaulas un tā iekšpusē rada potenciālu
, kas uz čaulas un tā iekšpusē rada potenciālu 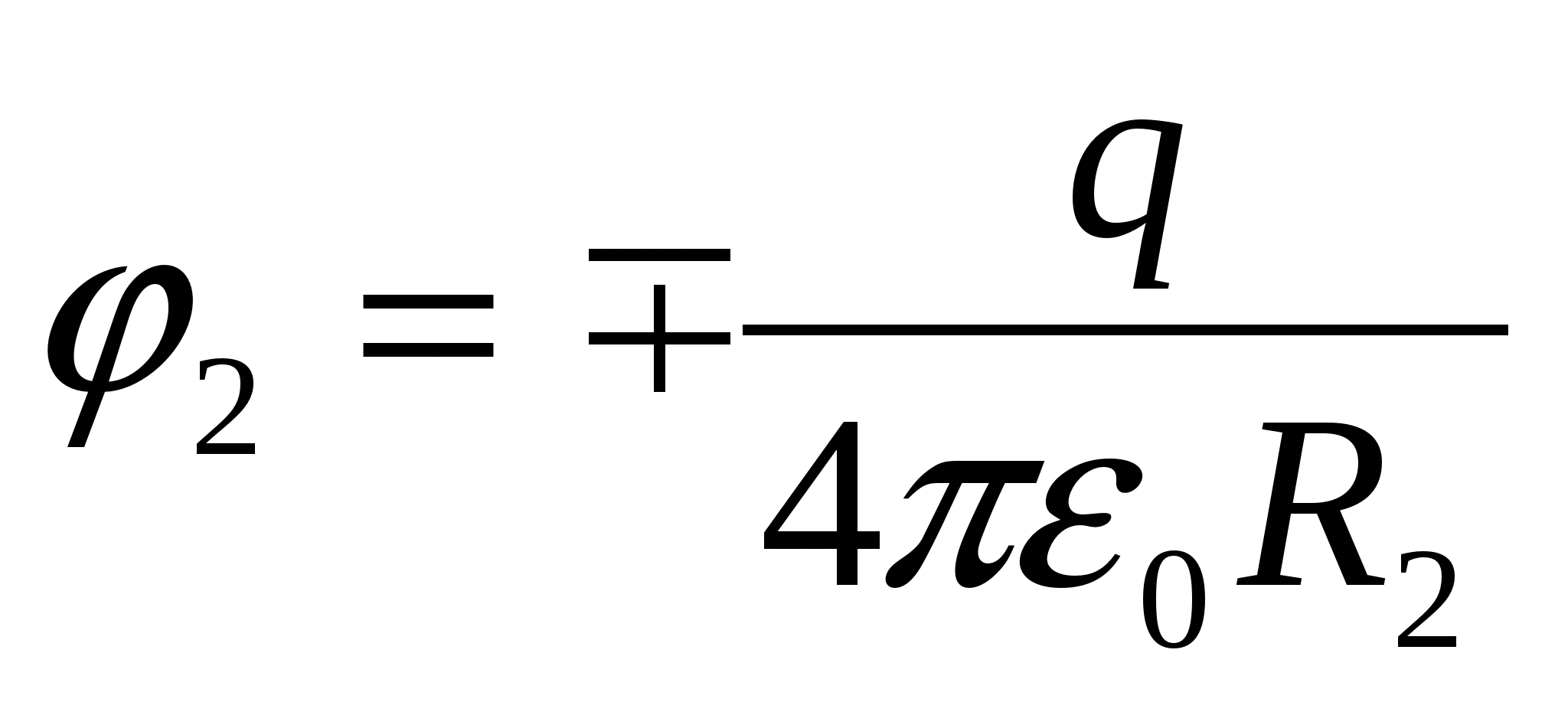 .
.
Bumbiņas sākotnējā lauka un čaulas inducētā lādiņa radītā lauka superpozīcija dod potenciālu uz bumbas virsmas
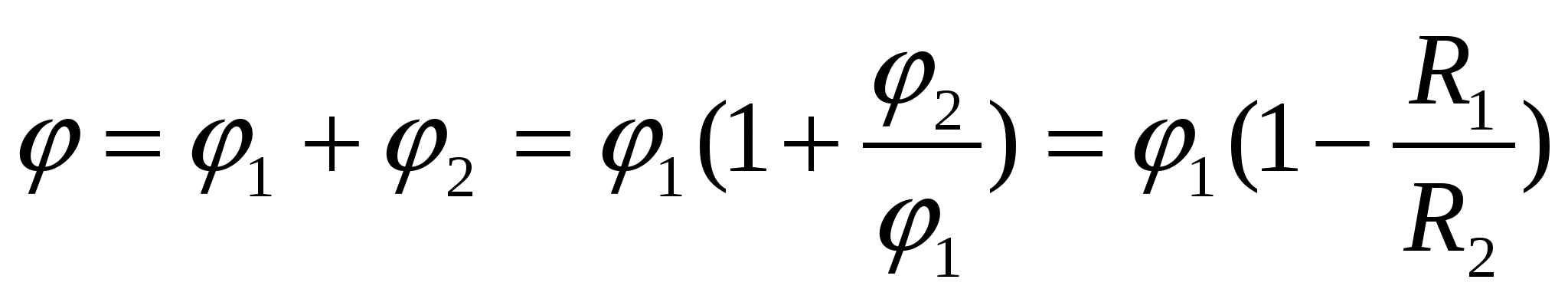 – atbildi.
– atbildi.
Otrais variants risinājumus. Var apgalvot, ka apvalka potenciāls pēc zemēšanas ir 0, kā tas ir ierasts tehnoloģijā (par potenciālās enerģijas atskaites punktu tiek ņemts iezemēts apvalks), no šī stāvokļa tiek atrasts inducētā lādiņa lielums un zīme. Apvalka potenciāls φ 2 ir potenciāla summa, ko rada uz tā izraisītais lādiņš q 2 un bumbas lauka potenciāls φ 1 :
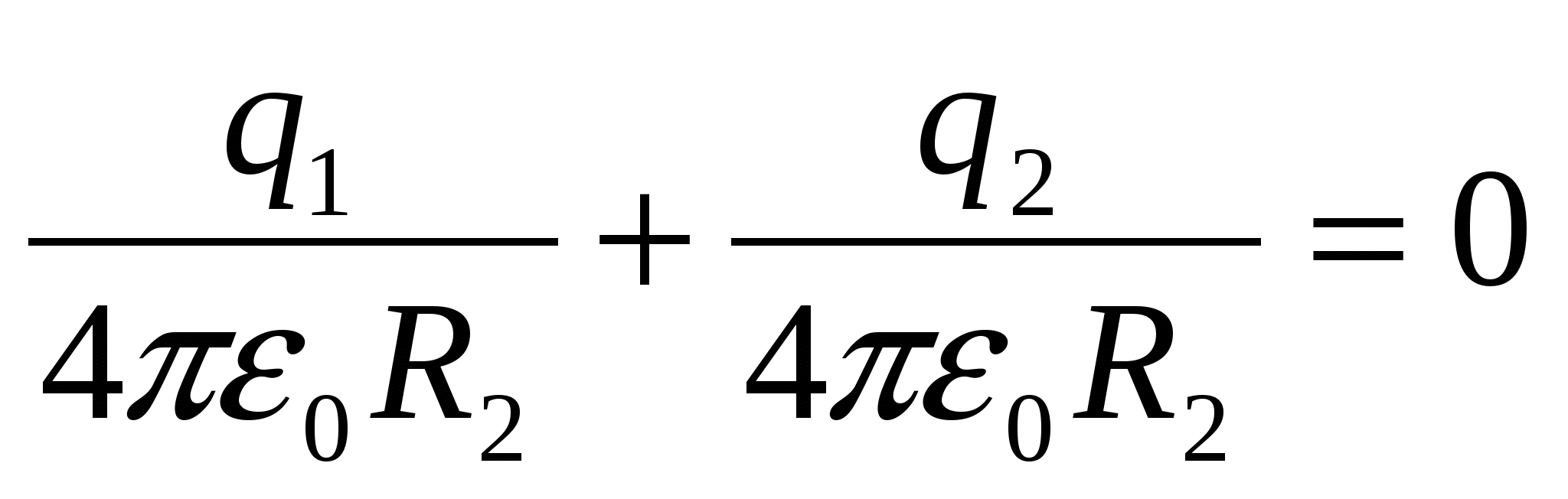 ,
,  q 1
= –
q 2.
.
q 1
= –
q 2.
.
Mēs atrodam bumbas potenciālu pēc tam, kad apvalks ir iezemēts:
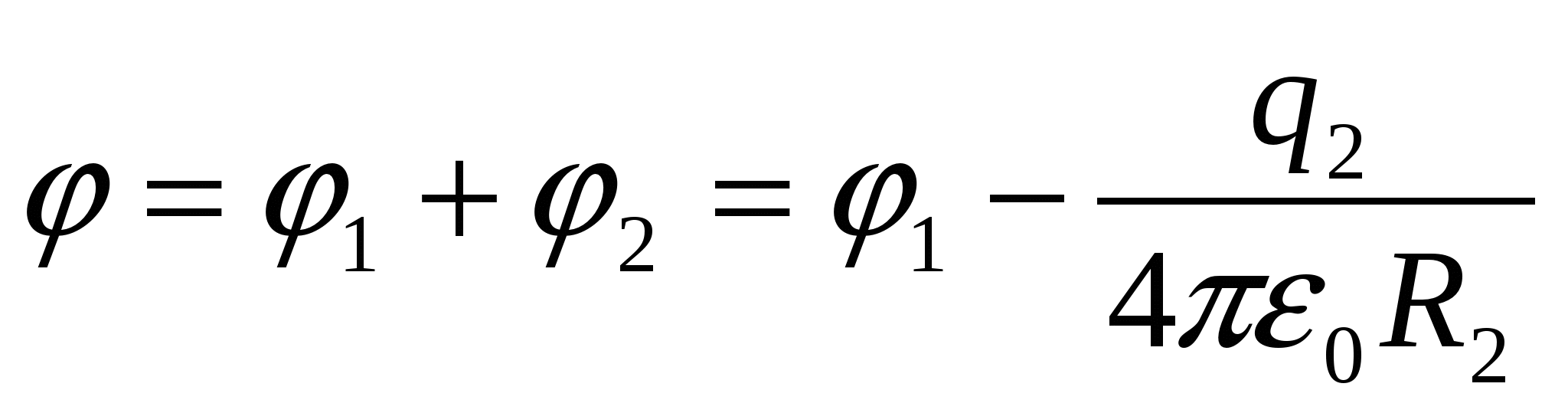 (1).
(1).
No 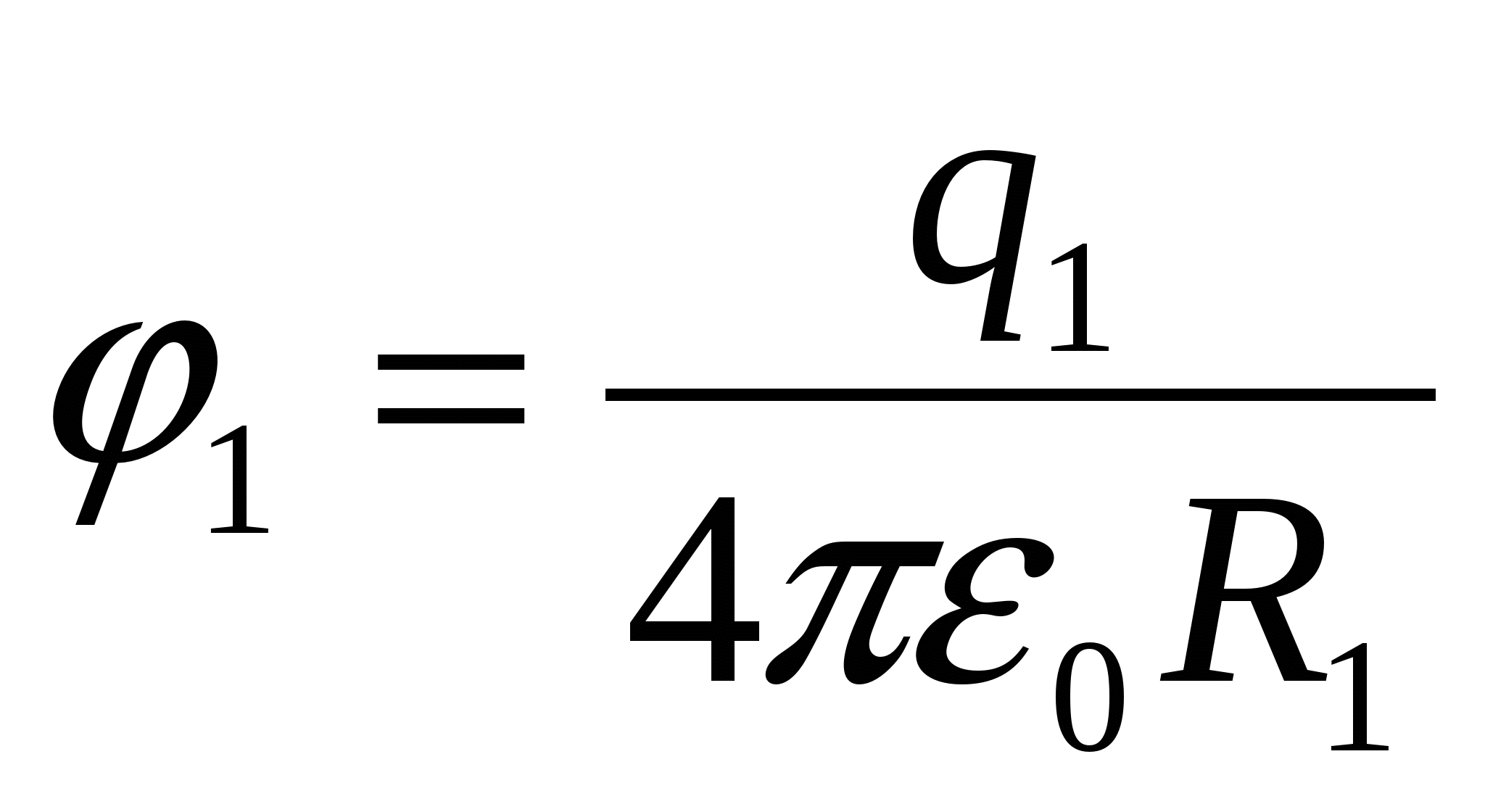 atrast
atrast 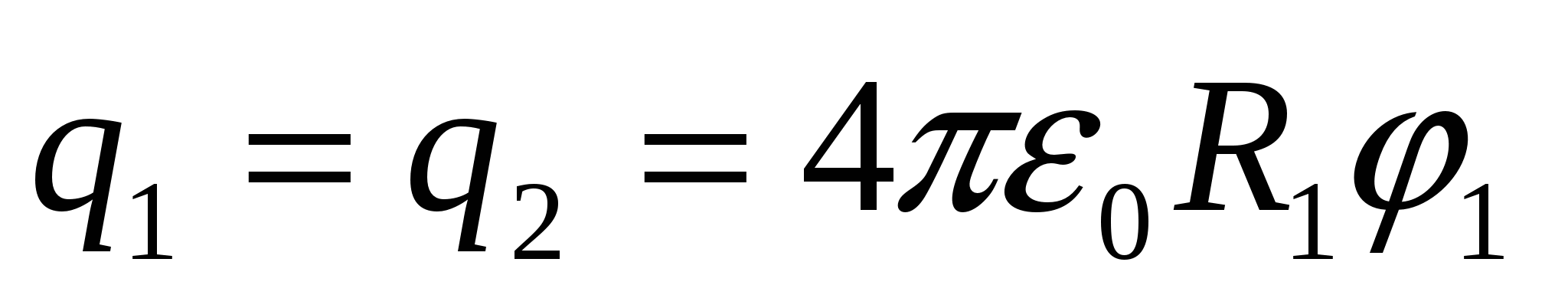 , mēs aizstājam ar (1), mēs iegūstam atbildi:
, mēs aizstājam ar (1), mēs iegūstam atbildi: 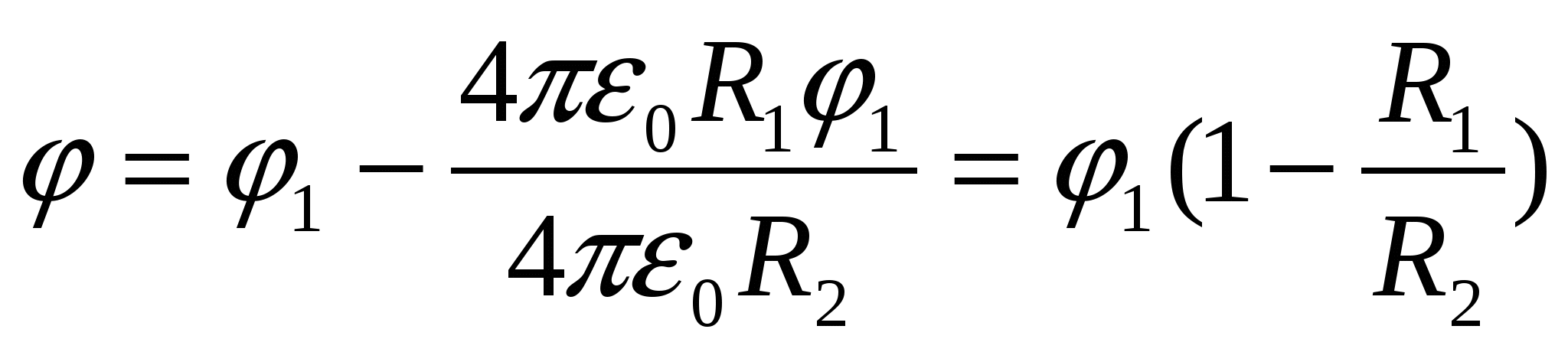 .
.
Šim risinājumam ir daži trūkumi:
– iepriekš atrisinātos uzdevumos potenciāls (potenciālā enerģija) tika skaitīts no punkta, kas ir bezgalīgi tālu no lādiņa, kam ir skaidra fiziska nozīme; ir loģiski vienmēr izmantot vienu un to pašu atskaites punktu;
- risinājums izrādījās apgrūtinošāks.
5
(CT 2001 Test 3. A19). Plāns fiksēta rādiusa gredzens R vienmērīgi uzlādēts, lai būtu maksa par gredzena garuma vienību + γ .
Vakuumā uz gredzena ass attālumā l no tā centra novieto nelielu bumbiņu ar lādiņu + q. Ja bumba tiek atbrīvota, tad kustības procesā tā iegūs maksimālo kinētisko enerģiju, kas vienāda ar
| 1) 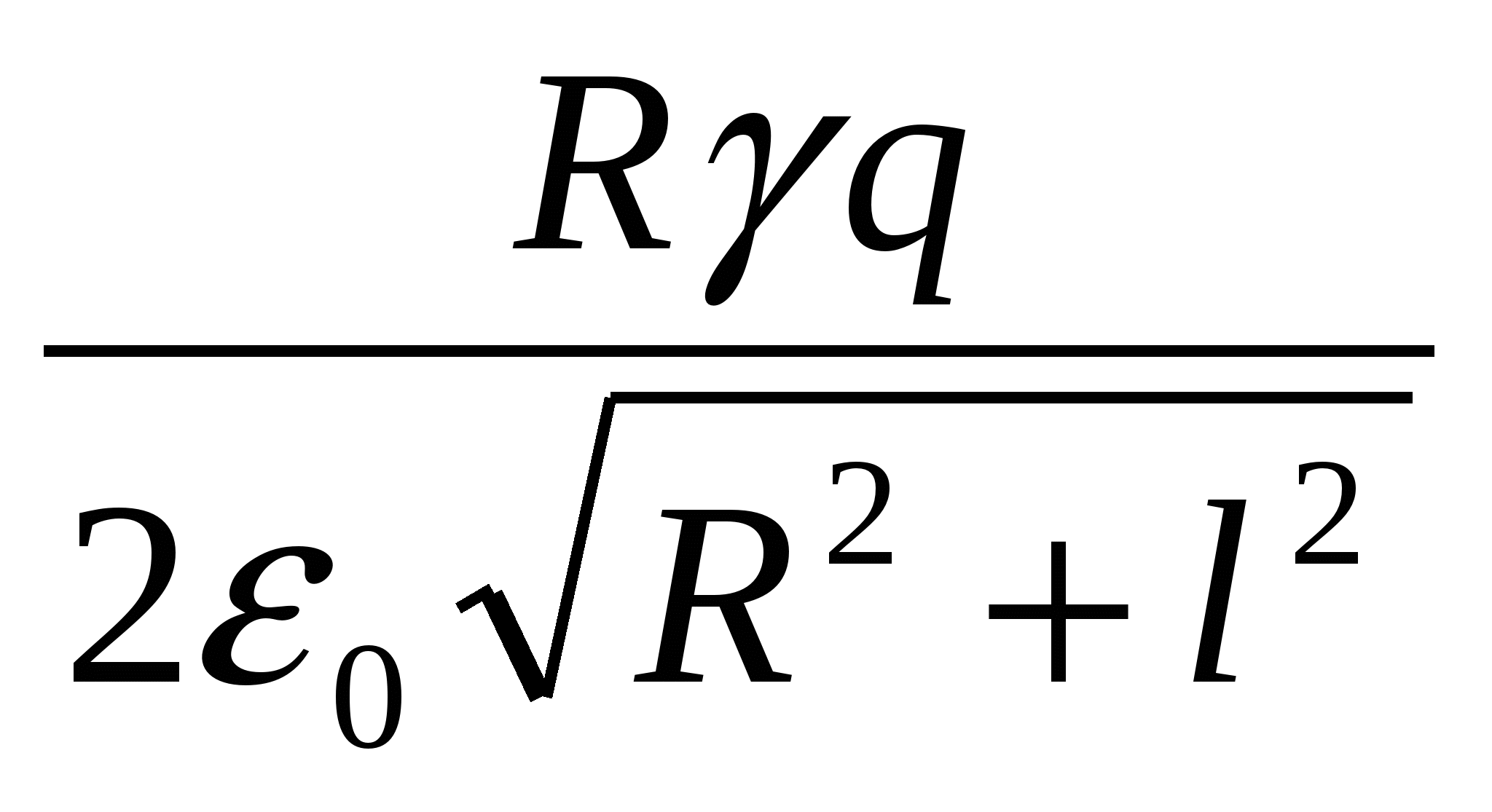 | 2) 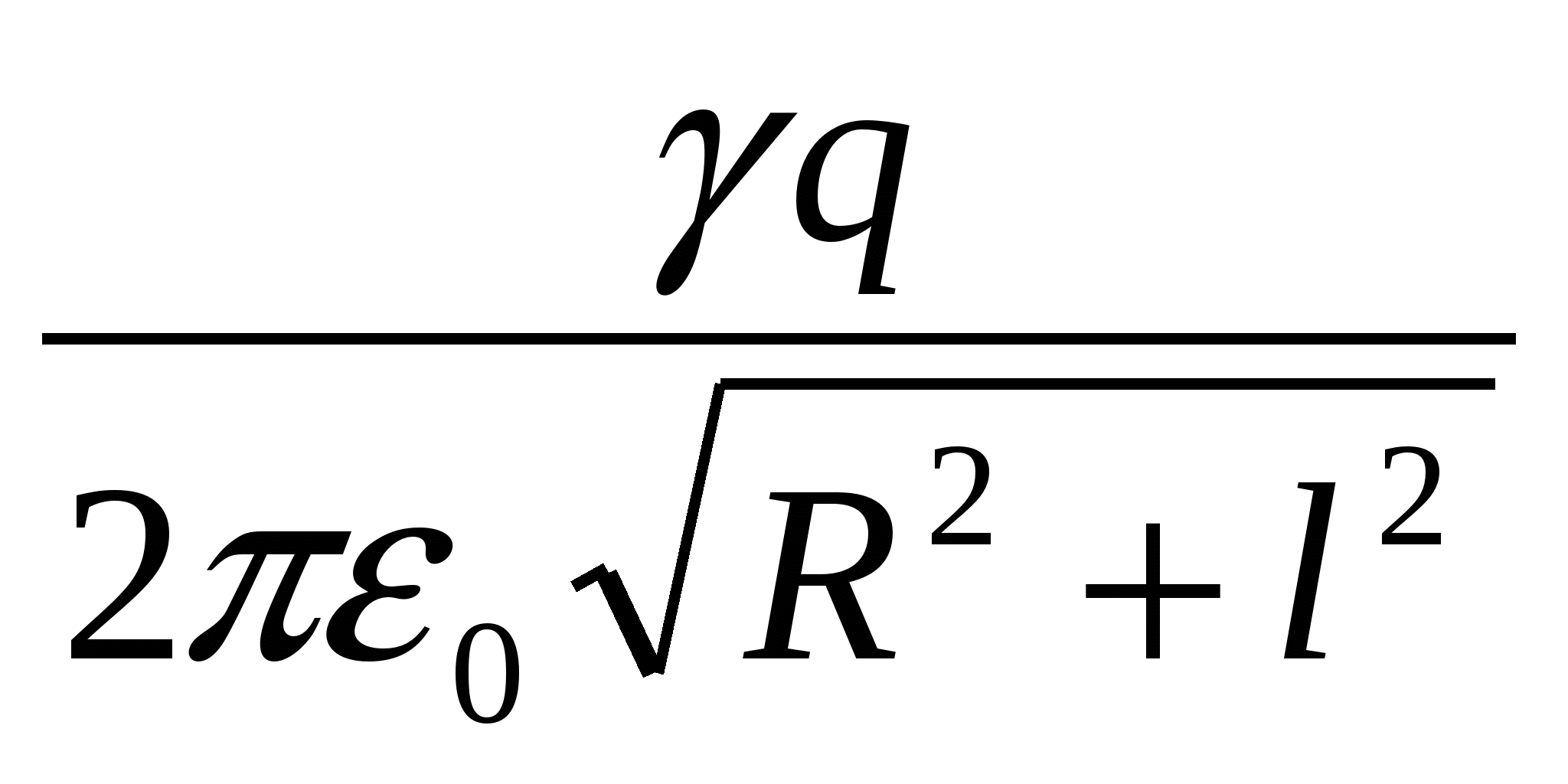 | 3) 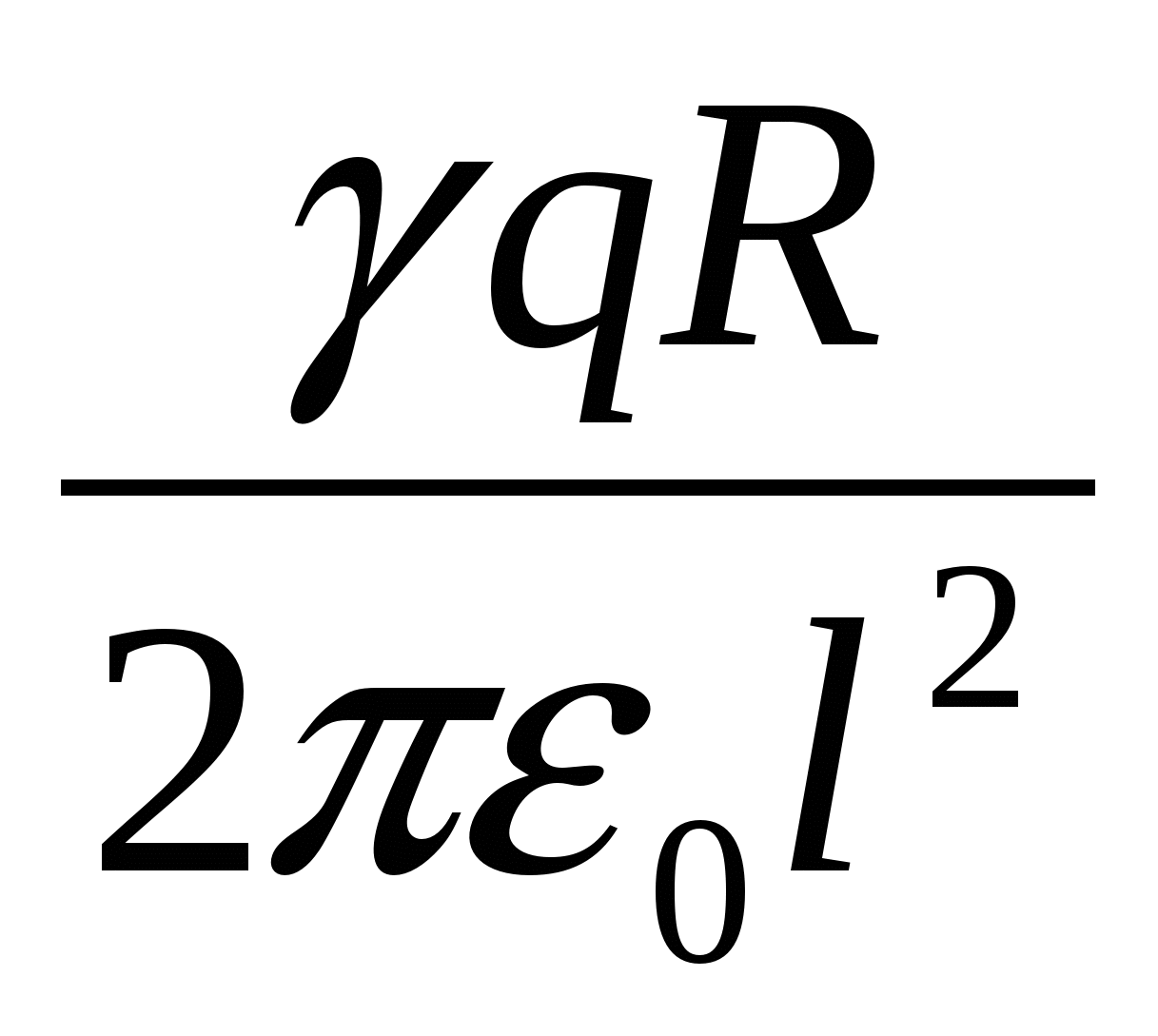 |
| 4) 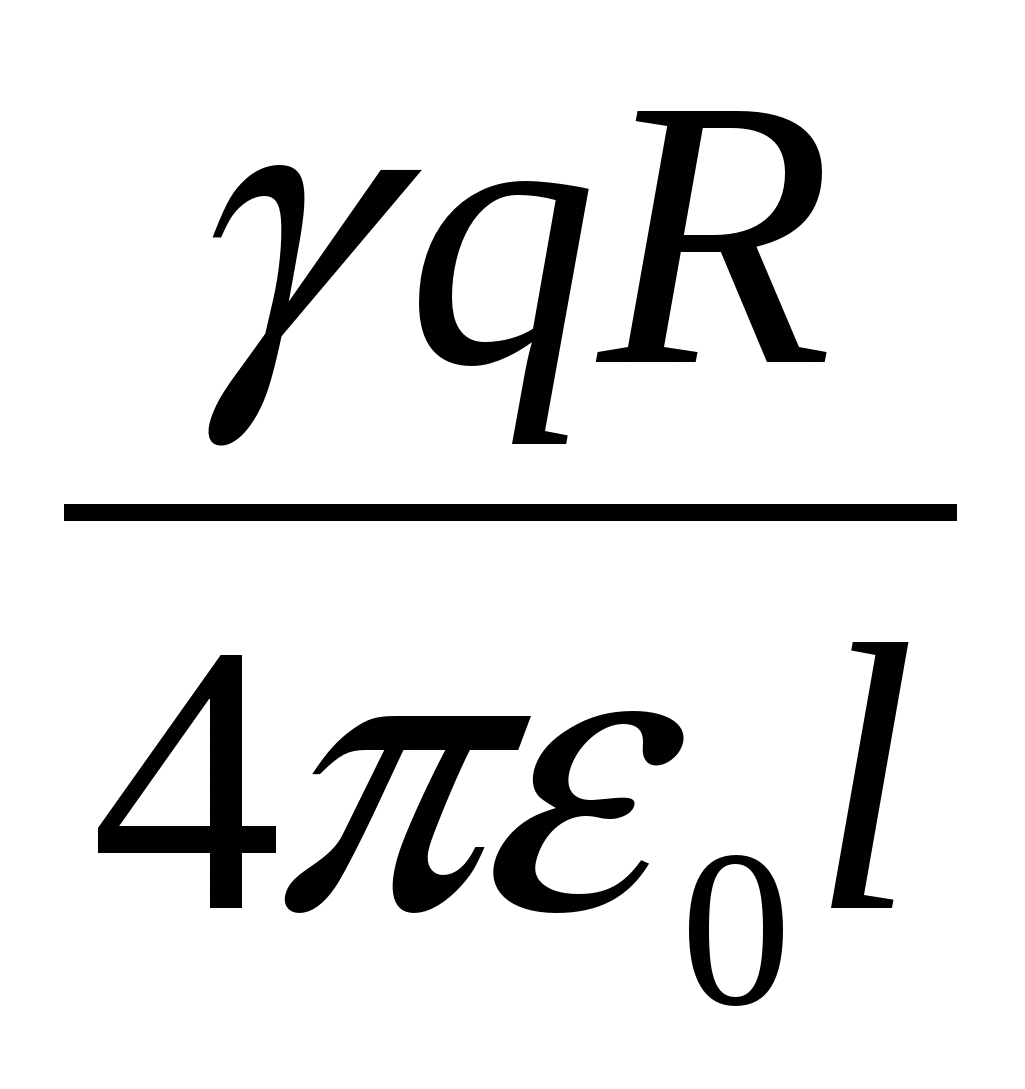 | 5) 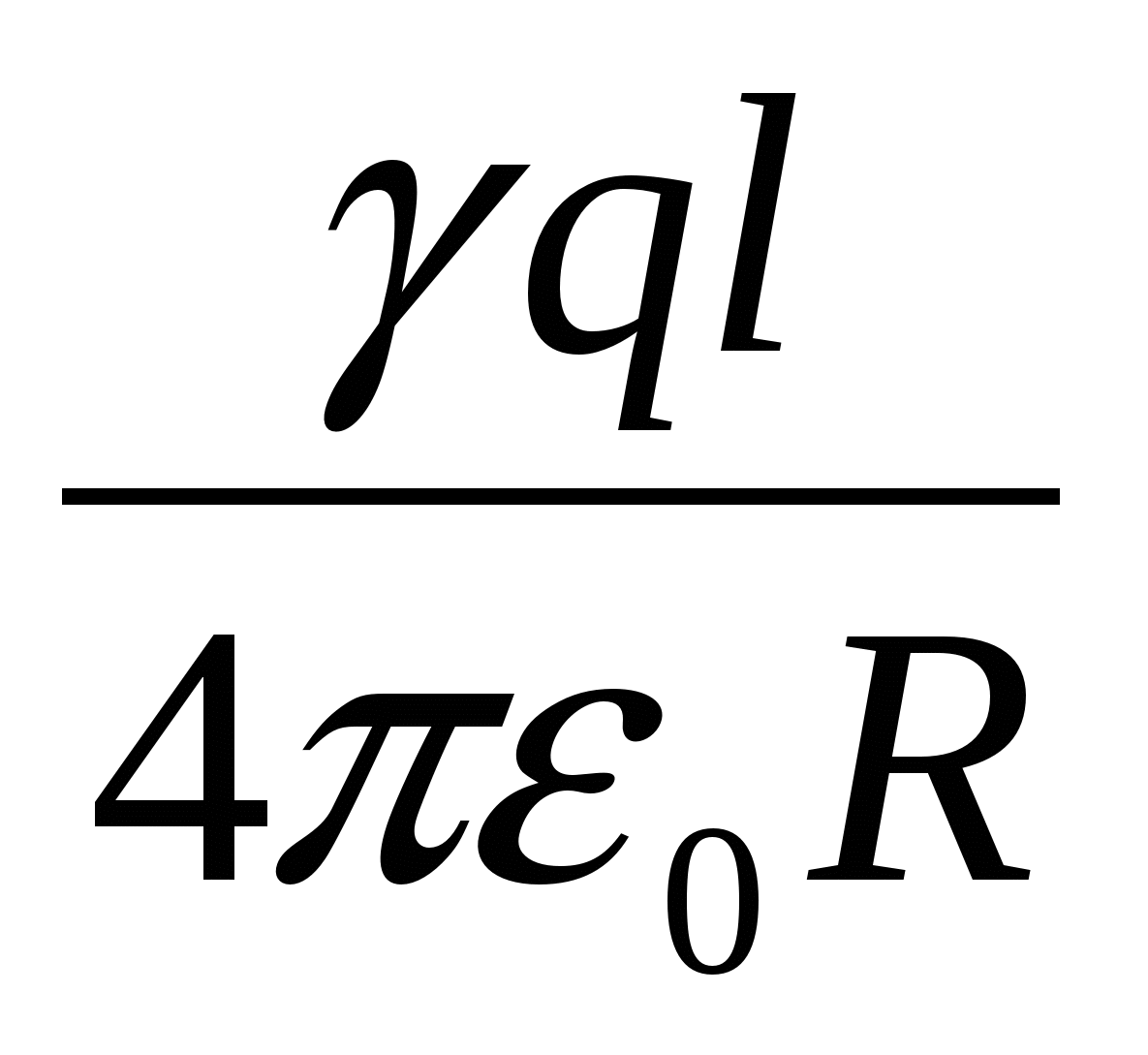 |
R 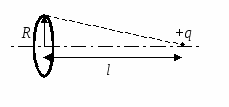 risinājums
risinājums
Saskaņā ar enerģijas nezūdamības likumu E = U, kur U- mijiedarbības enerģija punktu maksa un gredzeni.
Tipiska kļūda: risinot šo problēmu, tiek uzskatīts, ka, pateicoties lādiņa sadalījuma simetrijai gar gredzenu, ir iespējams to “izvilkt” uz gredzena centru un atrast gredzena radītā lauka potenciālu vietā lādiņa kā punktveida lādiņa lauka potenciālu: 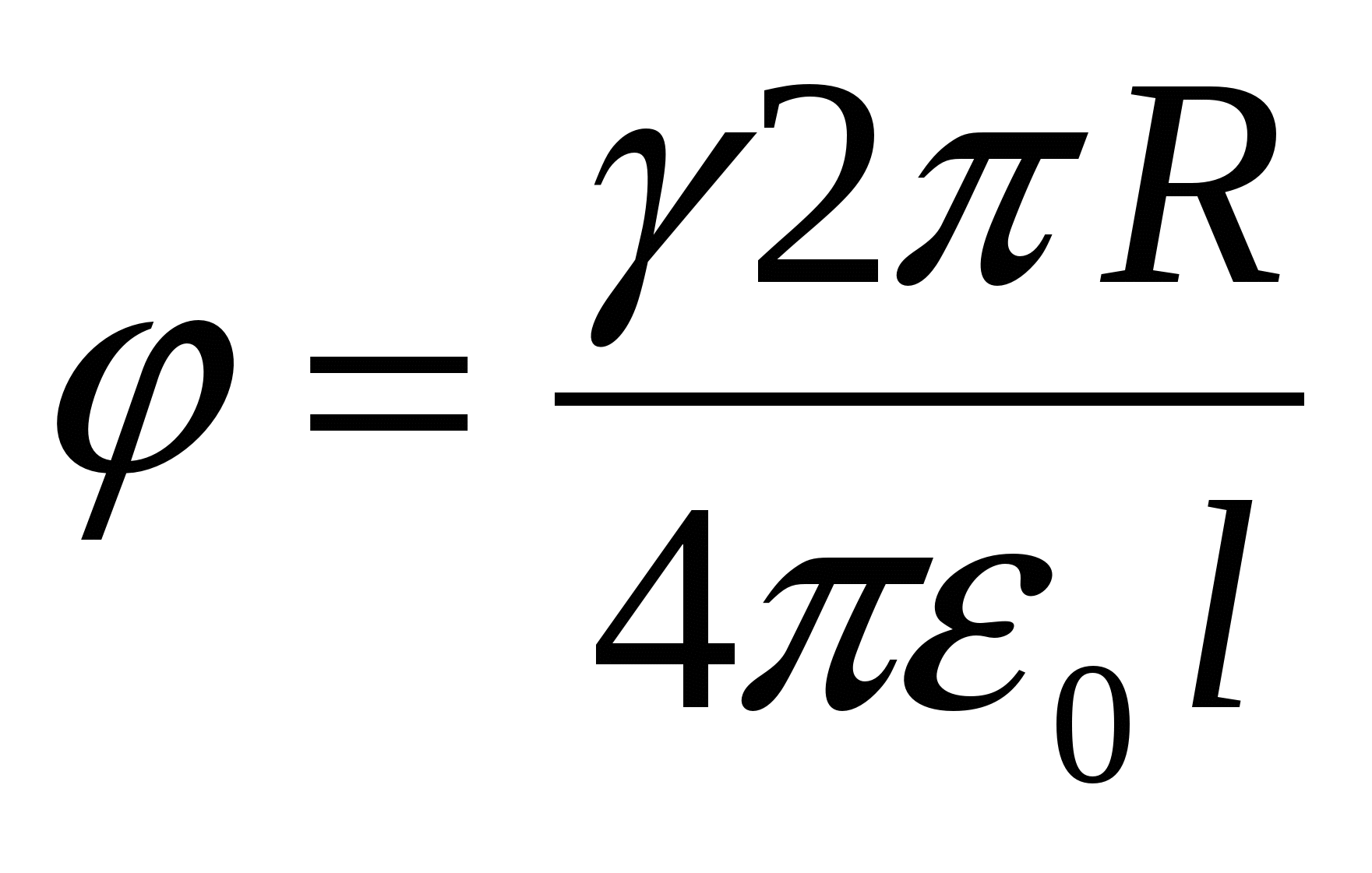 . Tomēr to nevar izdarīt, jo lādiņa simetrija nav telpiska, bet plakne. Patiesībā gredzenu vajadzētu sadalīt mazos elementos, ko var apsvērt materiālie punkti, nosaka katra šāda punktveida lādiņa lauka potenciālu lādiņa + vietā q
un summējiet rezultātus:
. Tomēr to nevar izdarīt, jo lādiņa simetrija nav telpiska, bet plakne. Patiesībā gredzenu vajadzētu sadalīt mazos elementos, ko var apsvērt materiālie punkti, nosaka katra šāda punktveida lādiņa lauka potenciālu lādiņa + vietā q
un summējiet rezultātus:
Gredzena mijiedarbības enerģija ar lādiņu un lādiņa maksimālā kinētiskā enerģija ir vienāda saskaņā ar enerģijas nezūdamības likumu: 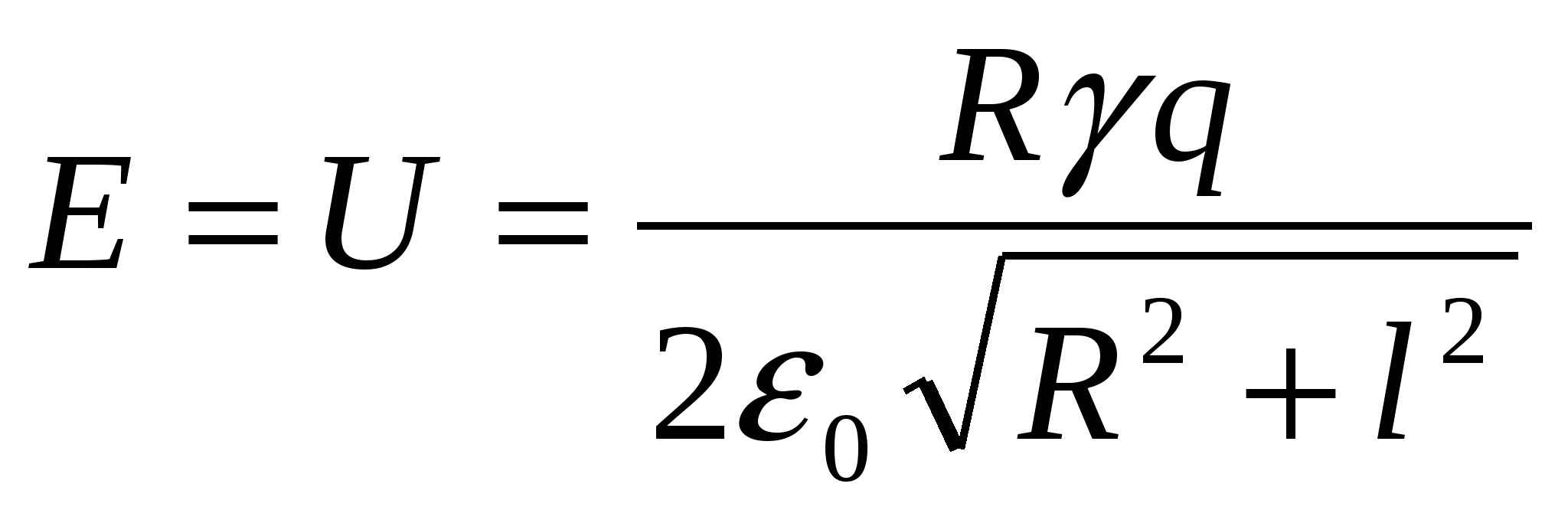 - atbildi.
- atbildi.
Līdzīgā veidā potenciāls tiek atrasts, risinot uzdevumu A 19 no TsT 2001 testa Nr. 8: 10–9 C lādiņš vienmērīgi tiek sadalīts pa tievu stieples gredzenu ar rādiusu 3 cm. Nosakiet potenciālo starpību starp gredzena centru un punktu, kas atrodas uz gredzena ass 4 cm attālumā no centra. Atbilde: 120 V.
6
(TsT 2000 Test 3. A 20).Ja metāla lodīte ar rādiusu R
1
, uzlādēts līdz potenciālam φ
1
, savienot plānas
stieple ar neuzlādētu metāla lodi ar rādiusu R
2, tad savienojuma kopējais potenciāls būs vienāds ar
| 1) 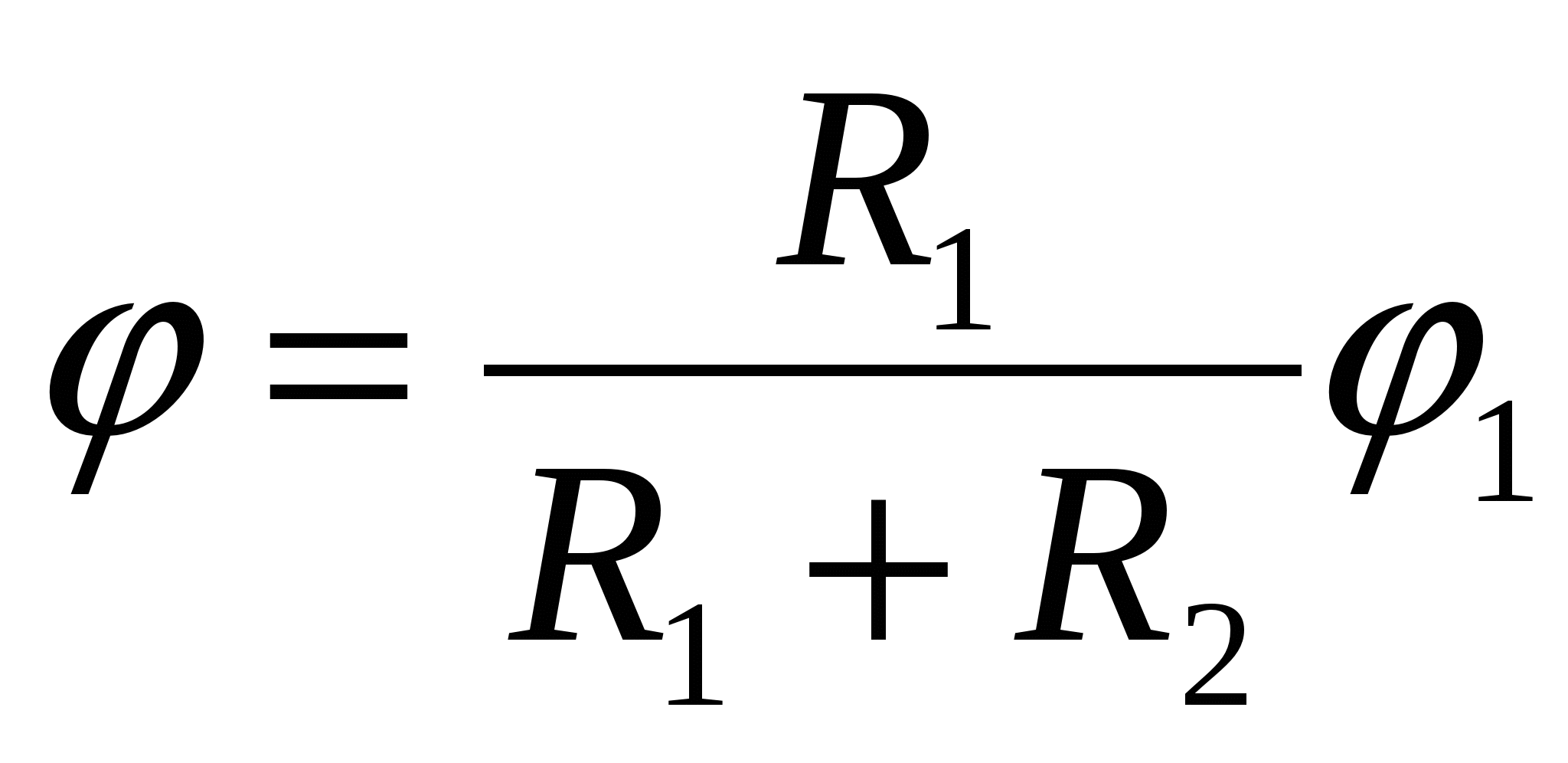 | 2) 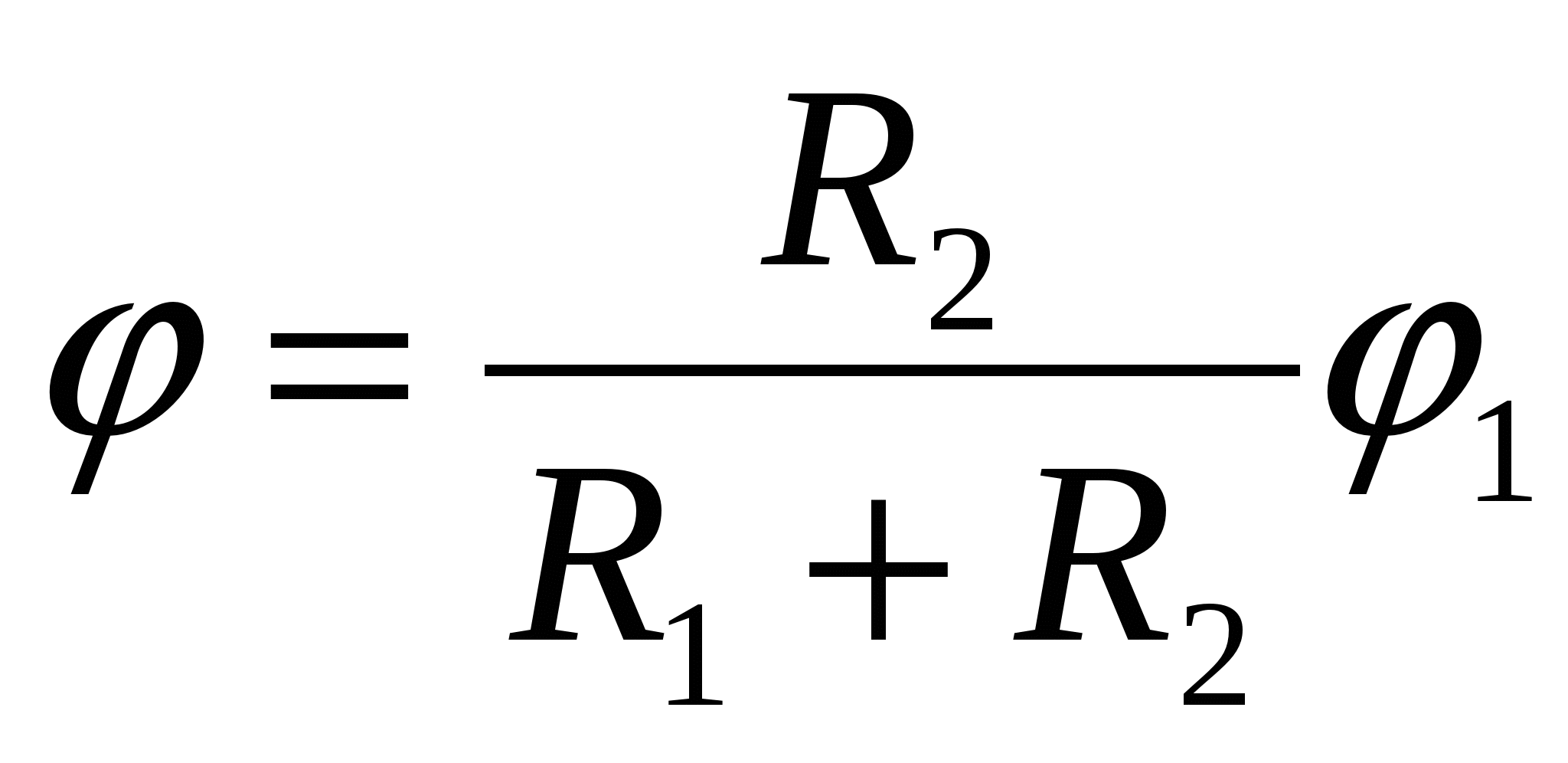 | 3) 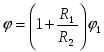 |
| 2) 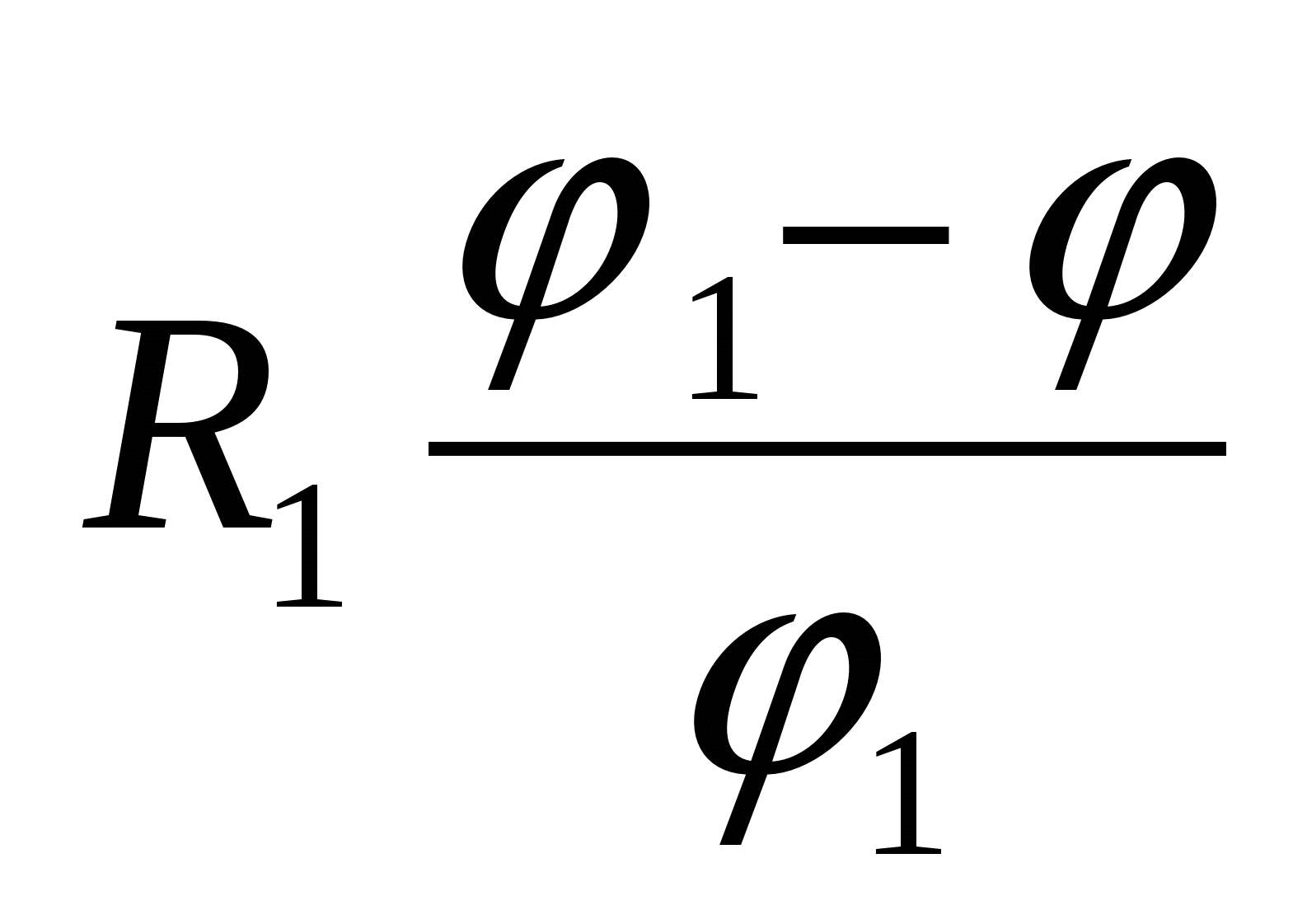 | 3) 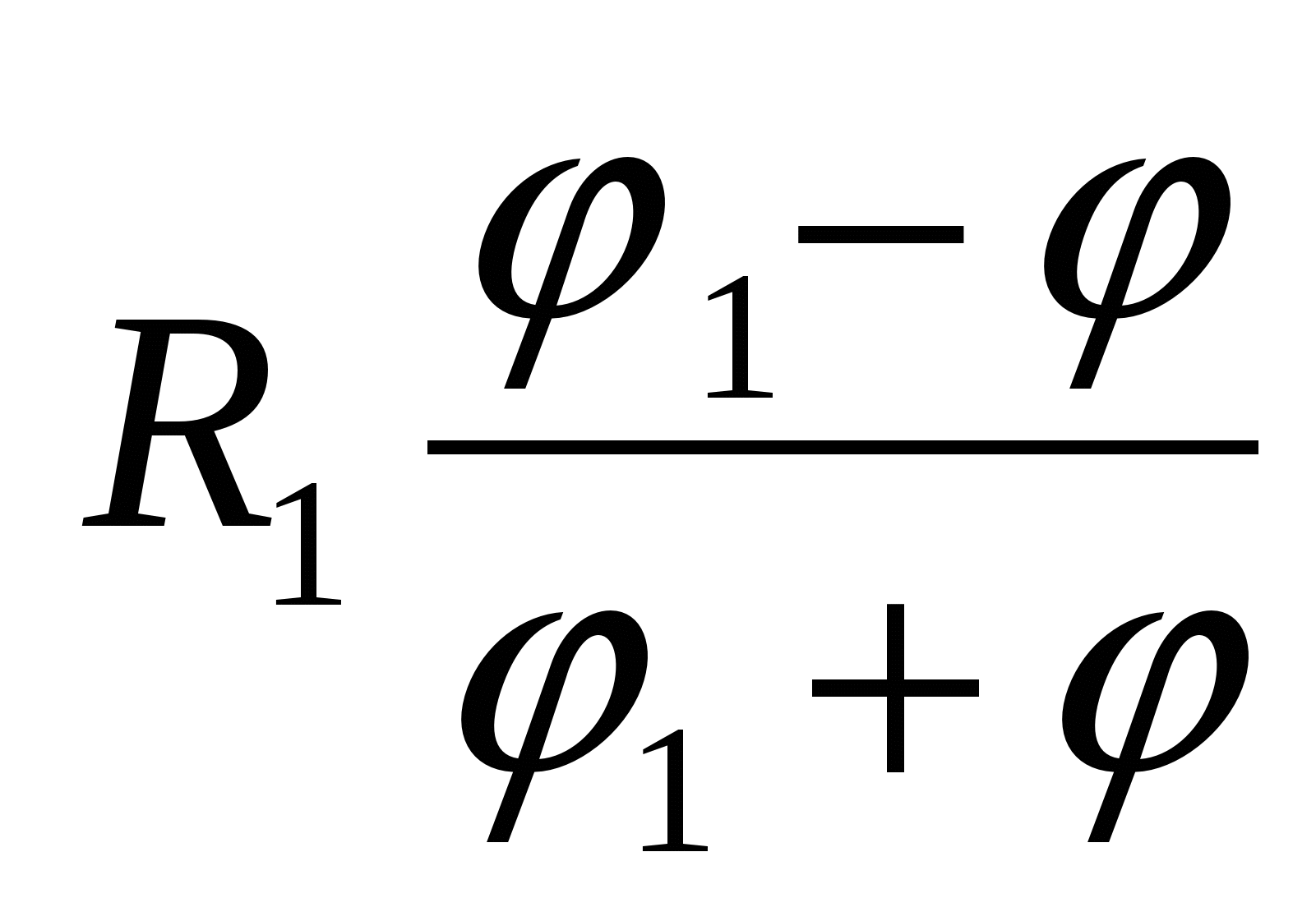 |
|
| 4) 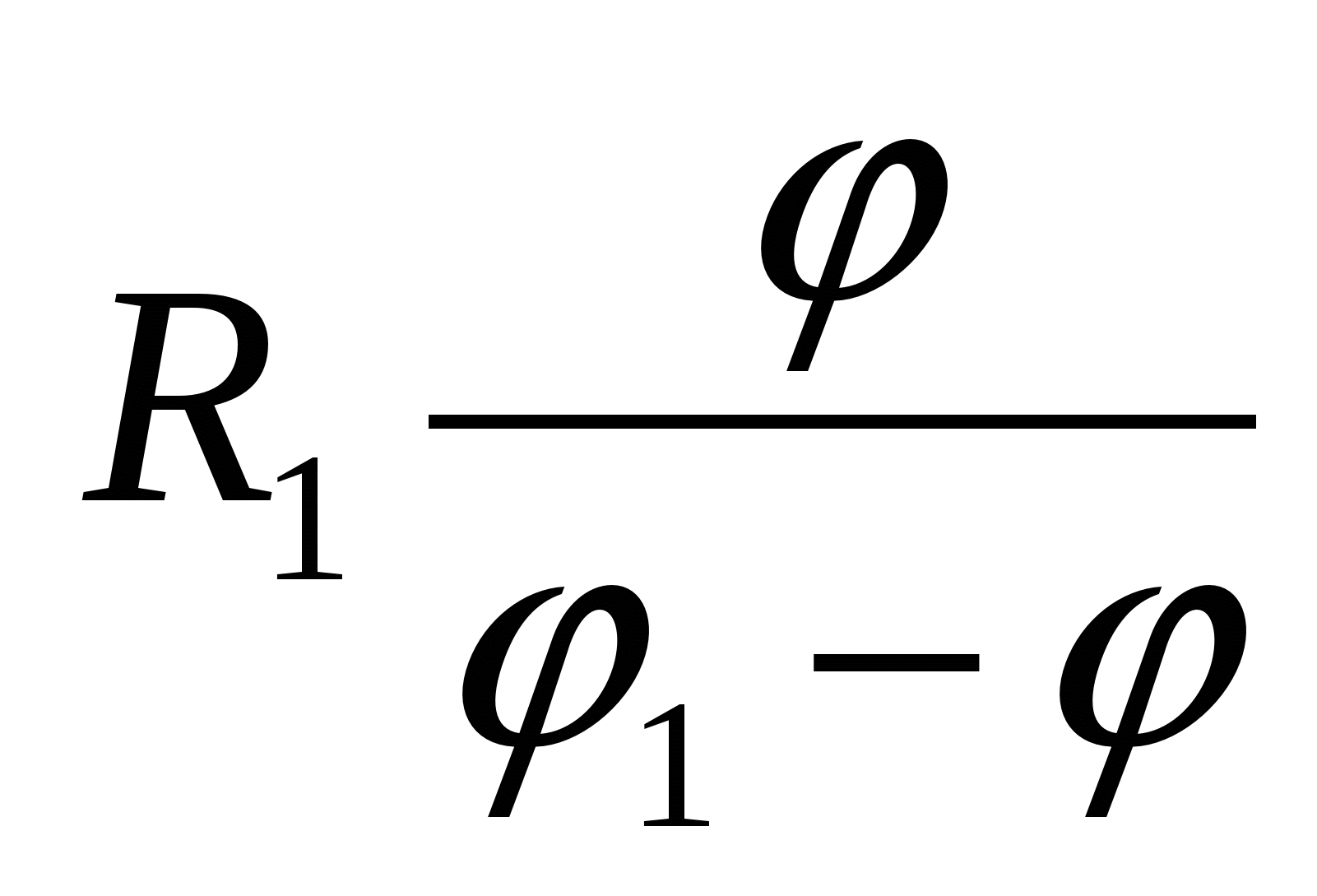 | 5) 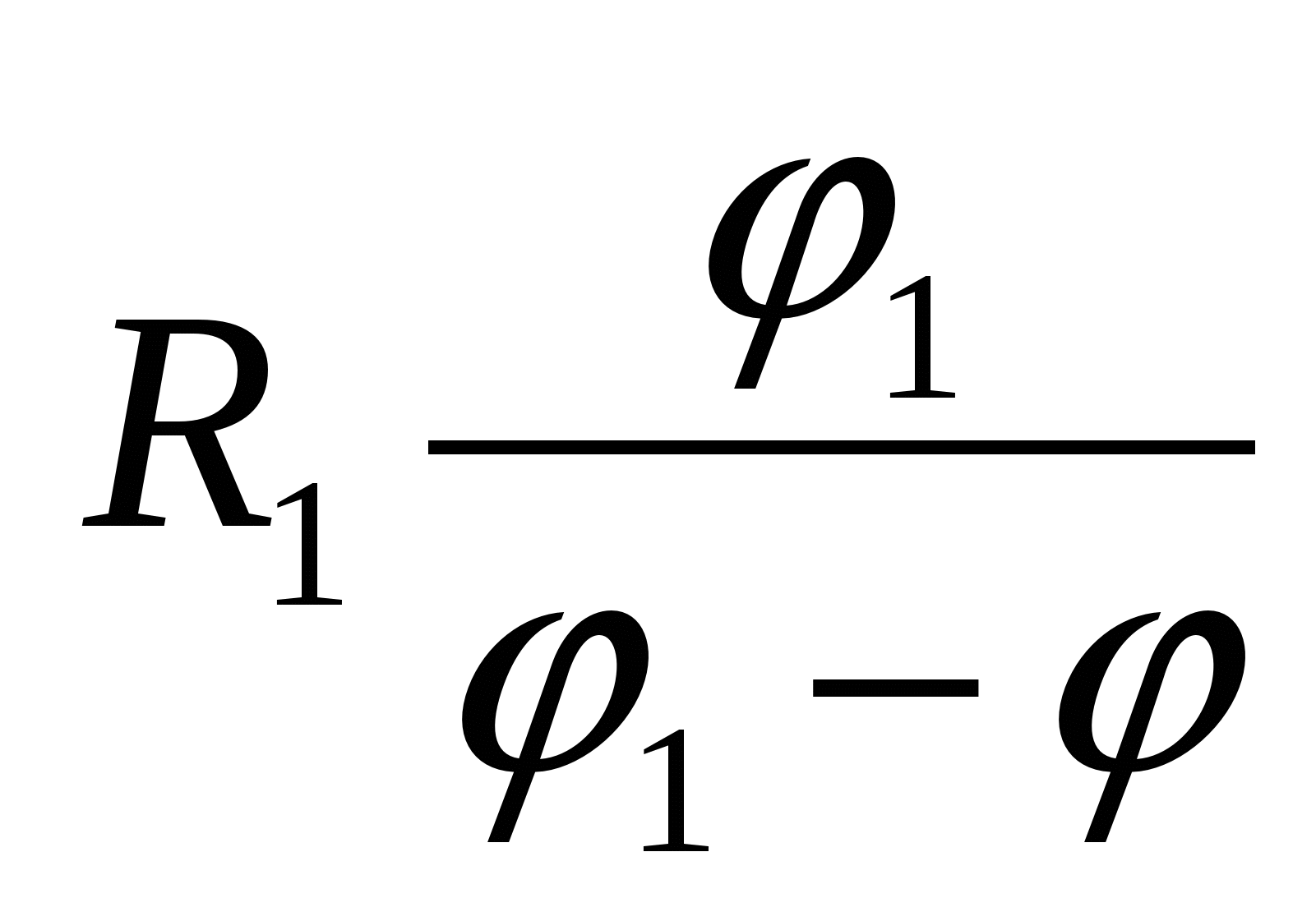 |
7
(CT 2001. 2. pārbaudījums. A 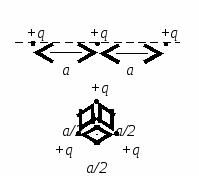 19). Cik daudz jāstrādā, lai trīs vienādi punktu pozitīvi lādiņi q, kas atrodas vakuumā pa vienu taisnu līniju attālumā a
viens no otra, novietoti vienādmalu trijstūra ar malu virsotnēs a/2.
19). Cik daudz jāstrādā, lai trīs vienādi punktu pozitīvi lādiņi q, kas atrodas vakuumā pa vienu taisnu līniju attālumā a
viens no otra, novietoti vienādmalu trijstūra ar malu virsotnēs a/2.
7.1. Ir divi elektrodi koncentrisku sfēru formā ar rādiusiem a(iekšējais) un b(ārējais). Šādu sistēmu sauc par sfērisku kondensatoru. Atrodiet jebkura lauka punkta potenciālu starp elektrodiem.
7.2. Aprēķināt potenciālu elektriskais lauks dipols.
7.3. Atrodiet lauka potenciālu lādiņu sistēmai, kas atrodas tilpumā ar lineāriem izmēriem l, attālumos .
7.4. Uzzīmējiet divu uzlādētu sfēru sistēmas potenciālu diagrammu.
7.5. Aprēķiniet rādiusa lodītes lauka potenciālu a, vienmērīgi uzlādēts pēc tilpuma: a) bumbas iekšpusē; b) ārpus bumbas. Attēlu grafiks 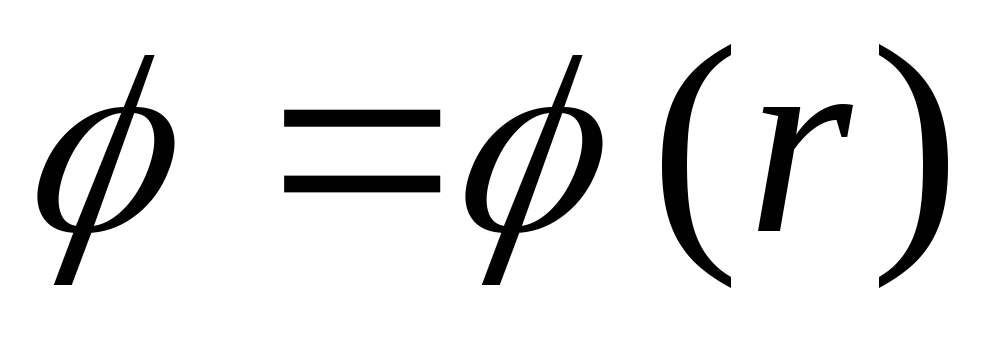 , kur r ir attālums no lodītes centra. Atrisiniet problēmu, integrējot Puasona vienādojumu sfēriskās koordinātās, kā arī izmantojot sakarību starp lauka intensitāti un potenciālu.
, kur r ir attālums no lodītes centra. Atrisiniet problēmu, integrējot Puasona vienādojumu sfēriskās koordinātās, kā arī izmantojot sakarību starp lauka intensitāti un potenciālu.
7.6. Gar tievu stieples gredzenu ar rādiusu R vienmērīgi sadalīts lādiņš q. Izpētīt elektriskā lauka potenciāla atkarību no gredzena ass no attāluma līdz tā centram. Atrodiet spriedzi kā potenciālo gradientu.
7.7. Sfēras rādiuss  , vienmērīgi uzlādēts ar lādiņu
, vienmērīgi uzlādēts ar lādiņu 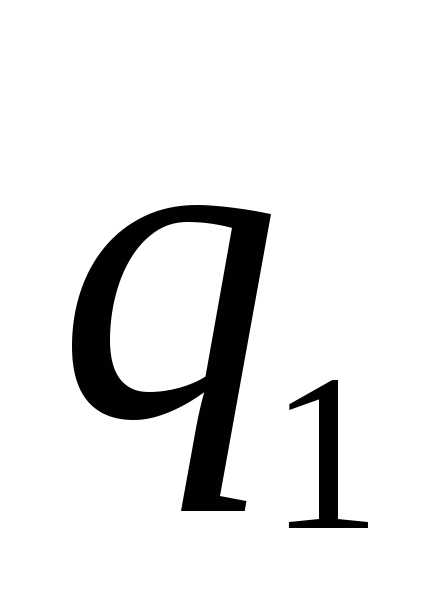 , ko ieskauj plāna koncentriska rādiusa sfēra
, ko ieskauj plāna koncentriska rādiusa sfēra 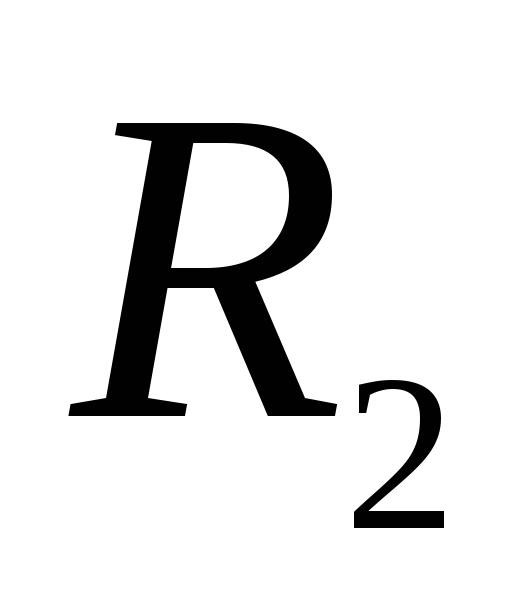 . Kāda maksa
. Kāda maksa 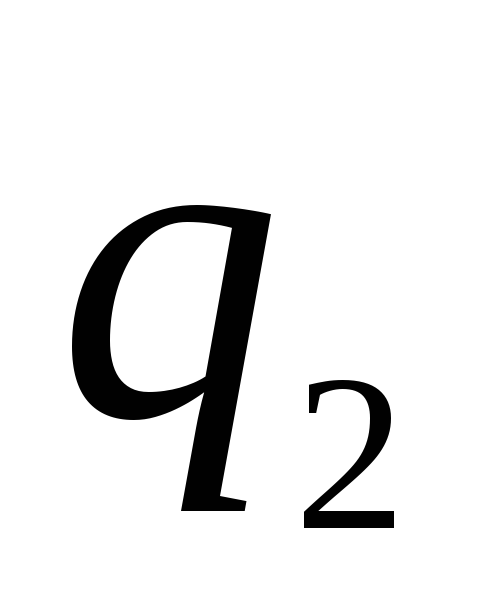 vajag informēt ārējo sfēru, lai iekšējās sfēras potenciāls attiecībā pret bezgalību zustu? Uzlādē
vajag informēt ārējo sfēru, lai iekšējās sfēras potenciāls attiecībā pret bezgalību zustu? Uzlādē 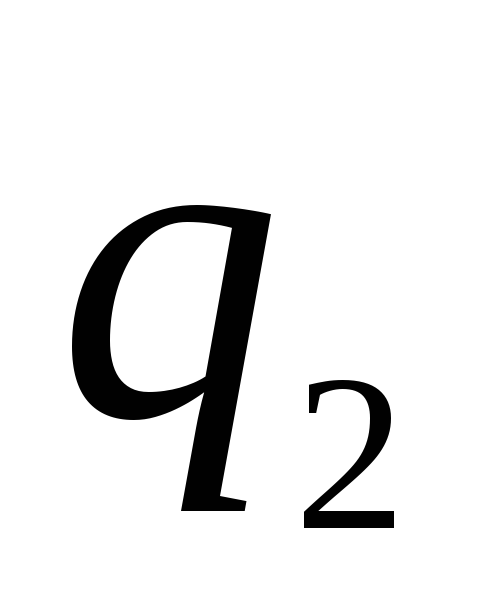 arī vienmērīgi sadalīts pa tās virsmu.
arī vienmērīgi sadalīts pa tās virsmu.
Problēmu risināšana
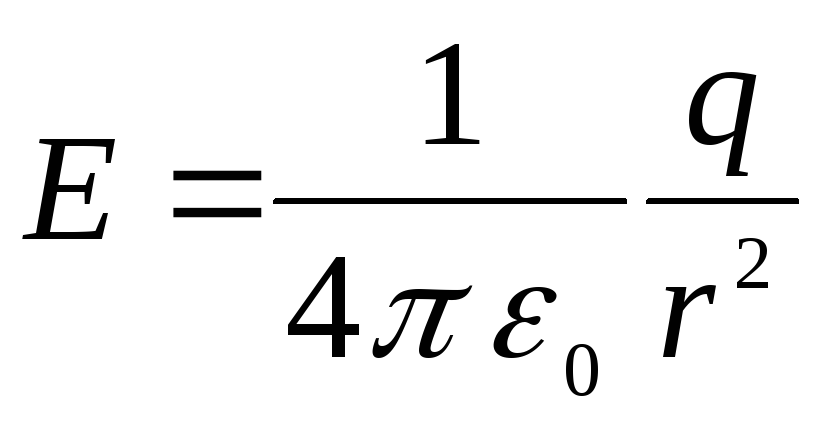
un tāpēc mainās telpā tāpat kā punktveida lādiņa lauka gadījumā, no kā izriet, ka potenciālā starpība starp iekšējo sfēru un jebkuru lauka punktu, kas atrodas tālumā. r no kondensatora centra, ir vienāds ar
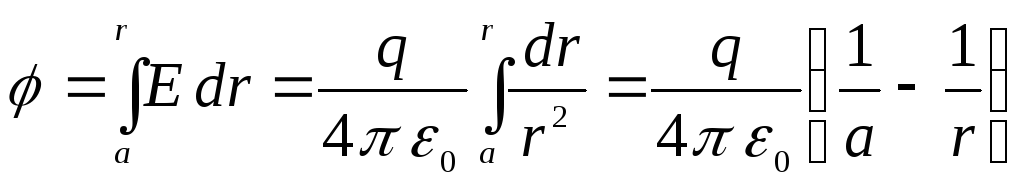 .
.
Iespējamā atšķirība 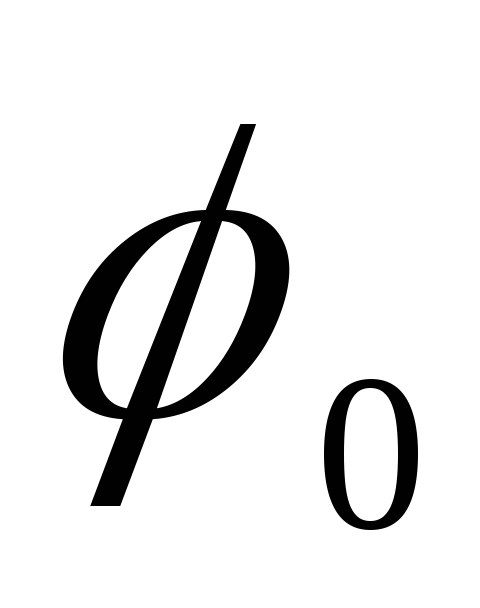 starp elektrodiem (sfērām) būs vienāds ar
starp elektrodiem (sfērām) būs vienāds ar
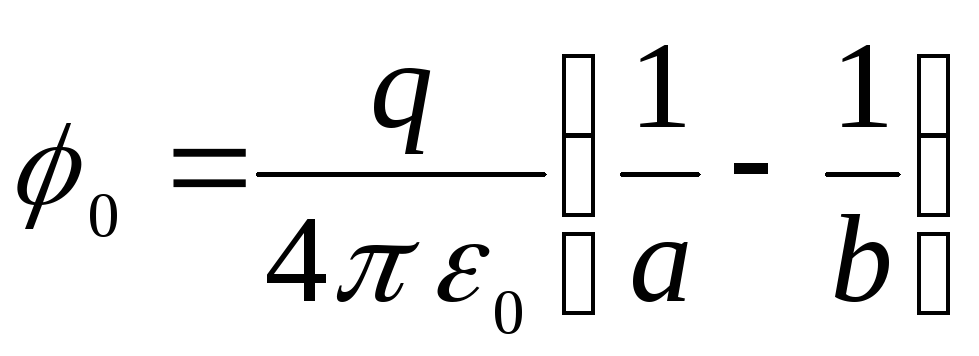 .
.
No šīm divām formulām izriet
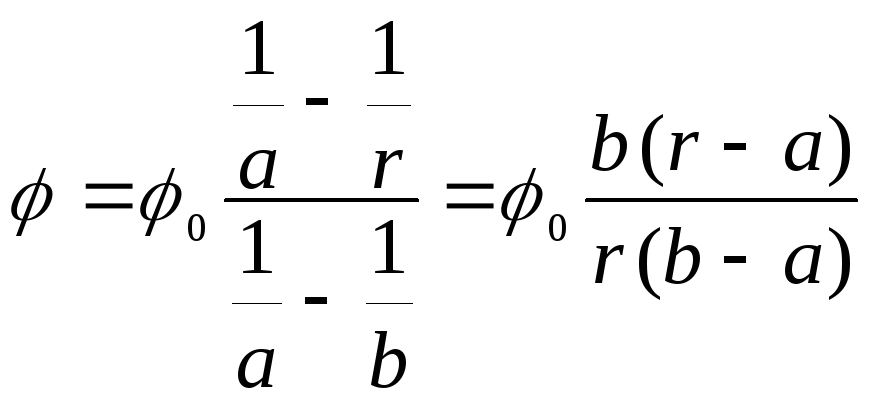 .
.
Izmērot 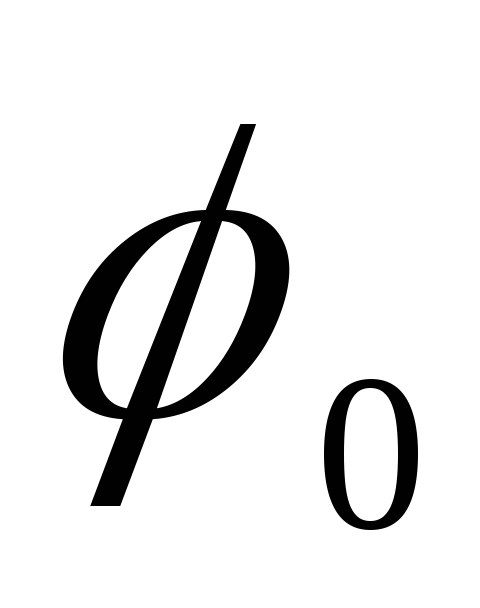 starp elektrodiem varat aprēķināt jebkura lauka punkta potenciālu.
starp elektrodiem varat aprēķināt jebkura lauka punkta potenciālu.
7.2. Ļaujiet sistēmai maksas 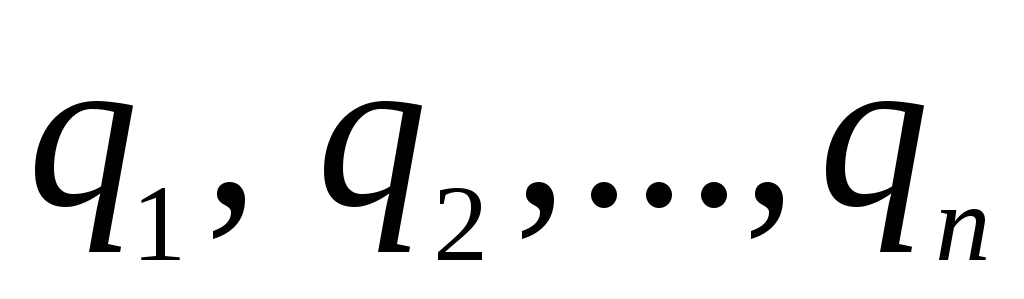 atrodas tilpumā ar lineārajiem izmēriem l. Atradīsim šīs lādiņu sistēmas radītā lauka potenciālu attālumos r, kas ir lieli salīdzinājumā ar l. Mēs izvēlamies koordinātu O izcelsmi lādiņu sistēmas aizņemtajā tilpumā un nosaka lādiņu atrašanās vietu, izmantojot rādiusus - vektorus
atrodas tilpumā ar lineārajiem izmēriem l. Atradīsim šīs lādiņu sistēmas radītā lauka potenciālu attālumos r, kas ir lieli salīdzinājumā ar l. Mēs izvēlamies koordinātu O izcelsmi lādiņu sistēmas aizņemtajā tilpumā un nosaka lādiņu atrašanās vietu, izmantojot rādiusus - vektorus 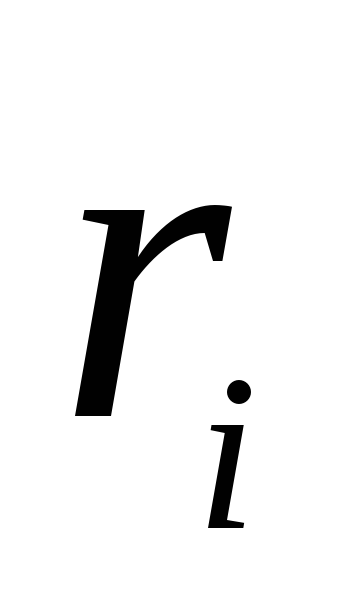 (Attēls ___ parāda vienu no rādiusa vektoriem
(Attēls ___ parāda vienu no rādiusa vektoriem 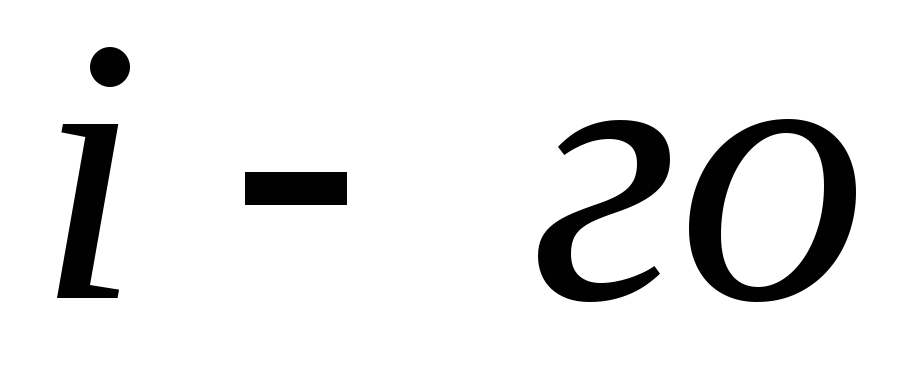 maksa). Potenciāls punktā, ko nosaka rādiusa vektors
maksa). Potenciāls punktā, ko nosaka rādiusa vektors 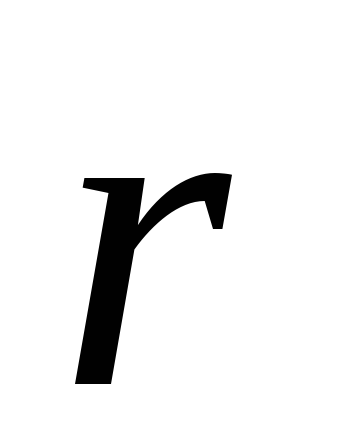 , ir vienāds ar
, ir vienāds ar
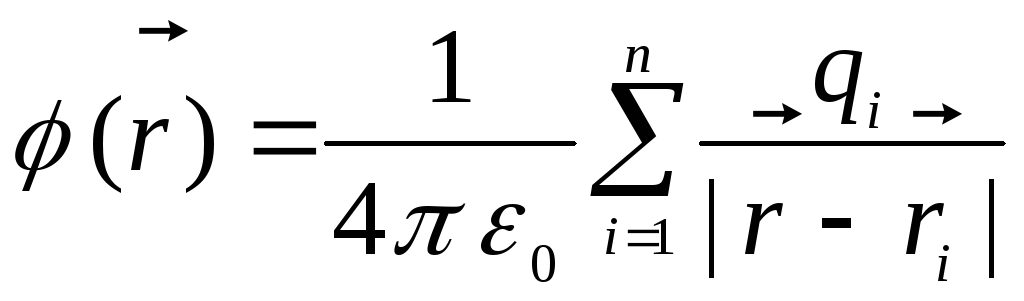 .
.
Jo 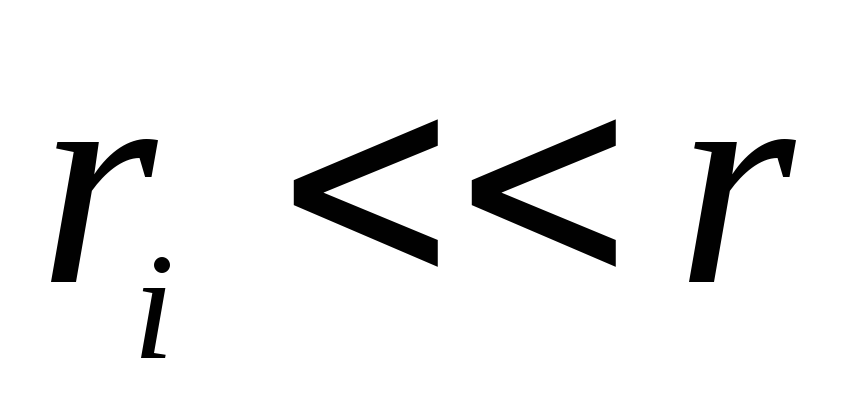 , tad mēs varam to ievietot
, tad mēs varam to ievietot
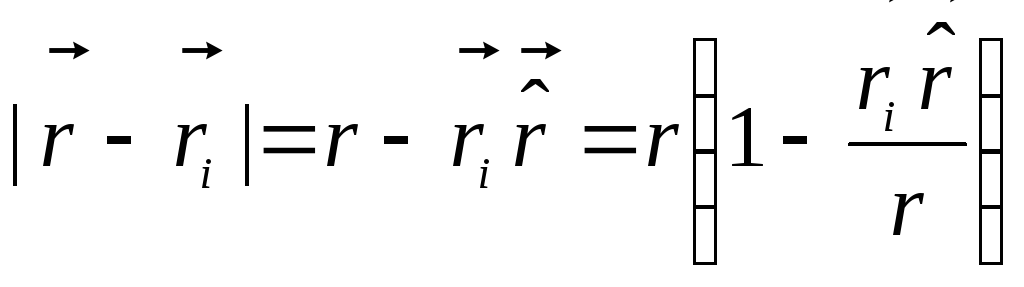
(simbols 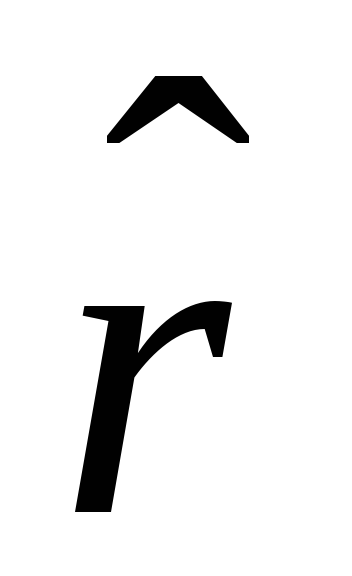 mēs apzīmējām vienības vektoru). Tad
mēs apzīmējām vienības vektoru). Tad
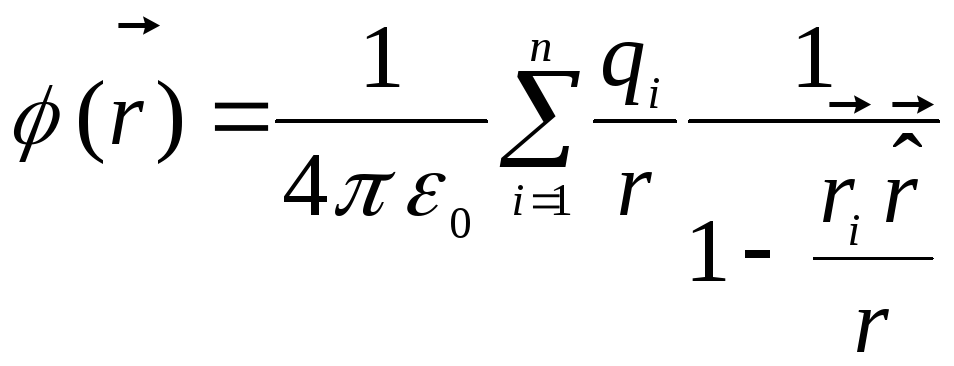 .
.
Izmantosim formulu
![]()
plkst 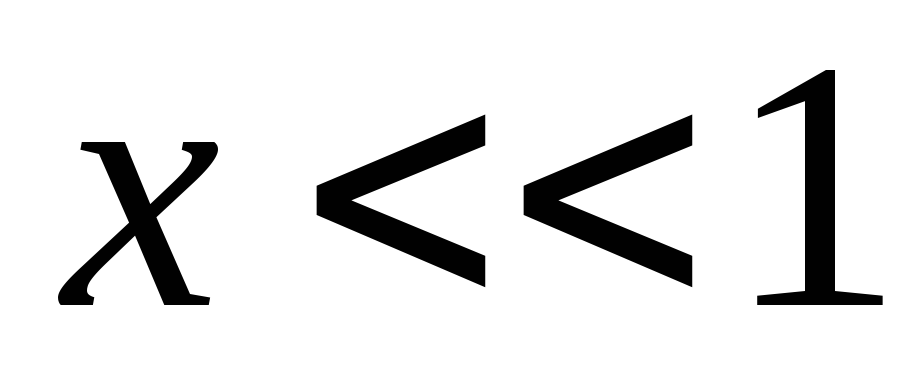 .
.
Tagad mēs varam rakstīt
Šīs izteiksmes pirmais termins ir punktveida lādiņa lauka potenciāls ar vērtību 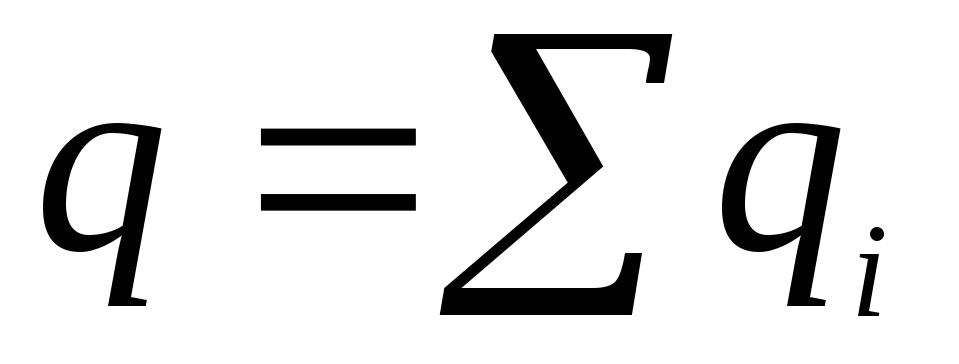 . Otrajam terminam ir tāda pati forma kā izteiksmei, kas nosaka dipola lauka potenciālu. Dipola elektriskā momenta lomu spēlē daudzums
. Otrajam terminam ir tāda pati forma kā izteiksmei, kas nosaka dipola lauka potenciālu. Dipola elektriskā momenta lomu spēlē daudzums
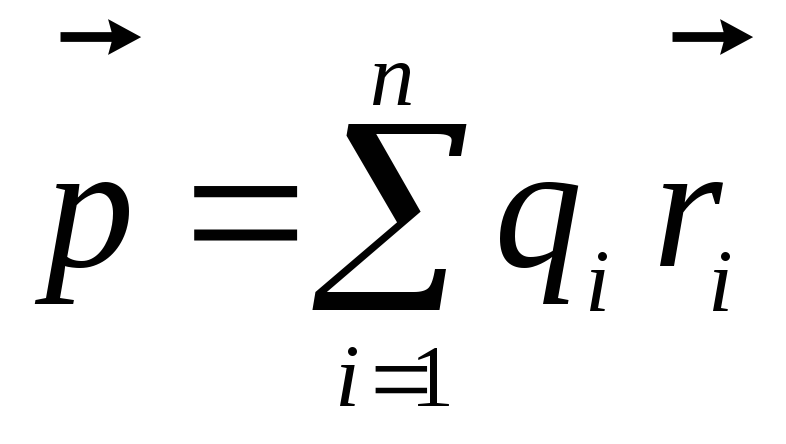 ,
,
ko sauc par lādiņu sistēmas elektrisko dipola momentu.
7.3. Ja lauku veido vairāki lādiņi, tad šī lauka potenciāls ir vienāds ar atsevišķu lādiņu radīto lauku potenciālu summu
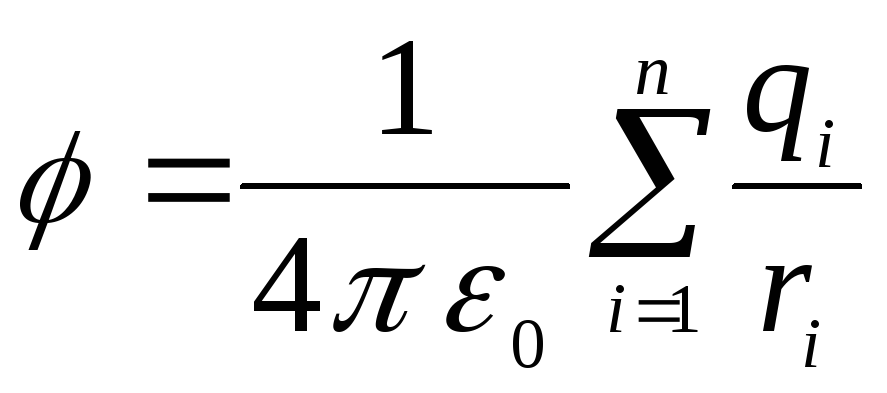
Šeit  ir iegūtā lauka potenciāls aplūkotajā punktā attiecībā pret bezgalību,
ir iegūtā lauka potenciāls aplūkotajā punktā attiecībā pret bezgalību, 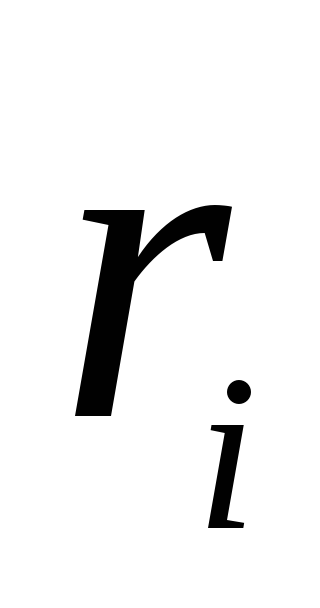 ir attālums no šī punkta līdz
ir attālums no šī punkta līdz 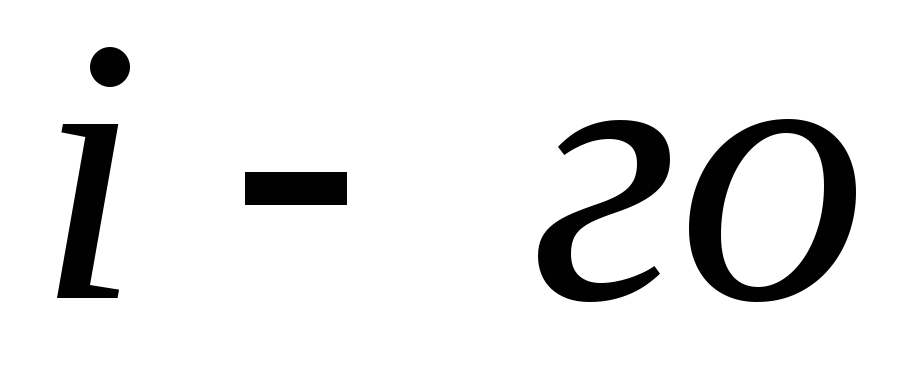 lādiņš, un summēšana tiek veikta pa visām punktu lādiņām.
lādiņš, un summēšana tiek veikta pa visām punktu lādiņām.
Apskatāmajam laukam ir aksiāla simetrija, tāpēc lauka modelis jebkurā plaknē, kas iet caur dipola asi, būs vienāds, un vektors  atrodas šajā plaknē. Punkta M atrašanās vieta attiecībā pret dipolu tiks raksturota, izmantojot rādiusa vektoru
atrodas šajā plaknē. Punkta M atrašanās vieta attiecībā pret dipolu tiks raksturota, izmantojot rādiusa vektoru 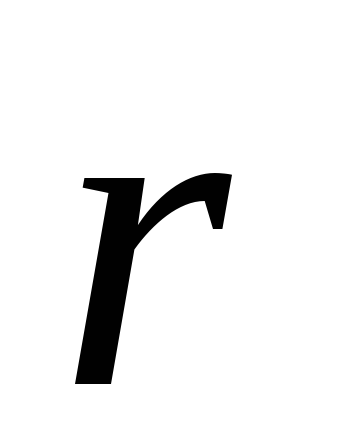 , vai izmantojot polārās koordinātas r un
, vai izmantojot polārās koordinātas r un  . uzlādes pozīcija
. uzlādes pozīcija 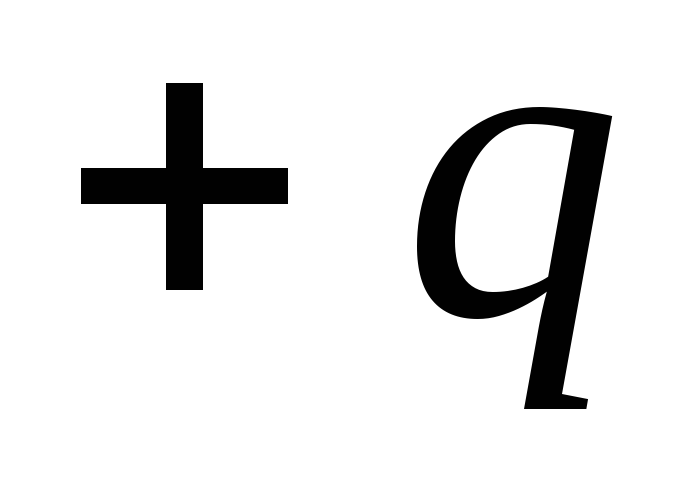 attiecībā pret dipola centru nosaka vektors
attiecībā pret dipola centru nosaka vektors  , un maksa
, un maksa 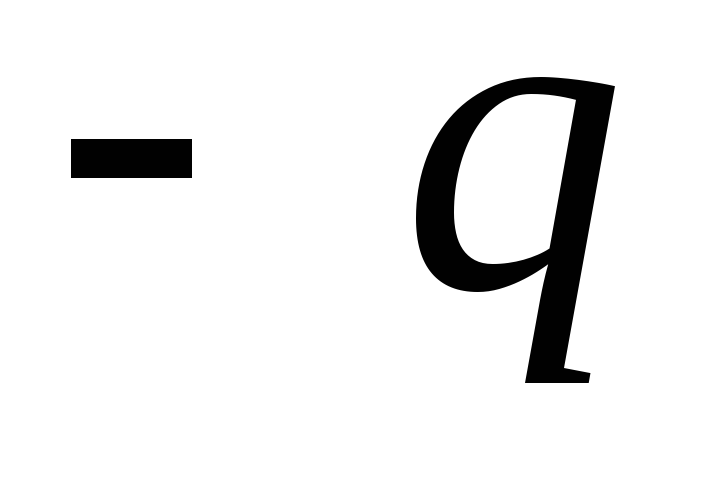 - vektors
- vektors 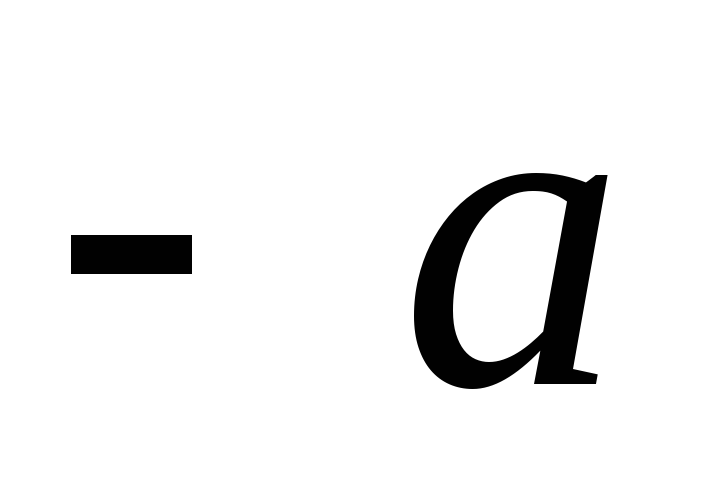 . Ir skaidrs, ka
. Ir skaidrs, ka 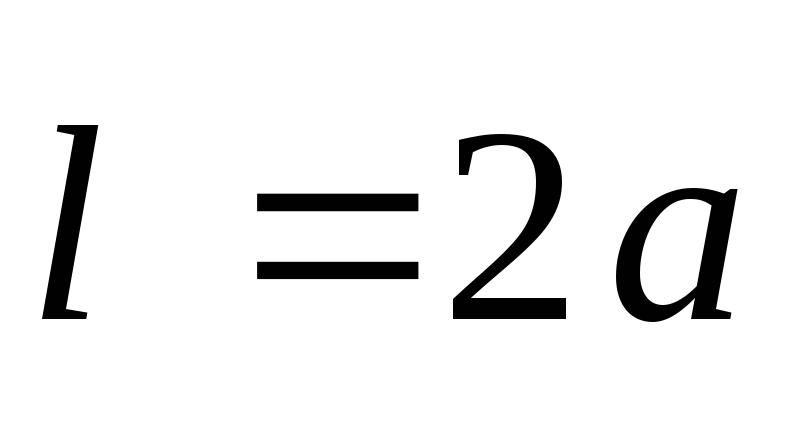 , kur
, kur 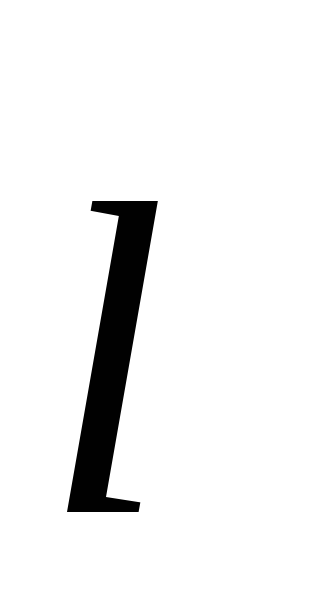 ir dipola roka. Attālumi no maksas
ir dipola roka. Attālumi no maksas 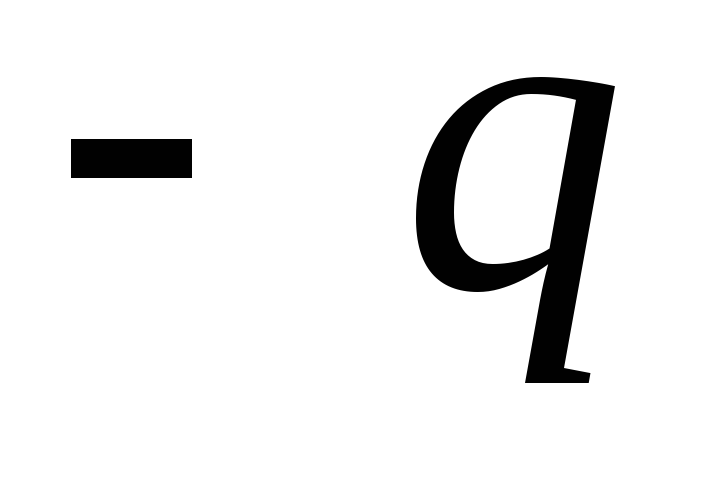 un
un 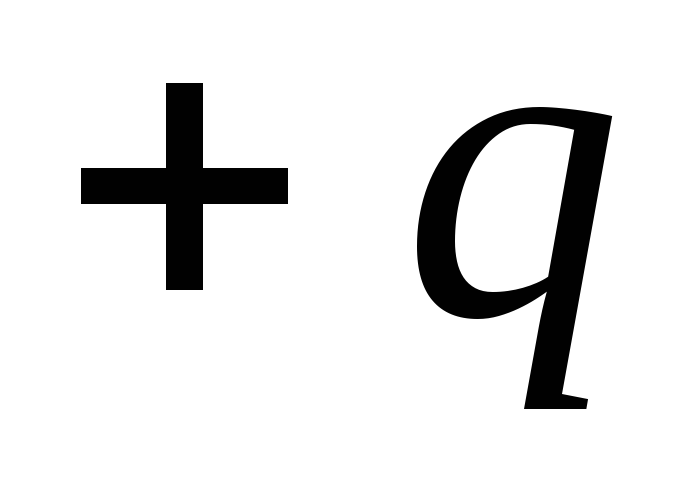 līdz izvēlētajam punktam M apzīmējam attiecīgi,
līdz izvēlētajam punktam M apzīmējam attiecīgi, 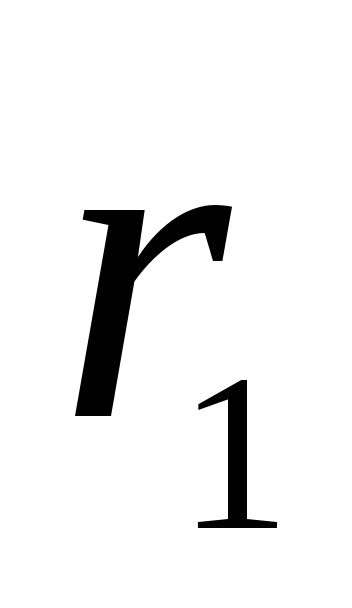 un
un 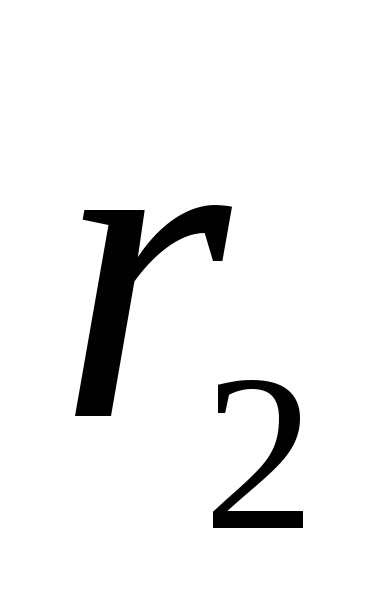 . Jo
. Jo 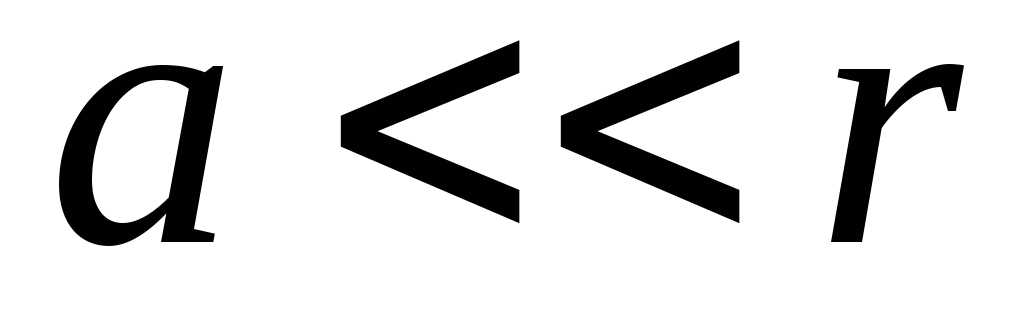 , tad mēs varam to ievietot
, tad mēs varam to ievietot
Potenciāls punktā, ko nosaka rādiusa vektors 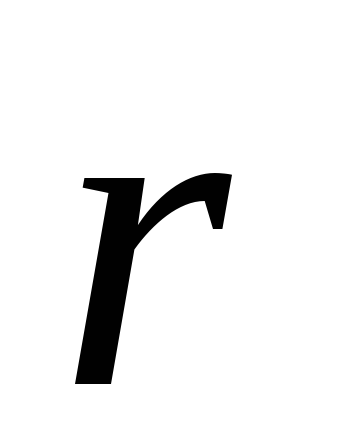 , ir vienāds ar
, ir vienāds ar
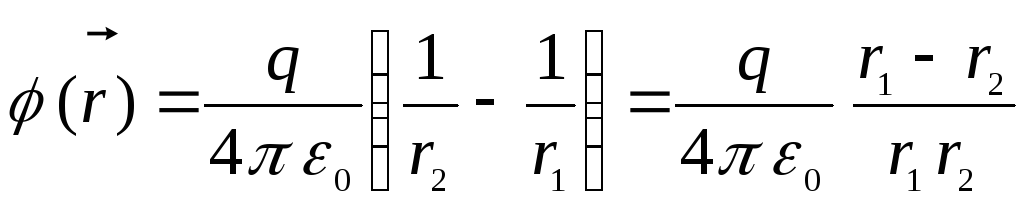 .
.
Darbs 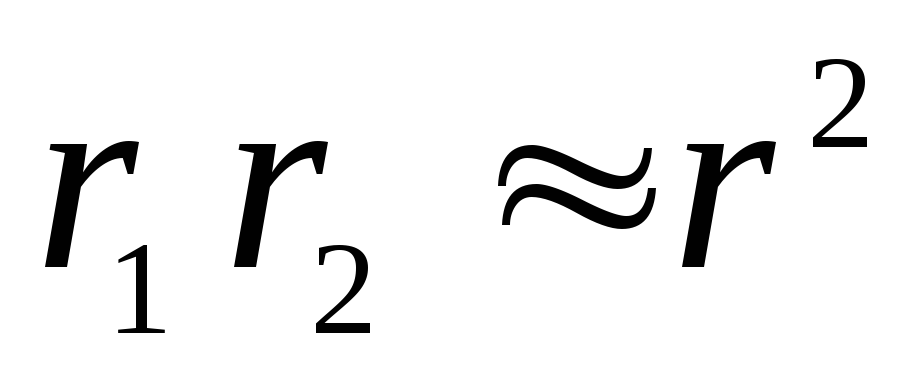 , atšķirība
, atšķirība 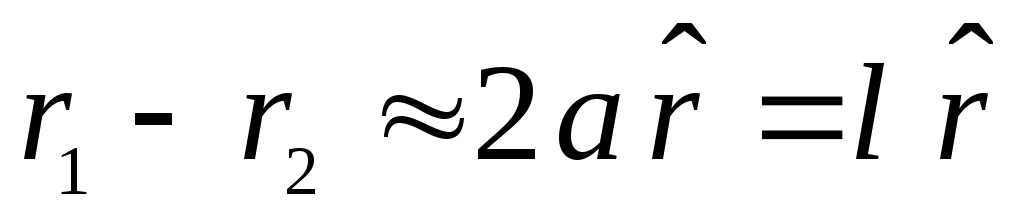 . Sekojoši,
. Sekojoši,
![]() ,
,
kur 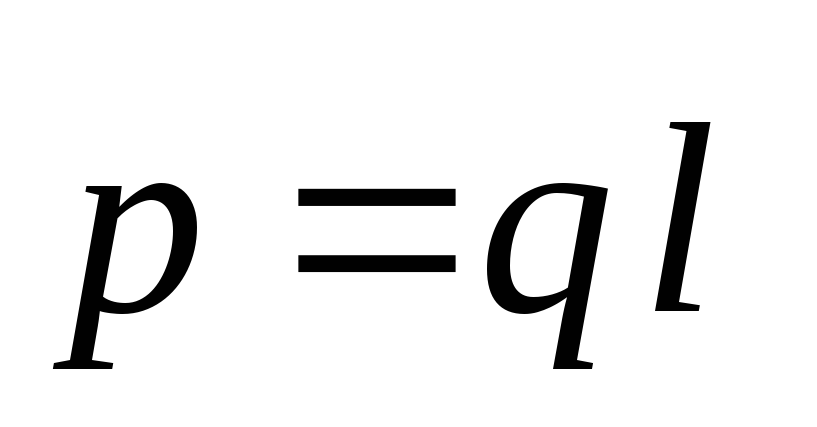 ir dipola elektriskais moments.
ir dipola elektriskais moments.
No šīs formulas var redzēt, ka dipola lauka potenciālu nosaka tā elektriskais moments. Salīdzinot dipola lauka potenciālu ar punktveida lādiņa lauka potenciālu, redzams, ka dipola lauka potenciāls samazinās ar attālumu ātrāk 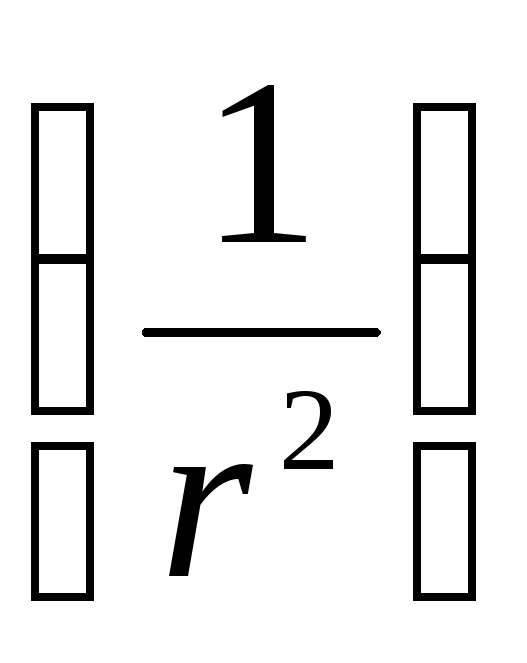 nekā punktveida lādiņa lauka potenciāls
nekā punktveida lādiņa lauka potenciāls 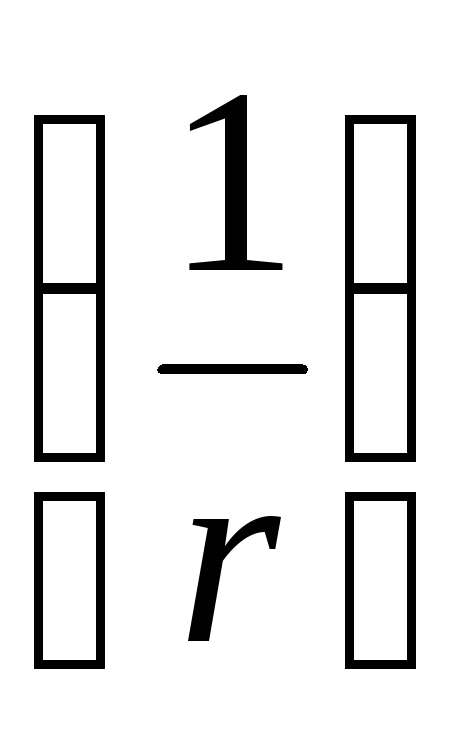 .
.
Attēls ___ parāda to 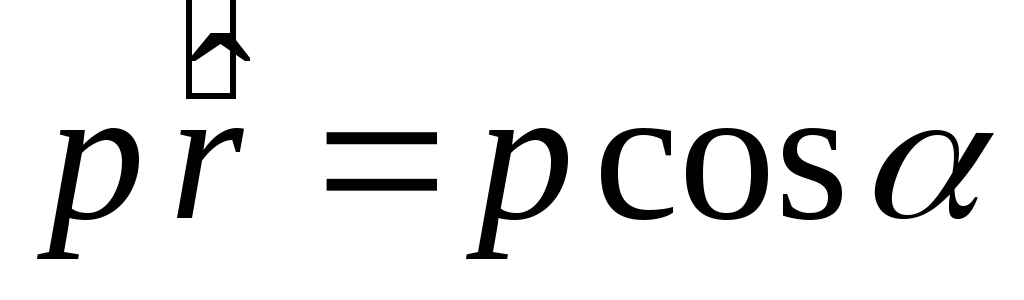 . Tāpēc
. Tāpēc
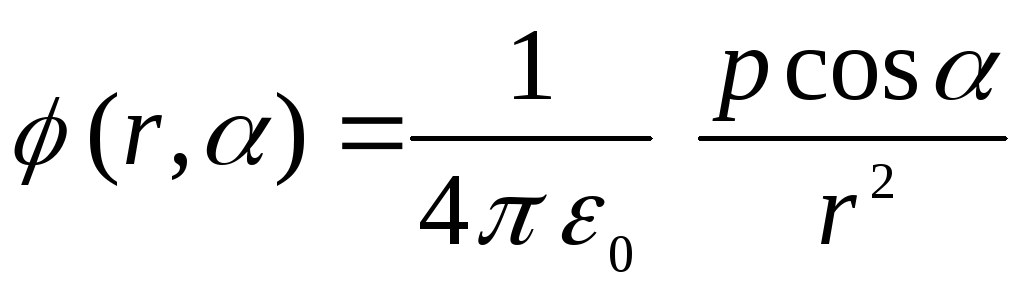 .
.
7.4. Ļaujiet iekšējai sfērai, kuras rādiuss  , ir pozitīvs lādiņš
, ir pozitīvs lādiņš 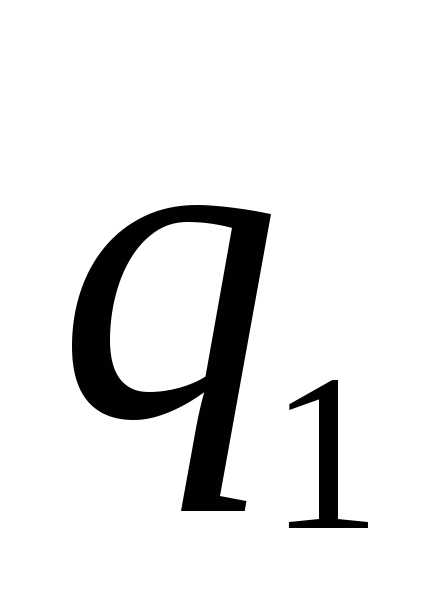 , un ārējais ar rādiusu
, un ārējais ar rādiusu 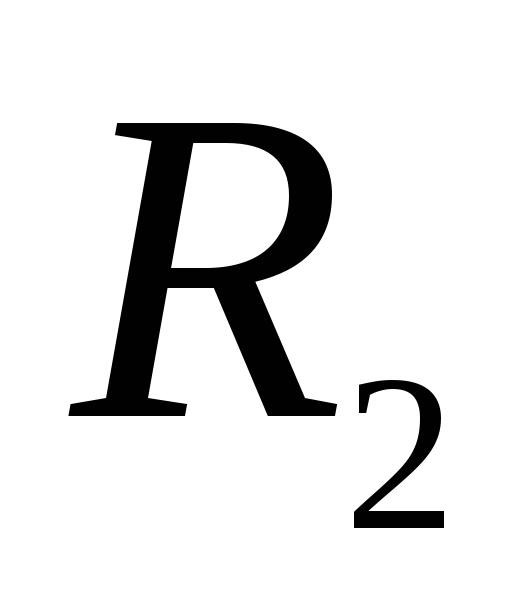 - negatīvs lādiņš
- negatīvs lādiņš 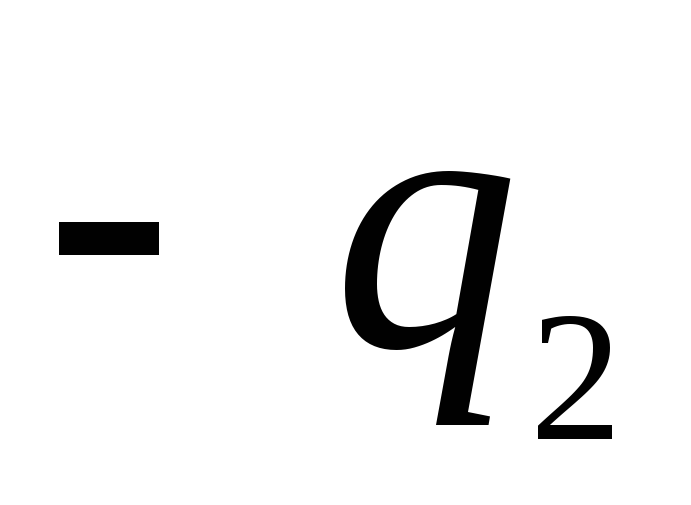 , un
, un 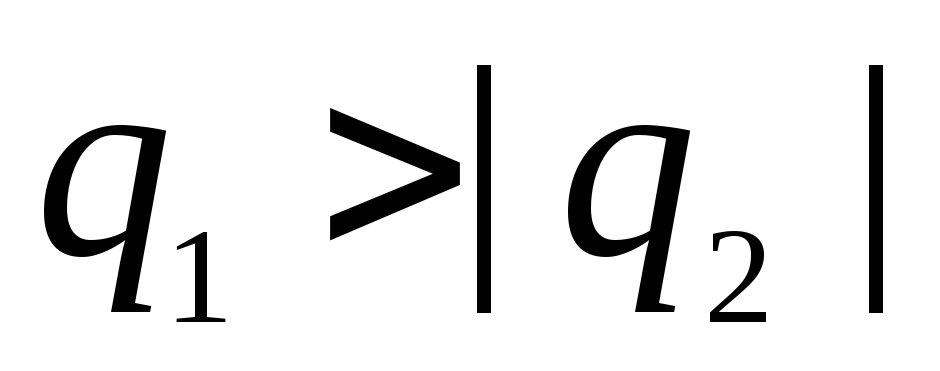 .
.
Ārpus sfērām potenciāls būs vienāds ar
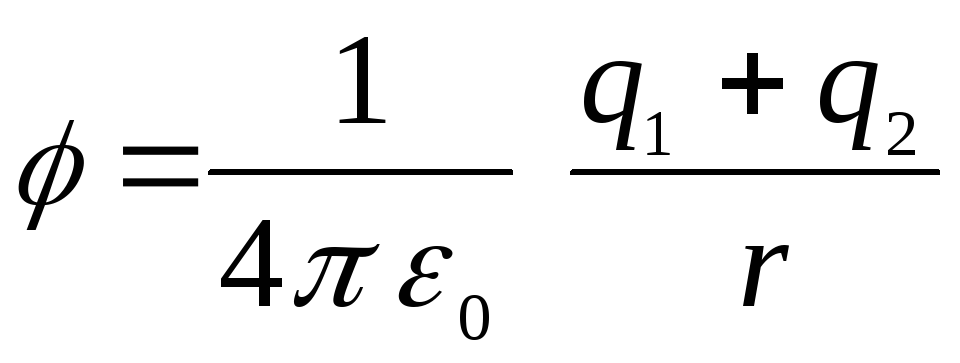 ,
,
jo to kopīgi rada abas sfēras (potenciāls ir ārējo spēku darbs, kas tiek veikts, kad vienības pozitīvais lādiņš pārvietojas no bezgalības uz noteiktu lauka punktu). Darbs, lai pārvietotu vienības pozitīvo lādiņu no bezgalības uz laukumu starp sfērām, būs vienāds ar divu darbu summu: 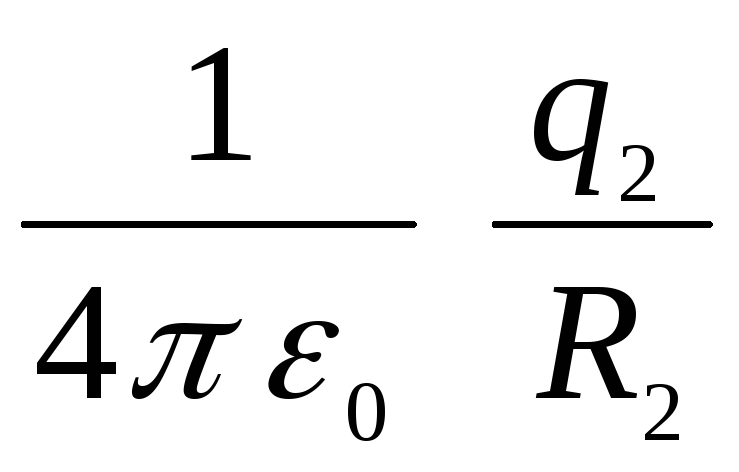 (darbs pret spēkiem, kas iedarbojas no ārējās sfēras ceļā no bezgalības uz tās virsmu) un
(darbs pret spēkiem, kas iedarbojas no ārējās sfēras ceļā no bezgalības uz tās virsmu) un 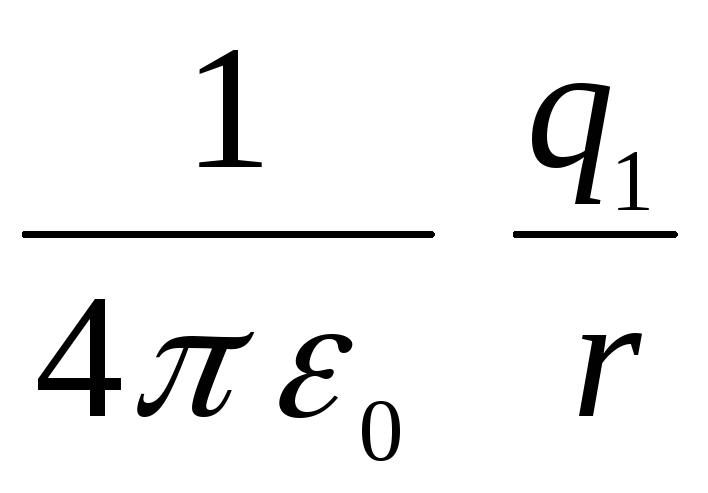 (darbs pret iekšējās sfēras lauku), t.i.
(darbs pret iekšējās sfēras lauku), t.i.
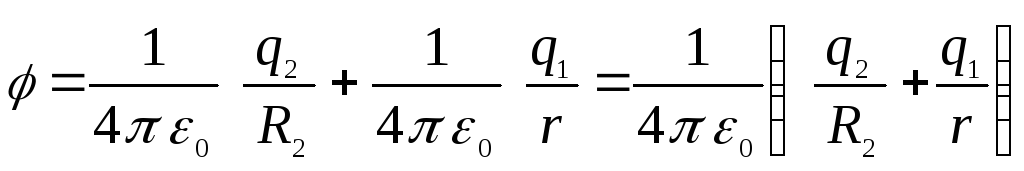 .
.
Mazākās sfēras iekšpusē potenciāls būs nemainīgs un vienāds ar
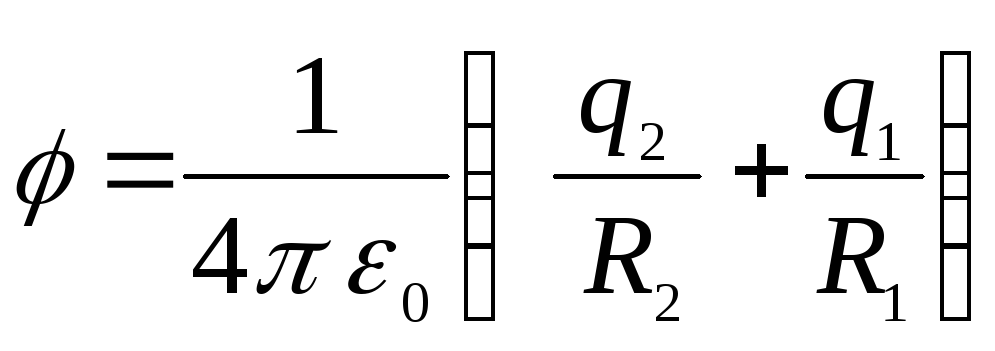 .
.
Pēc pirmās un otrās formulas konstruētais grafiks ir parādīts ____1. attēlā.
Ja sfēru lādiņi ir vienādi pēc lieluma un pretēji pēc zīmes, t.i. 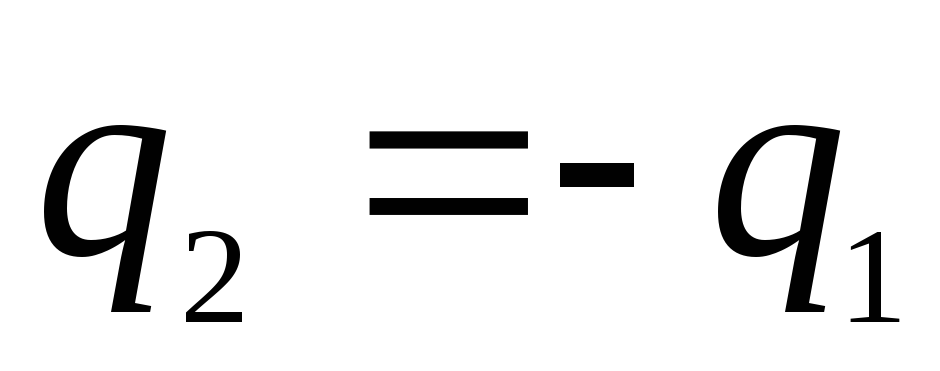 (šādu sistēmu sauc par sfērisku kondensatoru), tad potenciāls ārējā reģionā pazūd, un starp plāksnēm ir
(šādu sistēmu sauc par sfērisku kondensatoru), tad potenciāls ārējā reģionā pazūd, un starp plāksnēm ir
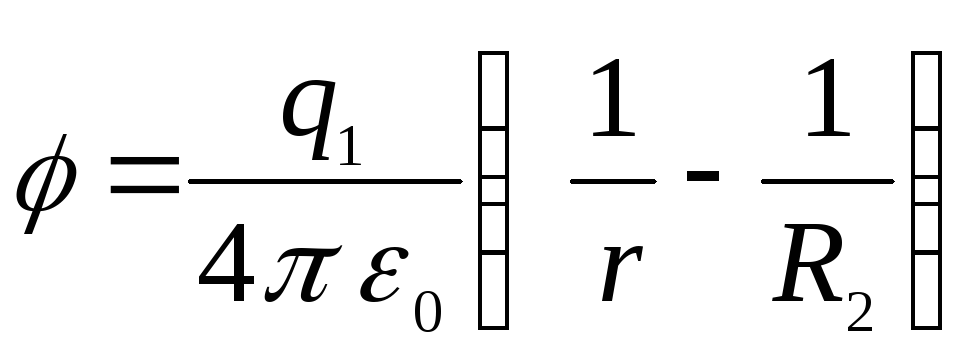 .
.
Izrādās grafiks, kas parādīts ___2. attēlā.
Ja iekšējai sfērai ir negatīvs lādiņš, bet ārējai lādiņš ir pozitīvs, tad grafiks ir apgriezts un izskatās kā attēlā ____3.
7.5. Puasona vienādojuma integrācija sfēriskās koordinātās. Mēs ieviešam sfērisku koordinātu sistēmu 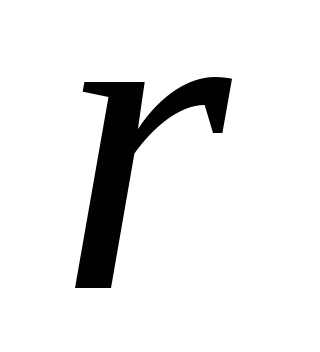 ,
, ,
, , par izcelsmi ņemot bumbiņas centru. Gausa vienādojums diferenciālā formā (Puasona vienādojums), kas nosaka lauka potenciālu, iegūst formu
, par izcelsmi ņemot bumbiņas centru. Gausa vienādojums diferenciālā formā (Puasona vienādojums), kas nosaka lauka potenciālu, iegūst formu
kur 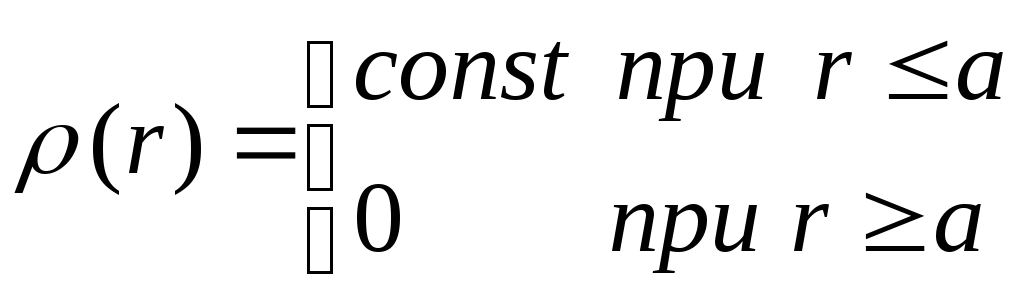 .
.
Sfēriski simetriskā lādiņa sadalījuma dēļ potenciāls  ir atkarīgs tikai no attāluma r un nav atkarīgs no leņķiem
ir atkarīgs tikai no attāluma r un nav atkarīgs no leņķiem  un
un  , t.i.
, t.i. 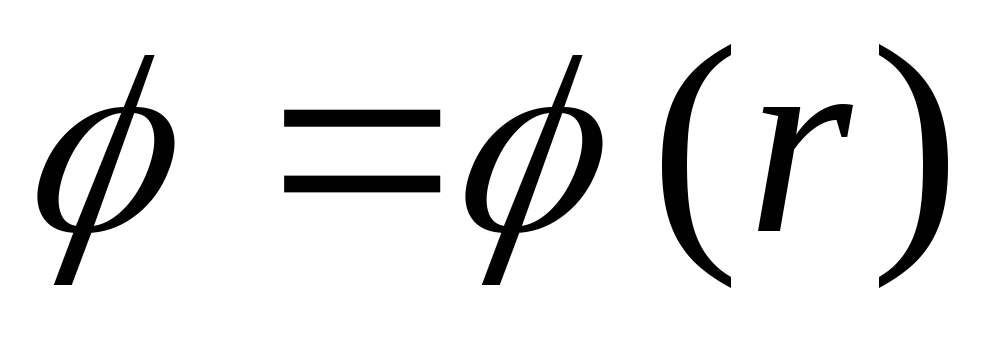 . Tāpēc Puasona vienādojums ir vienkāršots un iegūst formu
. Tāpēc Puasona vienādojums ir vienkāršots un iegūst formu
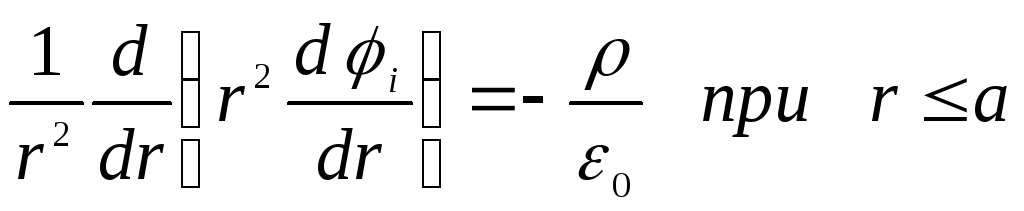
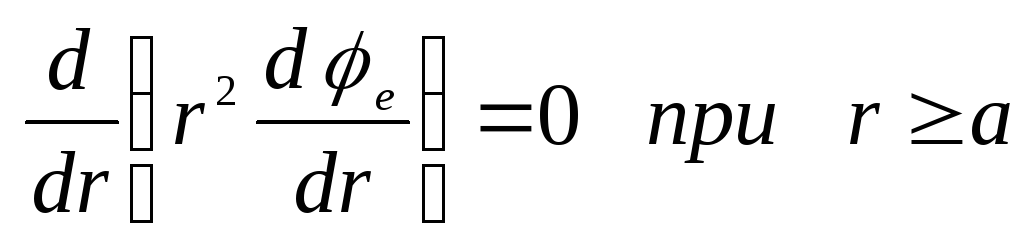 .
.
Šeit cauri 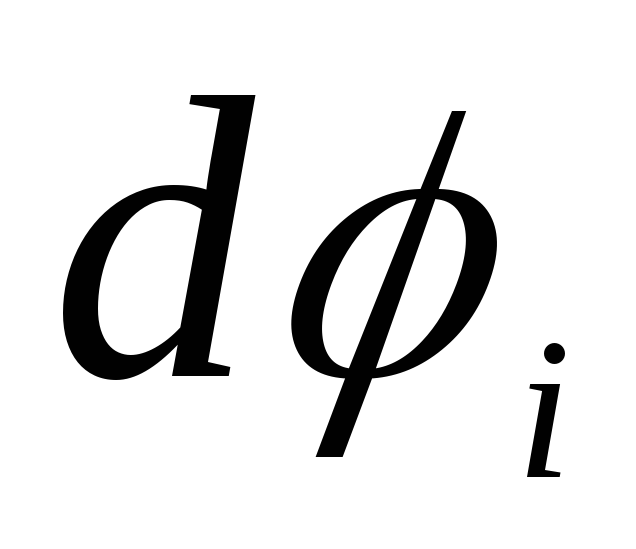 apzīmē potenciālu bumbas iekšpusē un cauri
apzīmē potenciālu bumbas iekšpusē un cauri 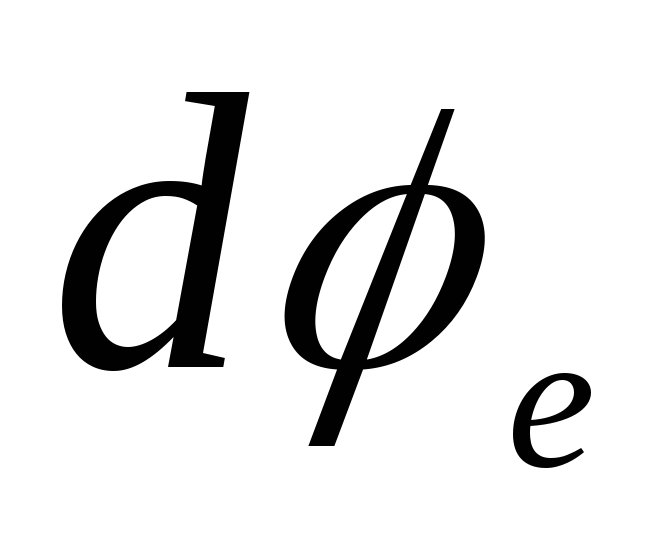 - ārpus bumbas. Integrējot šos vienādojumus, mēs atklājam
- ārpus bumbas. Integrējot šos vienādojumus, mēs atklājam
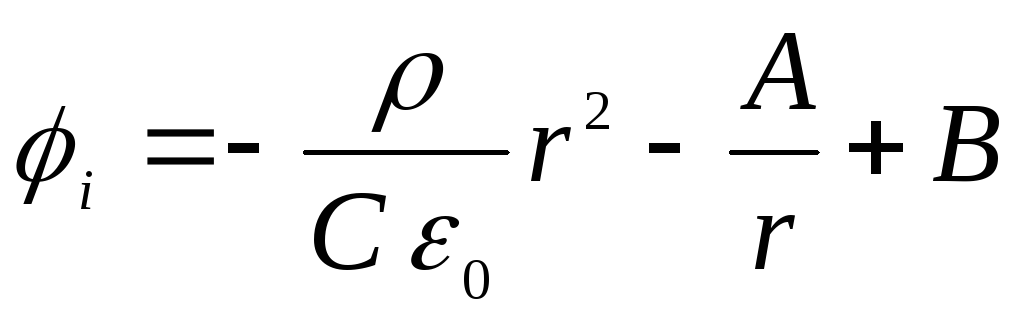 ,
,
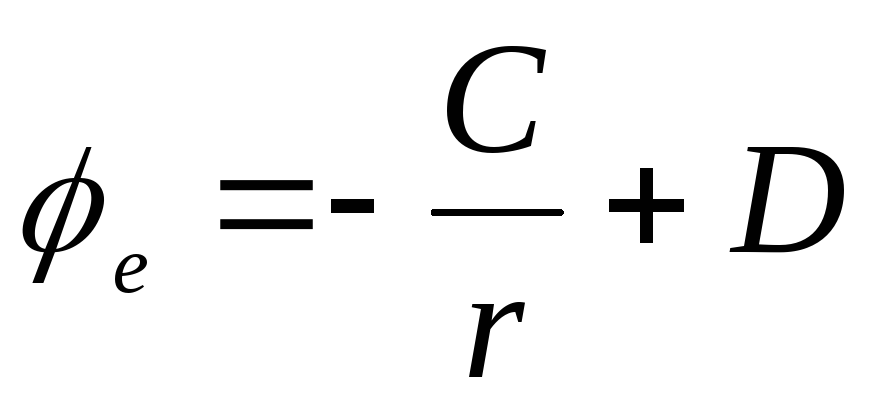 .
.
Konstantes A, B, C, D jānosaka no šādiem robežnosacījumiem.
1) Potenciāls  jāpaliek ierobežotam
jāpaliek ierobežotam 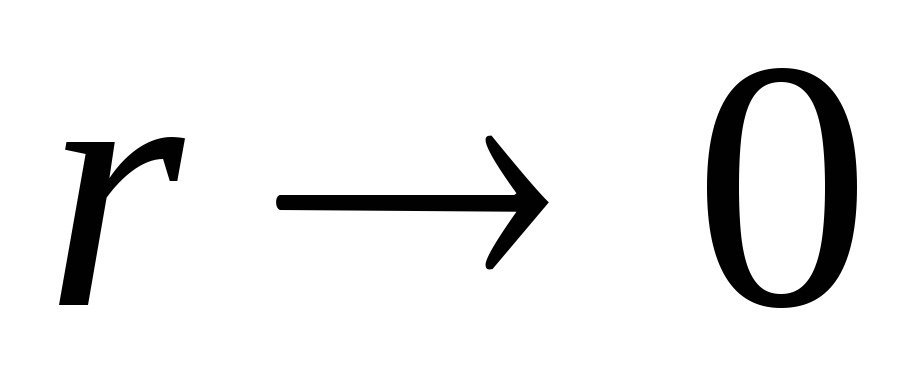 , kas tieši to norāda
, kas tieši to norāda 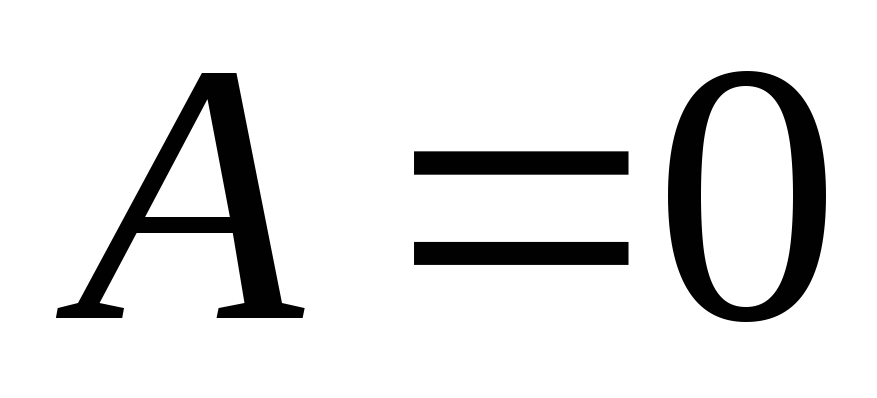 .
.
2)
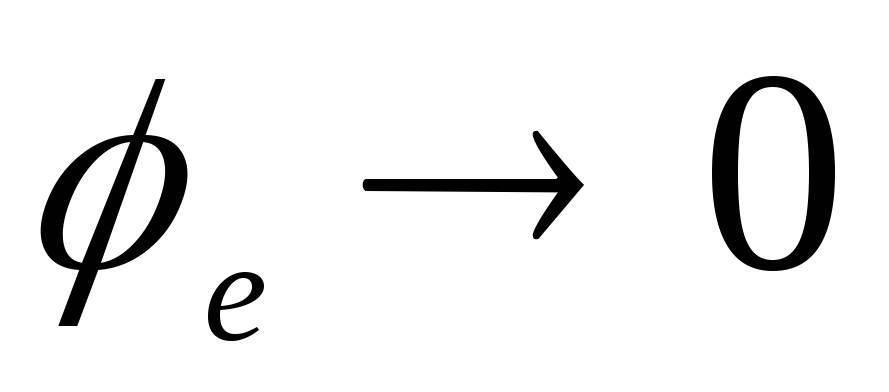 plkst
plkst  , no kurienes tas izriet
, no kurienes tas izriet 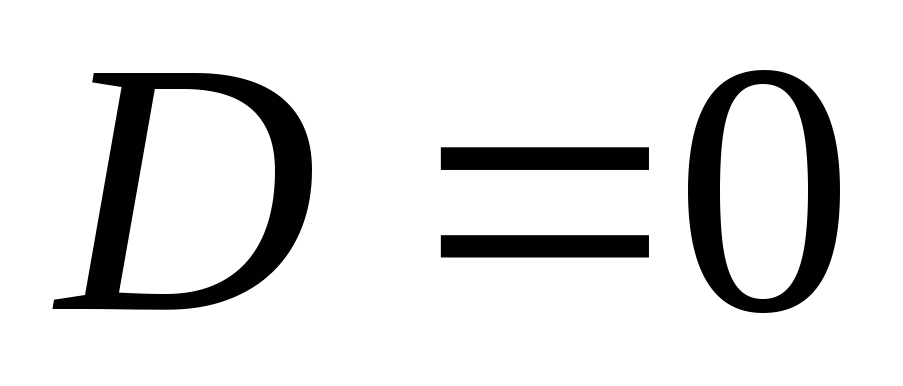 .
.
3) Elektrostatiskā lauka potenciāls ir nepārtraukta koordinātu funkcija, tāpēc tas ir nepieciešams 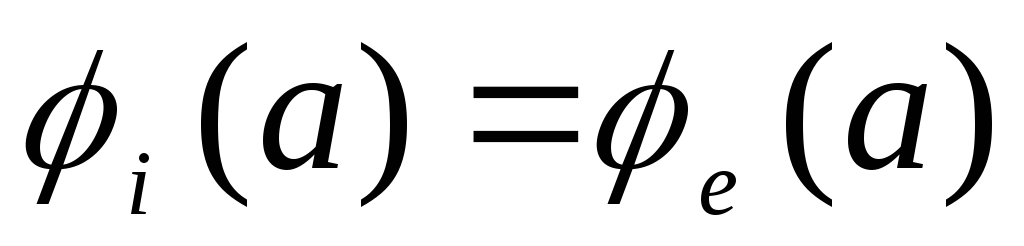 .
.
4) Vektora normālā sastāvdaļa  nedrīkst piedzīvot lēcienu, izejot cauri bumbas virsmai, t.i.
nedrīkst piedzīvot lēcienu, izejot cauri bumbas virsmai, t.i. 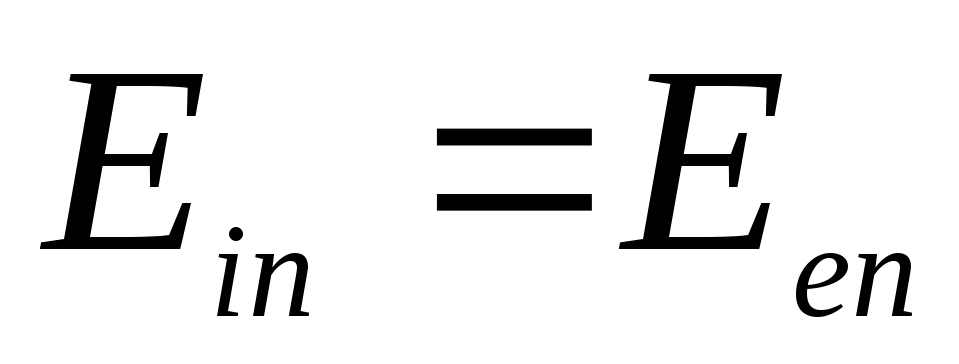 plkst
plkst 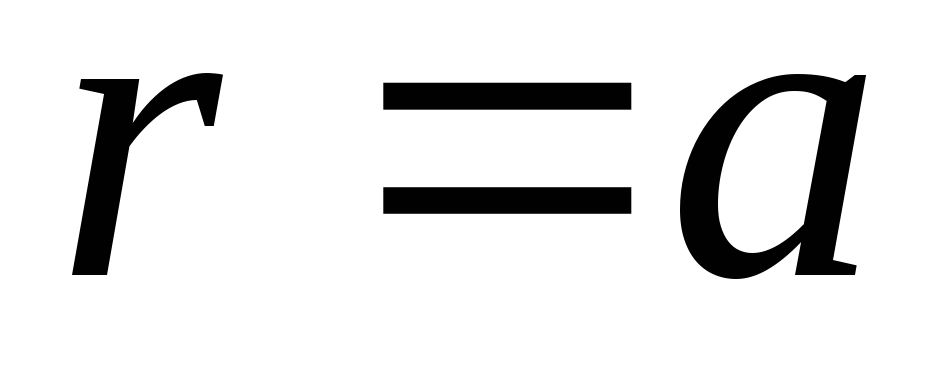 , jo virsmas lādiņa blīvums uz lodītes virsmas ir nulle. Pēdējais nosacījums ir līdzvērtīgs prasībai
, jo virsmas lādiņa blīvums uz lodītes virsmas ir nulle. Pēdējais nosacījums ir līdzvērtīgs prasībai
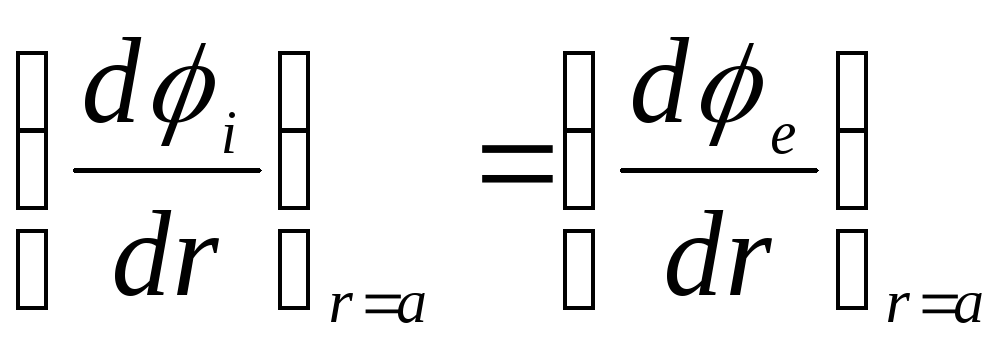 .
.
No pēdējiem diviem nosacījumiem mēs atrodam
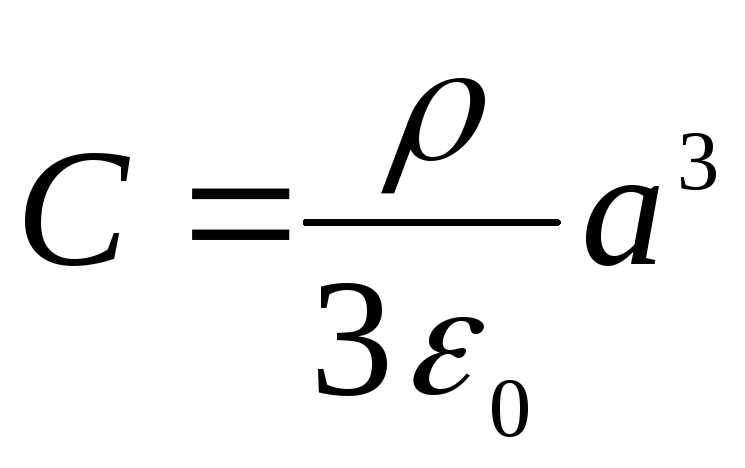 ,
,
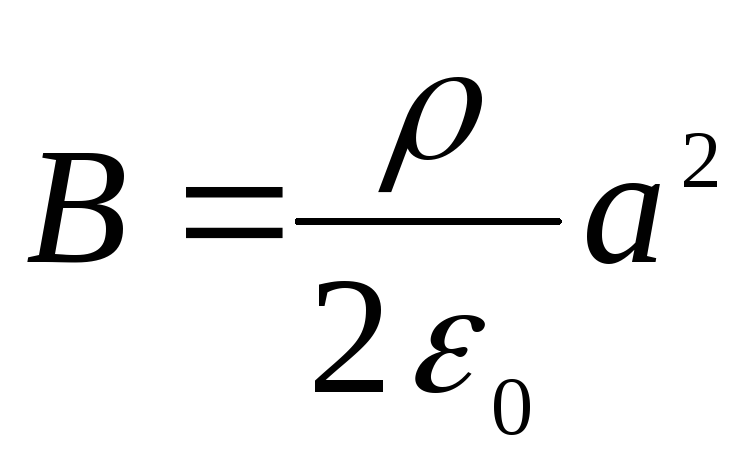 .
.
Beidzot formā ierakstām vēlamos potenciālus
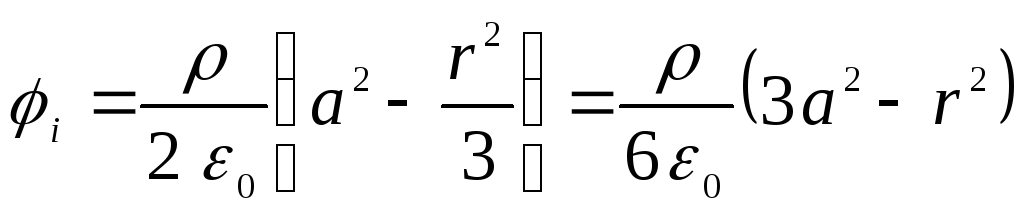 ,
,
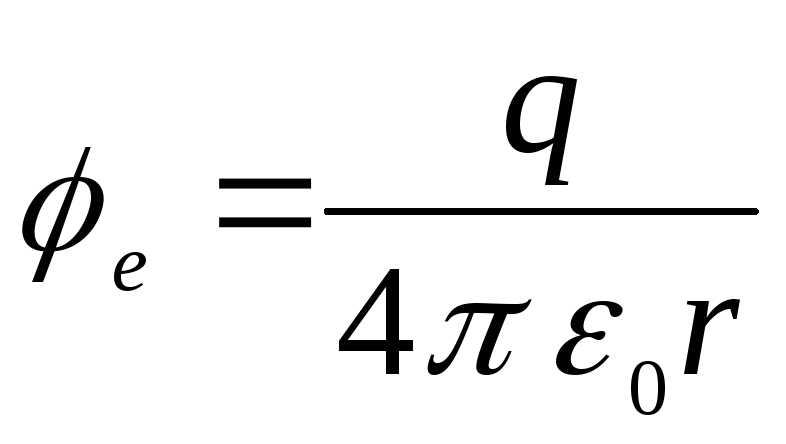 .
.
No šīm formulām var redzēt, ka ārpus lodes lauka potenciāls ir līdzīgs punktveida lādiņa laukam.
Uzzīmēsim grafiku 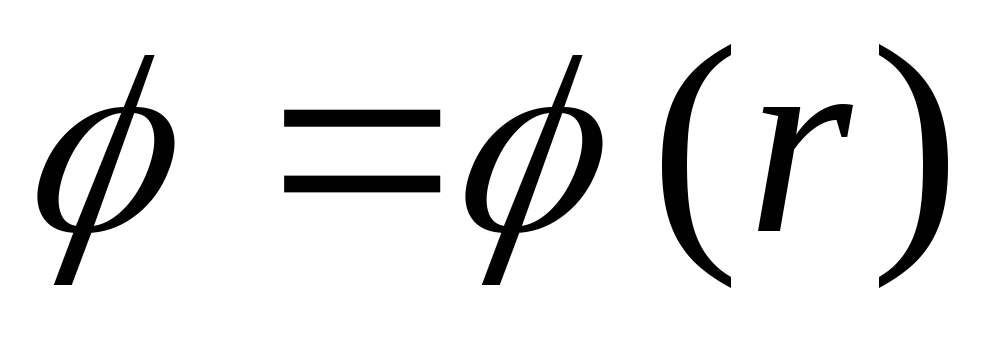 .
.
Ļaujiet 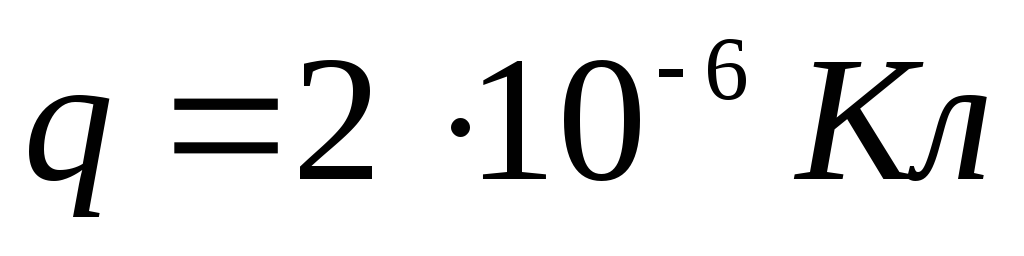 ,
,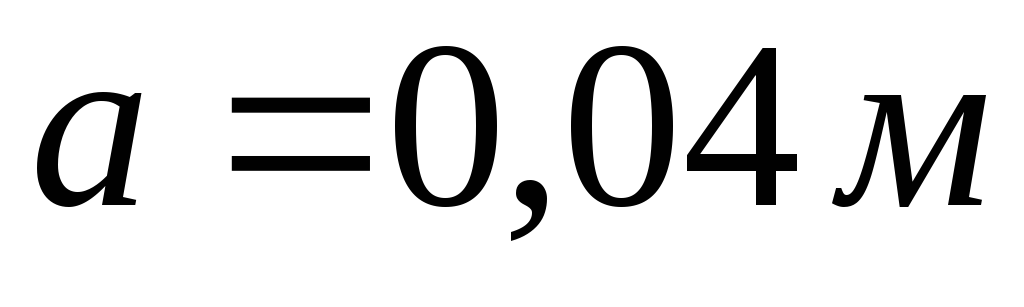 . Atradīsim tilpuma lādiņa blīvumu
. Atradīsim tilpuma lādiņa blīvumu
un attieksme
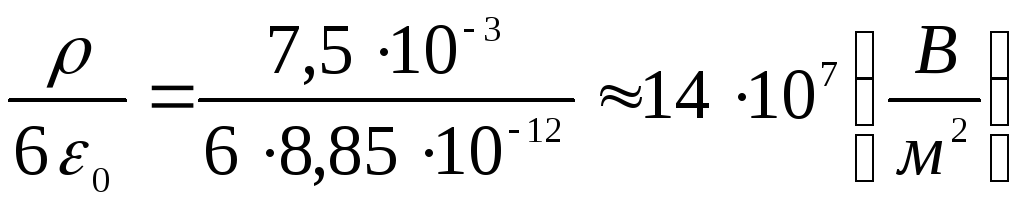 .
.
Tagad mēs varam rakstīt, ka potenciāls sfēras iekšpusē
Taisām galdu
|
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Potenciāls ārpus darbības jomas 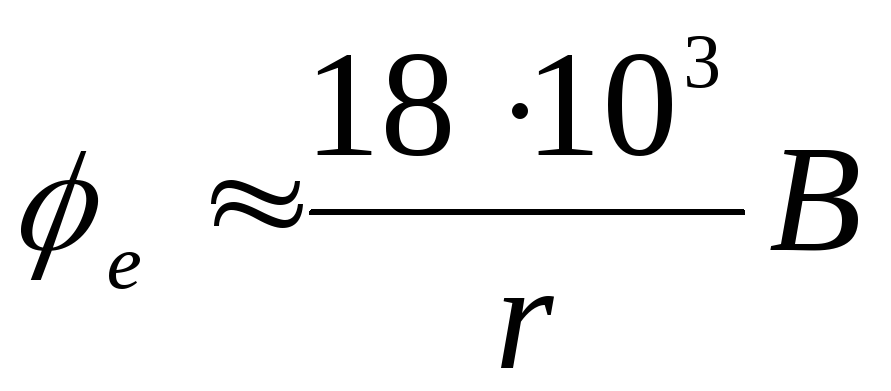 .
.
|
| |||||||
|
|
|
|
|
|
|
|
|
Tagad mēs veidojam grafiku 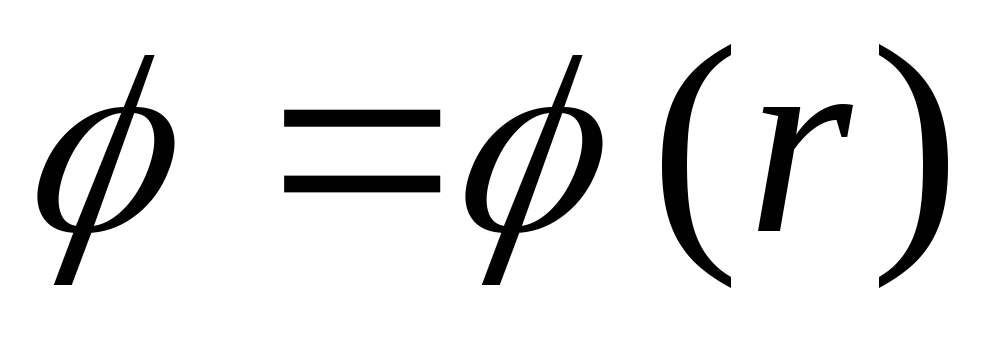 .
.
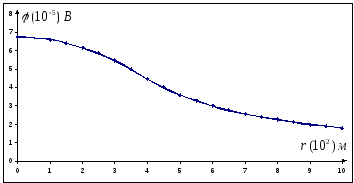
Saikne starp spriedzi un potenciālu.
Elektrostatiskā lauka stipruma atkarībai no attāluma līdz lodītes centram lodes iekšpusē ir forma (sk. 1.5.4. uzdevuma risinājumu)
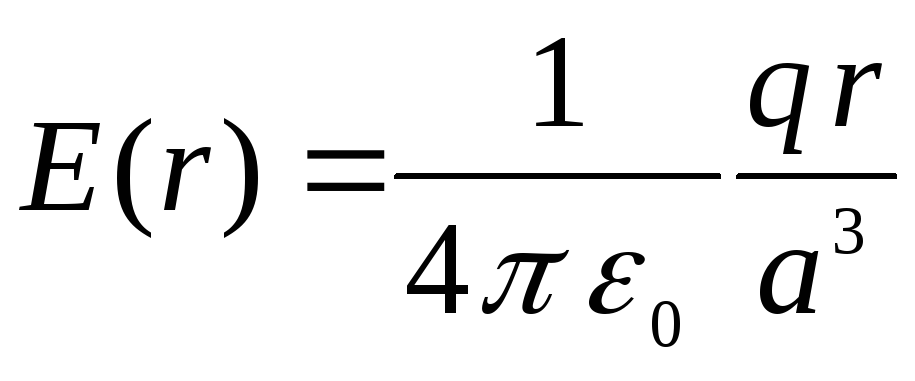 ,
,
tie. sfēras iekšpusē lauka stiprums lineāri palielinās līdz ar attālumu no centra. Plkst 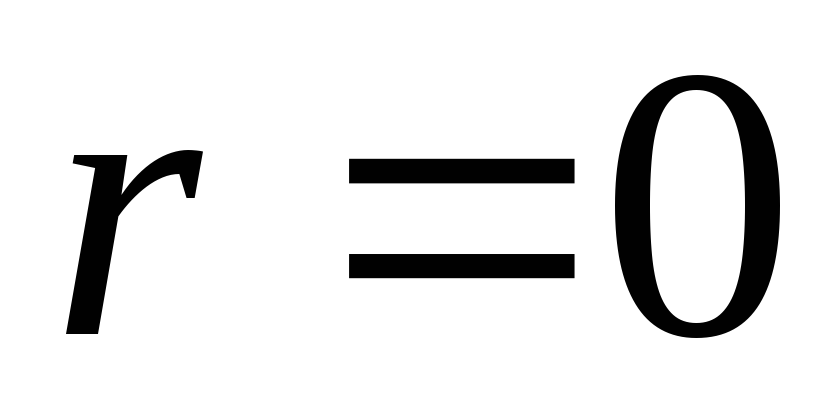 ,
,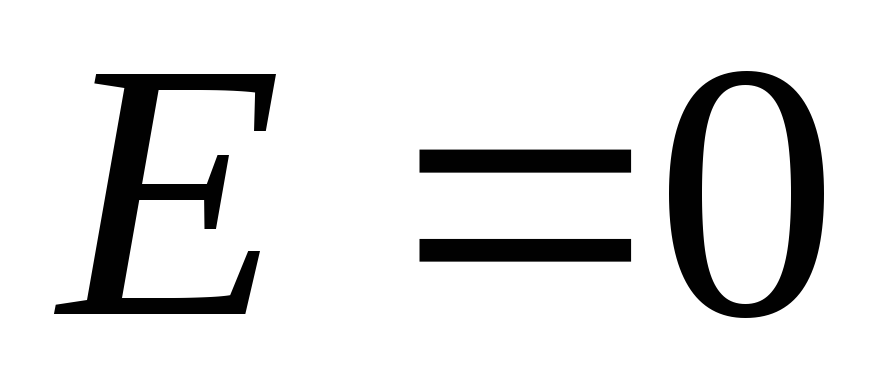 , plkst
, plkst 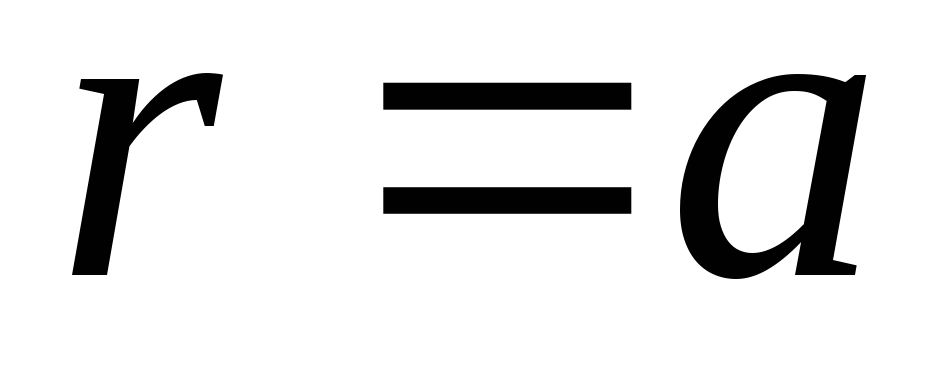 tas sasniedz maksimumu un kļūst vienāds ar
tas sasniedz maksimumu un kļūst vienāds ar
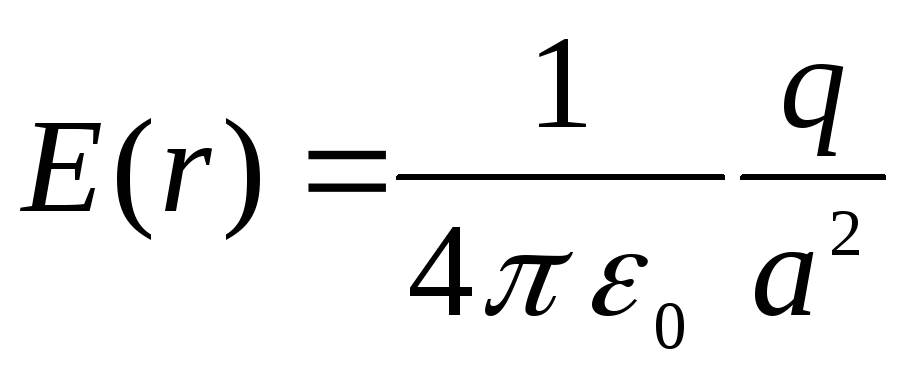 .
.
Plkst  lauka stiprums ir atkarīgs no attāluma kā punktveida lādiņa lauka stiprums.
lauka stiprums ir atkarīgs no attāluma kā punktveida lādiņa lauka stiprums.
Iespējamas izmaiņas uzlādētas bumbas laukā
Lauka potenciāls bumbas iekšpusē
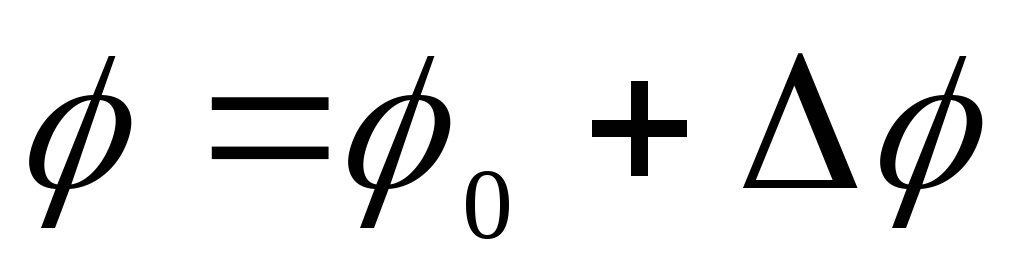 ,
,
kur 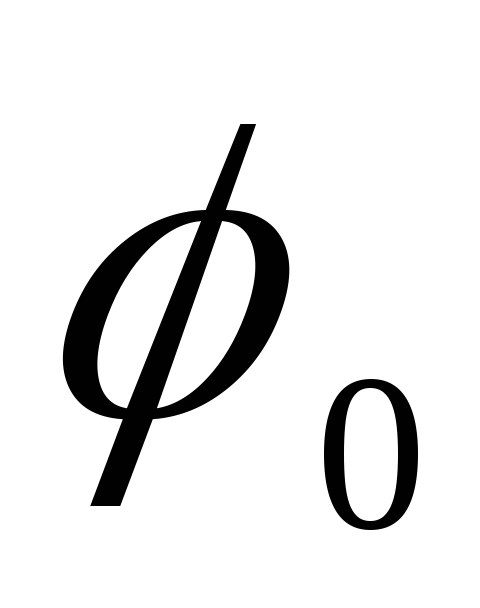 ir punkta potenciāls uz lodītes virsmas (punktveida lādiņa lauka potenciāls), vienāds ar
ir punkta potenciāls uz lodītes virsmas (punktveida lādiņa lauka potenciāls), vienāds ar
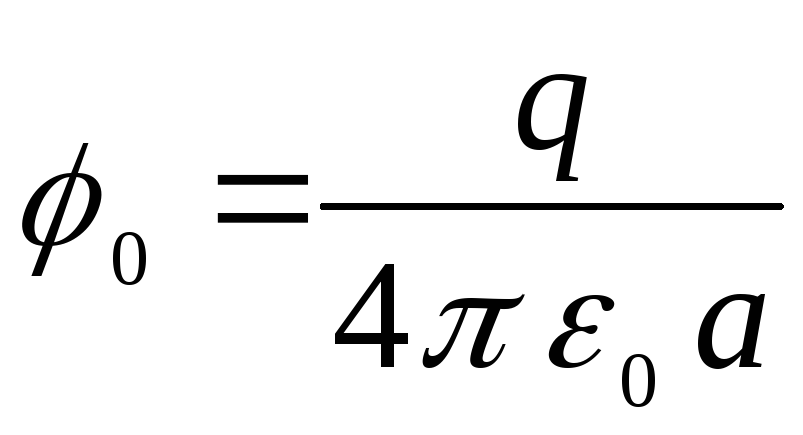 .
.
Beidzot saņemam
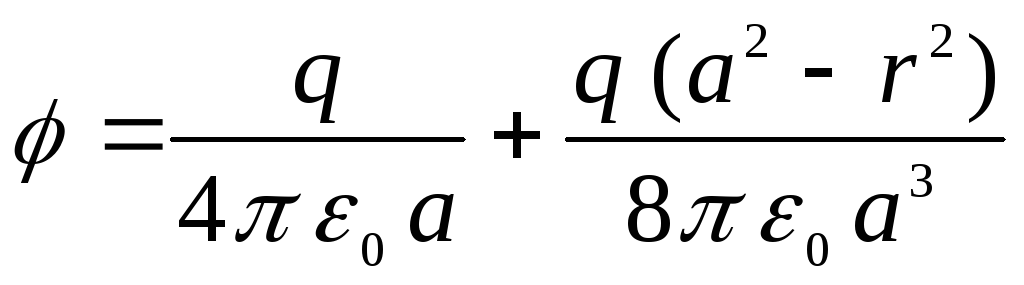 .
.
Ņemot vērā, ka tilpuma lādiņa blīvums
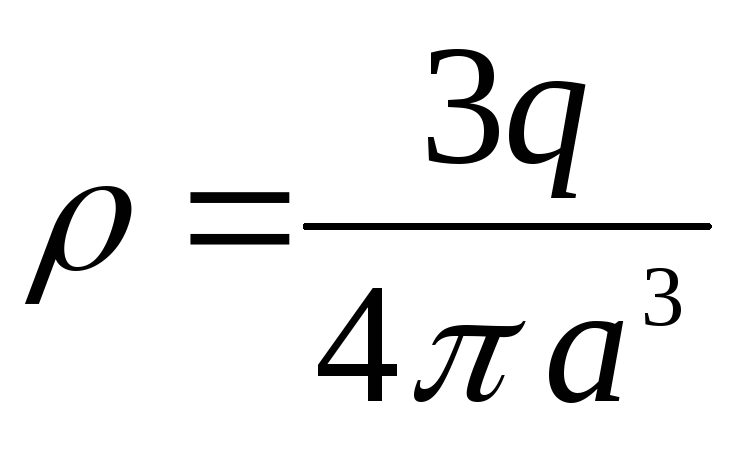 ,
,
var uzrakstīt
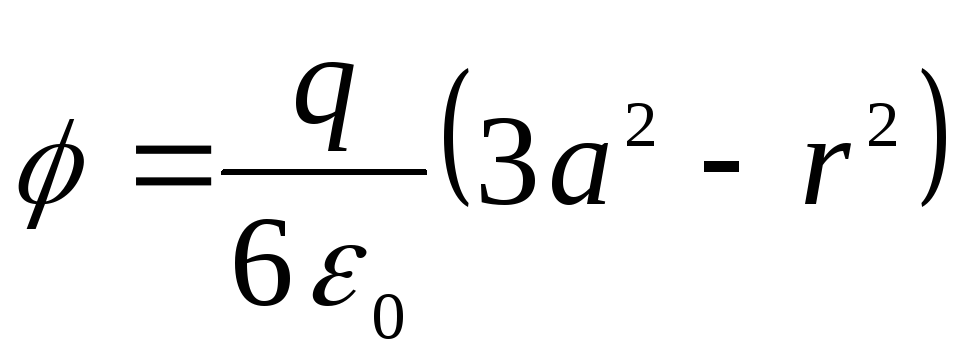 ,
,
tie. esam nonākuši pie tādas pašas formulas kā problēmas risināšanā, integrējot Puasona vienādojumu.
1.7.6. Iegūtā lauka potenciāls punktā A
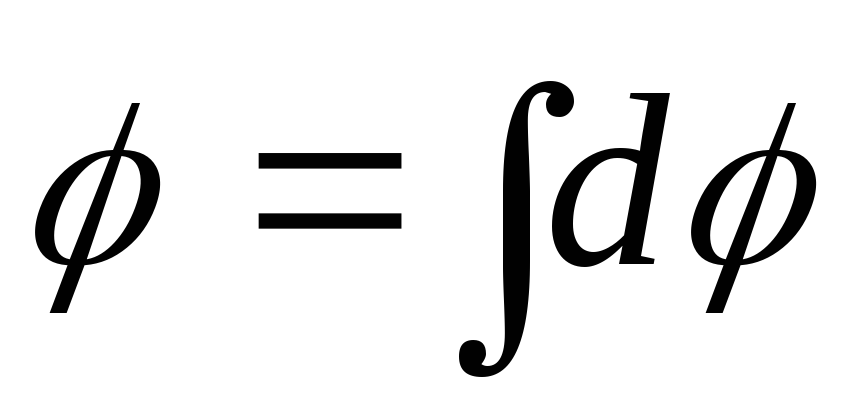 ,
,
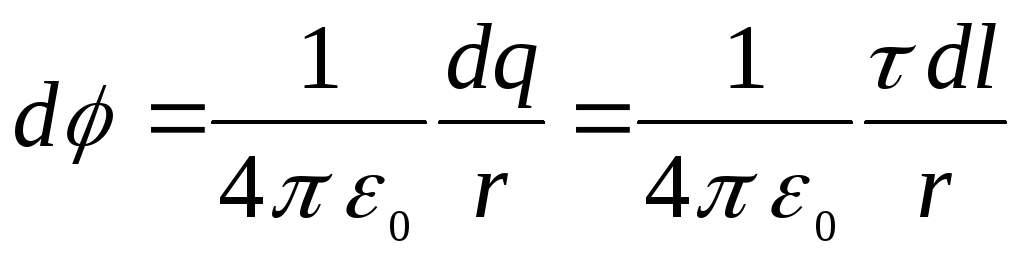
ir lādiņa radītā lauka potenciāls 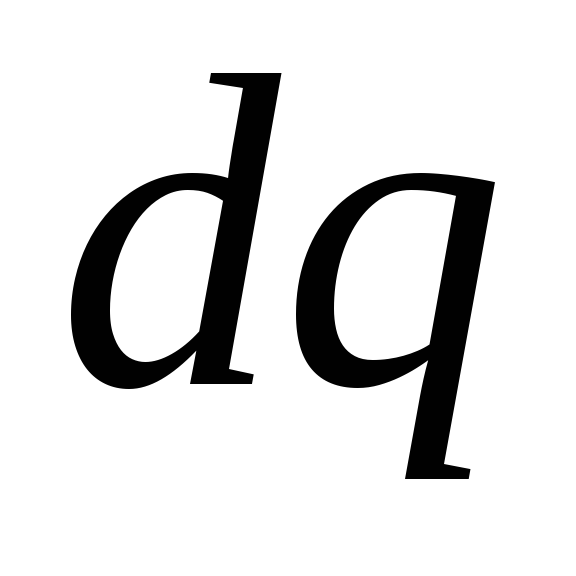 gredzena elements
gredzena elements  .
.
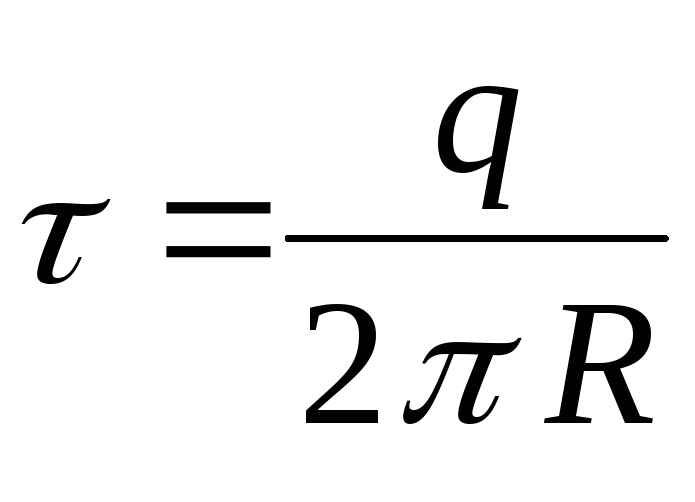
ir lineārais lādiņa blīvums, r ir attālums no elementa  uz norādīto punktu. No pēdējām divām mūsu formulām
uz norādīto punktu. No pēdējām divām mūsu formulām
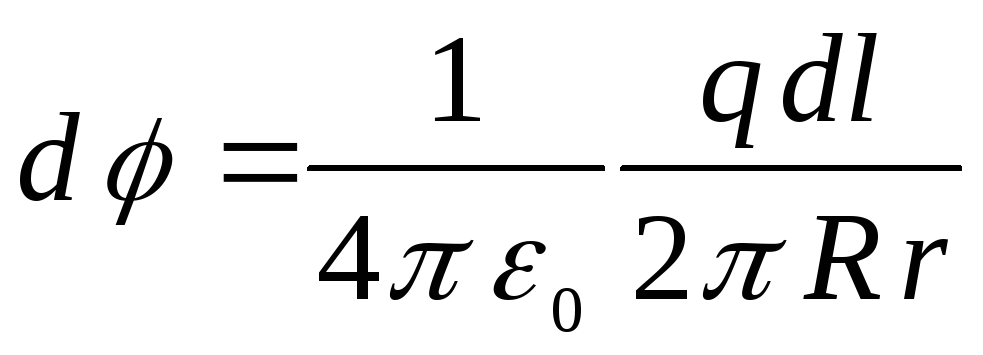 .
.
Iegūtais potenciāls
No ģeometriskiem apsvērumiem izriet, ka
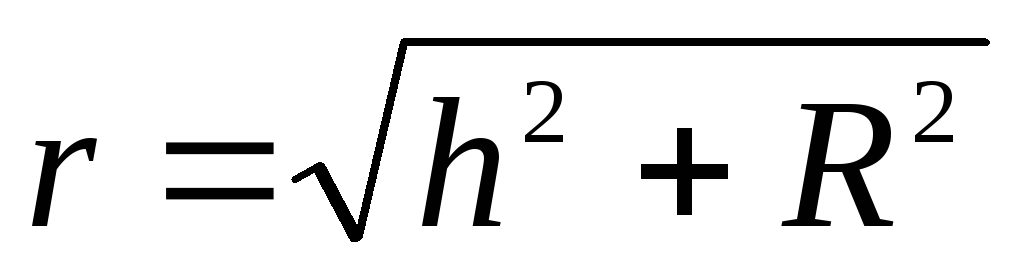 .
.
Sekojoši,
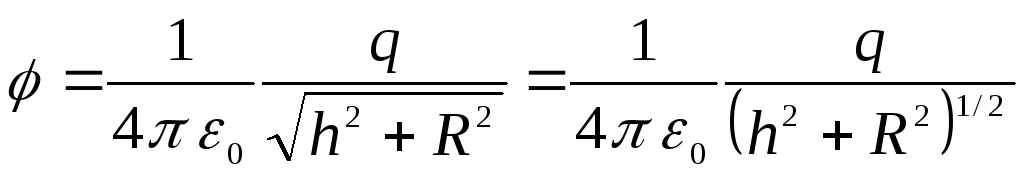 .
.
Lauka stiprums
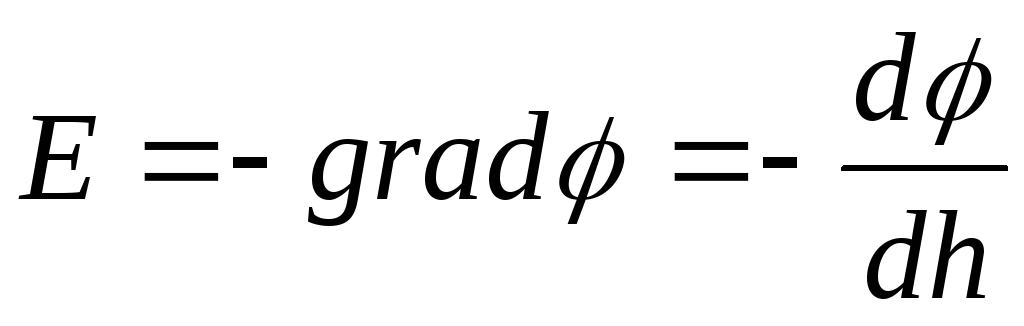 .
.
Izteiksmes parsēšana 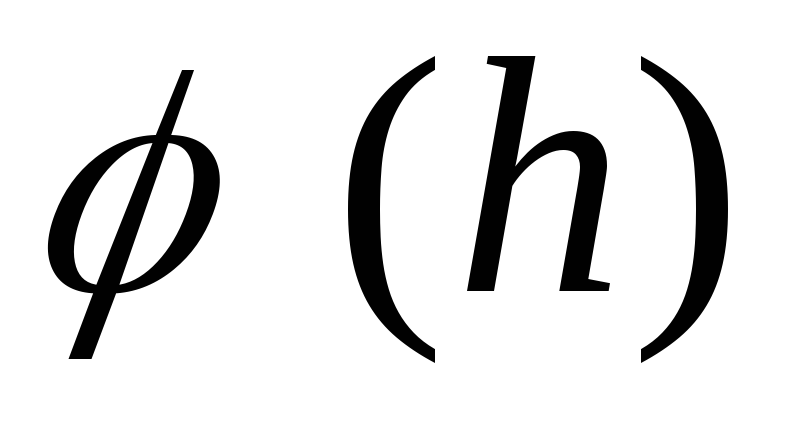 un
un ![]() parāda, ka gredzena centrā (
parāda, ka gredzena centrā ( 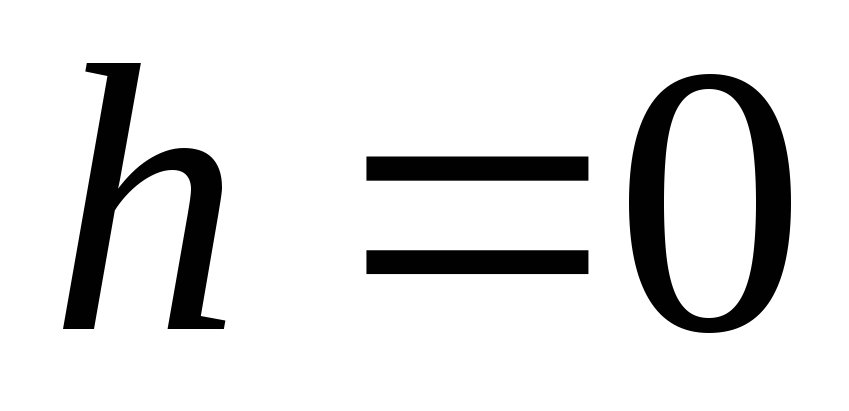 ) potenciālam ir maksimālā vērtība, un lauka stiprums pazūd.
) potenciālam ir maksimālā vērtība, un lauka stiprums pazūd.
Plkst 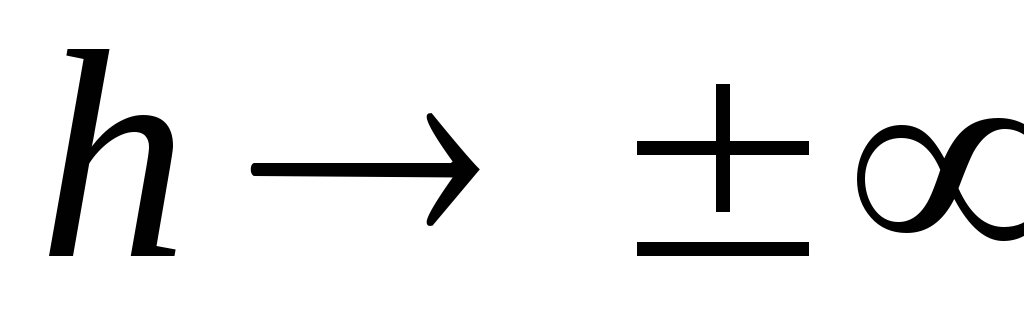 gan potenciāls, gan spriedze tiecas uz nulli.
gan potenciāls, gan spriedze tiecas uz nulli.
Plkst 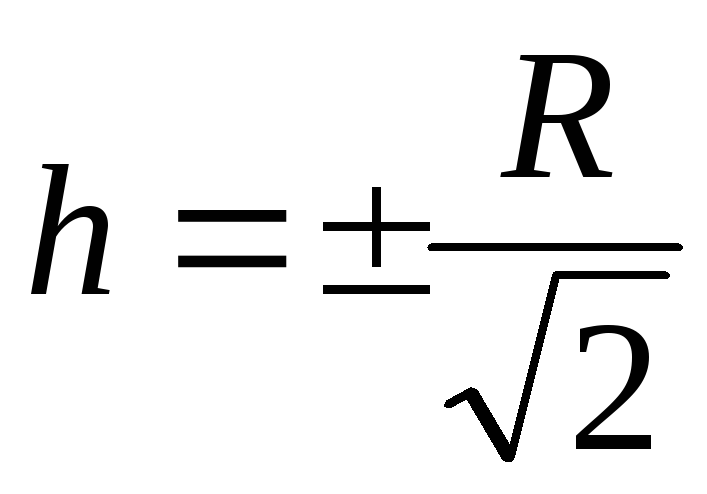 atvasinājums
atvasinājums 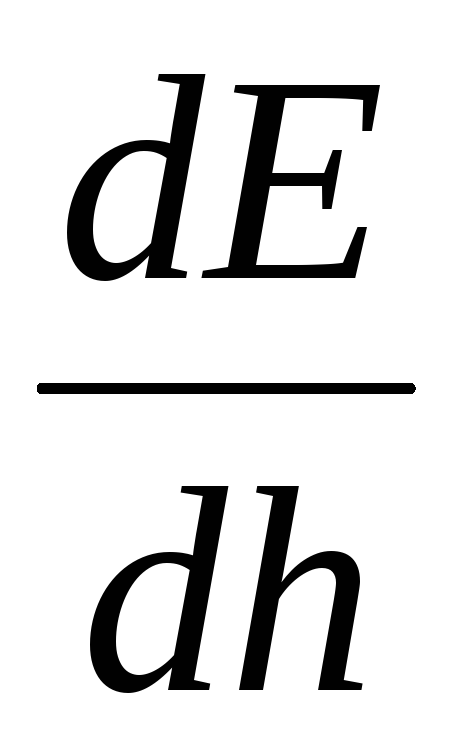 pazūd, tāpēc šajā brīdī lauka stiprums ir maksimālais, un grafikā
pazūd, tāpēc šajā brīdī lauka stiprums ir maksimālais, un grafikā 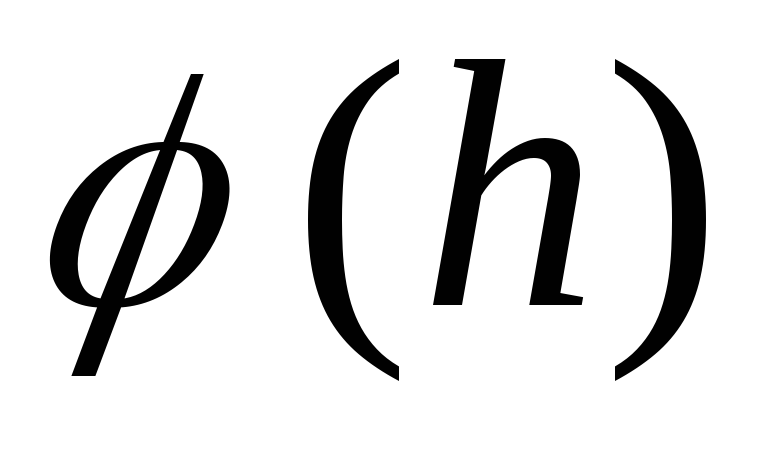 (skat. att. ____) būs lēciena punkts. Grafiks
(skat. att. ____) būs lēciena punkts. Grafiks ![]() atrodas 1. un 3. ceturksnī, t.i.
atrodas 1. un 3. ceturksnī, t.i. 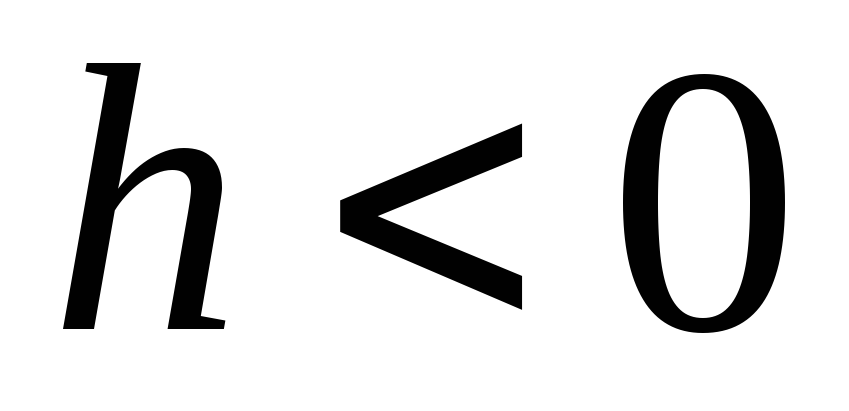 ,
,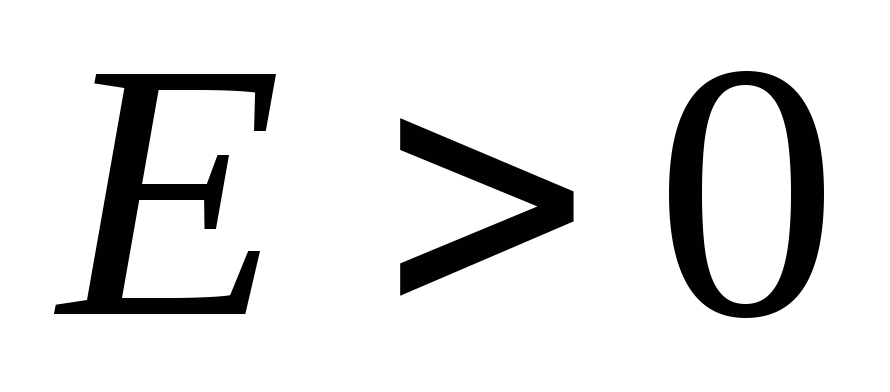 . Tas nozīmē, ka, izejot cauri gredzena centram (
. Tas nozīmē, ka, izejot cauri gredzena centram ( 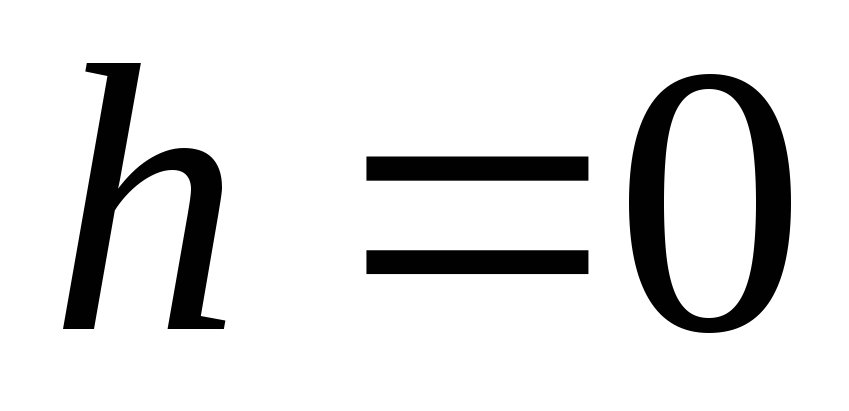 ) vektors
) vektors  maina virzienu uz pretējo.
maina virzienu uz pretējo.
Grafiks 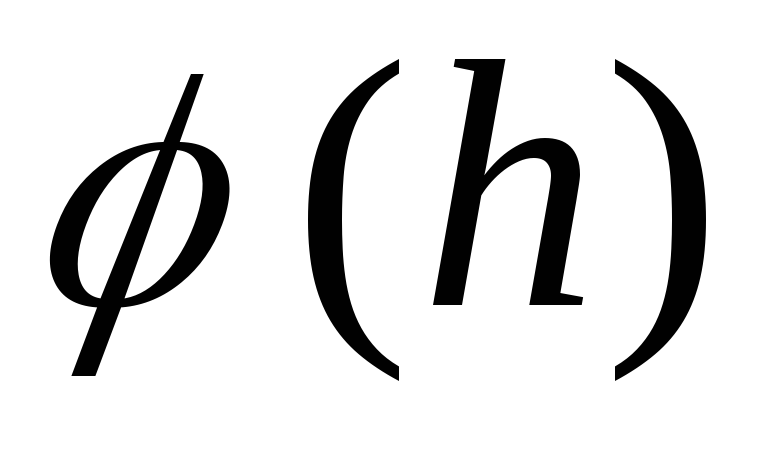 atrodas 1. un 2. ceturksnī, t.i. abās gredzena pusēs punktos, kas atrodas uz tā ass, potenciāls ir pozitīvs.
atrodas 1. un 2. ceturksnī, t.i. abās gredzena pusēs punktos, kas atrodas uz tā ass, potenciāls ir pozitīvs.
Izmantojot šīs problēmas risināšanas piemēru, var pārliecināties, ka, mainot potenciālo atskaiti, potenciālā starpība starp jebkuriem diviem punktiem nemainās. Nemainās arī viss potenciāla atkarības no attāluma raksturs. Piemēram, ja izvēlaties izcelsmi gredzena centrā, t.i. pieņemot, ka 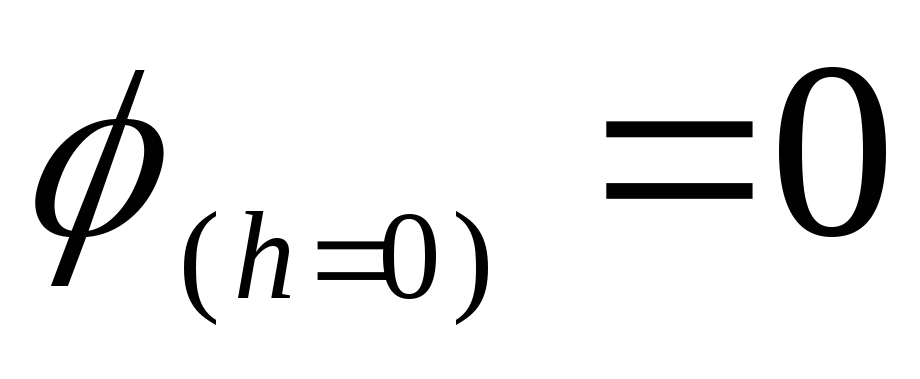 , tad jebkura punkta, kas atrodas uz gredzena ass, potenciāls ir vienāds ar
, tad jebkura punkta, kas atrodas uz gredzena ass, potenciāls ir vienāds ar
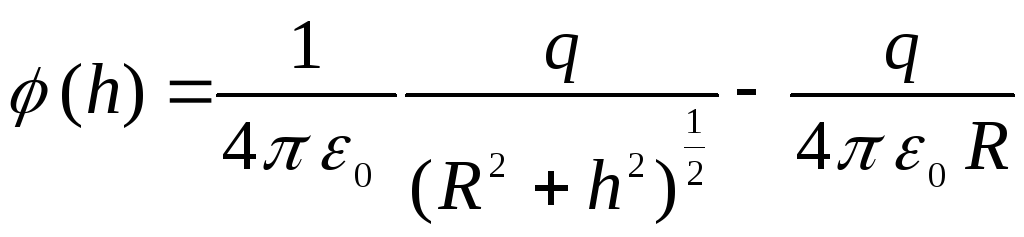 .
.
Šo formulu var viegli iegūt, pamatojoties uz superpozīcijas principu.
Ja potenciāla izcelsmi izvēlas gredzena centrā, tad elementārā lādiņa radītā lauka potenciālu 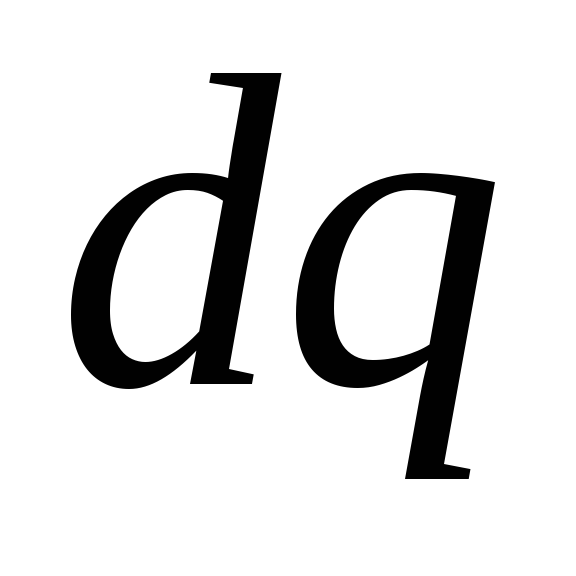 punktā A, var attēlot kā
punktā A, var attēlot kā
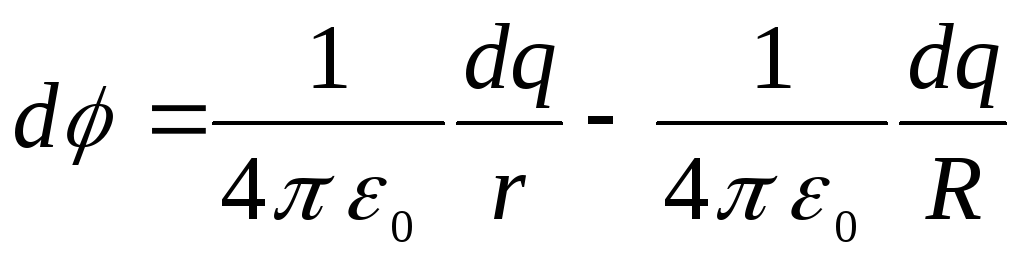 .
.
Integrējot šo izteiksmi visā gredzenā, mēs iegūstam formulu
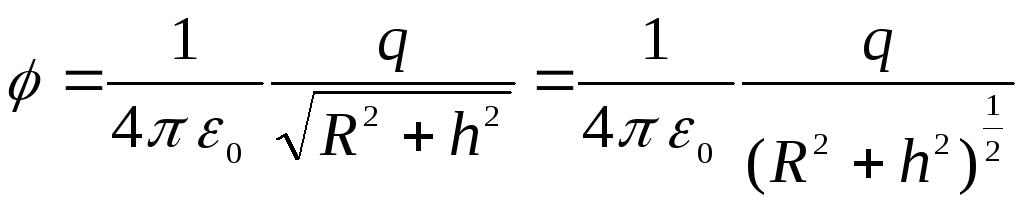 .
.
atkarības grafiks 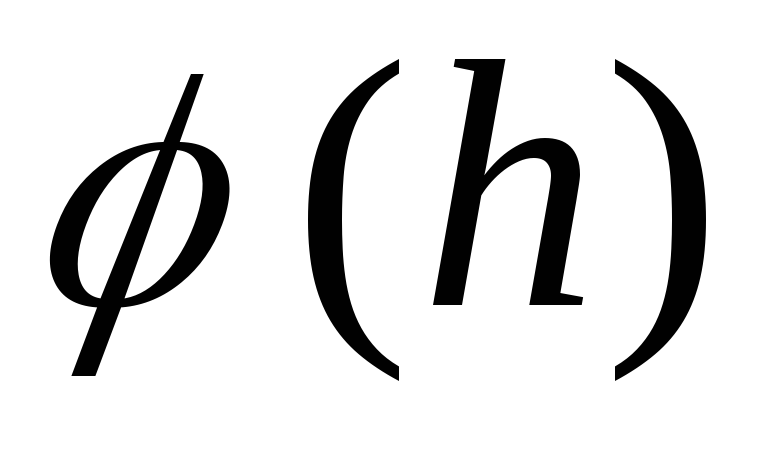 , nemainot savu raksturu, nobīdās uz leju paralēli sev par summu
, nemainot savu raksturu, nobīdās uz leju paralēli sev par summu 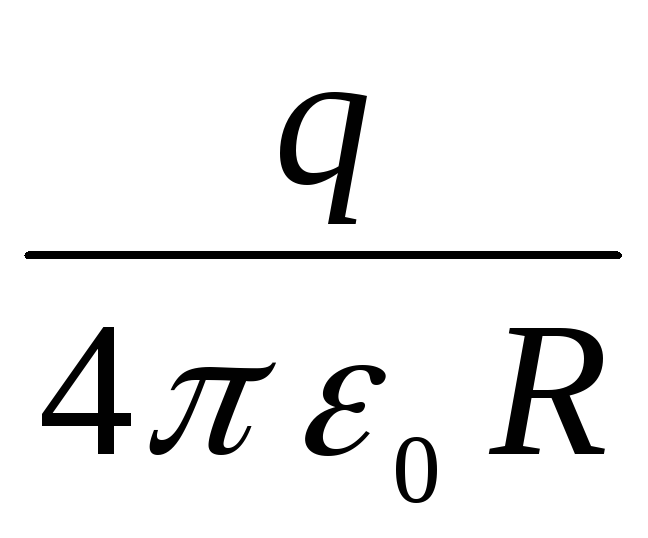 (pārtraukta līnija _____2. attēlā). Plkst
(pārtraukta līnija _____2. attēlā). Plkst 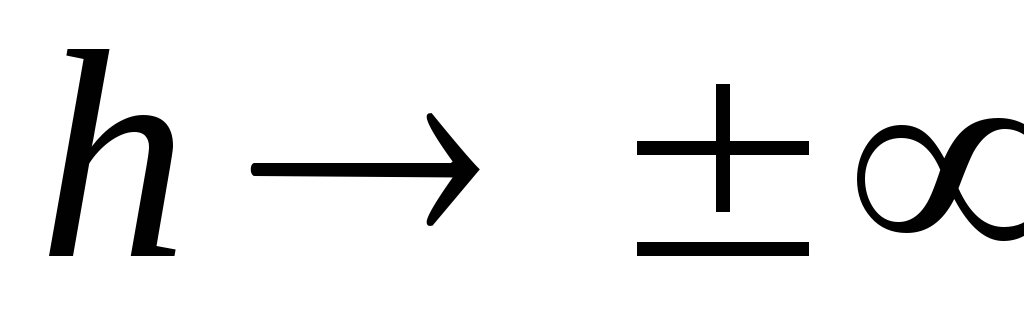 potenciāls mēdz novērtēt
potenciāls mēdz novērtēt 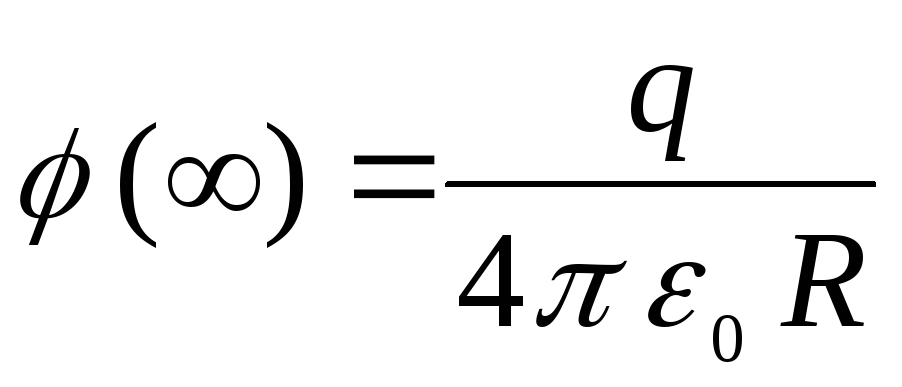 .
.
7.7. Potenciāls skaitliski līdzvērtīgs darbam, ko veic elektriskā lauka spēki, pārvietojot vienības pozitīvu lādiņu no noteiktā lauka punkta (mūsu gadījumā no iekšējās sfēras virsmas) līdz bezgalībai, t.i.
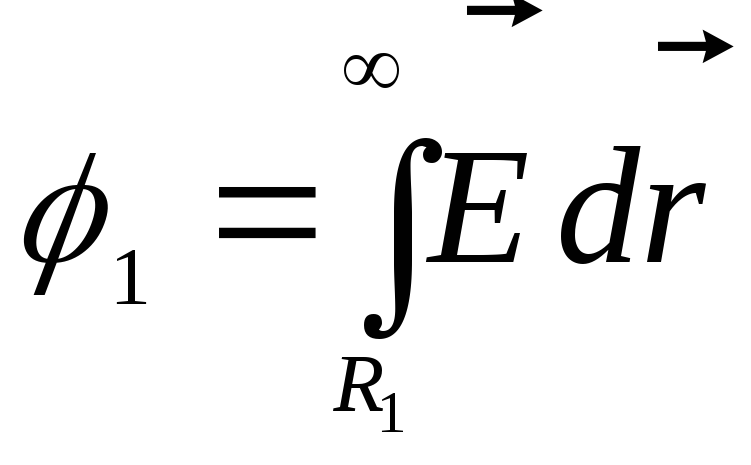 ,
,
kur  ir iegūtais lauka stiprums visos integrācijas intervāla punktos.
ir iegūtais lauka stiprums visos integrācijas intervāla punktos.
Intervālā 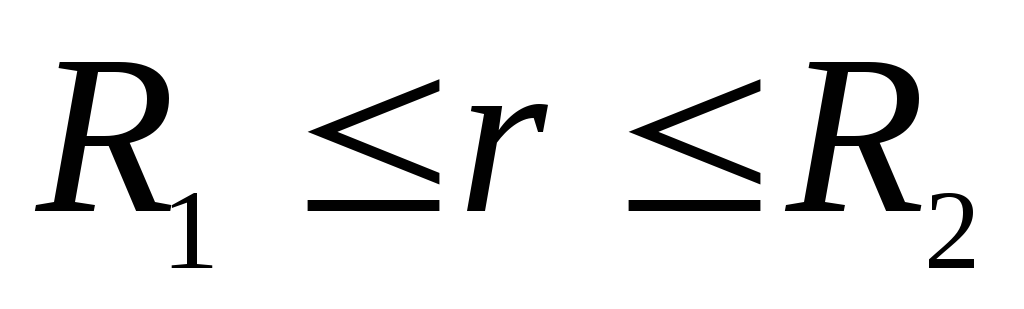 lauku rada tikai iekšējās sfēras lādiņš. Vektors
lauku rada tikai iekšējās sfēras lādiņš. Vektors  , neatkarīgi no lādiņa lieluma un zīmes
, neatkarīgi no lādiņa lieluma un zīmes 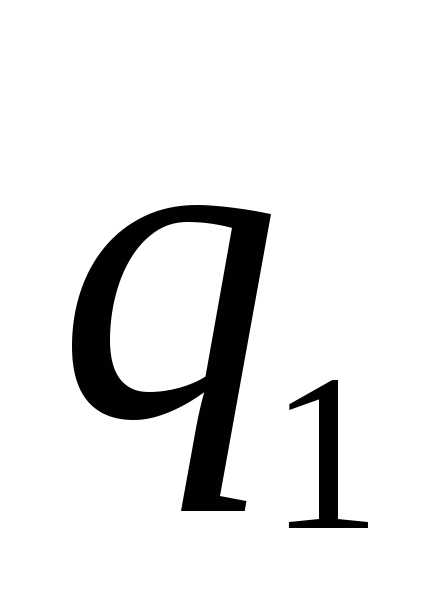 , kas vērsta pa rādiusu no centra. Pārvietojot vienību pozitīvu lādiņu no
, kas vērsta pa rādiusu no centra. Pārvietojot vienību pozitīvu lādiņu no  pirms tam
pirms tam 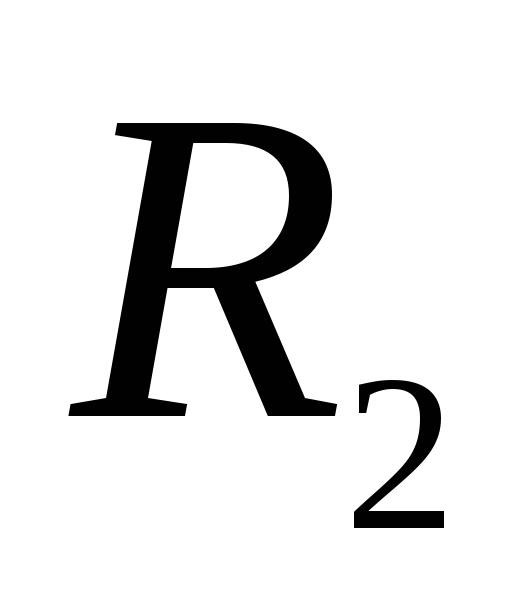 lauka spēki veic pozitīvu darbu. Plkst
lauka spēki veic pozitīvu darbu. Plkst 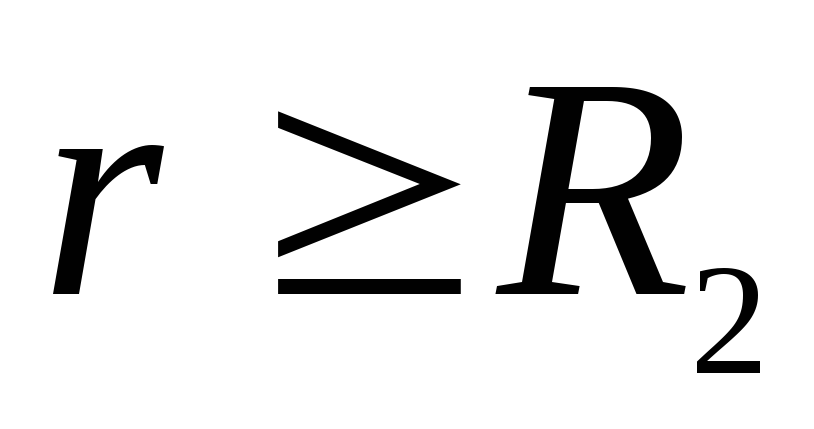 , t.i. ārpus otrās sfēras lauka spēku darbs ir negatīvs un līdz ar to vektors
, t.i. ārpus otrās sfēras lauka spēku darbs ir negatīvs un līdz ar to vektors  vērsta pa rādiusu uz sfēras centru. Punktos
vērsta pa rādiusu uz sfēras centru. Punktos 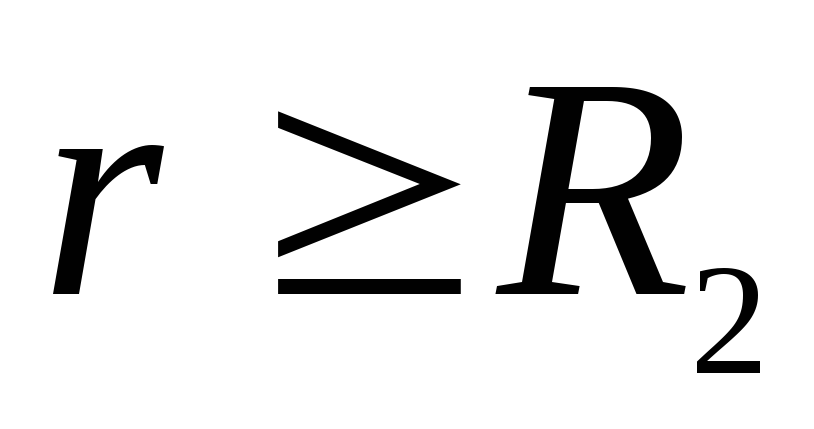 lauku nosaka abu sfēru lādiņu algebriskā summa. Uzlādē
lauku nosaka abu sfēru lādiņu algebriskā summa. Uzlādē 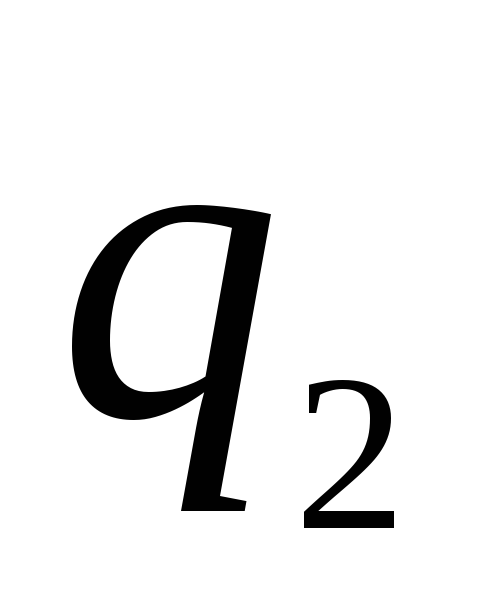 jābūt negatīvam un lielākam par lādiņu
jābūt negatīvam un lielākam par lādiņu 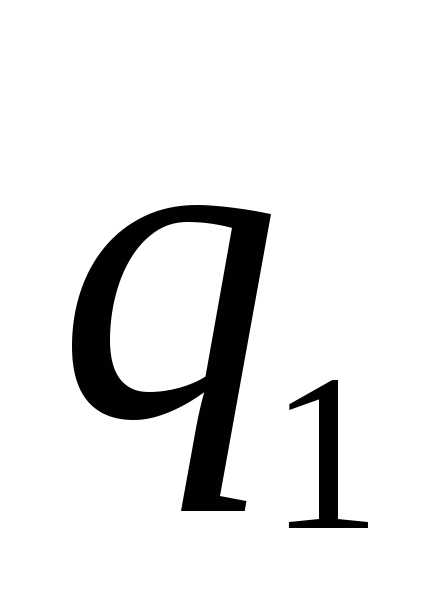 . Tā kā vektori
. Tā kā vektori  un
un 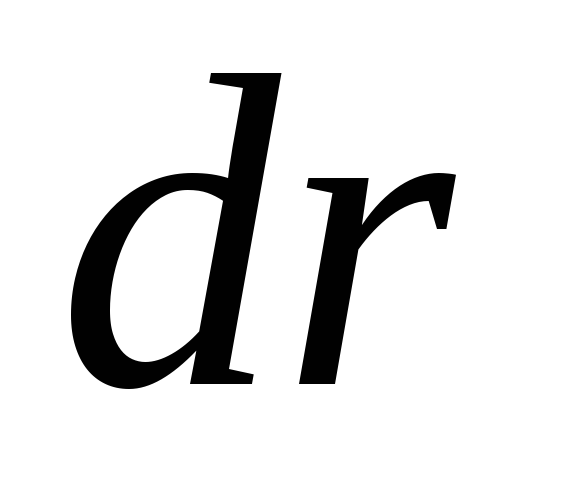 kolineārs (vai antikolineārs, ja
kolineārs (vai antikolineārs, ja 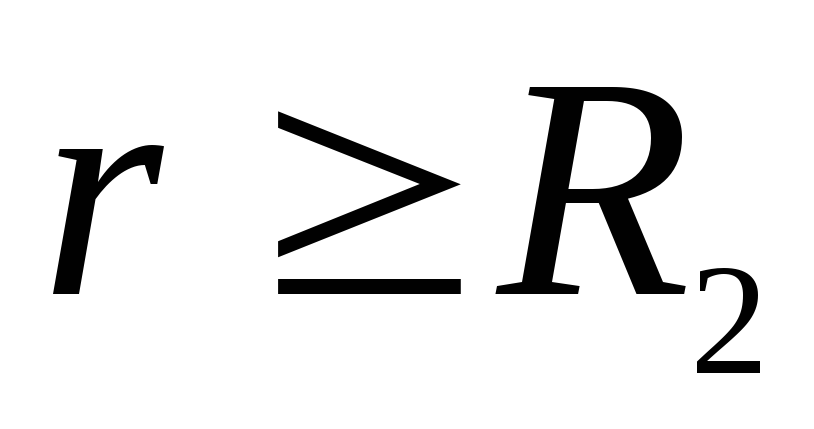 ), tad skalārais reizinājums
), tad skalārais reizinājums ![]() var aizstāt ar
var aizstāt ar 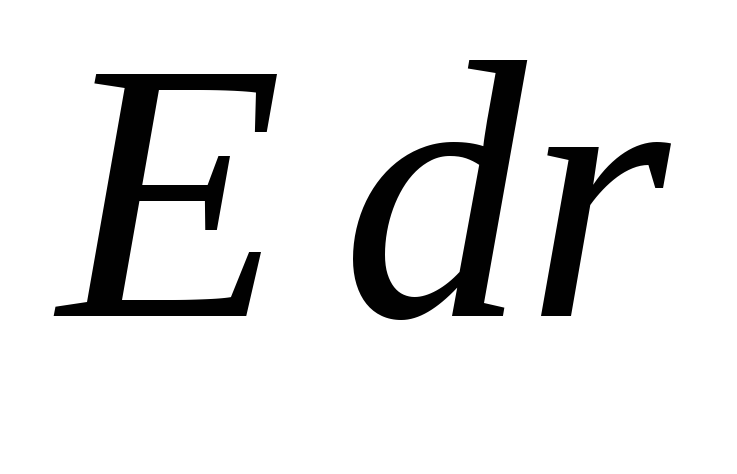 (gadījumā, ja šie divi vektori ir vērsti pretēji, lauka intensitāte jāuzskata par negatīvu). Formulā
(gadījumā, ja šie divi vektori ir vērsti pretēji, lauka intensitāte jāuzskata par negatīvu). Formulā 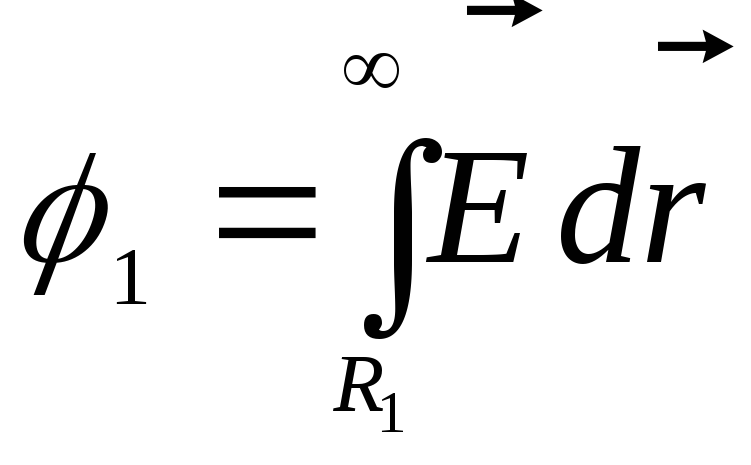 integrand
integrand 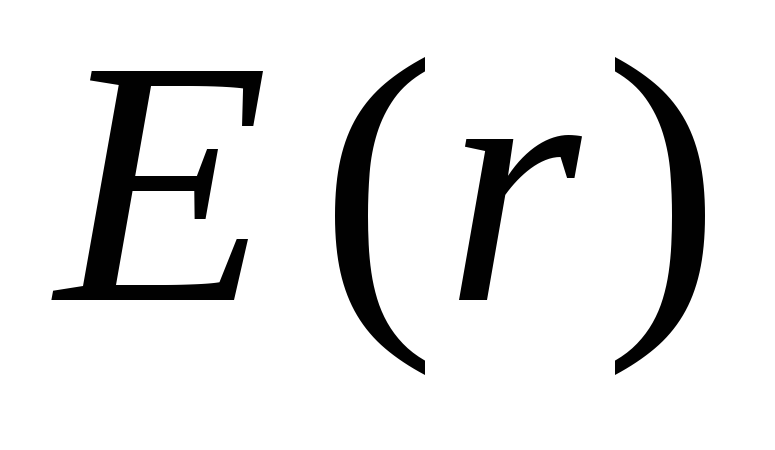 pārtraukumi kādā punktā
pārtraukumi kādā punktā 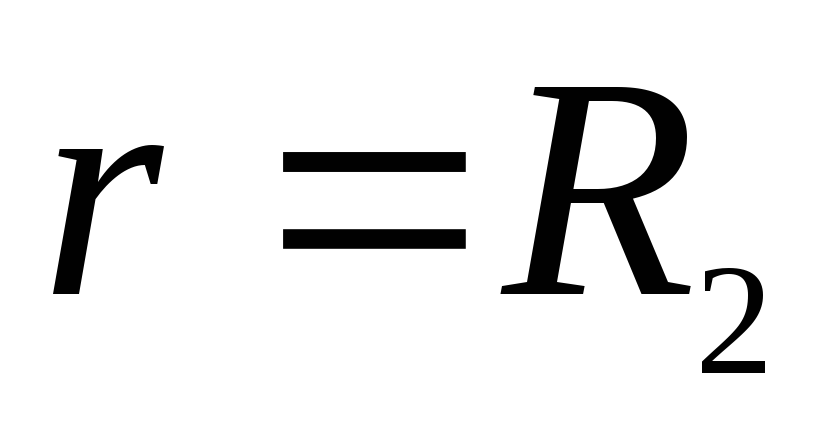 . Tāpēc integrālis ir jāsadala divos integrāļos, sākot no
. Tāpēc integrālis ir jāsadala divos integrāļos, sākot no  pirms tam
pirms tam 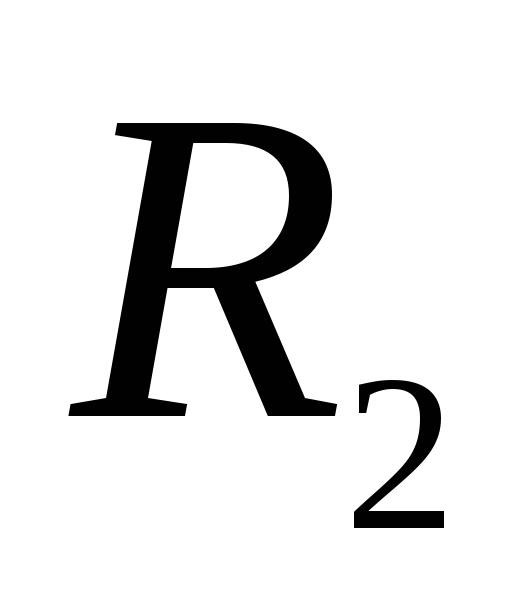 un no
un no 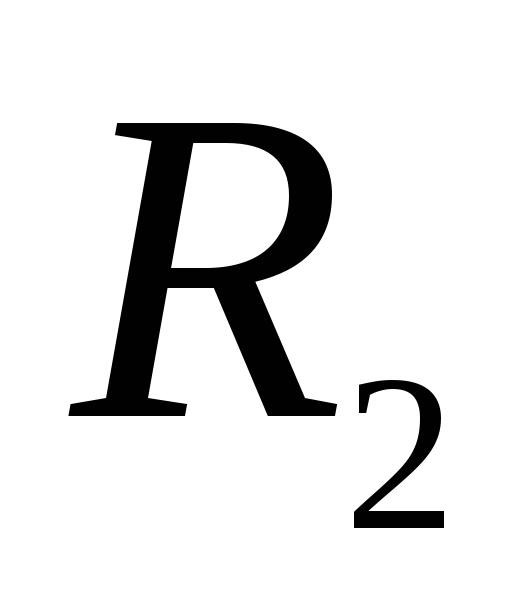 pirms tam
pirms tam  :
:
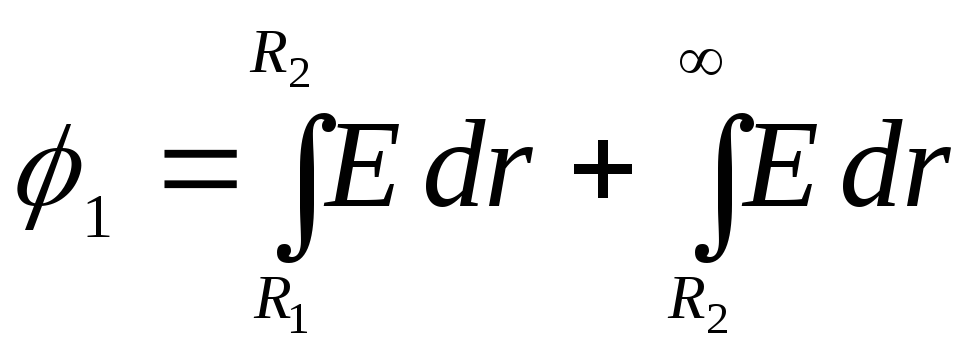 .
.
Plkst 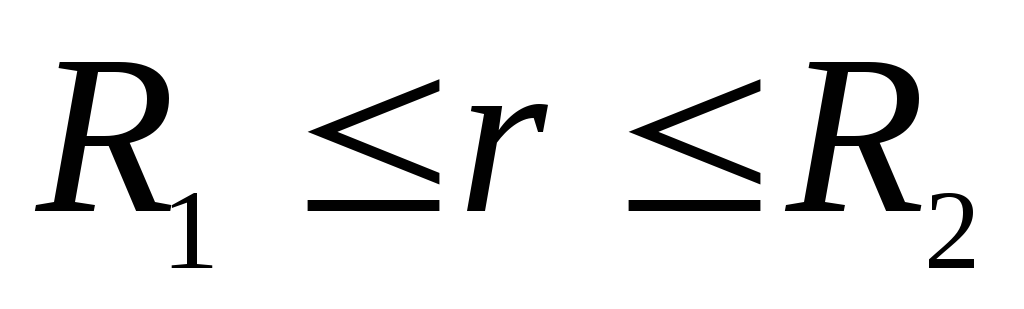 spriedze
spriedze
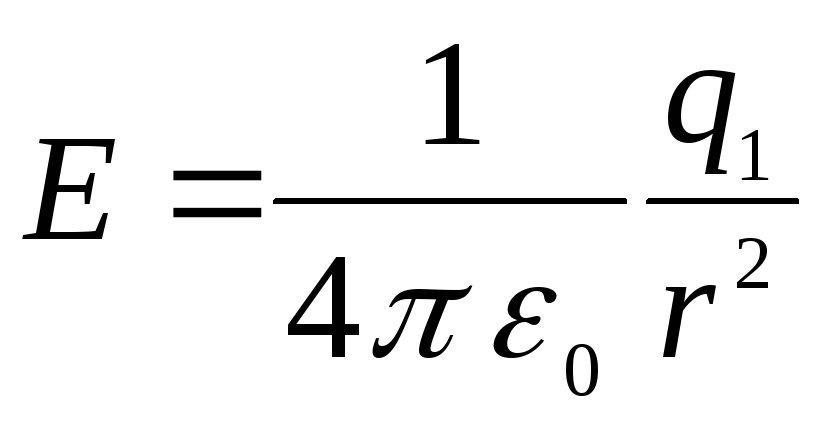 ,
,
un plkst 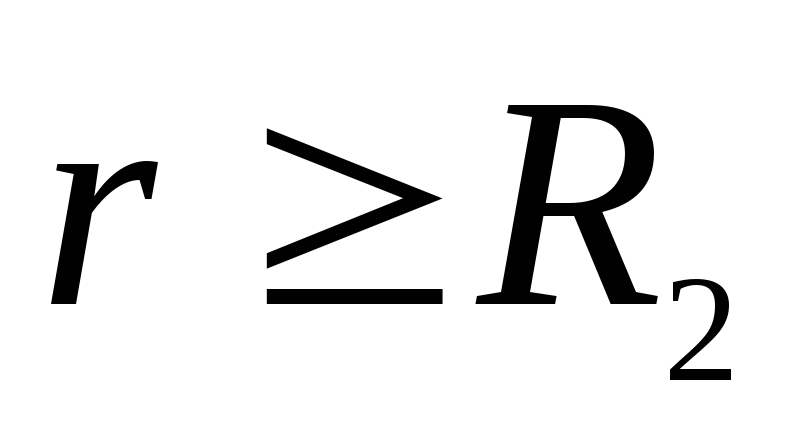
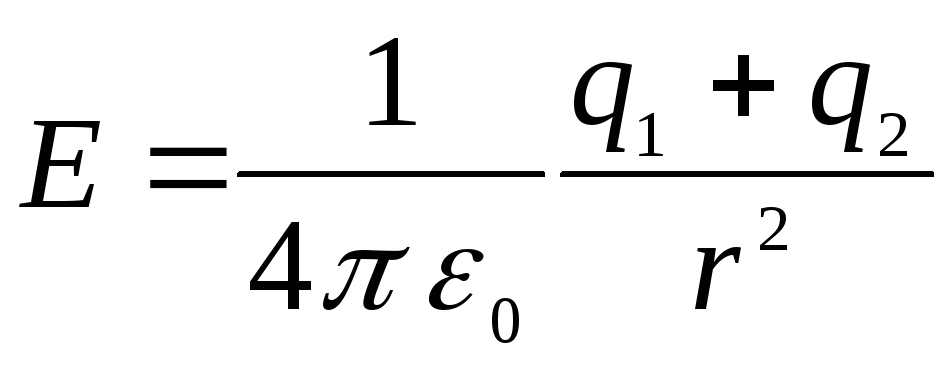 .
.
Aizvietojot šīs izteiksmes atbilstošajos integrāļos, mēs iegūstam
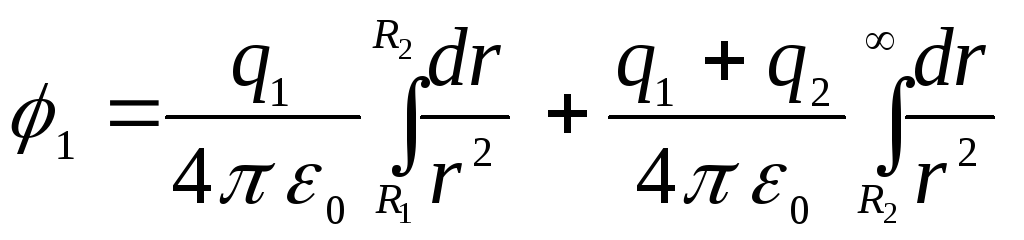 .
.
Integrējot un samazinot līdzīgus terminus, mēs iegūstam
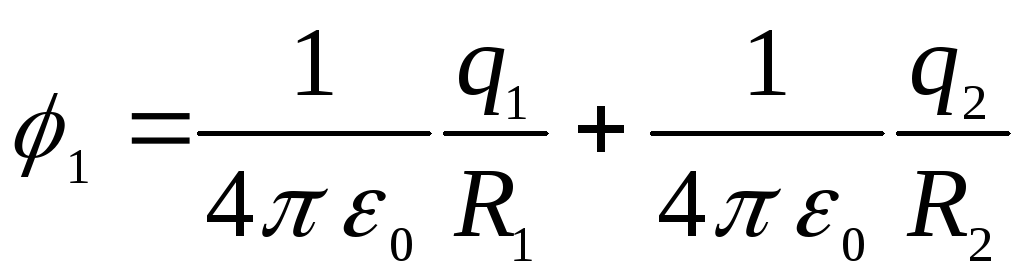 .
.
Tā kā atbilstoši problēmas stāvoklim 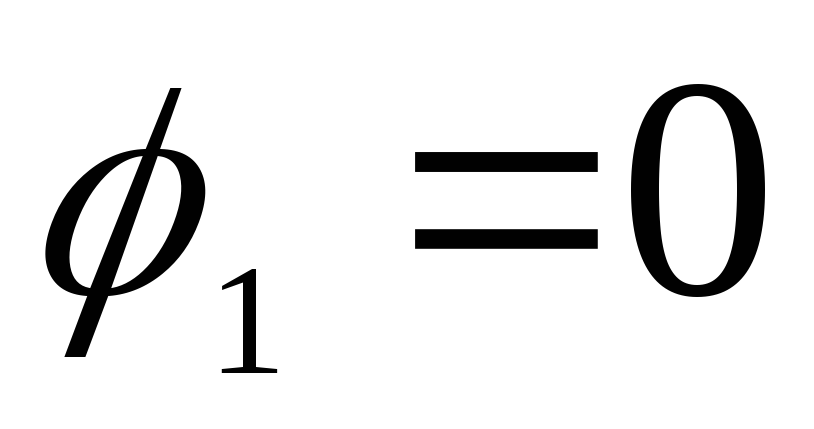 , tad
, tad
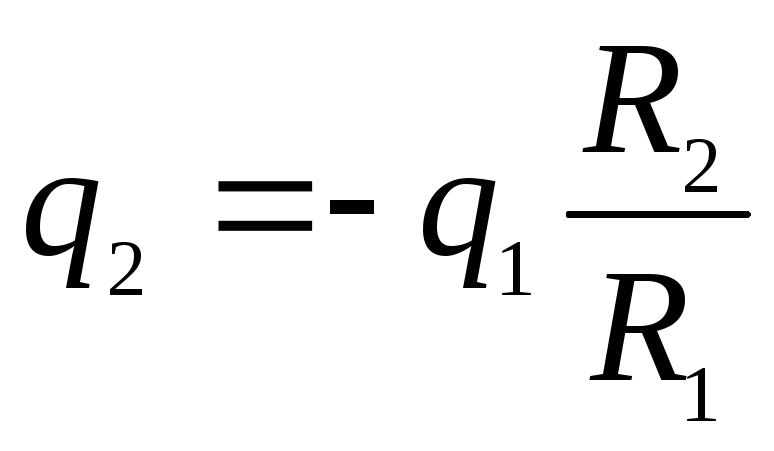 .
.
atkarības grafiks 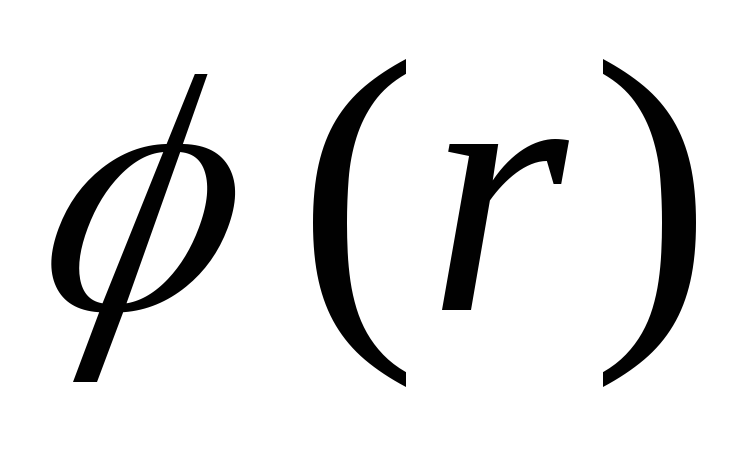 parādīts attēlā ____.
parādīts attēlā ____.
Analizēsim iegūto grafiku.
Atbilstoši problēmas stāvoklim, noteiktai vērtībai 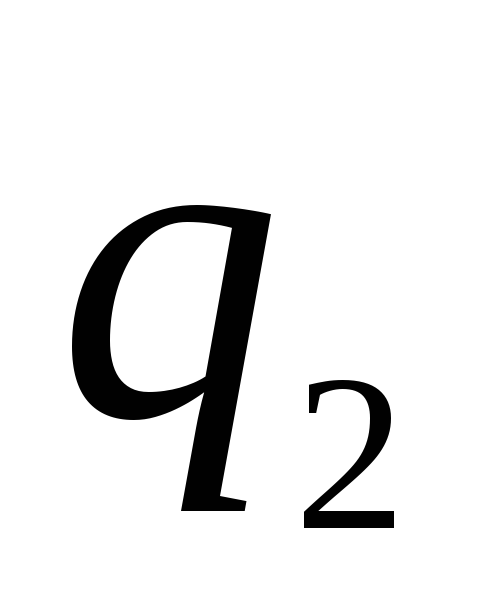 potenciāls uz iekšējās sfēras virsmas
potenciāls uz iekšējās sfēras virsmas 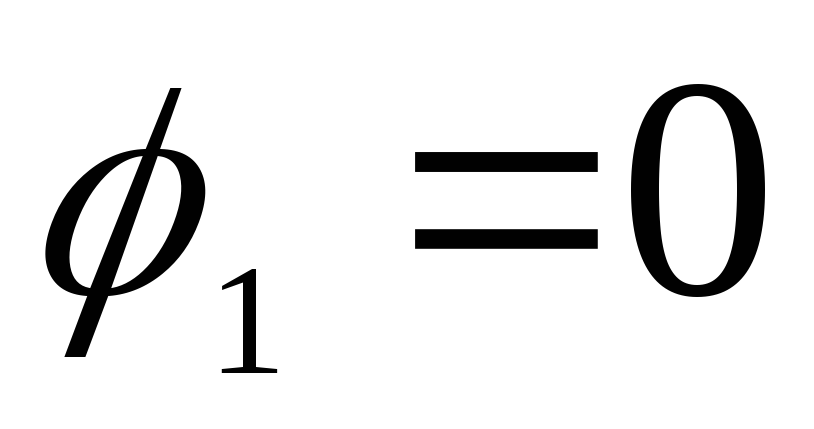 . Plkst
. Plkst 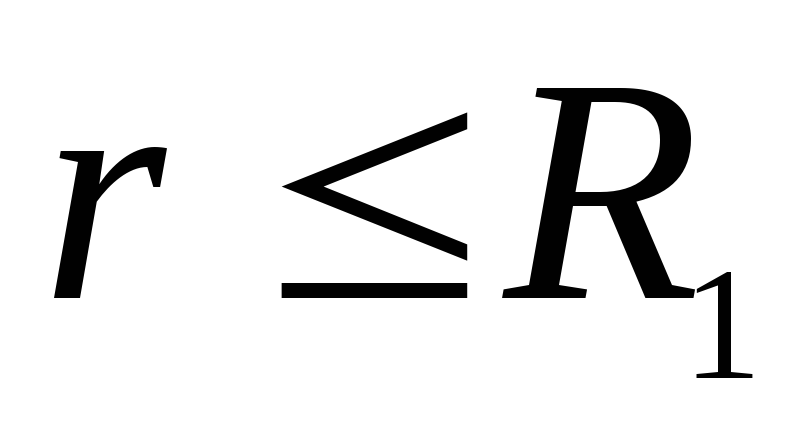 potenciāls ir nemainīgs un vienāds ar potenciālu uz virsmas, tāpēc grafiks apgabalā no
potenciāls ir nemainīgs un vienāds ar potenciālu uz virsmas, tāpēc grafiks apgabalā no 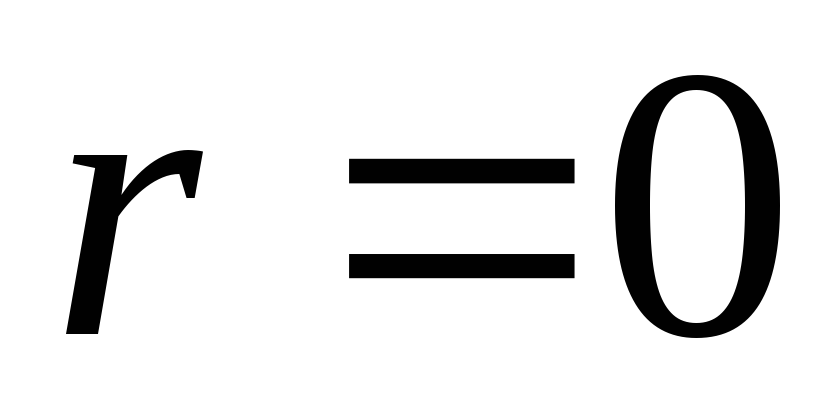 pirms tam
pirms tam 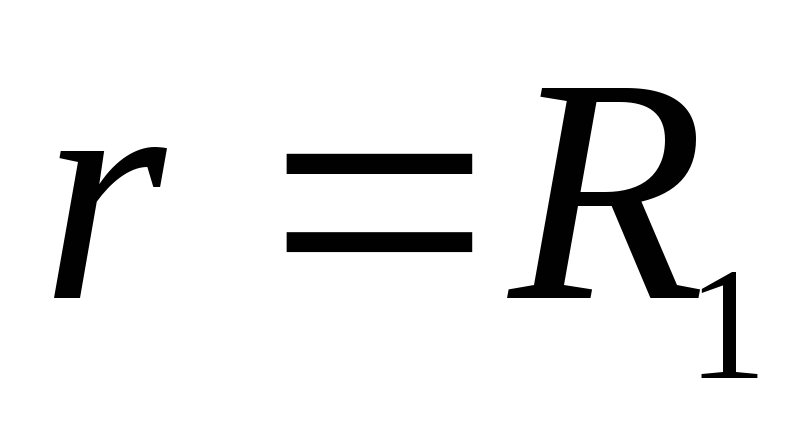 ir taisna līnija, kas sakrīt ar x asi. Plkst
ir taisna līnija, kas sakrīt ar x asi. Plkst 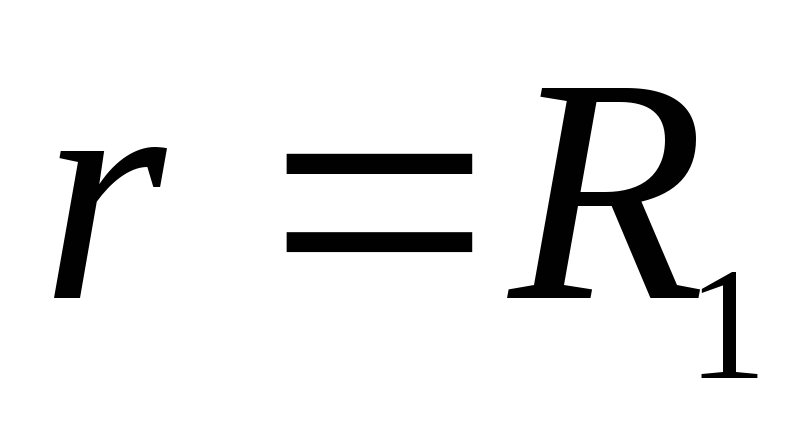 vektors
vektors  cieš pārtraukumu. Jo
cieš pārtraukumu. Jo 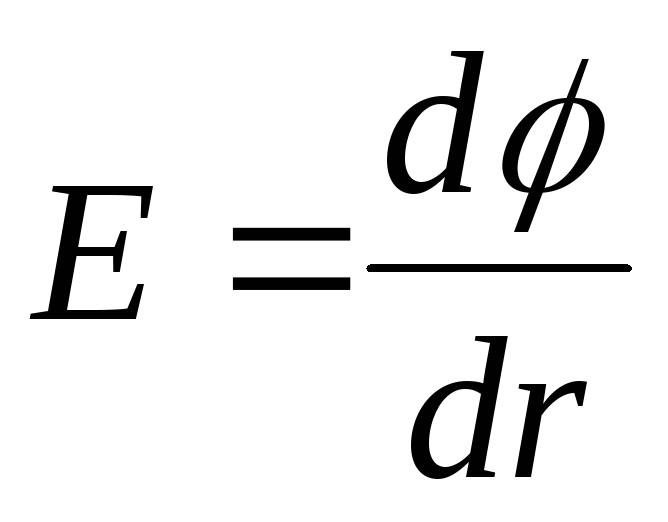 , tad grafikā punkts
, tad grafikā punkts 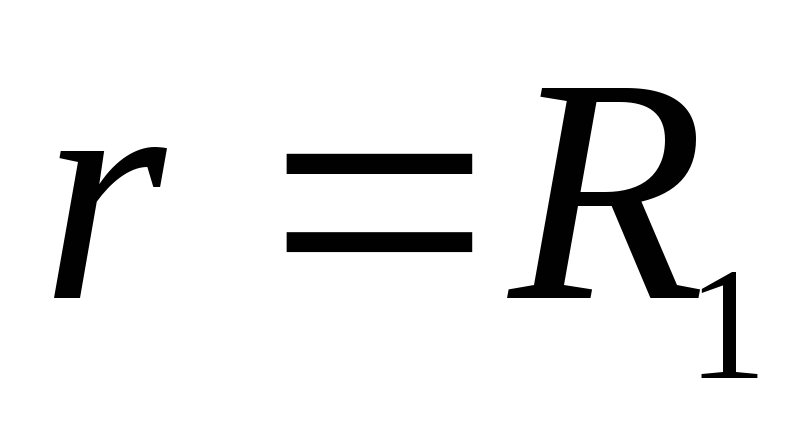 (tāds pats kā punkts
(tāds pats kā punkts 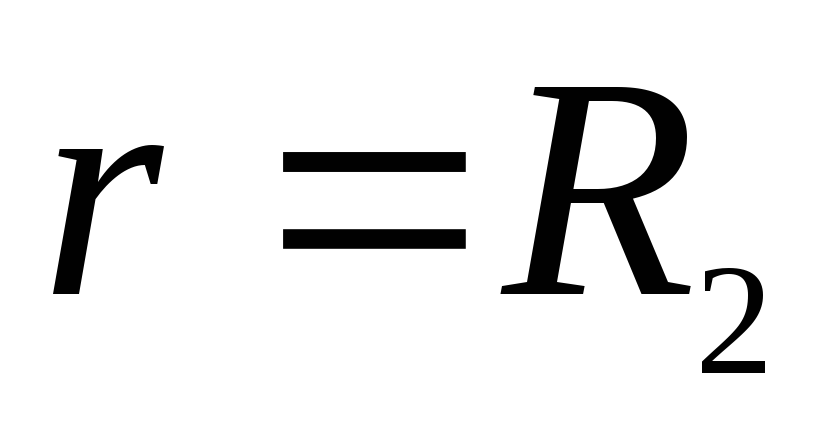 ) apzīmē vienskaitļa punktus. Atrašanās vieta ieslēgta
) apzīmē vienskaitļa punktus. Atrašanās vieta ieslēgta 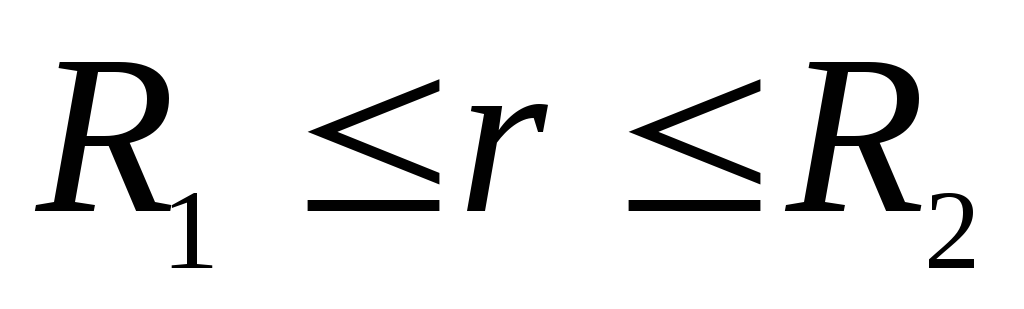 vektors
vektors  vērsta pa rādiusa vektoru
vērsta pa rādiusa vektoru 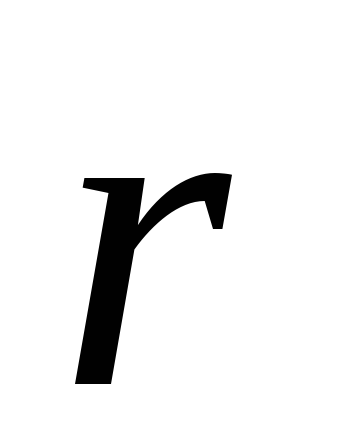 . Tāpēc, attālinoties no iekšējās sfēras virsmas, potenciāls samazinās līdz noteiktai vērtībai
. Tāpēc, attālinoties no iekšējās sfēras virsmas, potenciāls samazinās līdz noteiktai vērtībai 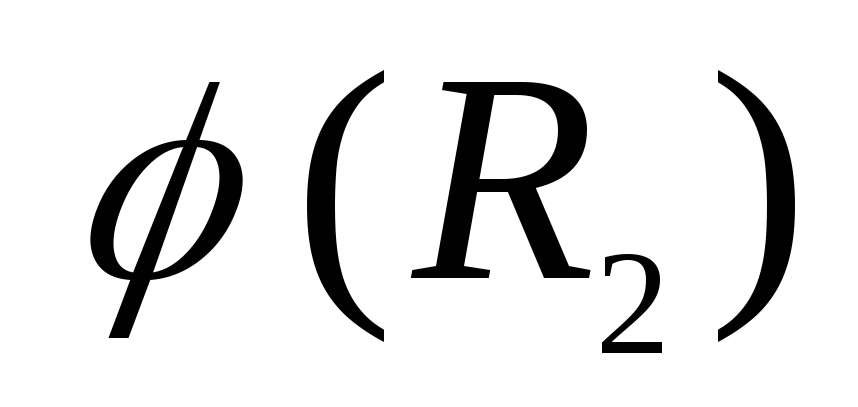 . Atrašanās vieta ieslēgta
. Atrašanās vieta ieslēgta 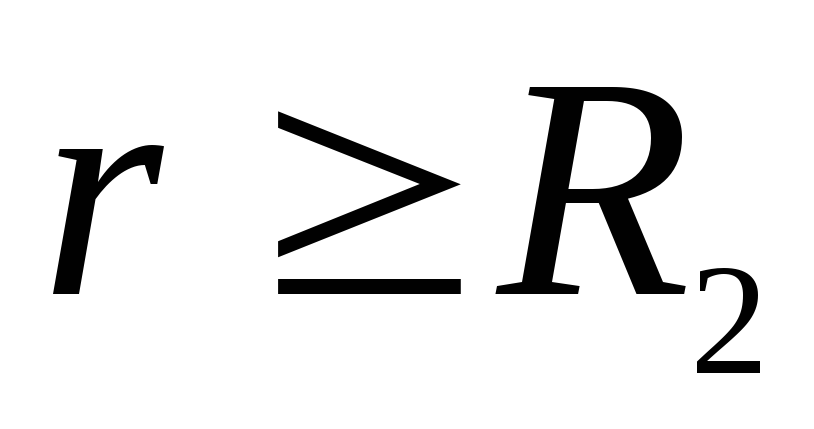 vektors
vektors  vērsta uz rādiusa vektoru
vērsta uz rādiusa vektoru 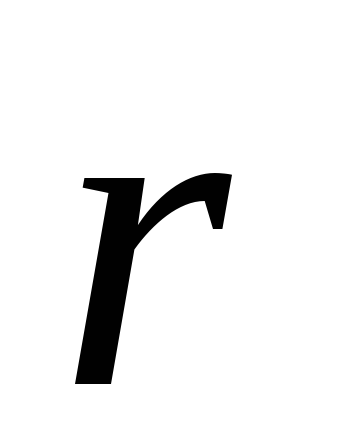 , tāpēc, palielinoties attālumam no ārējās sfēras virsmas, potenciāls palielinās, un plkst.
, tāpēc, palielinoties attālumam no ārējās sfēras virsmas, potenciāls palielinās, un plkst. 
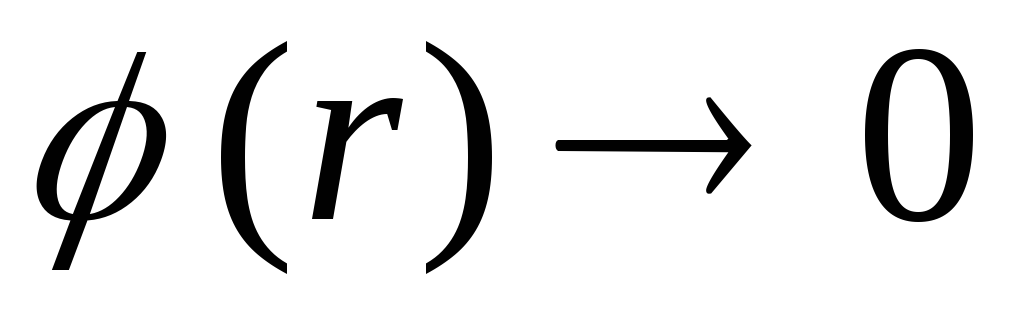 . Kaut vai punktos
. Kaut vai punktos 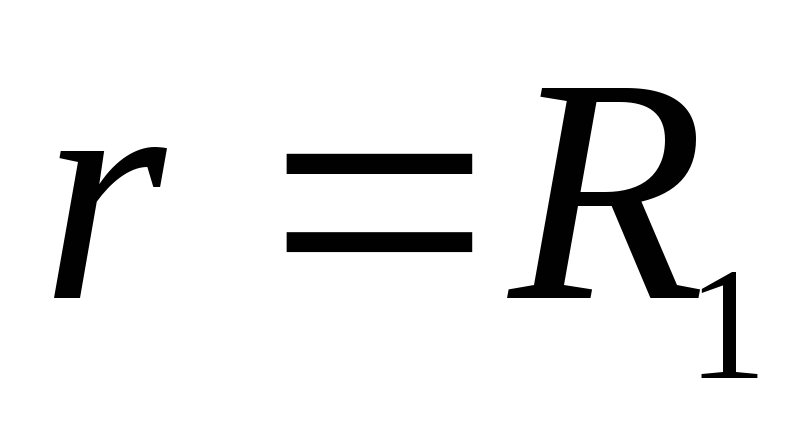 un
un 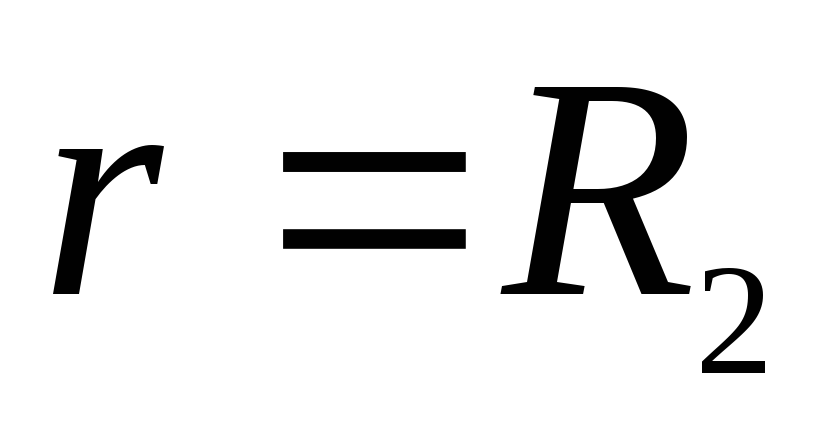 vektors
vektors  pārtraukumi, funkcija
pārtraukumi, funkcija 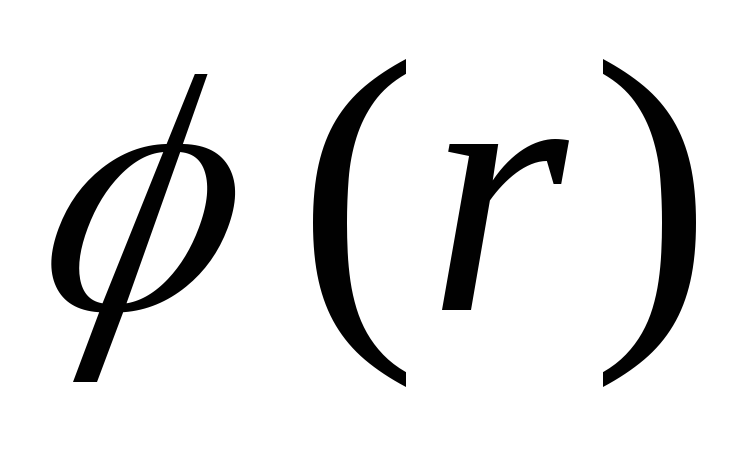 ir nepārtraukts.
ir nepārtraukts.
Starp skolas problēmām fizikā izceļas tās, kas saistītas ar koncentriskām vadošām sfērām. Šīs sfēras var uzlādēt, iezemēt, tās var būt ārējo lādiņu laukā utt., ir daudz variāciju. AT skolas kurss fizika, šīs problēmas ir vienas no visgrūtākajām. Pēdējais, bet ne mazāk svarīgais, protams, šī materiāla pārpratums ir saistīts ar skolotāju nespēju to izskaidrot kompetenti un pieejamā veidā. Tātad, mēģināsim izdomāt, kas ir šīs vadošās sfēras un ar ko tās tiek ēstas.
Iekšējās sfēras potenciāls φ 2 nosaka zināmā attiecība:
![]()
Tad kopējais potenciāls φ iekšējās sfēras virsmā ir:
Arī potenciāls uz ārējās sfēras virsmas sastāv no diviem potenciāliem: iekšējās sfēras φ’ 1 un ārējā sfēra φ’ 2 .
Iekšējās sfēras potenciāls φ’ 1 attālumā R no tā centra nosaka zināmā attiecība:
![]()
Formula, kas nosaka ārējās sfēras potenciālu φ’ 2 uz tās virsmas ir arī labi zināms:
![]()
Tad kopējais potenciāls uz ārējās sfēras virsmas ir:
![]()
Risinājums. Pirms sfēru savienošanas ar vadītāju, pirmās lādiņš bija vienāds ar:
Pēc savienojuma daļa lādiņa no iekšējās sfēras plūda uz ārējo. Strāva apstājās brīdī, kad bumbiņas potenciāls kļuva vienāds ar ārējā apvalka potenciālu. Tāpēc ērtāk ir meklēt nevis bumbas potenciālu, bet gan tai līdzvērtīgu ārējā apvalka potenciālu. Saskaņā ar iepriekšējā uzdevumā iegūtajiem rezultātiem šo potenciālu nosaka izteiksme:
![]()
kur q 1 un q 2 - attiecīgi lodītes un ārējā apvalka lādiņi pēc to savienošanas ar vadītāju. Saskaņā ar lādiņu nezūdamības likumu q = q 1 + q 2. Pēc vienkāršām pārvērtībām mēs iegūstam:
![]()
Sāksim ar attēlu, lai atrisinātu problēmu:
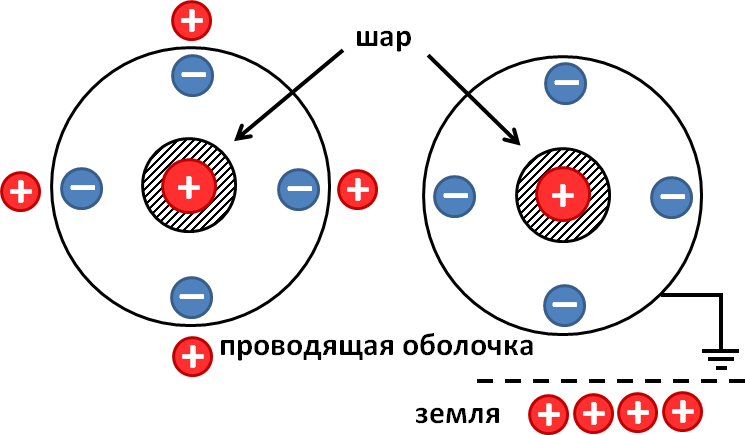
Pēc vadošā apvalka zemēšanas viss pozitīvais lādiņš, kas uz tā veidojas elektrostatiskās indukcijas fenomena dēļ, plūst uz zemi. Uz tā paliek tikai negatīvais lādiņš, jo to pievelk iekšējās sfēras pozitīvais lādiņš
Risinājums. Zinot bumbiņas potenciālu sākotnējā laika momentā un tās rādiusu, mēs varam atrast uz tās lādiņu:
Sakarā ar ārējā apvalka elektrostatiskās indukcijas parādību, jānotiek lādiņa atdalīšanai. Negatīvais lādiņš plūdīs uz korpusa iekšējo virsmu, pozitīvais lādiņš uz ārējo (skat. attēlu). Tāda pati parādība radās arī iepriekšējās problēmās, bet mēs to neņēmām vērā. Kāpēc? Problēmu apstākļos tika norādīts, ka apvalks ir plāns, un šāda lādiņu "aizbēgšana" nav izraisījusi būtiskas izmaiņas elektrostatiskā lauka konfigurācijā.
Šajā uzdevumā grāmatvedība šī parādība svarīgi, jo apvalks ir iezemēts. Pēc zemējuma pozitīvais lādiņš no čaulas notecēs zemē, paliks tikai negatīvais. q 2, jo to piesaista pozitīvs lādiņš q 1 iekšējā sfēra. Iezemētā apvalka potenciāls kļūs vienāds ar zemes potenciālu, tas ir, nulle. Šajā sakarā un saskaņā ar rezultātu, kas iegūts, risinot pirmo uzdevumu, mēs iegūstam vienādību:
Izmantojot pirmajā uzdevumā iegūto šādas sistēmas iekšējās sfēras potenciāla aprēķina izteiksmi, beidzot atrodam nepieciešamo lodītes potenciālu:
![]()
![]()
Pieredze rāda, ka reti kurš ar pirmo reizi saprot šo problēmu risinājumu visās detaļās. Parasti ir nepieciešams ilgi un neatlaidīgi izskaidrot skolēniem visus tos sīkumus, kuru atrisinājums tiek reducēts uz tukšām burtisku izteicienu pārveidojumiem, lai iegūtu mācību grāmatas beigās sniegto atbildi. Nav viegli izprast šo uzdevumu fizisko būtību un iemācīties iegūtās zināšanas pielietot nākotnē. Taču šī ir šīs tēmas galvenā metodiskā vērtība skolas fizikas kursā. Labākais palīgs savā pētījumā noteikti būs profesionāls pasniedzējs, kompetents mentors, kurš var izdomāt jums saprotamu skaidrojumu un atbildēt uz visiem jūsu jautājumiem. Starp citu, ja tādi ir, varat tos jautāt zemāk komentāros.
Sergejs Valerijevičs