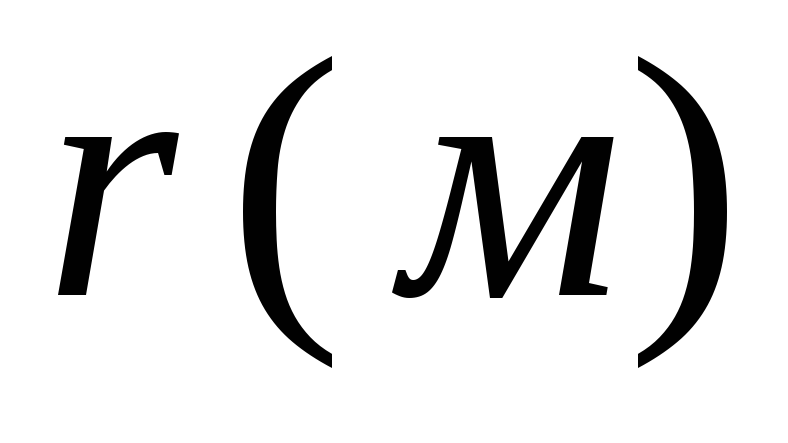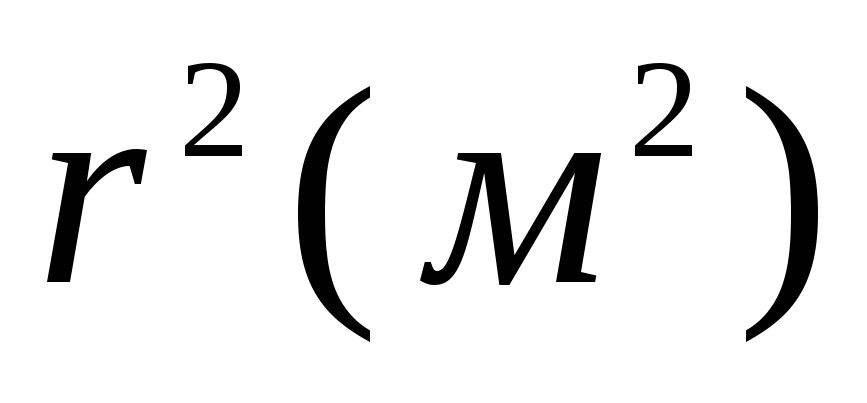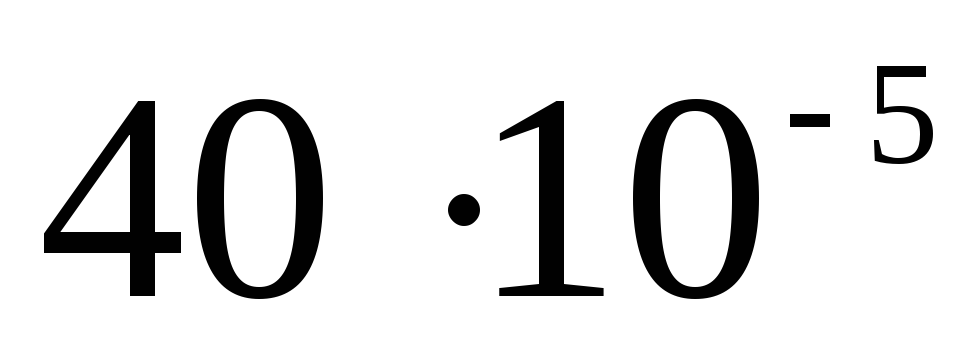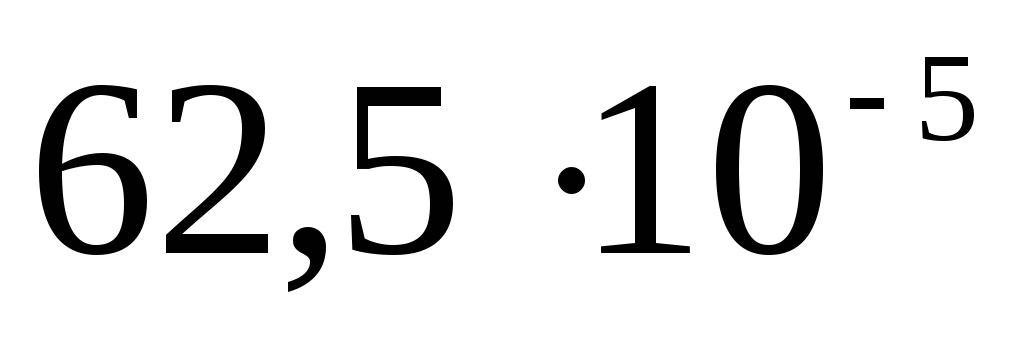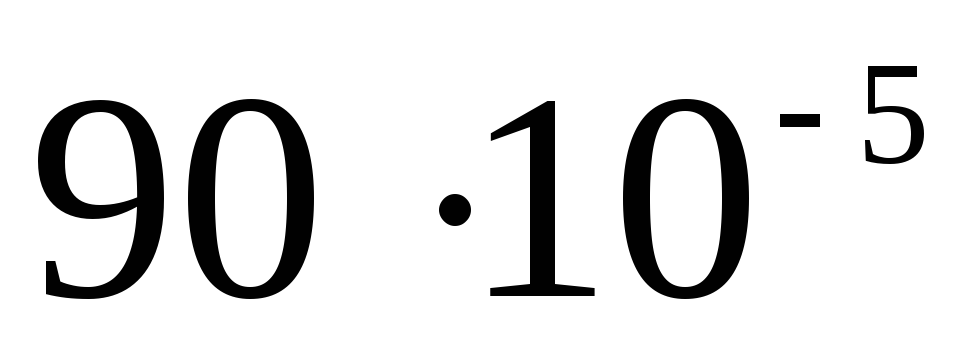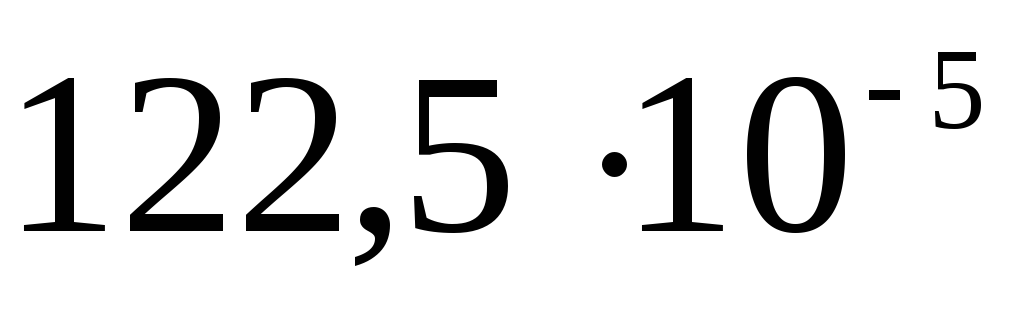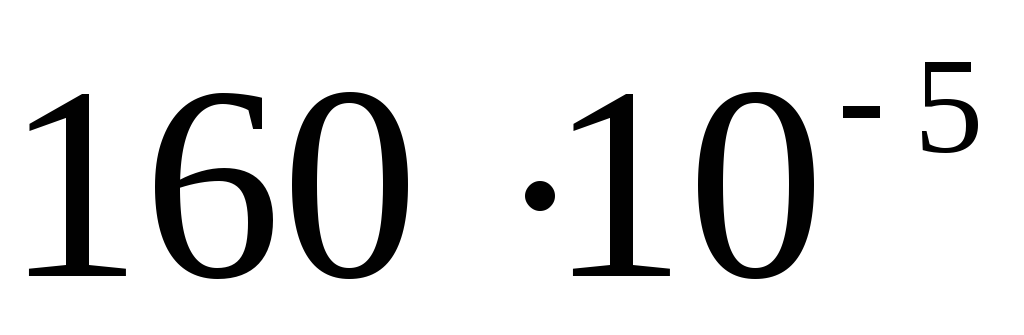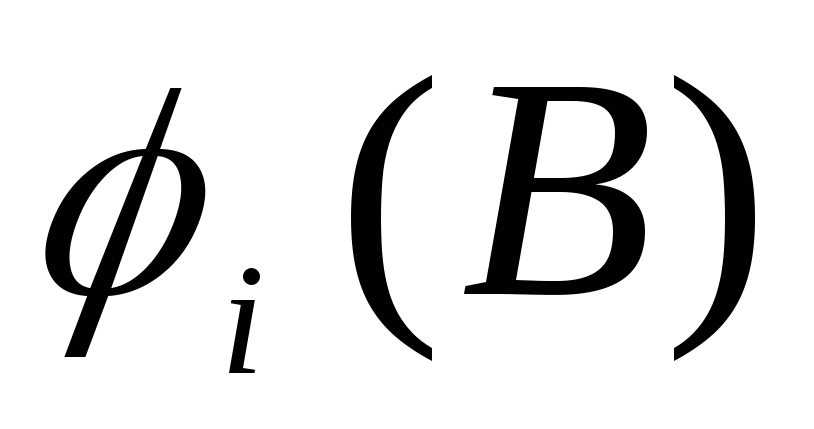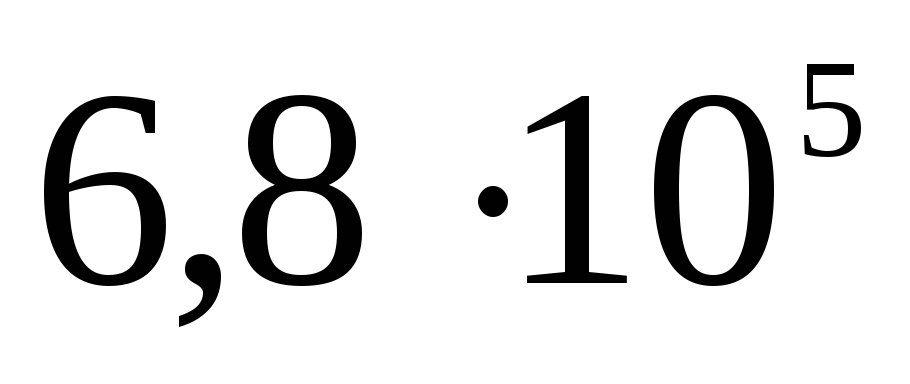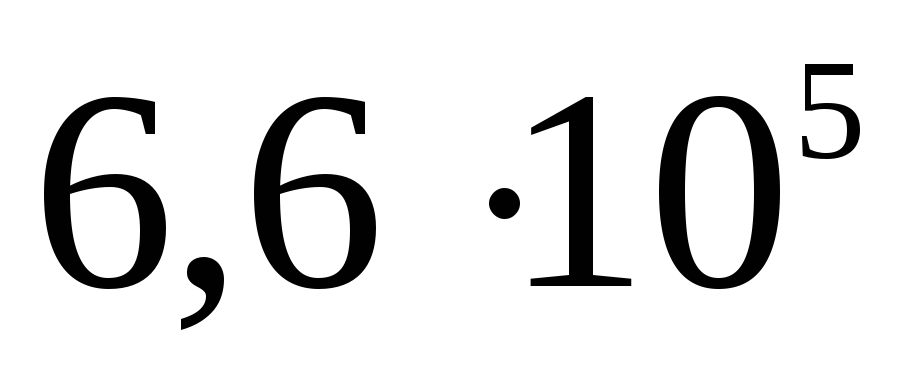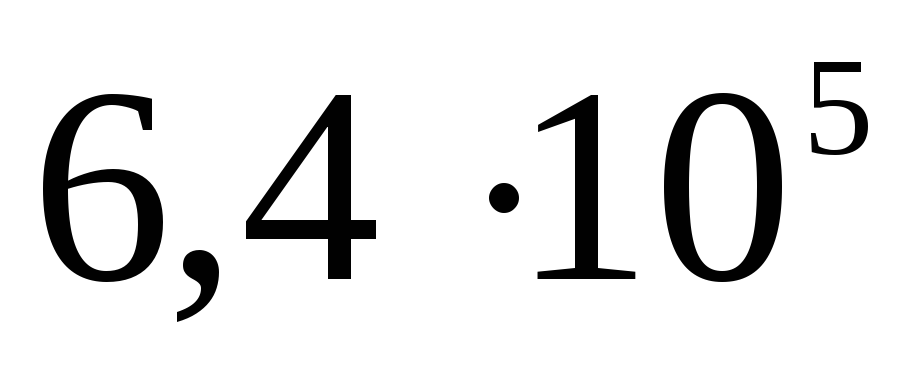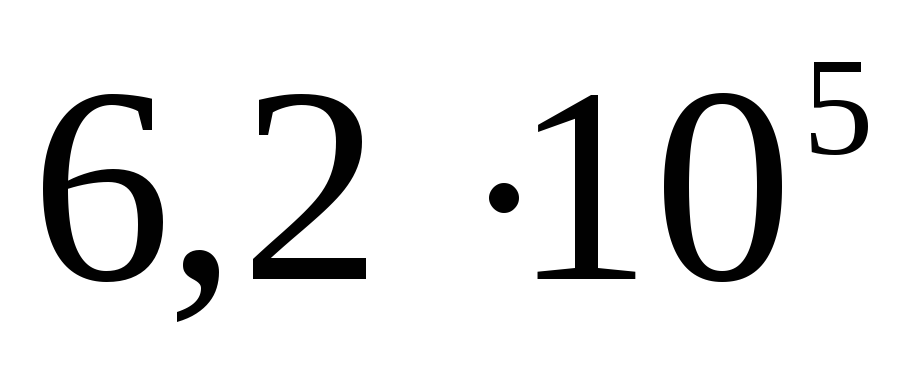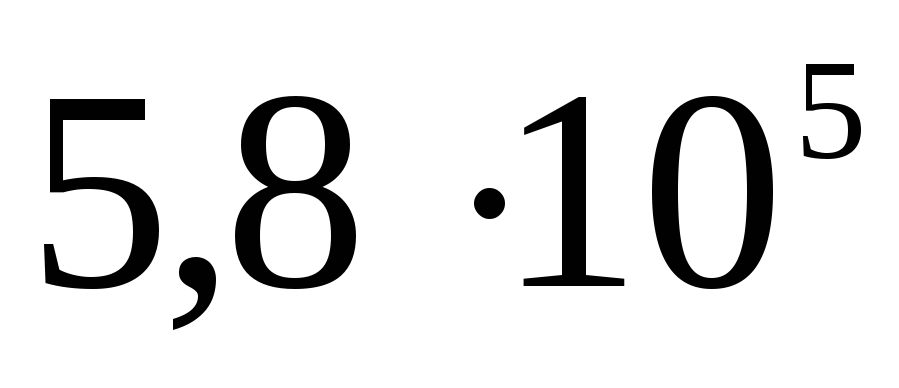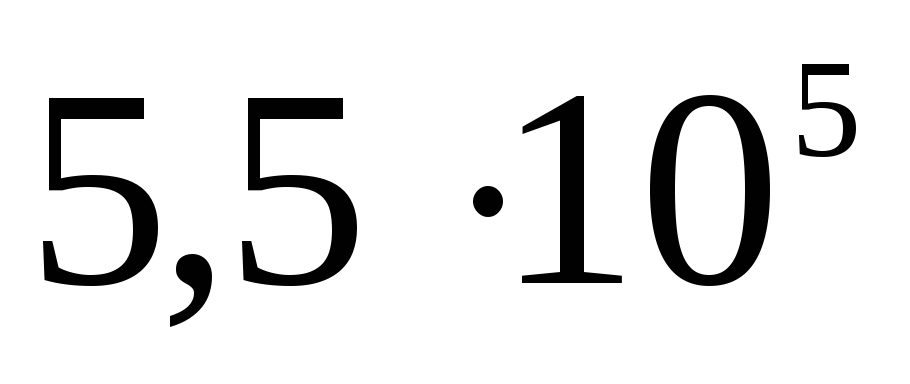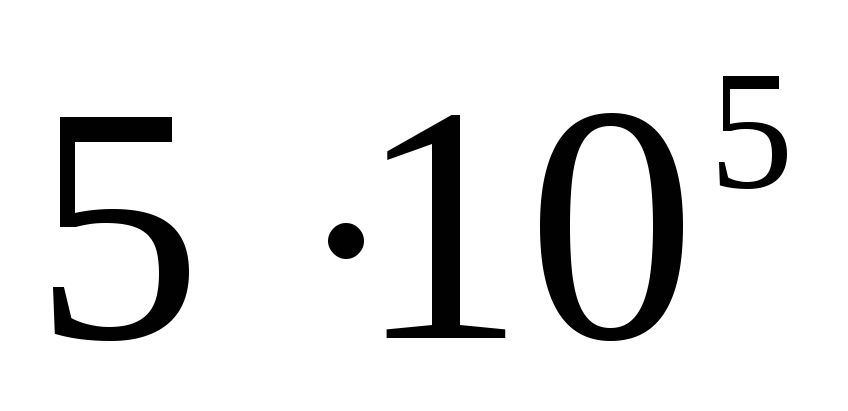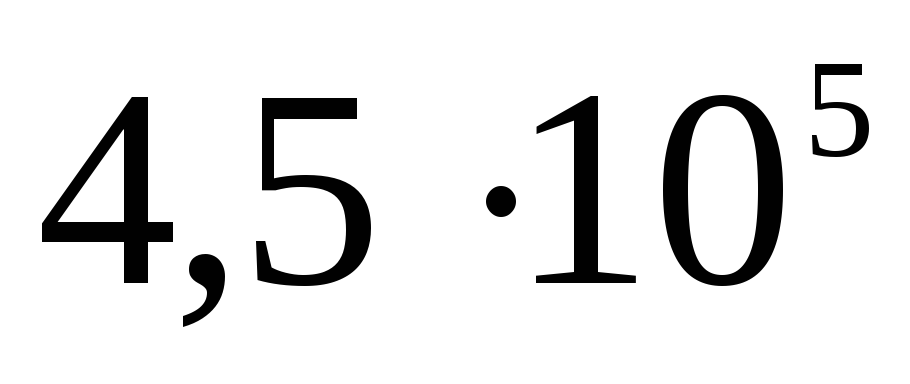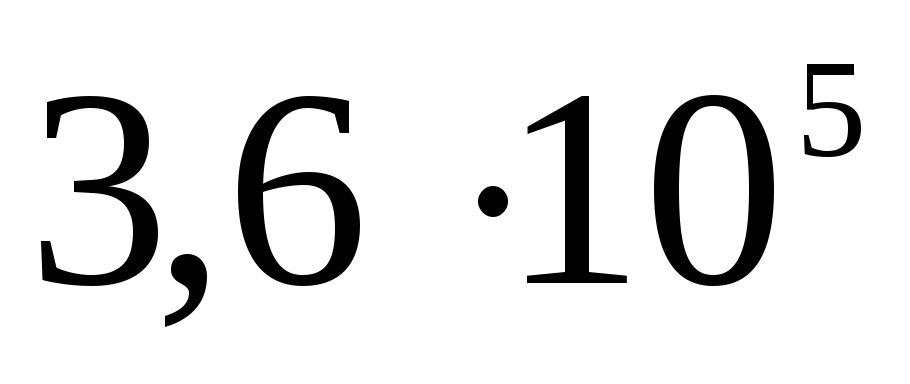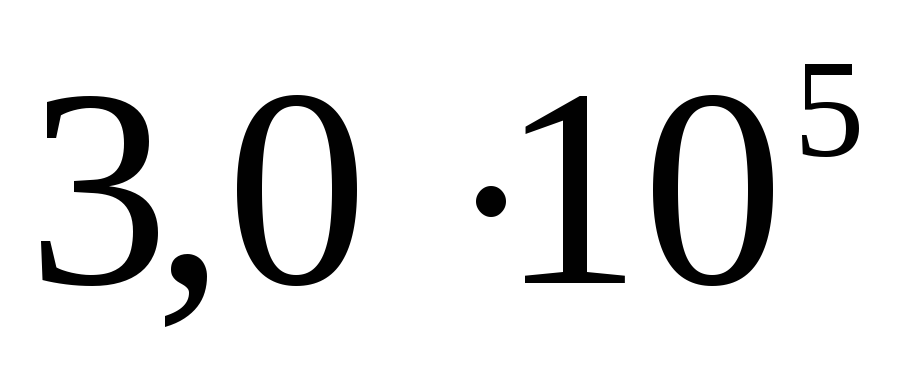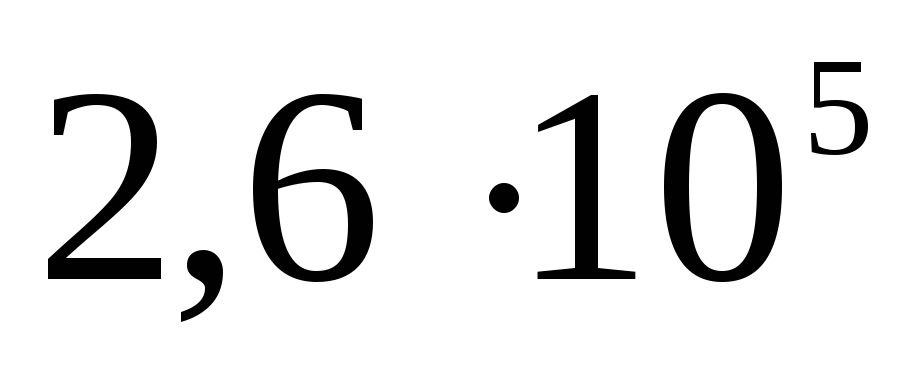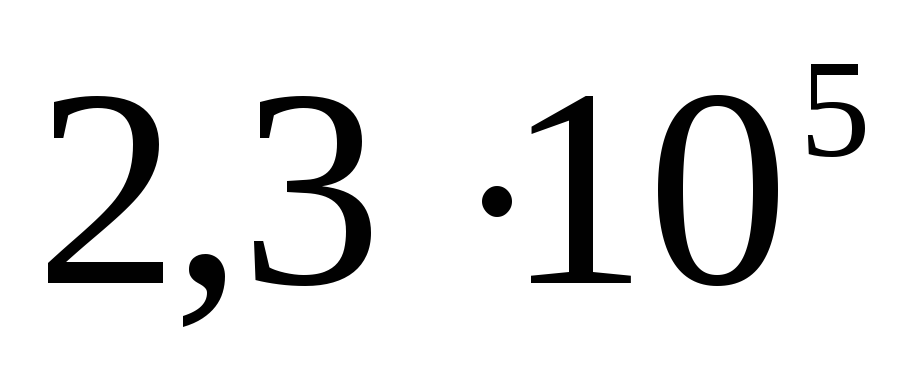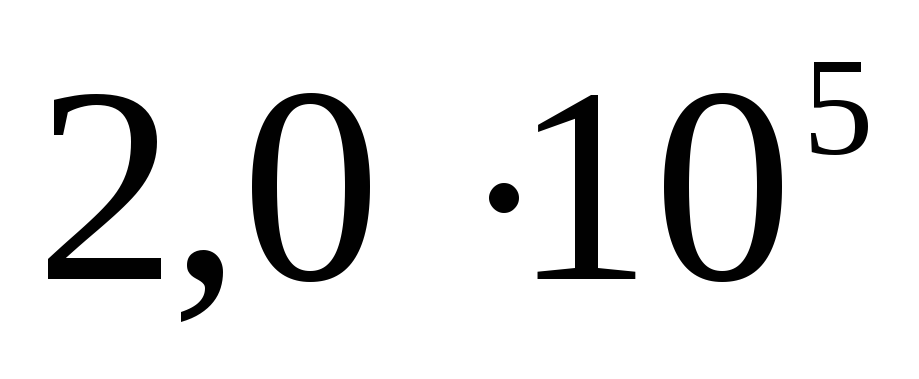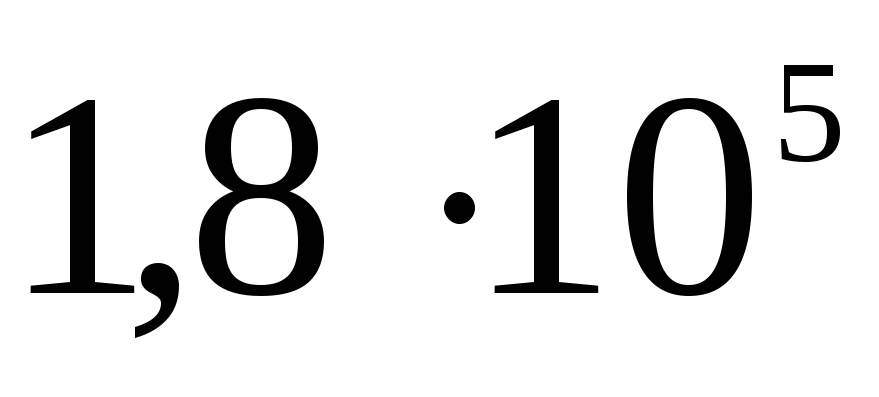Elektrostatika
1
(CT 2001 9 testas. A19). Laidus rutulio spindulys R
turi teigiamą krūvį +
q
. Jei 2 atstumu R nuo rutulio centro pastatykite taškinį neigiamą krūvį -2 q, tada potencialas kamuolio centre
Dažna klaida sprendžiant, tai kyla iš neteisingos formuluotės aiškinimo: „laidaus rutulio viduje nėra lauko“. Iš šio teiginio daroma klaidinga išvada: abi lauko charakteristikos: ir intensyvumas, ir potencialas yra lygūs nuliui. Tiesą sakant, šiuo atveju tik lauko stiprumas yra lygus nuliui, nes laisvieji krūviai nustoja judėti laidininko paviršiumi, kai vektorius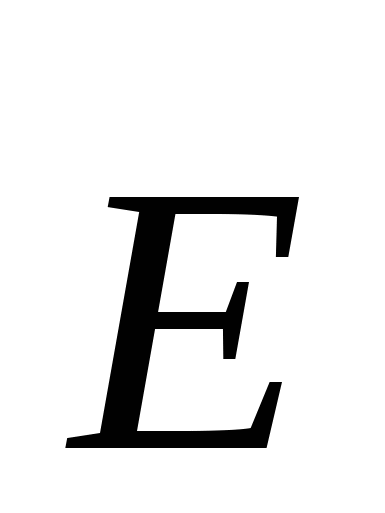 
bet kuriame paviršiaus taške yra jam statmenas. Laidininko paviršius šiuo atveju yra ekvipotencialus. Bandomojo krūvio judėjimo tūryje, kurį riboja paviršius, darbas yra lygus nuliui, nes jėga, veikianti krūvį, lygi nuliui; iš to išplaukia, kad judant iš taško į tašką potenciali krūvio energija nekinta: elektrinis potencialas tūryje, kurį riboja laidus paviršius, yra pastovus ir lygus potencialui pačiame paviršiuje. Įkrautos sferos intensyvumo ir potencialo kitimas, esant atstumui nuo krūvio centro, gali būti pavaizduotas grafikais (žr. pav.).
Sprendimas
Sferiškai simetriškai paskirstyto krūvio sukuriamas potencialas q rutulio centre, toks pat kaip ir jo paviršiuje ir lygus φ 1 = q/4 πε 0 R; potencialas, sukurtas tame pačiame taške taškinio krūvio -2 q esantis už sferos ribų 2 atstumu R nuo jo centro yra φ 2 = – 2 q/4 πε 0 2 R; potencialas rutulio centre yra dviejų laukų superpozicijos rezultatas, t.y. φ = φ 1 + φ 2 = q/4 πε 0 R–2 q/4 πε 0 2 R= 0 .
Darant bandomieji elementai patogu, kad įėjimas būtų kuo trumpesnis. Pavyzdžiui, šiuo atveju pakanka vienos bendrosios lygties φ = q/4 πε 0 r.
Nes taškinis neigiamas krūvis yra dvigubai didesnis už sferoje paskirstytą krūvį ir yra dvigubai toliau nuo sferos centro, iš parašytos lygties matyti, kad abiejų krūvių potencialai yra vienodo dydžio ir priešingi ženklu, todėl gaunamas potencialas yra 0.
2 (CT 2001 testas 11. A 19).
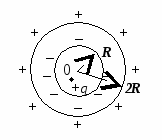Viduje sferinis metalo sluoksnis, kurio vidinis ir išorinis spinduliai yra atitinkamai lygūs R
ir 2
R
,
ant atstumo R/
2
q
.
Potencialas sferos centre yra...
Sprendimas
Sunkumai sukelia krūvių pasiskirstymo sferinio sluoksnio paviršiuose paveikslo konstravimą.
Dėl elektrostatinės indukcijos vidiniame rutulio paviršiuje atsiranda krūvis –
q
, o išorėje + q
.
Potencialas sferos centre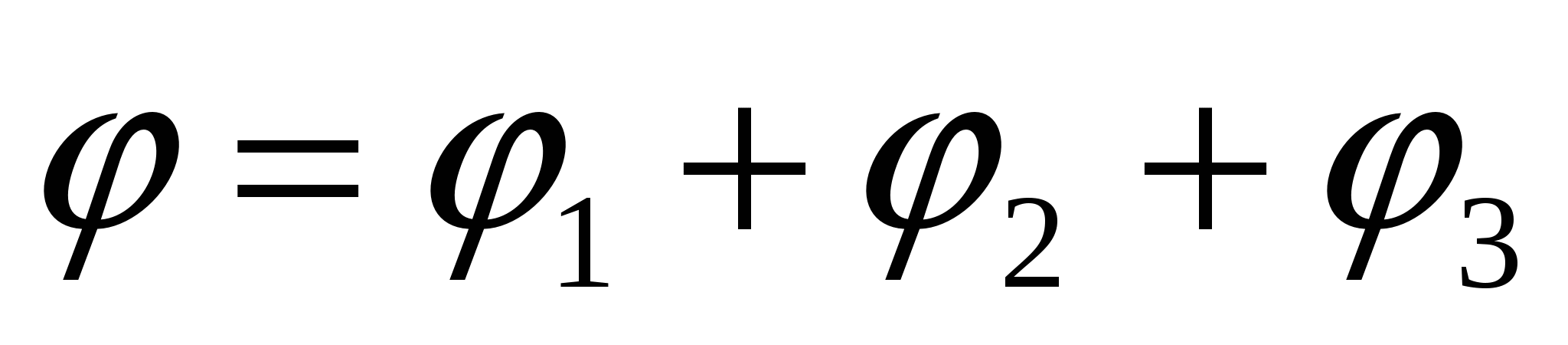 
;
; 
; 
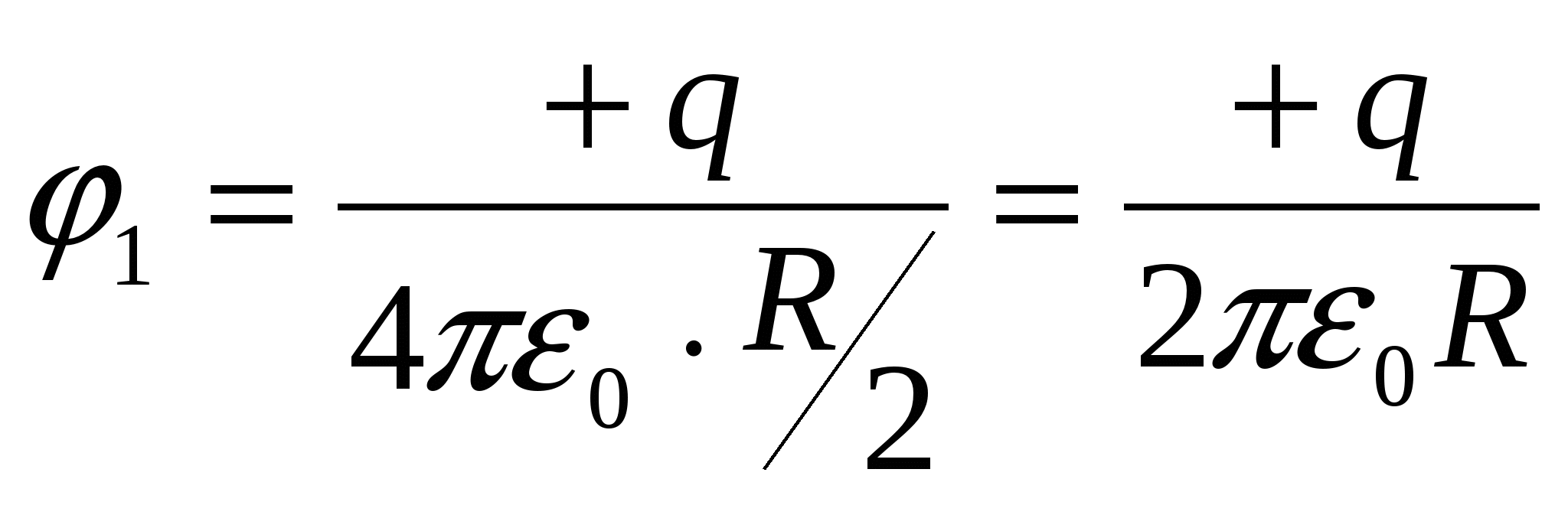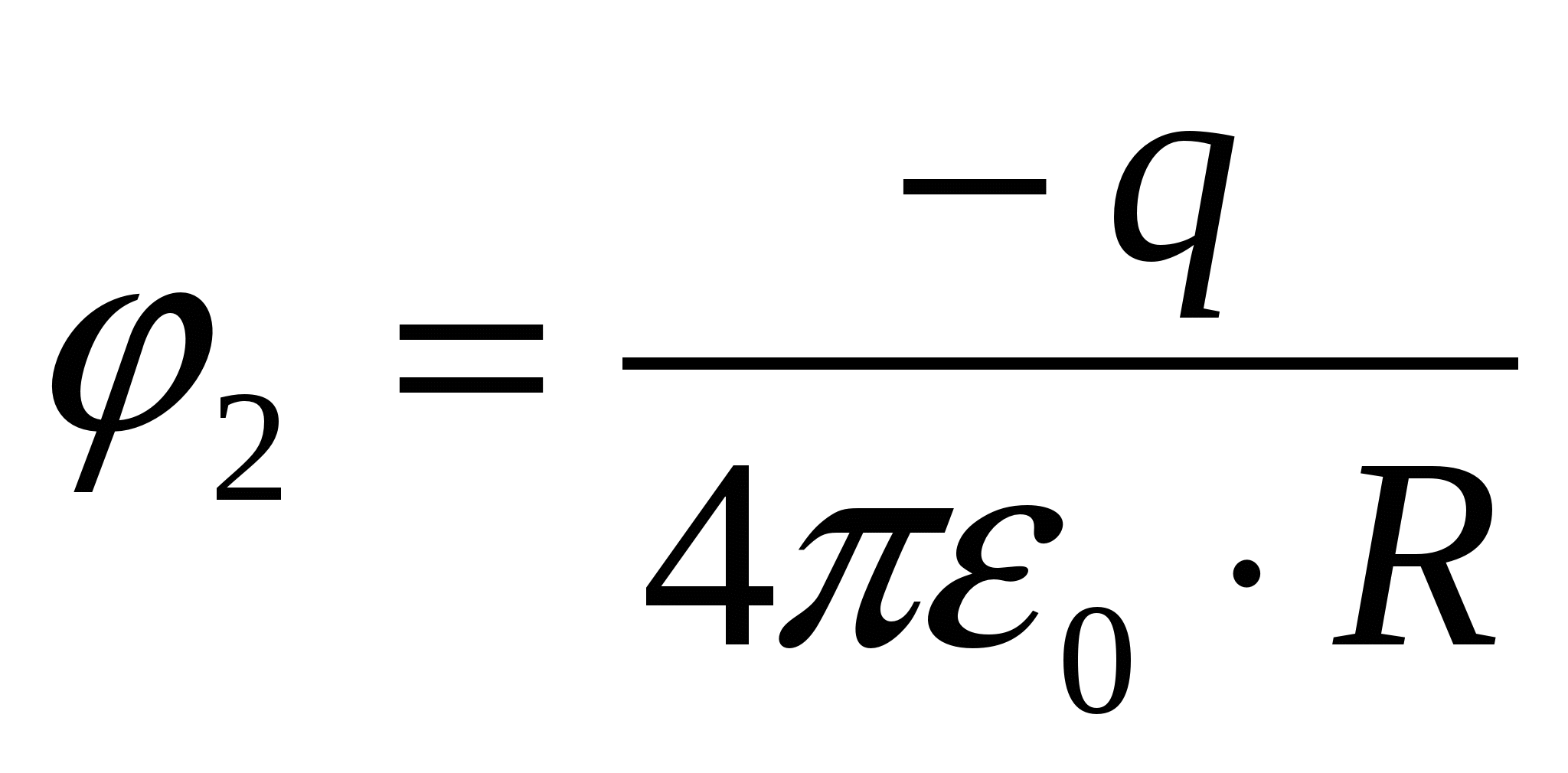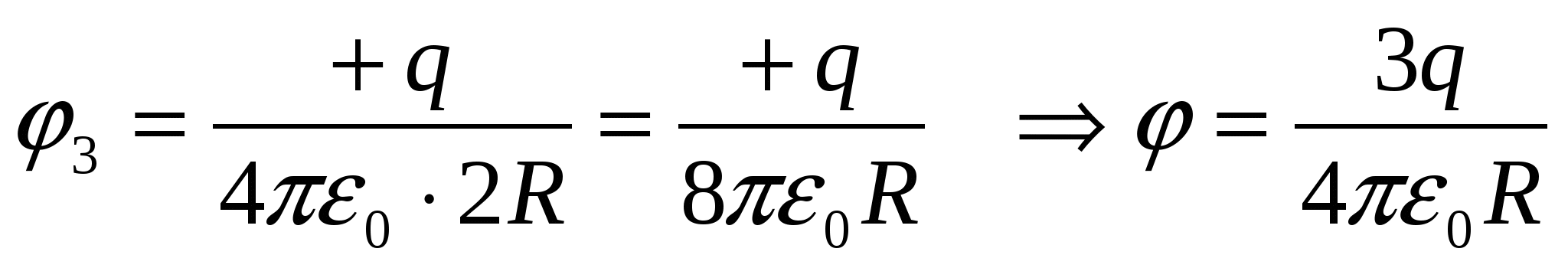– atsakymas 1.
Panaši užduotis – A 19 teste Nr.12, 2001 m. :
Sferinio metalo sluoksnio viduje, kurio vidinis ir išorinis spindulys yra atitinkamai lygus 2 R ir 4 R , ant atstumo R iš centro yra taškinis teigiamas krūvis q . Potencialas sferos centre yra….
Atsakymas: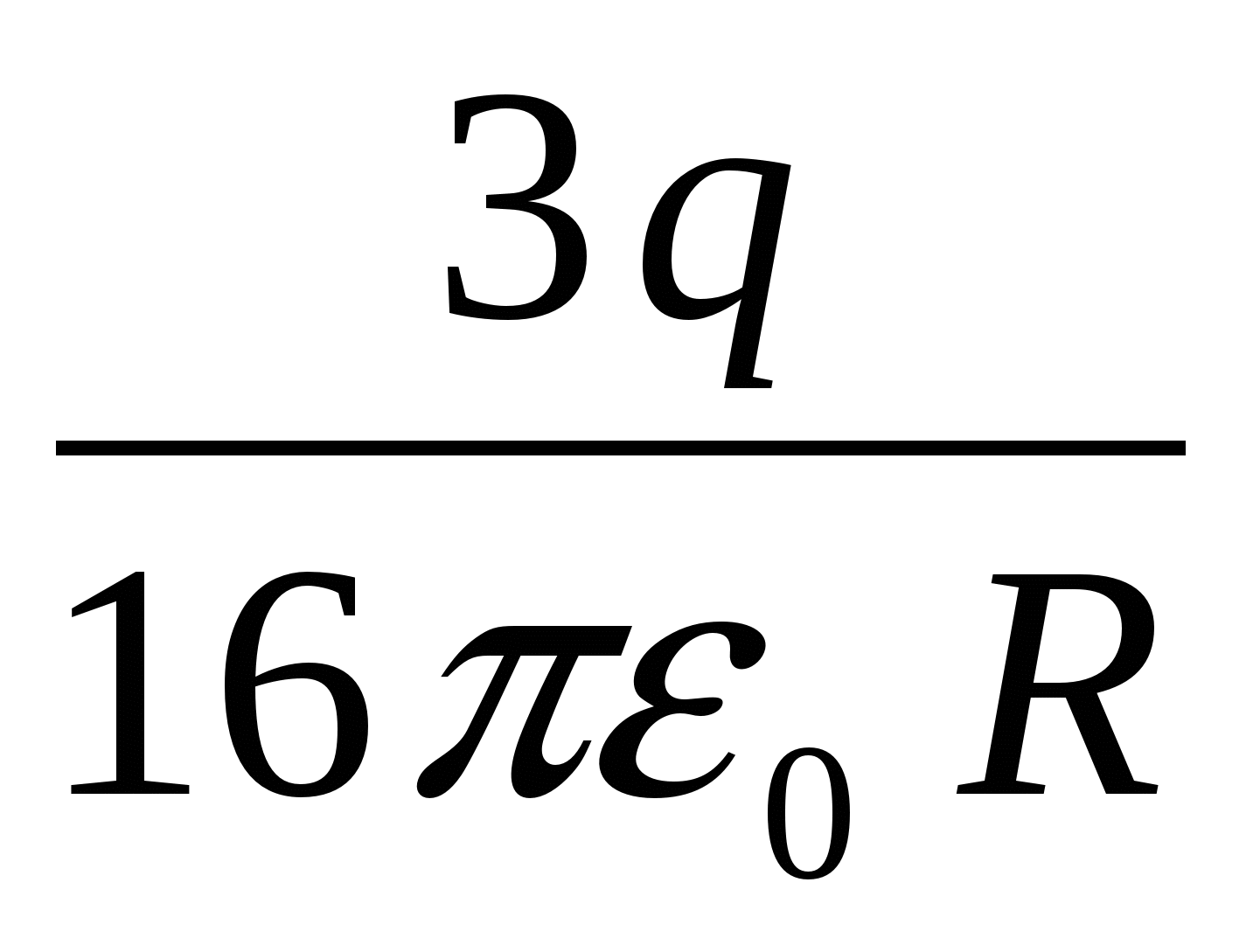 
3 (CT 2000 testas ... A19). Metalinis rutulys su spinduliu R 1 turintis potencialo φ 1 , apsuptas neįkrautu sferiniu laidžiu apvalkalu, kurio spindulys R 2 . Rasti rutulio potencialą, kai jis kurį laiką buvo prijungtas prie apvalkalo?
Sprendimas
Įkrauto kamuolio potencialas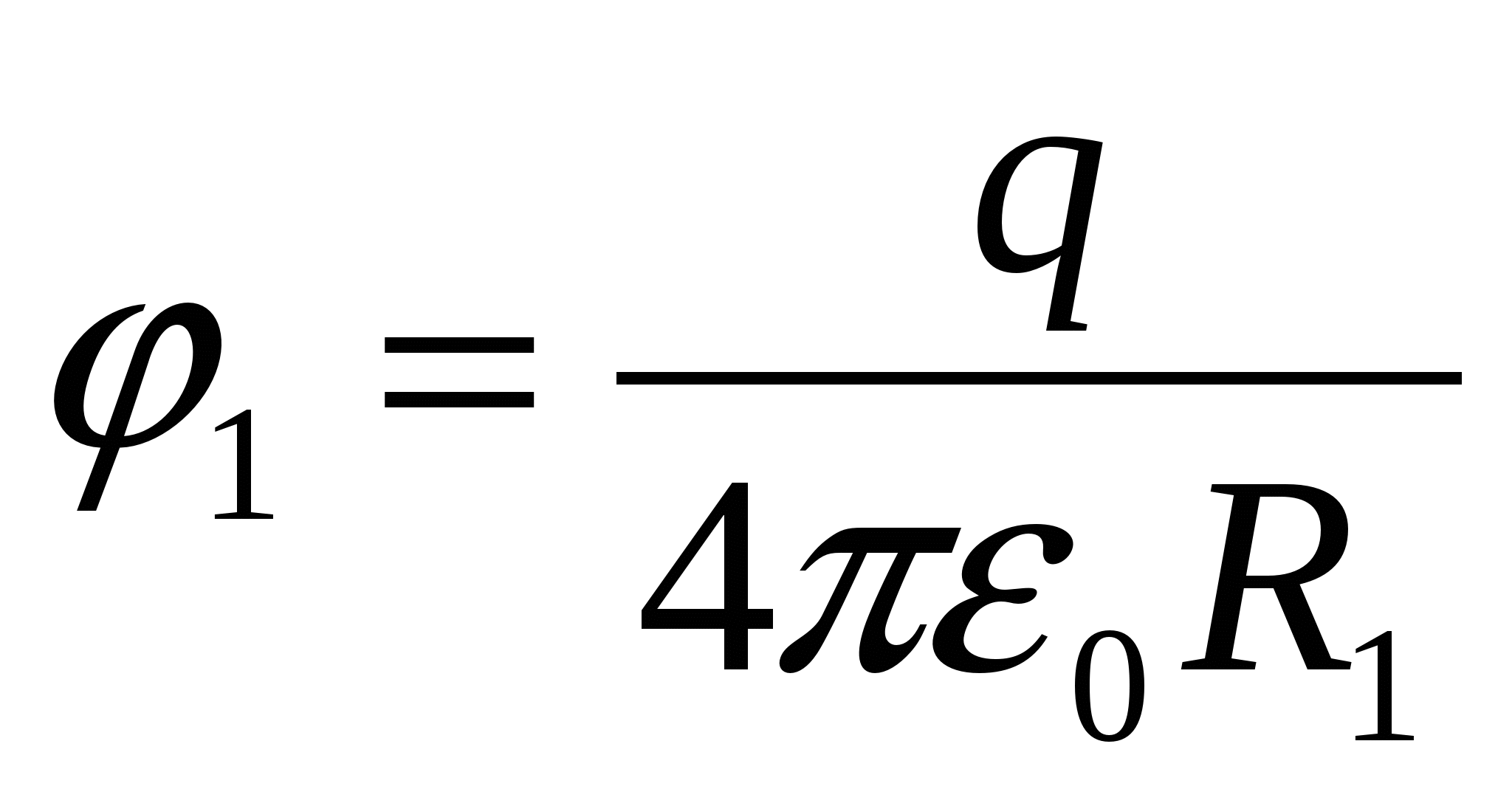 
.
Jei įkrautas rutulys paliečia vidinį apvalkalo paviršių, krūviai bando nusistovėti ant galimo dideli atstumai vienas nuo kito, eikite į apvalkalą. Lauko stiprumas apvalkalo viduje tampa lygus 0, lauko potencialas apvalkalo taškuose ir jo viduje lygus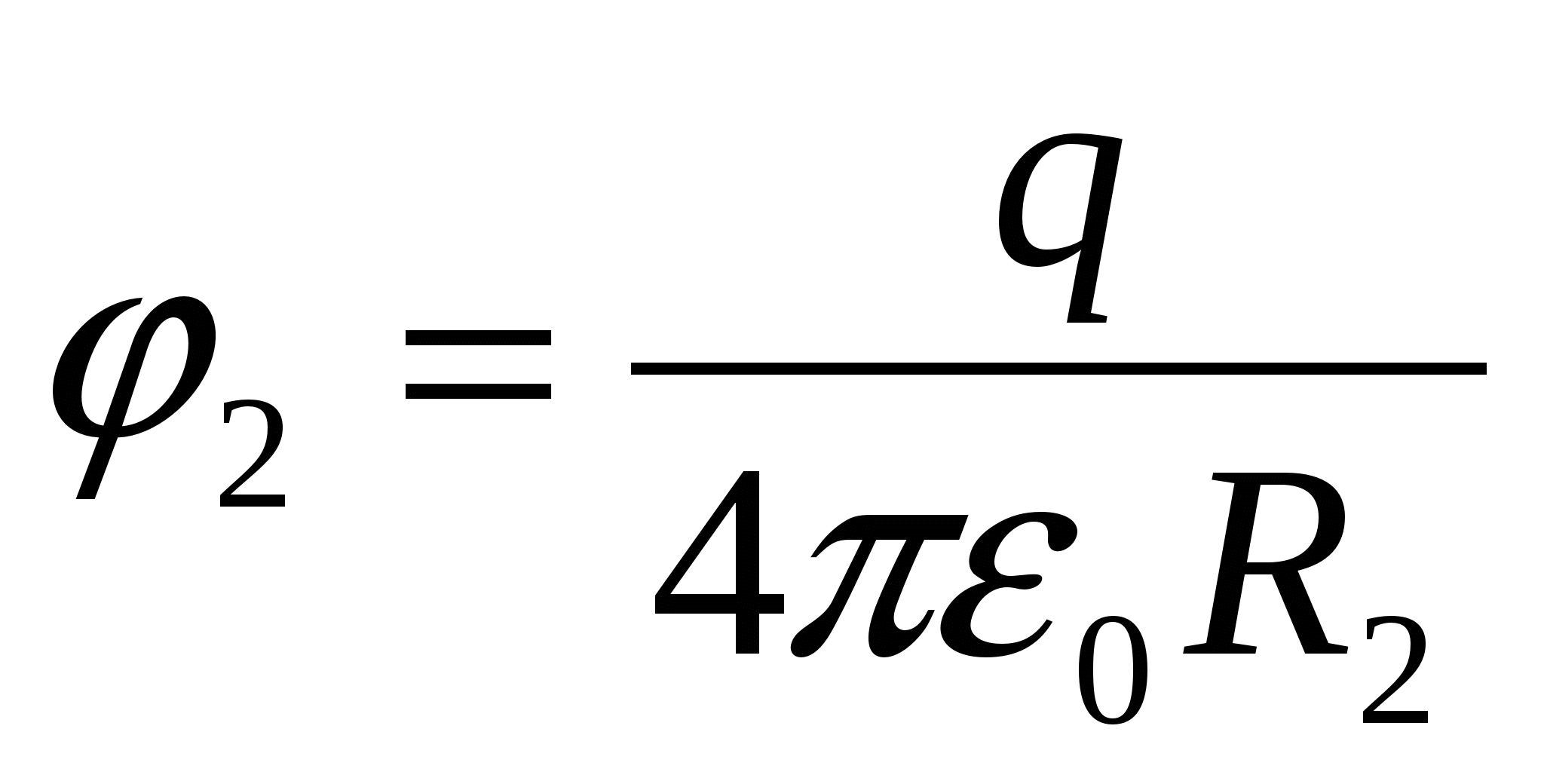 
(bet ne 0!Žr. ankstesnę problemą), kur 
. Taigi korpuso ir jo viduje esančio ir su juo sujungto rutulio potencialas lygus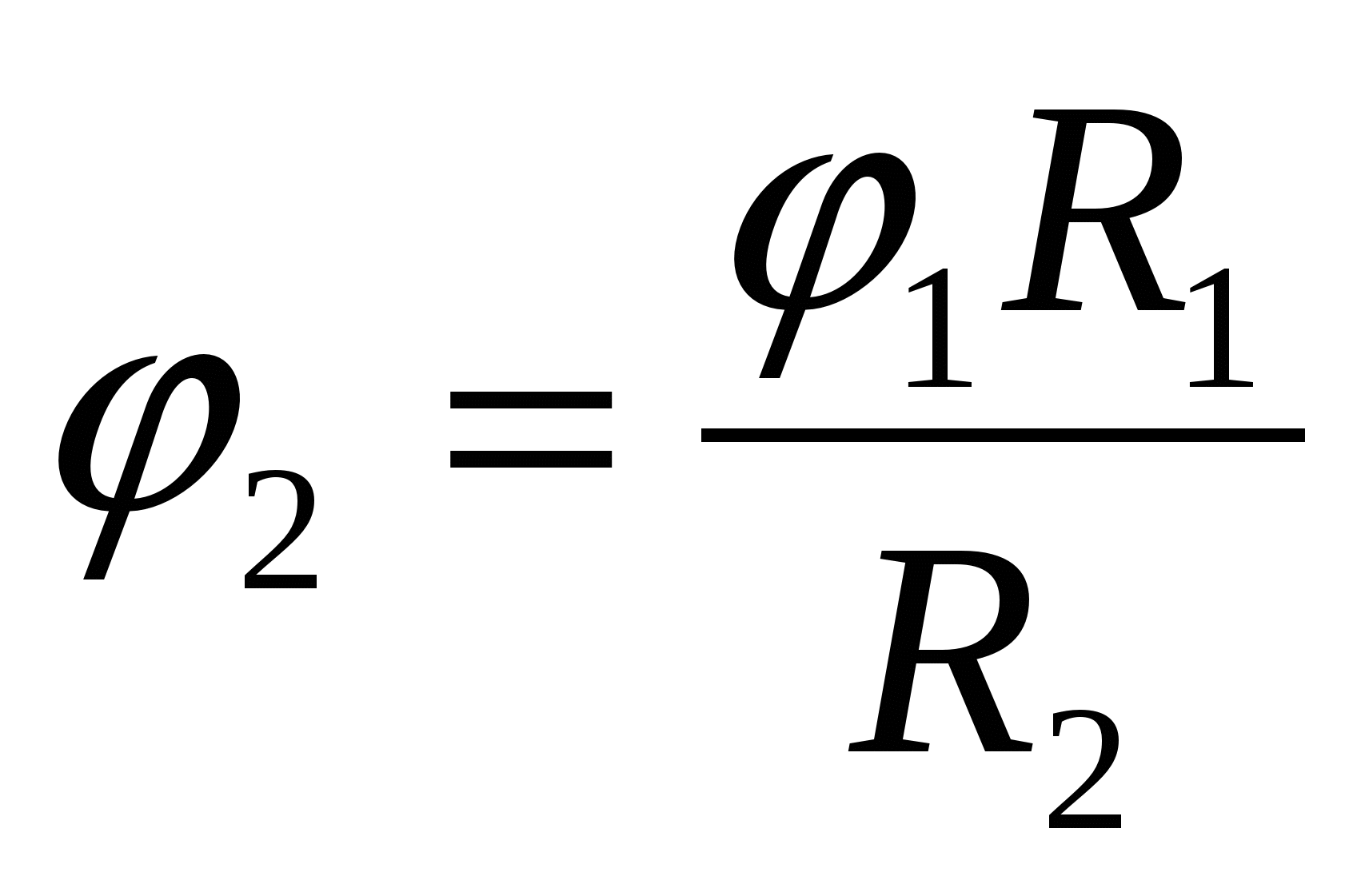 
– atsakyti.
Teisingai atsakymas -1.
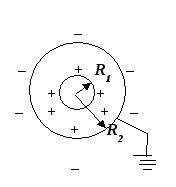
4 (CT 2000 testas ... A19). Metalinio rutulio spindulys R 1 turintis potencialo φ 1 , apsuptas sferinio spindulio laidaus apvalkalo R 2 . Koks bus rutulio potencialas, jei apvalkalas bus įžemintas?
Sprendimas
Dažniausias klaida yra tai, kad neatsižvelgiama į lauko potencialą, kurį sukuria krūviai, kuriuos sukelia apvalkalas, kai jis įžemintas.
Pirmas variantas sprendimus. Rutulio paviršiaus potencialas, sukurtas kamuoliuko krūvio metu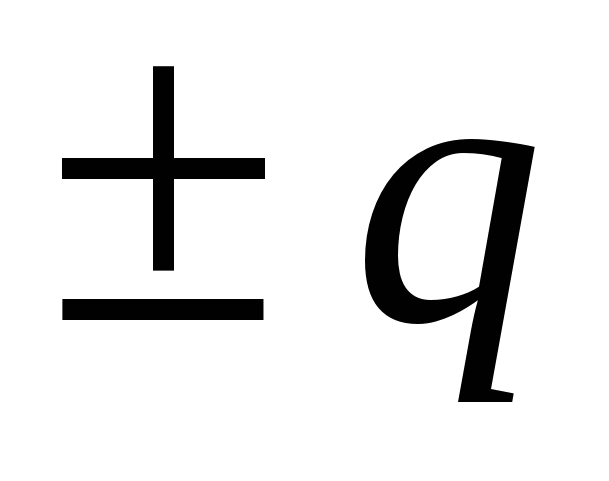 
, yra lygus 
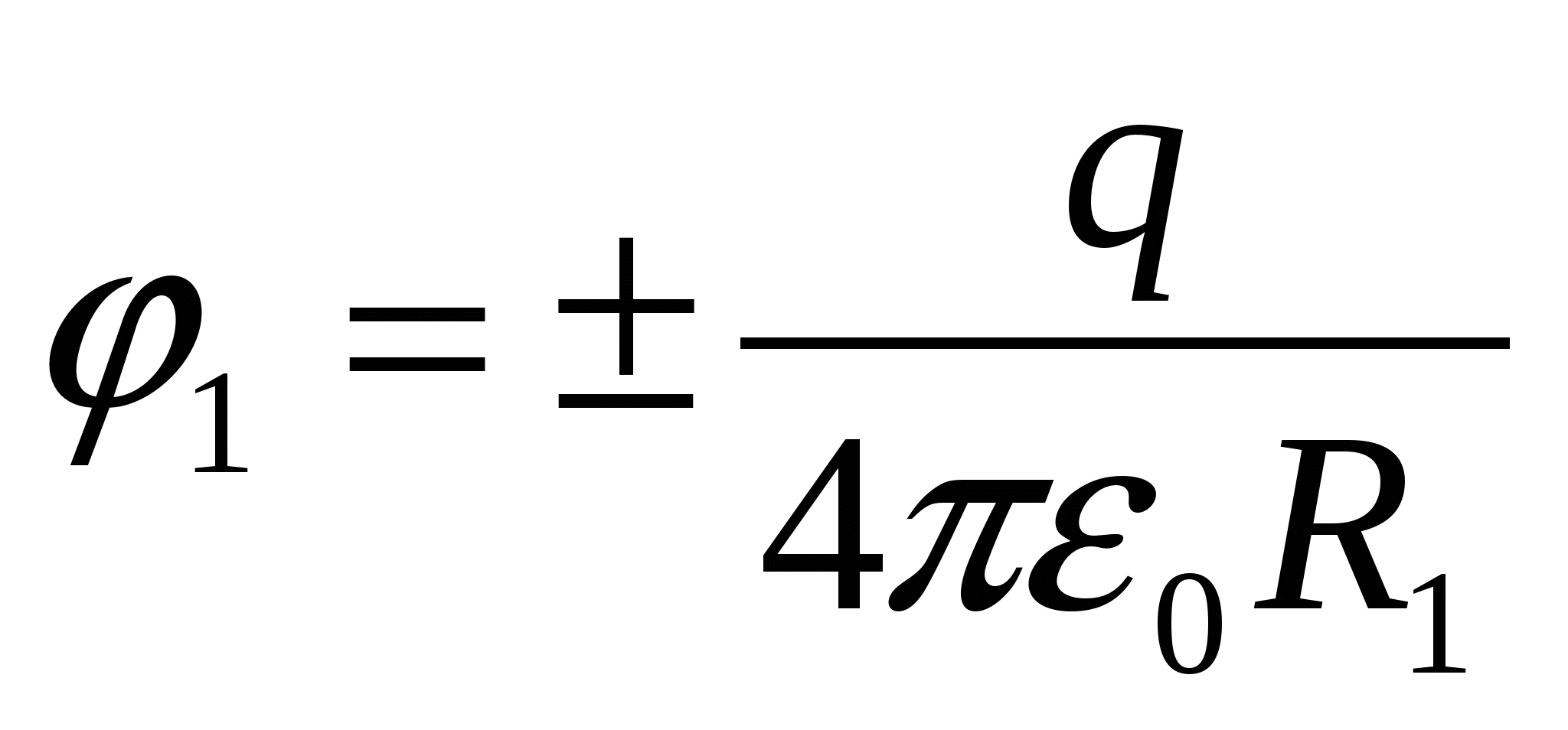. Įžeminus apvalkalą, ant jo atsiranda sukeltas krūvis 
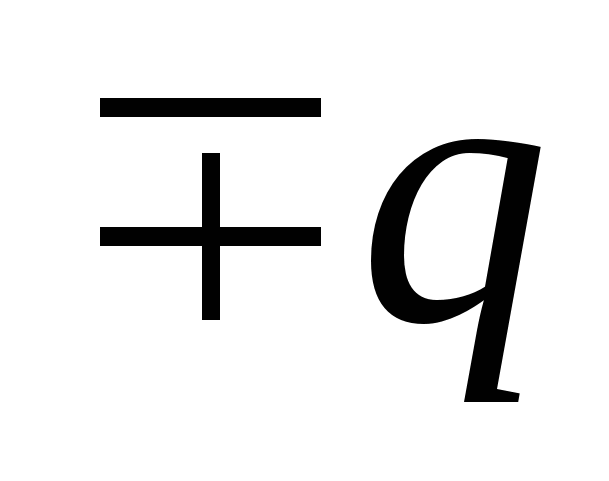, kuris ant apvalkalo ir jo viduje sukuria potencialą 
.
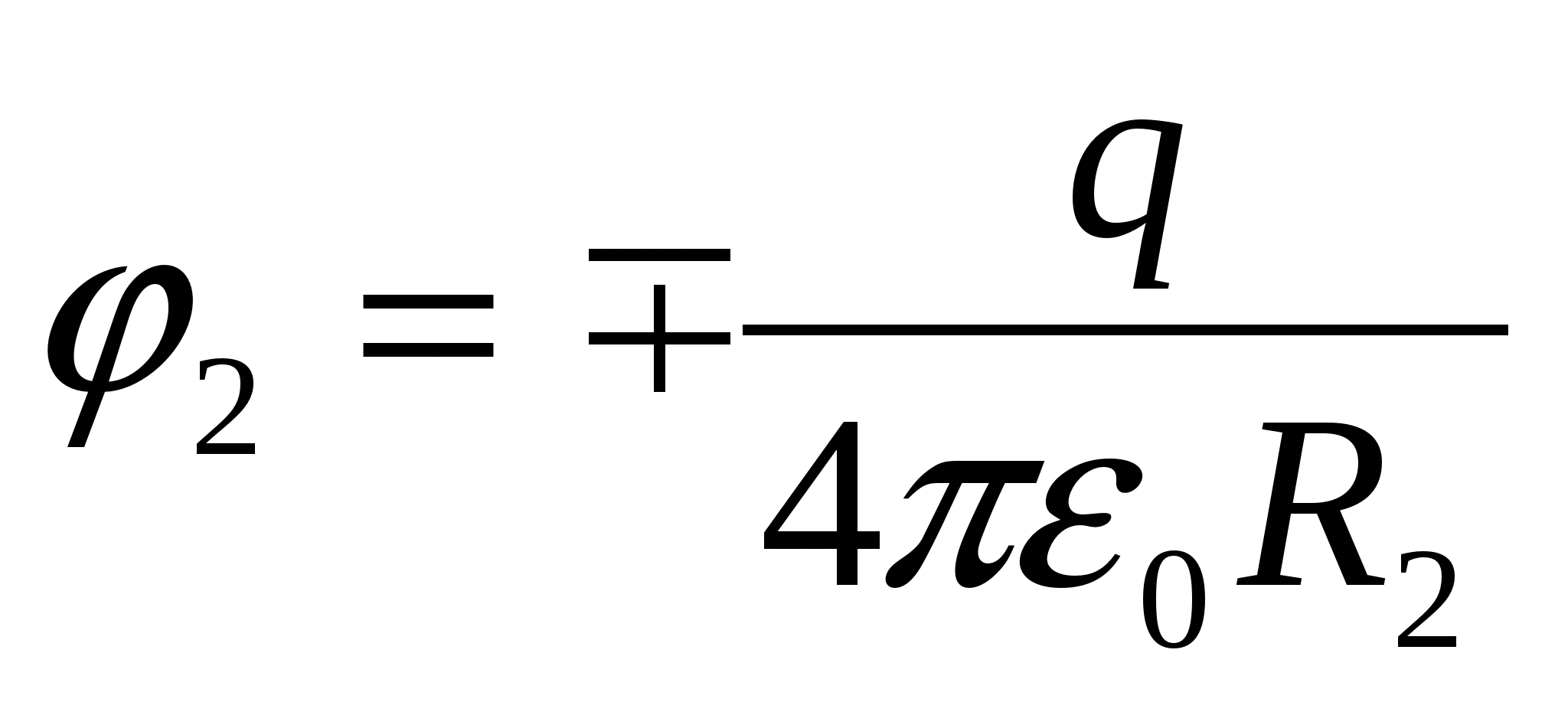Pradinio rutulio lauko ir lauko, kurį sukuria sukeltas apvalkalo krūvis, superpozicija suteikia potencialą rutulio paviršiuje
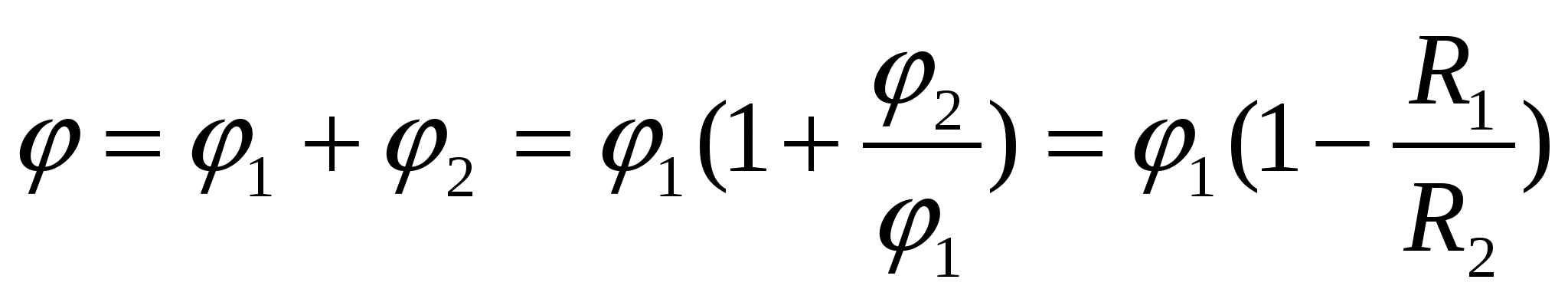– atsakyti.
Antras variantas sprendimus. Galima ginčytis, kad apvalkalo potencialas po įžeminimo yra 0, kaip įprasta technikoje (potencinės energijos atskaitos tašku imamas įžemintas apvalkalas), iš šios sąlygos randamas indukuoto krūvio dydis ir ženklas. Korpuso potencialas φ 2 yra potencialo, atsirandančio dėl jo sukelto krūvio, suma q 2 ir kamuolio lauko potencialą φ 1 :
, 
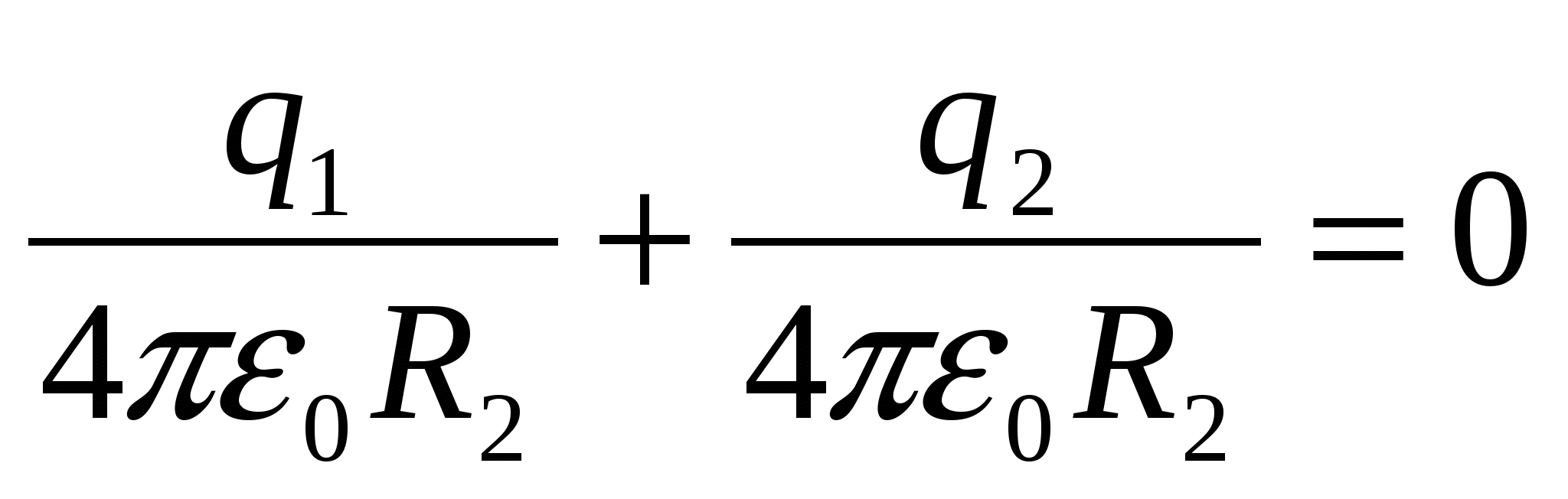q 1
= –
q 2.
.
Surandame rutulio potencialą po to, kai apvalkalas yra įžemintas:
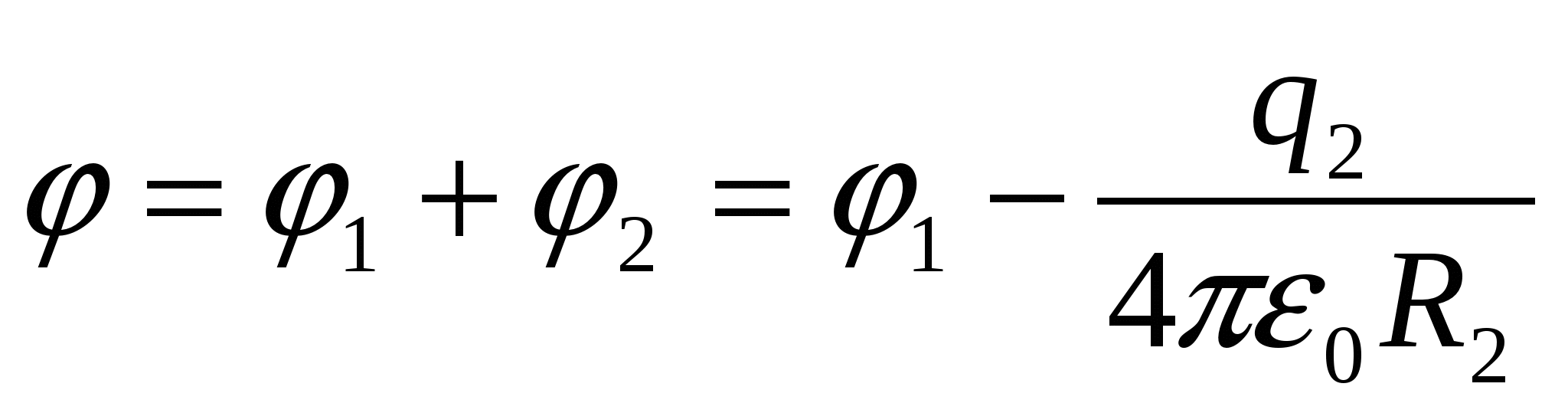(1).
Iš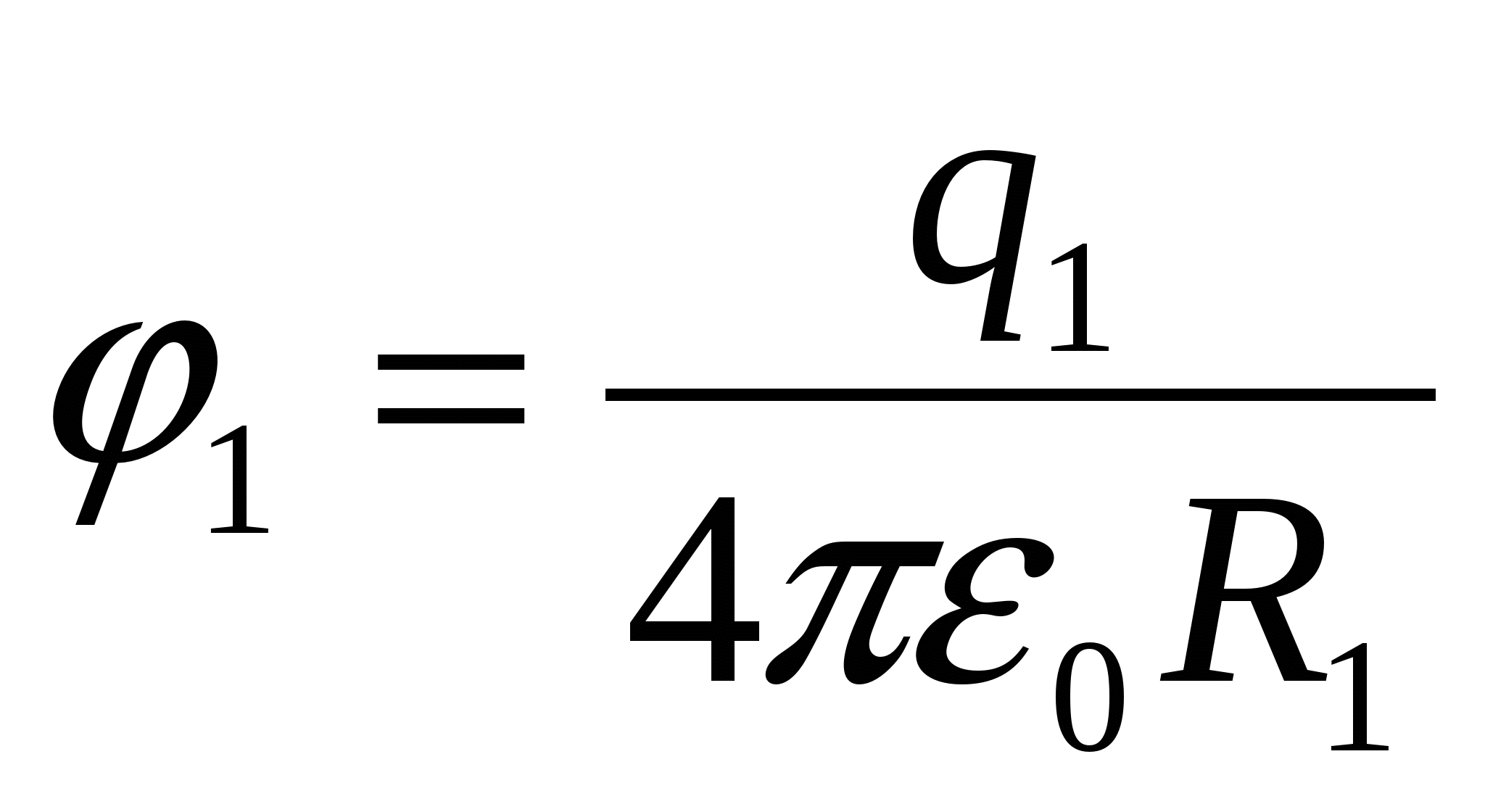 
rasti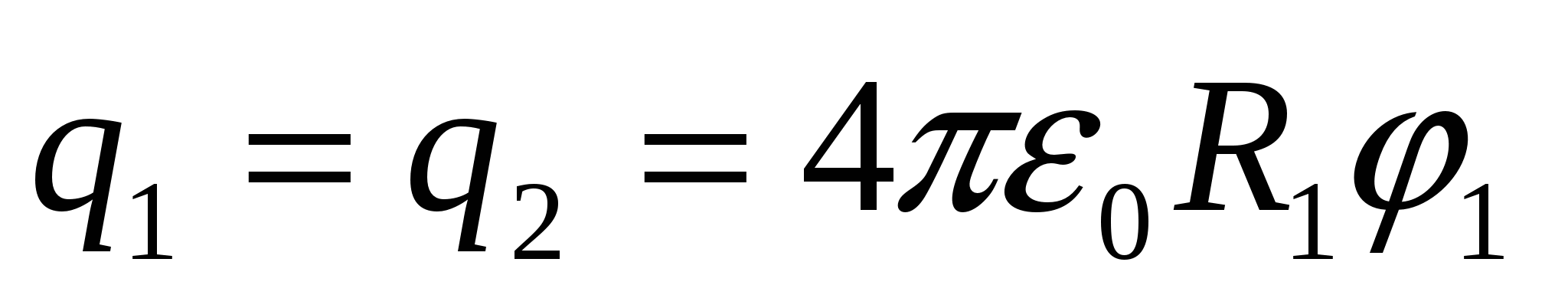 
, pakeičiame į (1), gauname atsakyti: 
.
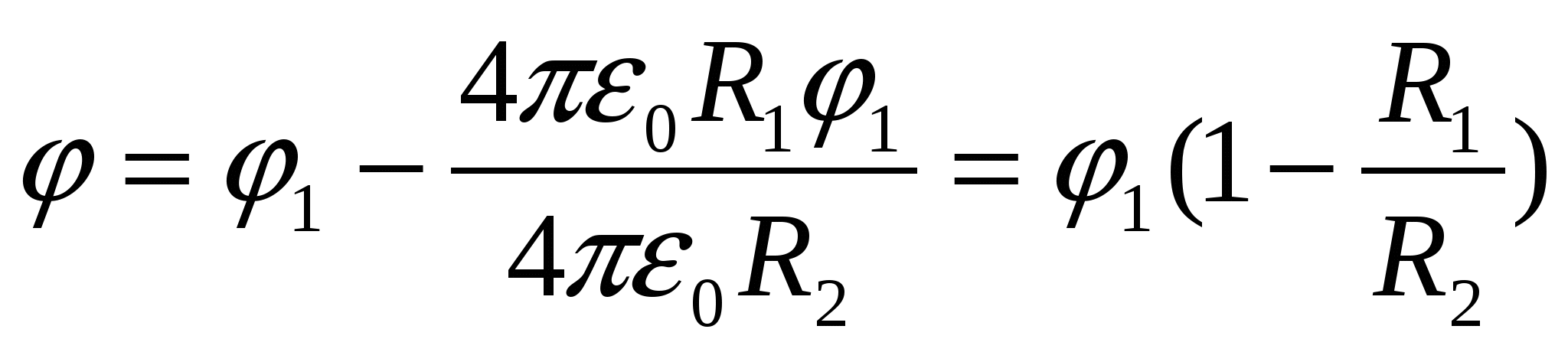Šis sprendimas turi tam tikrų trūkumų:
– anksčiau spręstuose uždaviniuose potencialas (potencinė energija) buvo skaičiuojamas nuo taško, kuris yra be galo nutolęs nuo krūvio, o tai turi aiškią fizinę reikšmę; logiška visada naudoti tą patį atskaitos tašką;
– sprendimas pasirodė sudėtingesnis.
5
(CT 2001 3 testas. A19). Plonas fiksuoto spindulio žiedas R tolygiai įkraunama, kad būtų įkrautas žiedo ilgio vienetas + γ .
Vakuume ant žiedo ašies per atstumą l nuo jo centro dedamas mažas rutulys su krūviu + q. Jei rutulys atleidžiamas, judėjimo metu jis įgis maksimalią kinetinę energiją, lygią
| 1) 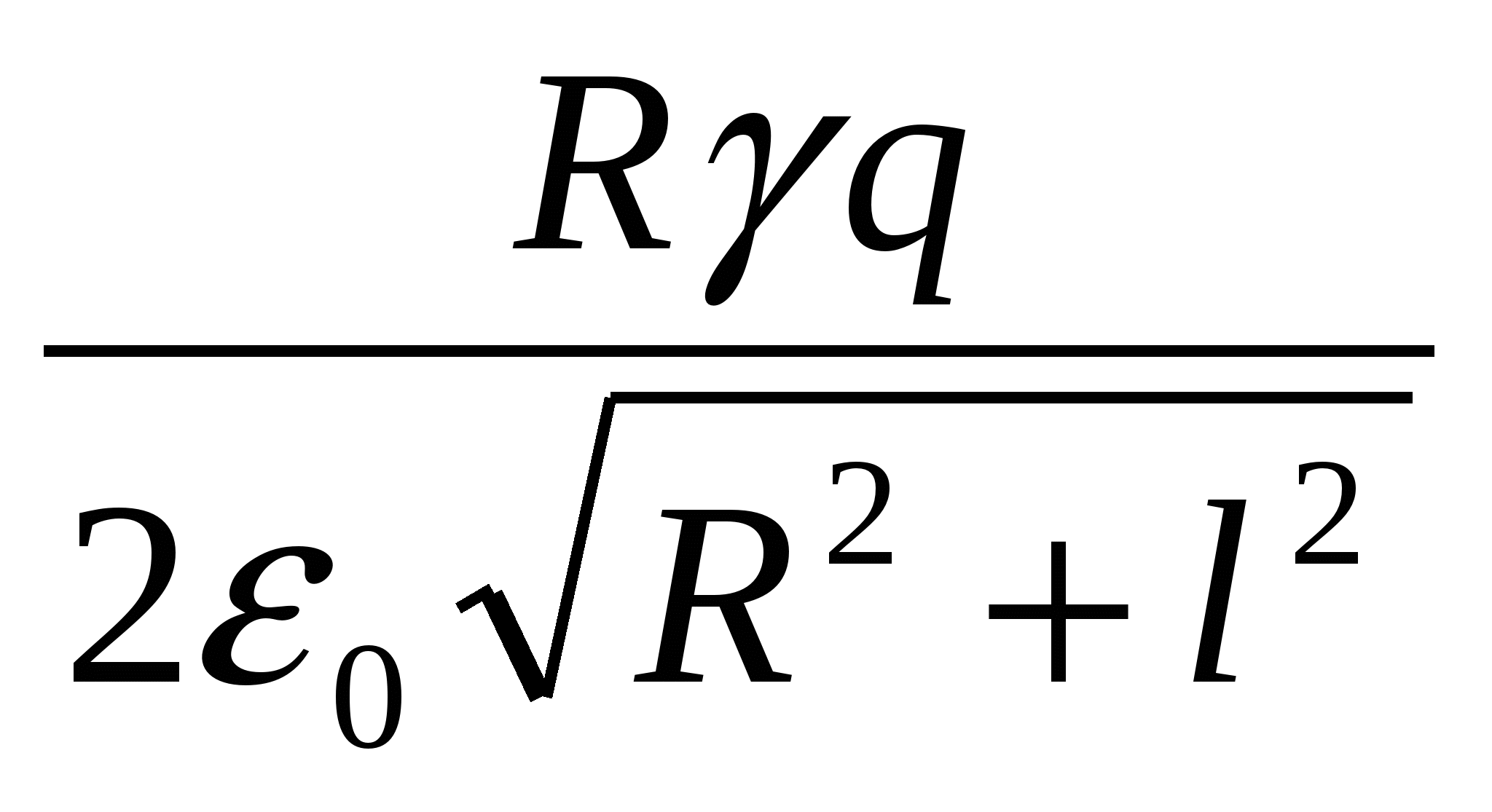 | 2) 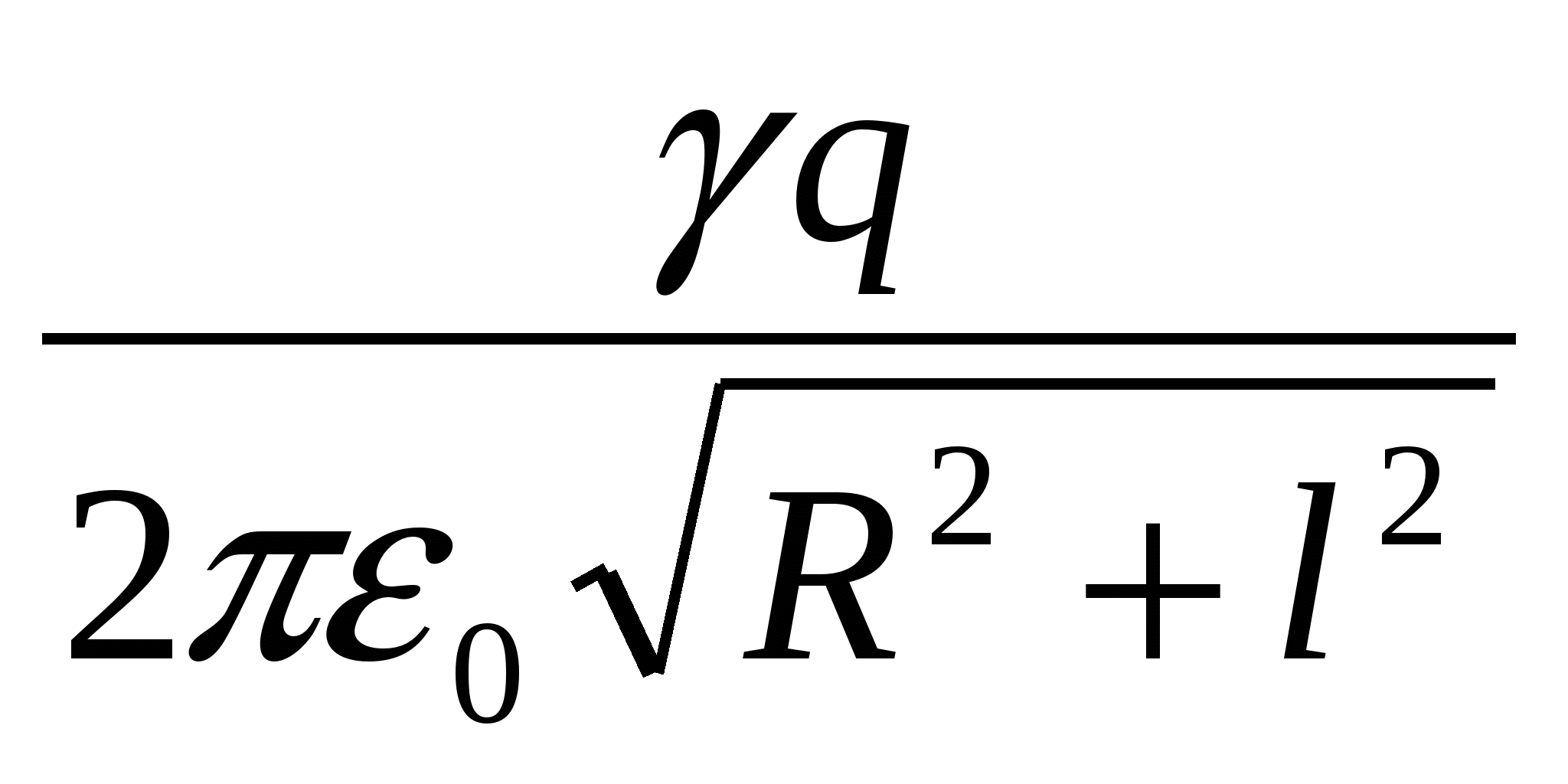 | 3)  |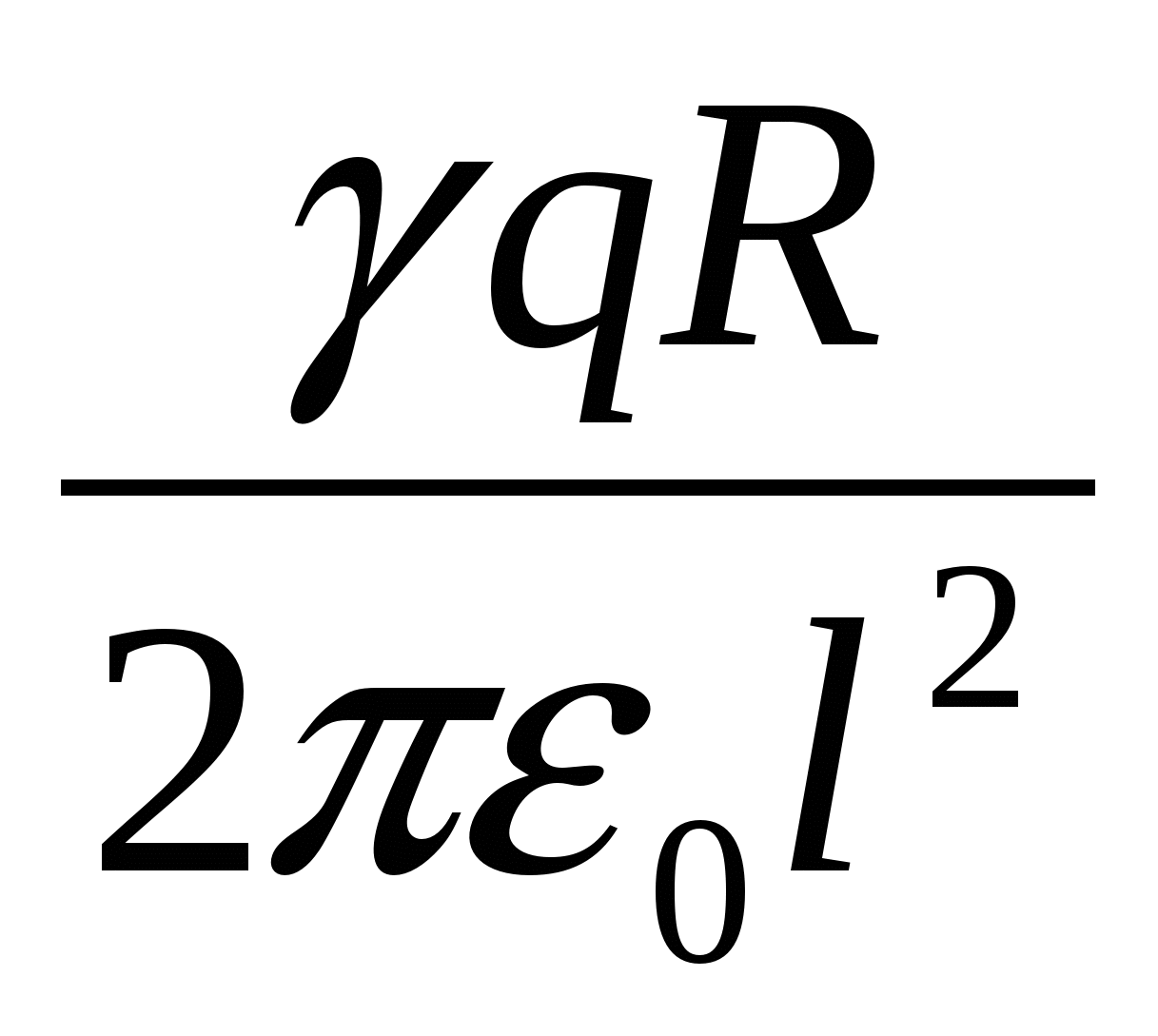
| 4) 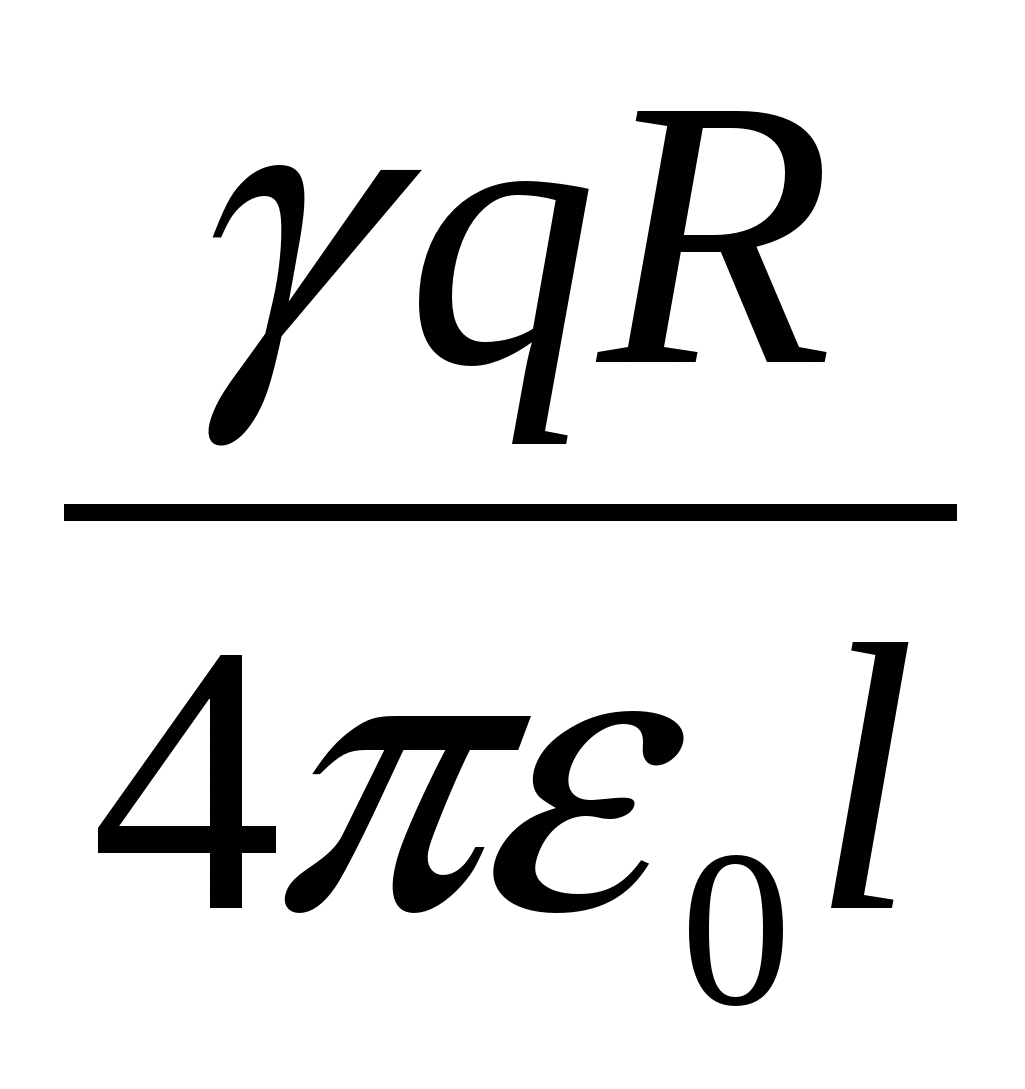 | 5)  |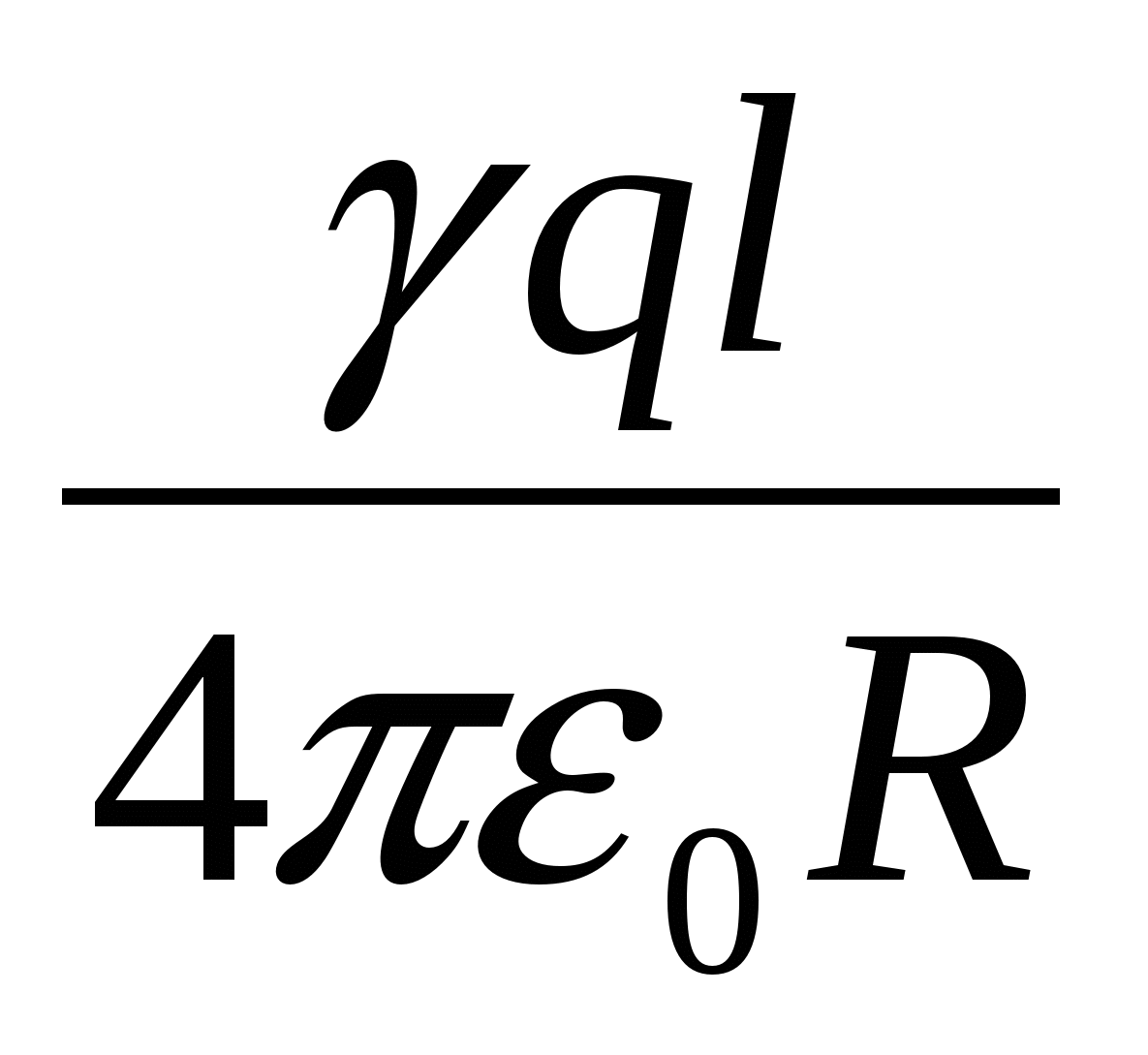
R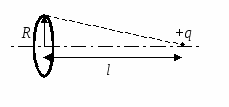 
sprendimas
Pagal energijos tvermės dėsnį E = U, kur U- sąveikos energija taškinis mokestis ir žiedai.
Tipiška klaida: sprendžiant šią problemą, manoma, kad dėl krūvio pasiskirstymo išilgai žiedo simetrijos galima jį „nutempti“ į žiedo centrą ir toje vietoje rasti žiedo kuriamo lauko potencialą. krūvio, kaip taškinio krūvio lauko potencialo: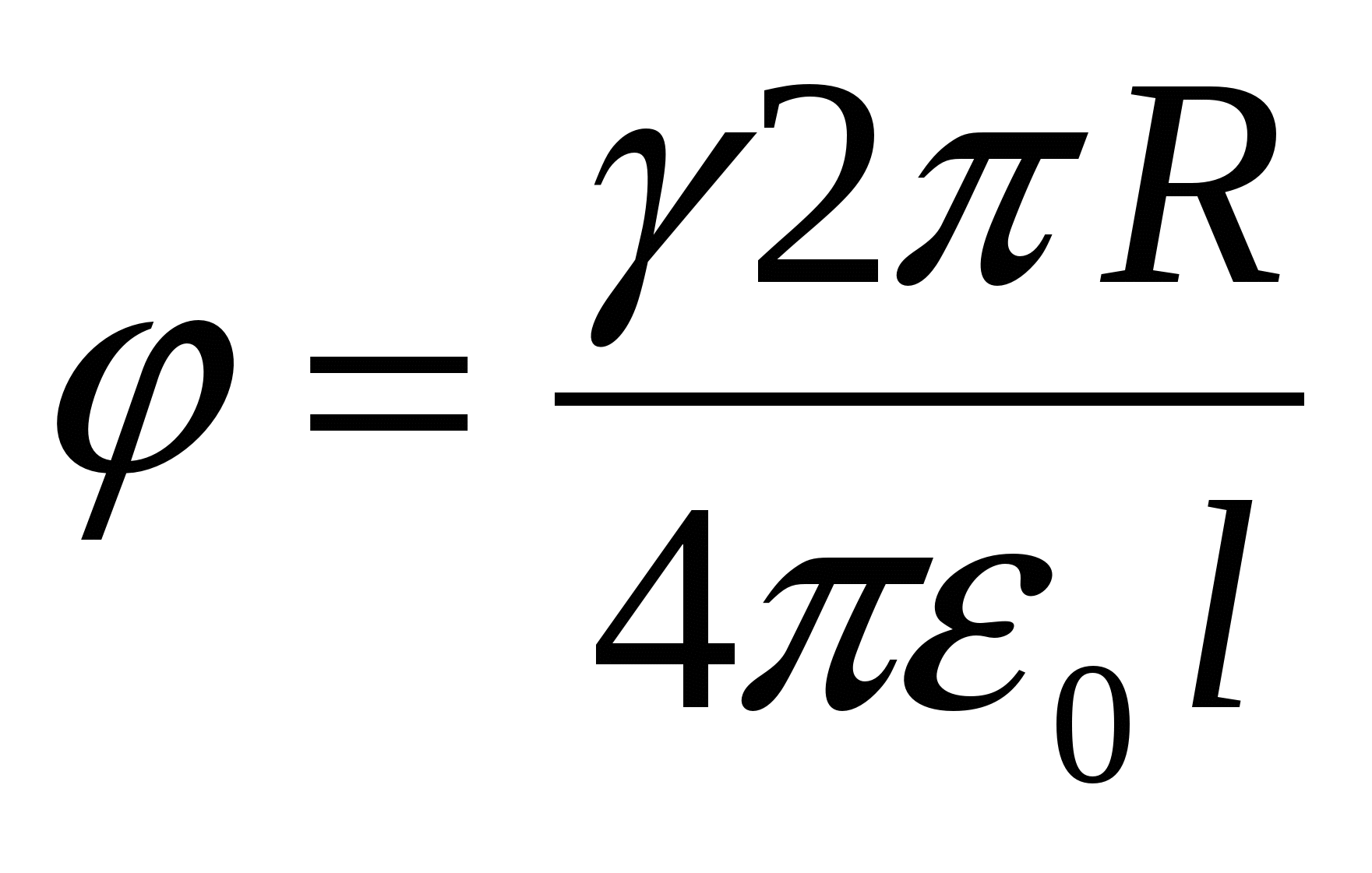 
. Tačiau to padaryti negalima, nes krūvio simetrija yra ne erdvinė, o plokštuma. Tiesą sakant, žiedą reikėtų suskaidyti į mažus elementus, į kuriuos galima atsižvelgti materialūs taškai, nustatykite kiekvieno tokio taškinio krūvio lauko potencialą krūvio vietoje + q
ir susumuokite rezultatus:
Žiedo sąveikos su krūviu energija ir didžiausia krūvio kinetinė energija yra lygios pagal energijos tvermės dėsnį: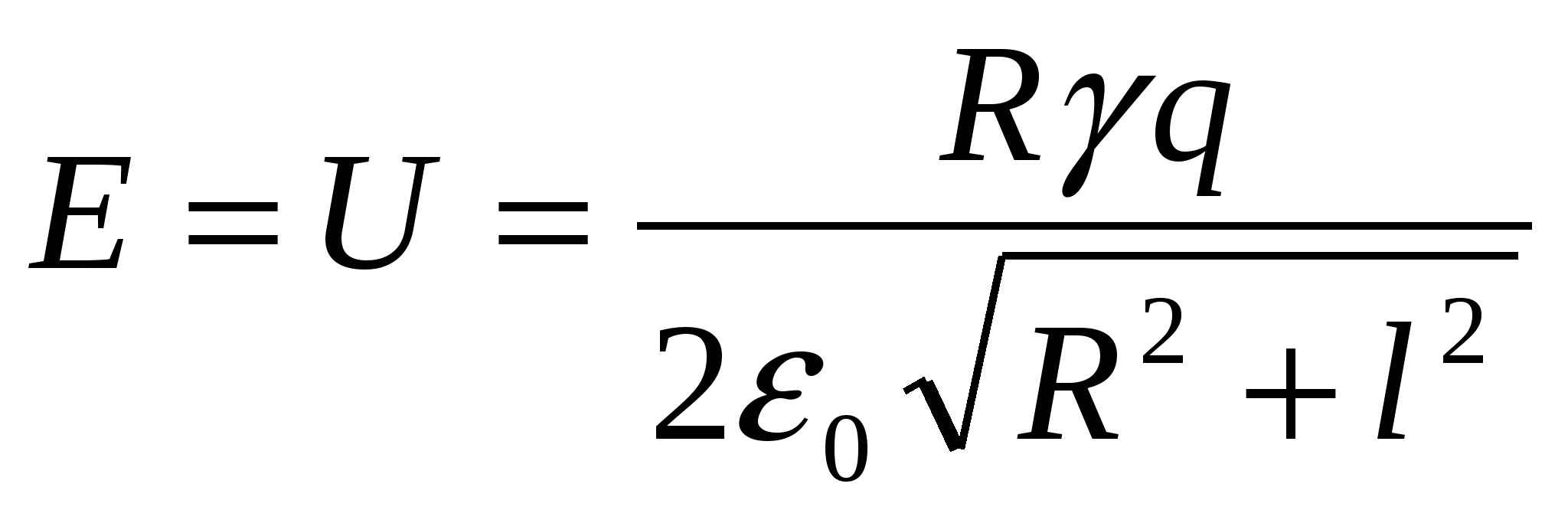 
– atsakyk.
Panašiai potencialas randamas ir sprendžiant uždavinį A 19 iš TsT 2001 testo Nr. 8: 10–9 C krūvis tolygiai paskirstomas ploname 3 cm spindulio vielos žiede. Nustatykite potencialų skirtumą tarp žiedo centro ir taško, esančio žiedo ašyje 4 cm atstumu nuo centro. Atsakymas: 120 V.
6
(TsT 2000 Test 3. A 20).Jei spindulio metalinis rutulys R
1
, įkrautas iki potencialo φ
1
, prijunkite plonas
viela su neįkrautu metaliniu spindulio rutuliu R
2, tada bendras junginio potencialas bus lygus
| 1) 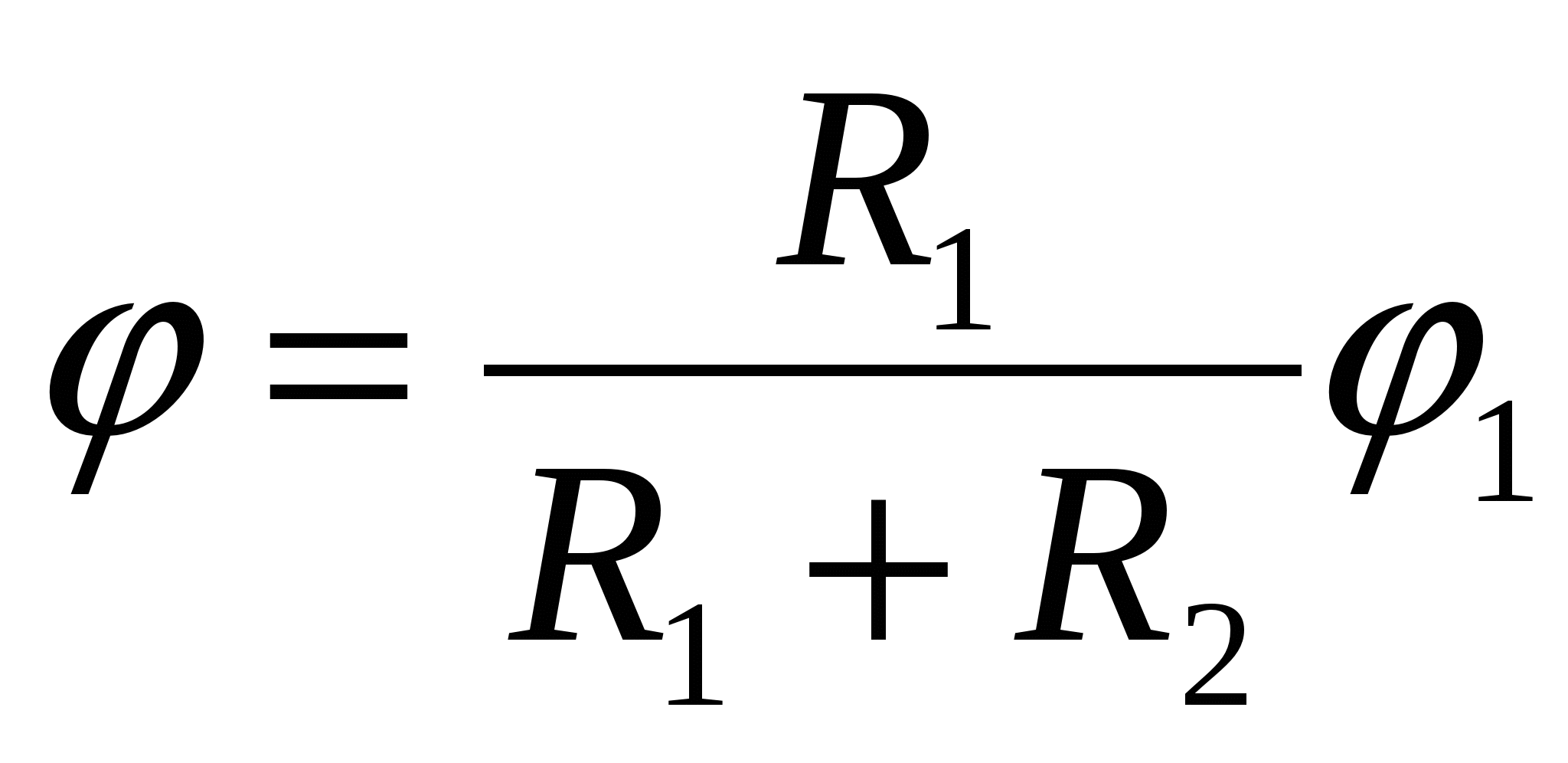 | 2) 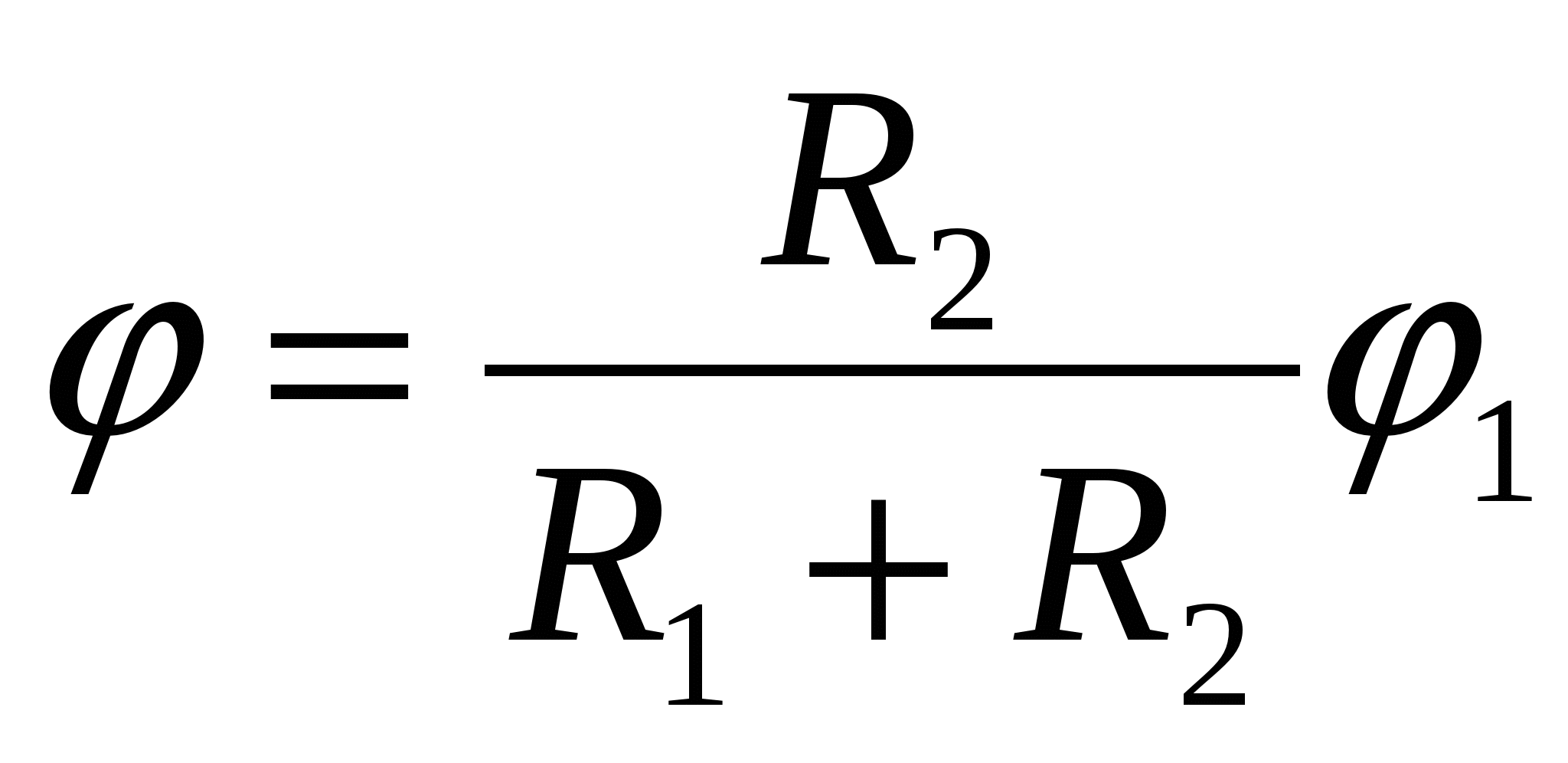 | 3)  |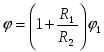
| 2) 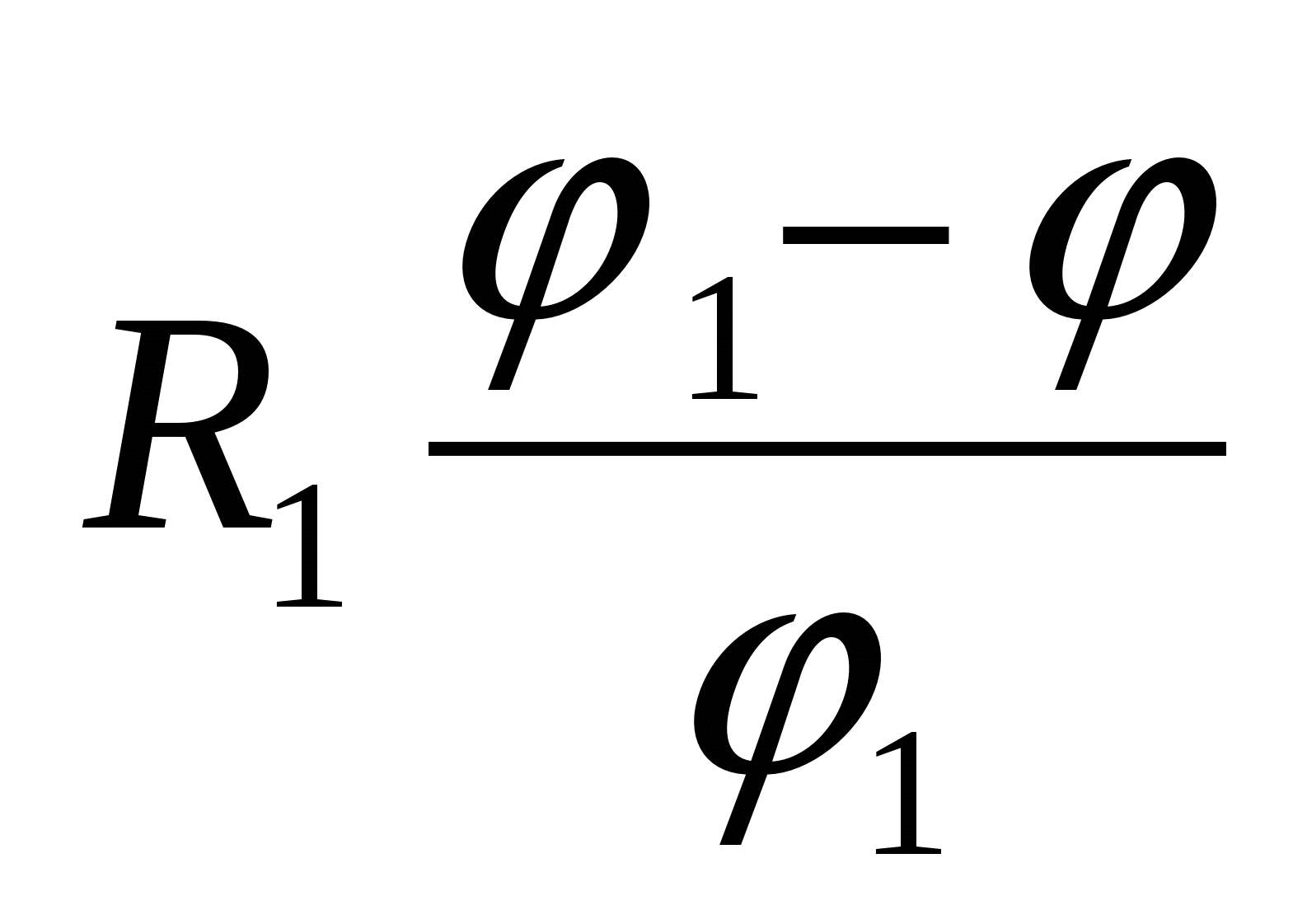 | 3)  |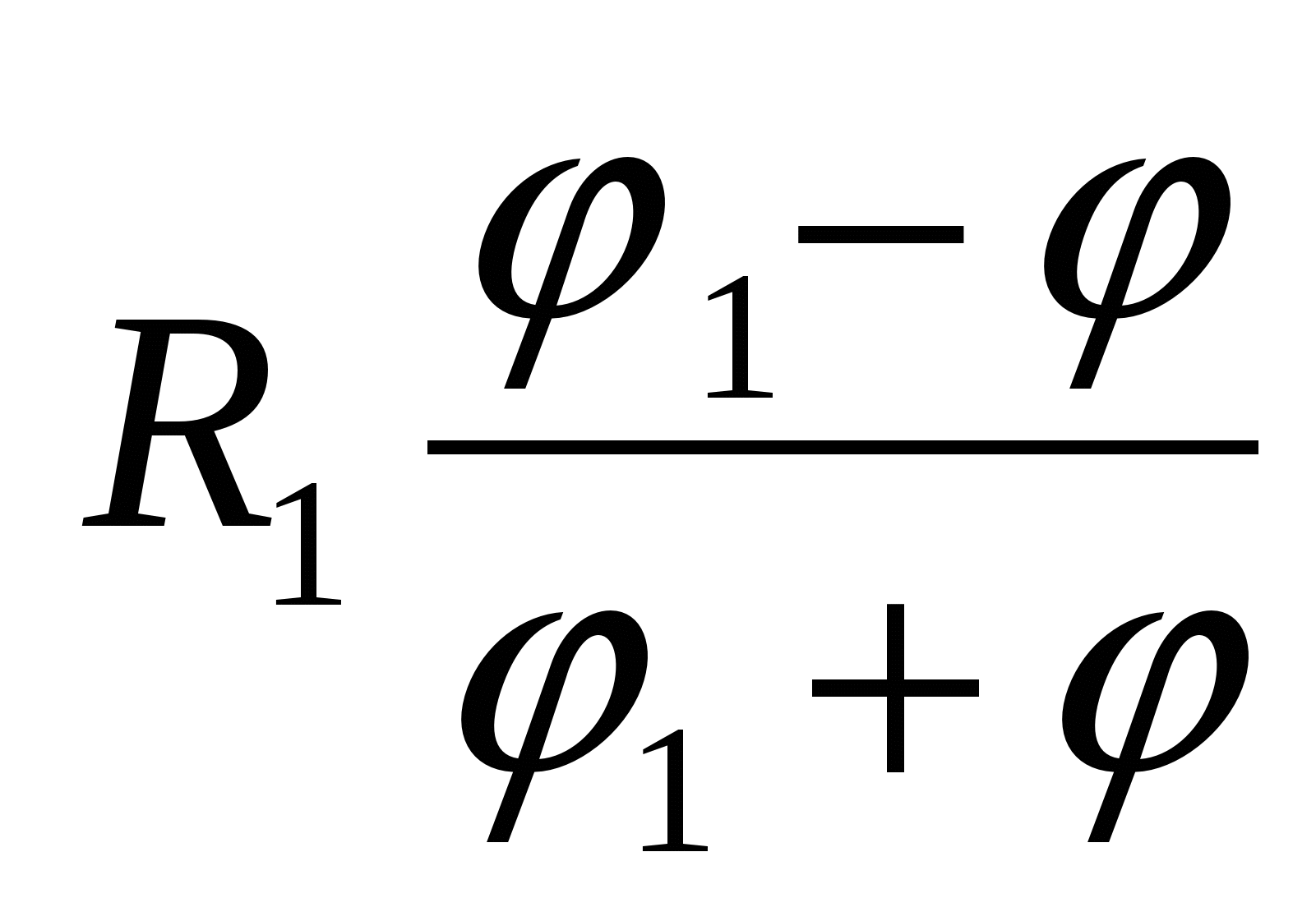
|
| 4) 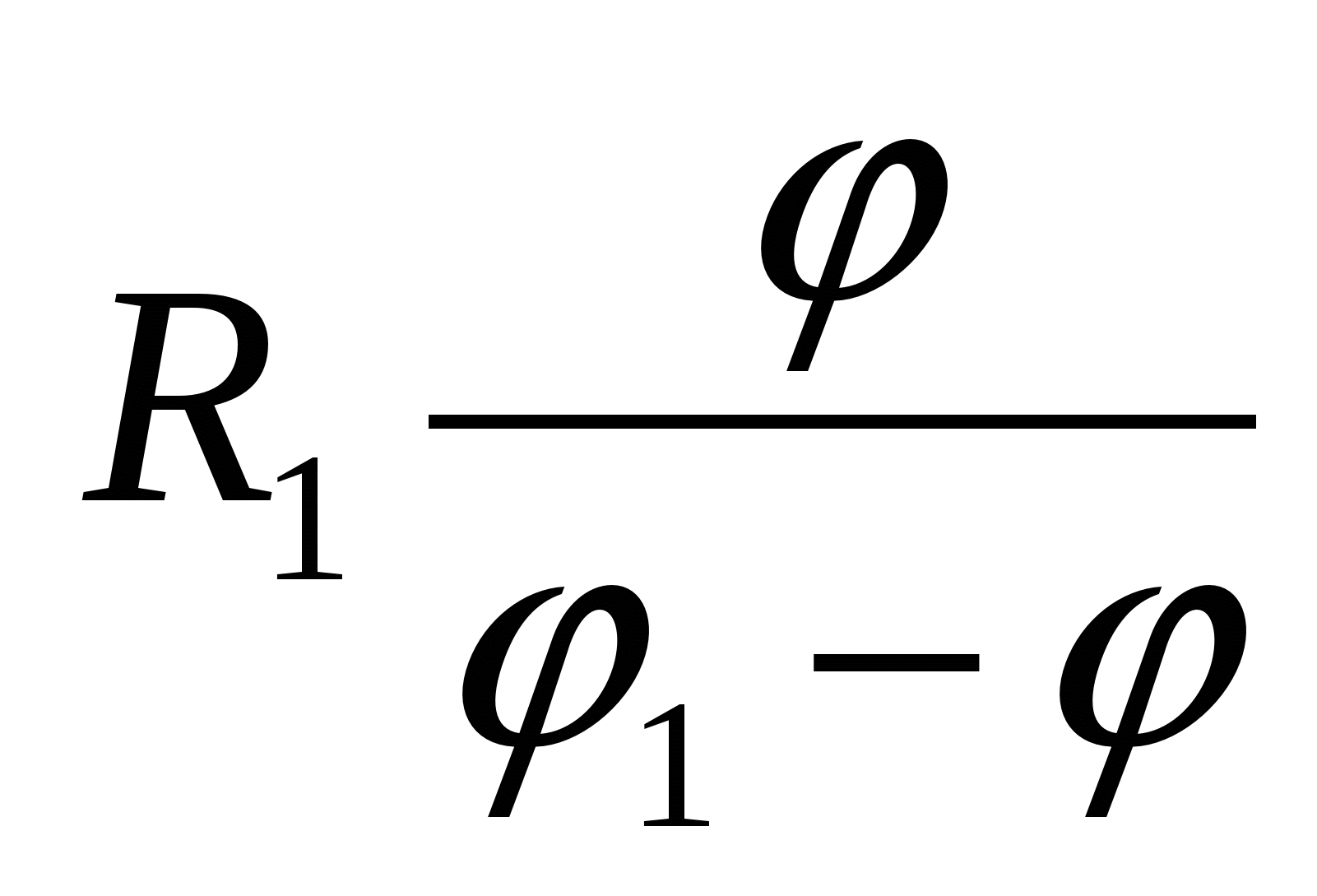 | 5)  |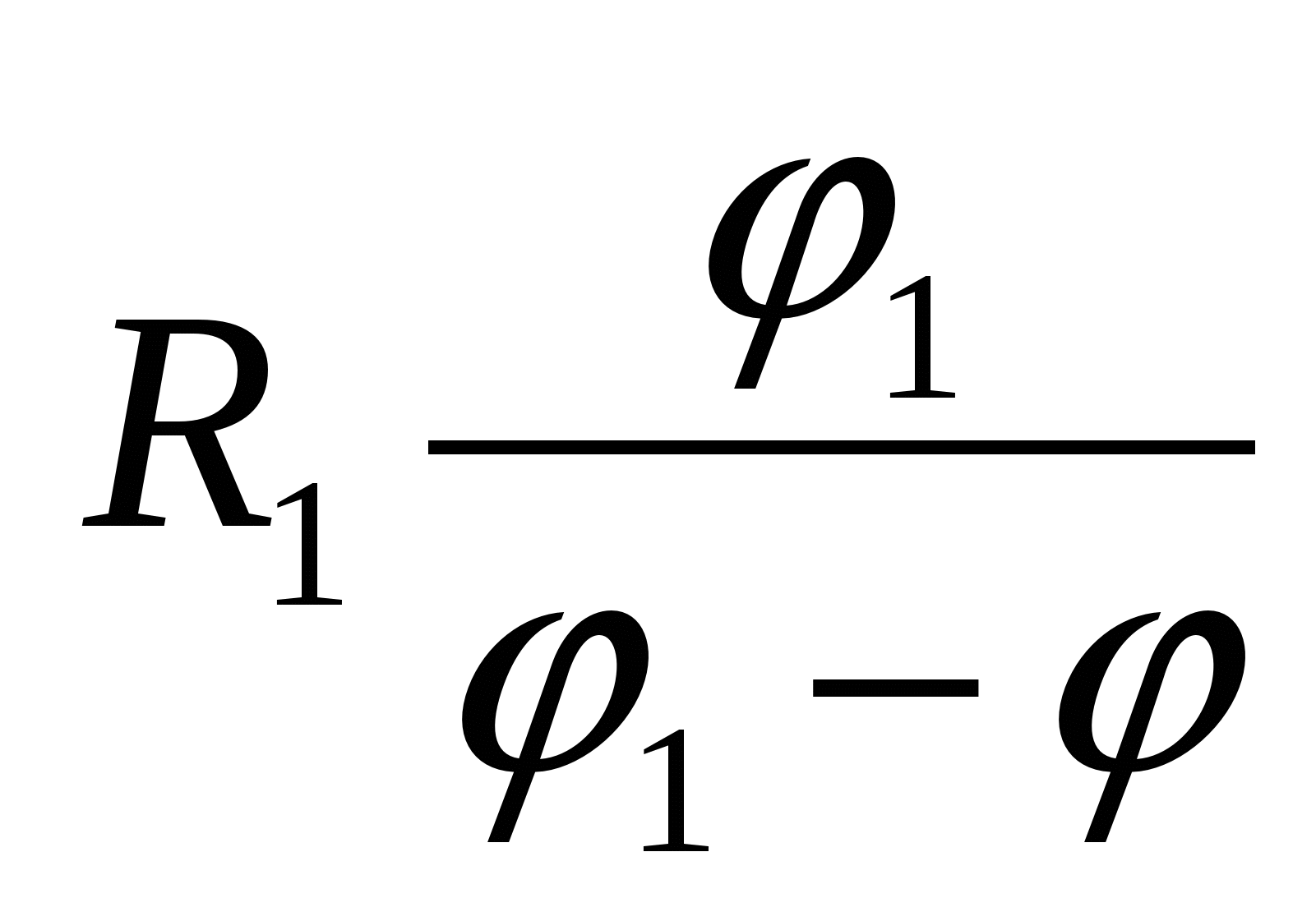
7
(CT 2001. 2 testas. A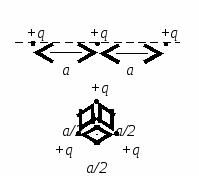 
19). Kiek darbo reikia padaryti, kad trys vienodi taškiniai teigiami krūviai q, esantis vakuume išilgai vienos tiesios linijos atstumu a
vienas nuo kito, išdėstyti lygiakraščio trikampio su kraštine viršūnėse a/2.
7.1. Yra du elektrodai koncentrinių rutulių su spinduliu pavidalu a(vidinis) ir b(išorinis). Tokia sistema vadinama sferiniu kondensatoriumi. Raskite bet kurio lauko taško tarp elektrodų potencialą.
7.2. Apskaičiuokite potencialą elektrinis laukas dipolis.
7.3. Raskite krūvių sistemos, esančios tiesinių matmenų tūryje, lauko potencialą l, atstumais .
7.4. Nubraižykite dviejų įkrautų sferų sistemos potencialų diagramą.
7.5. Apskaičiuokite spindulio rutulio lauko potencialą a, vienodai įkrautas tūriu: a) rutulio viduje; b) už kamuolio ribų. Paveikslėlių grafikas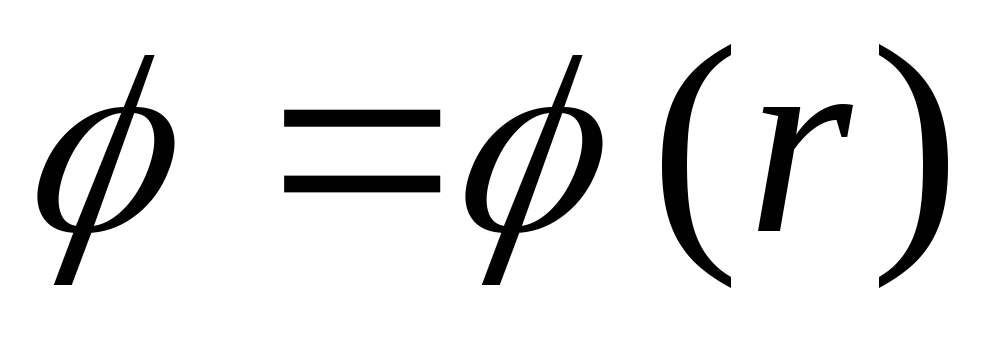 
, kur r yra atstumas nuo rutulio centro. Išspręskite problemą integruodami Puasono lygtį į sferines koordinates ir taip pat naudodami lauko stiprumo ir potencialo ryšį.
7.6. Išilgai plonos vielos žiedo spindulio R tolygiai paskirstytas krūvis q. Ištirkite elektrinio lauko potencialo priklausomybę nuo žiedo ašies nuo atstumo iki jo centro. Raskite įtampą kaip potencialų gradientą.
7.7. Sferos spindulys 
, vienodai įkrautas įkrovimu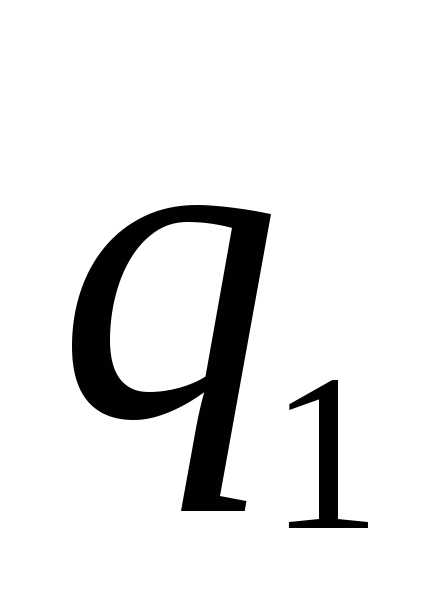 
, apsuptas plonu koncentriniu spindulio rutuliu 
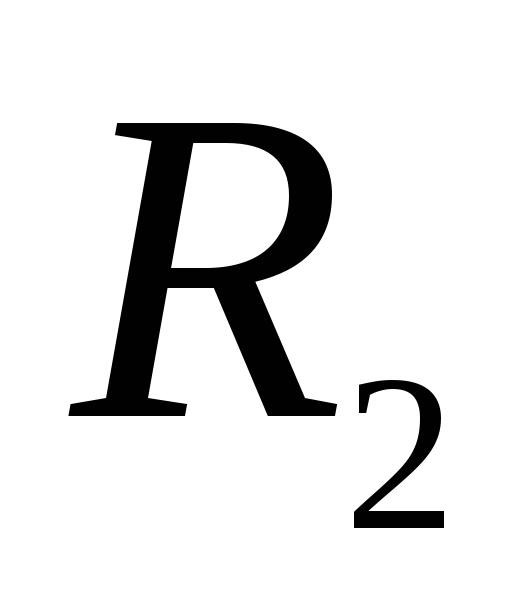. Koks mokestis 
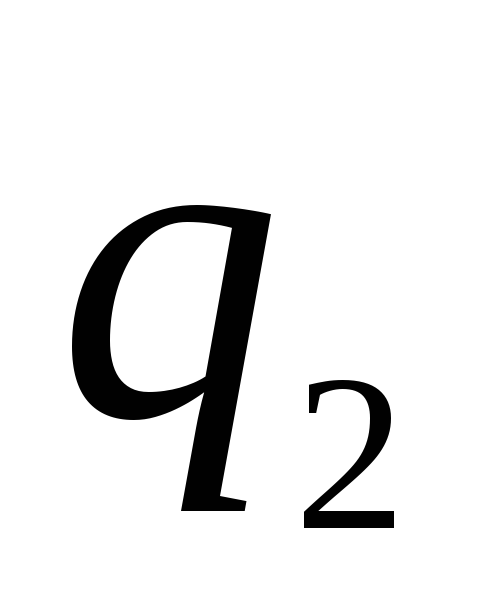reikia informuoti išorinę sferą, kad išnyktų vidinės sferos potencialas begalybės atžvilgiu? Įkrauti 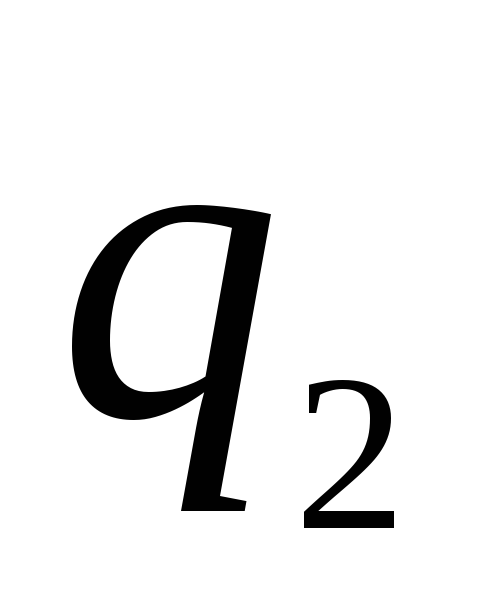taip pat tolygiai paskirstytas jo paviršiuje.
Problemų sprendimas
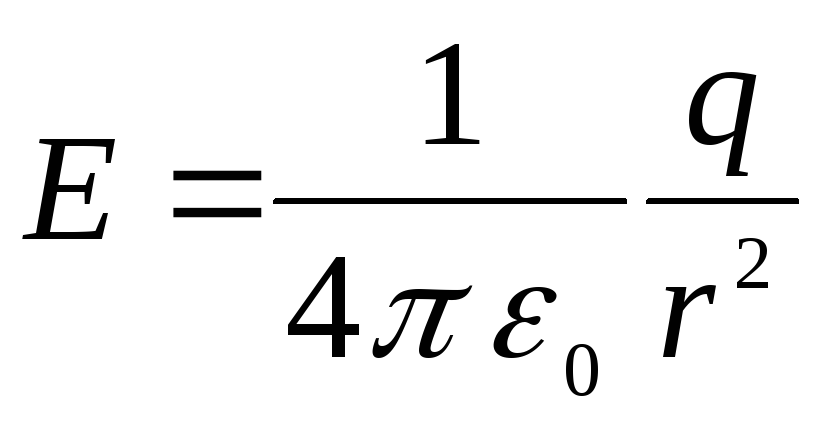
ir todėl erdvėje kinta taip pat, kaip ir taškinio krūvio lauko atveju, iš ko išplaukia, kad potencialų skirtumas tarp vidinės sferos ir bet kurio per atstumą nutolusio lauko taško r nuo kondensatoriaus centro, yra lygus
.
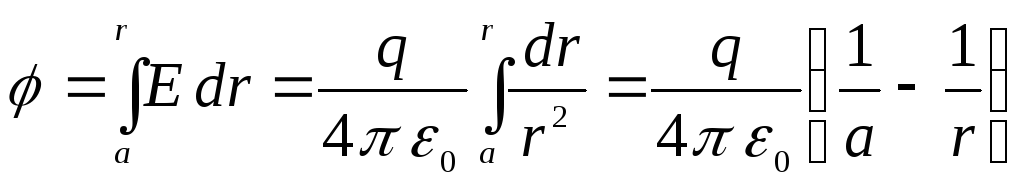Potencialus skirtumas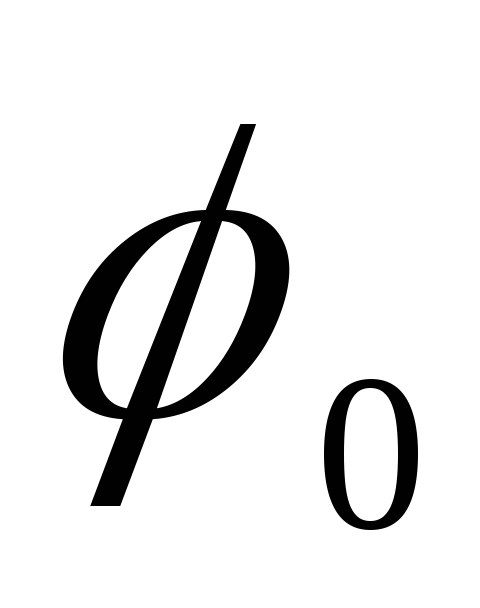 
tarp elektrodų (sferų) bus lygus
.
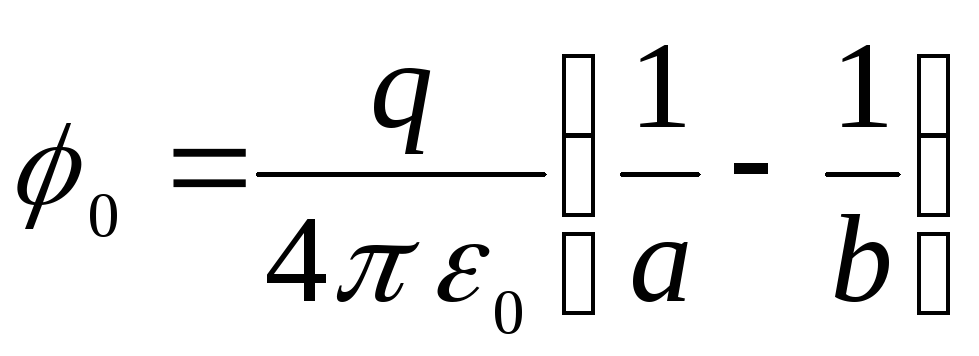Iš šių dviejų formulių seka
.
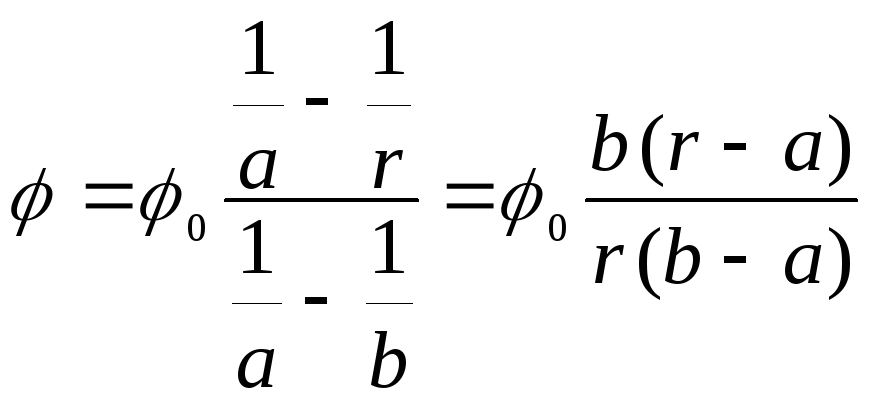Išmatavęs tarp elektrodų, galite apskaičiuoti bet kurio lauko taško potencialą.
7.2. Tegul mokesčių sistema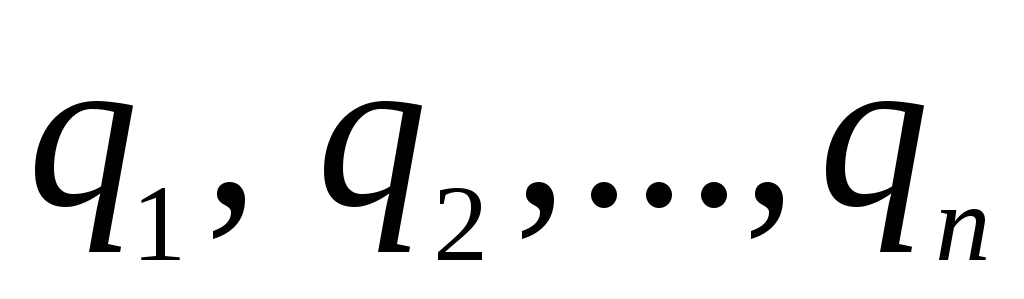 
yra tūryje, kurio linijiniai matmenys l. Raskime šios krūvių sistemos sukurto lauko potencialą atstumais r, kurie yra dideli, palyginti su l. Mes pasirenkame koordinačių O pradžią tūryje, kurį užima krūvių sistema, ir nustatome krūvių padėtį naudodami spindulius - vektorius 
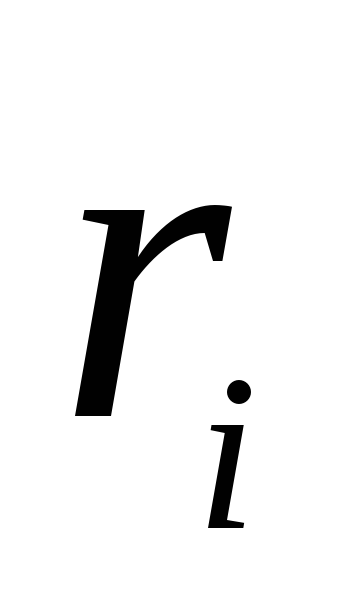(___ pav. rodomas vienas iš spindulio vektorių 
mokestis). Potencialas taške, kurį nustato spindulio vektorius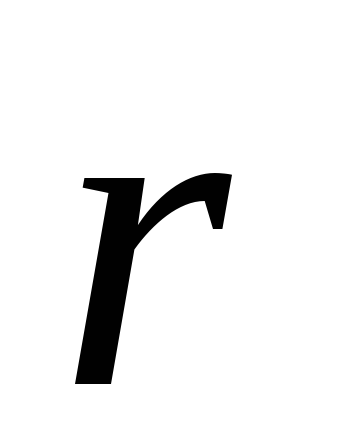 
, yra lygus
.
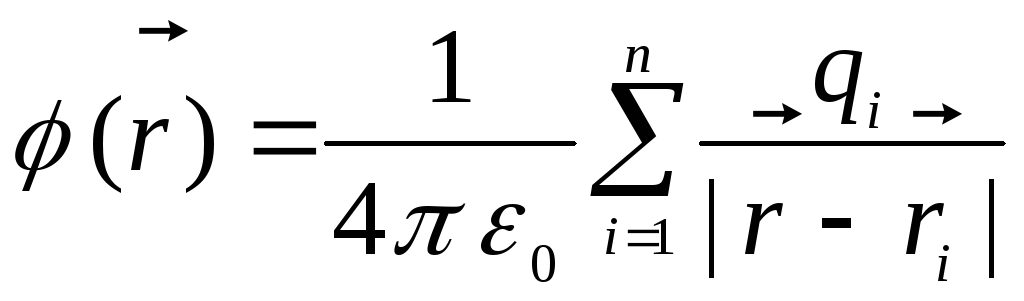Nes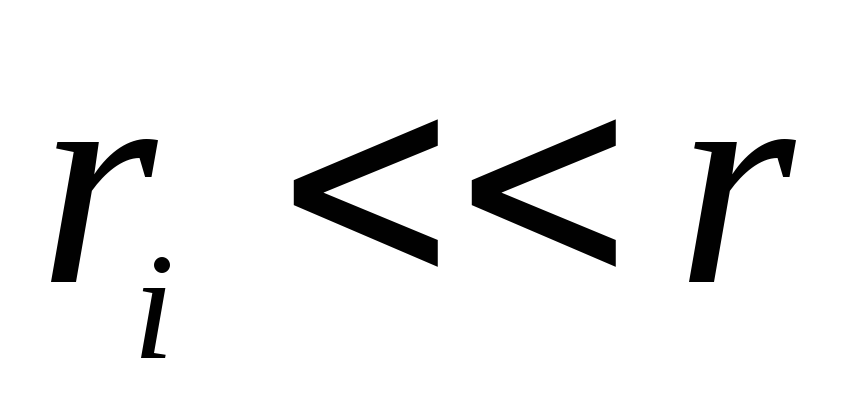 
, tada galime tai įdėti
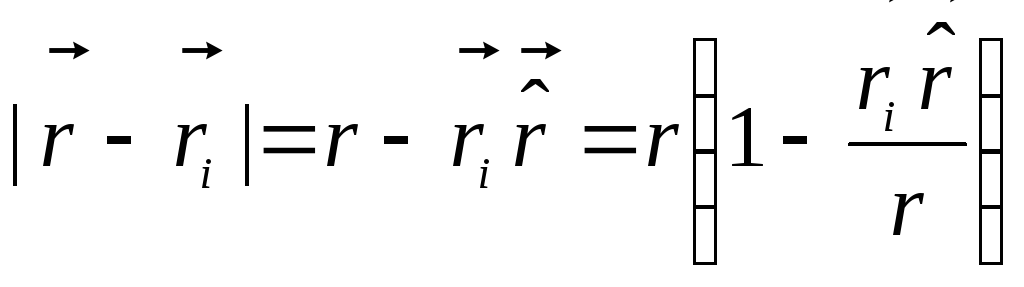
(simbolis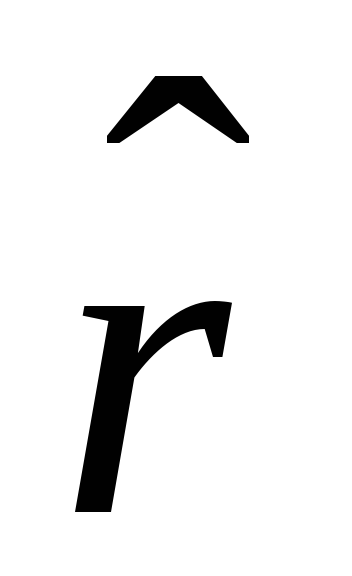 
pažymėjome vieneto vektorių). Tada
.
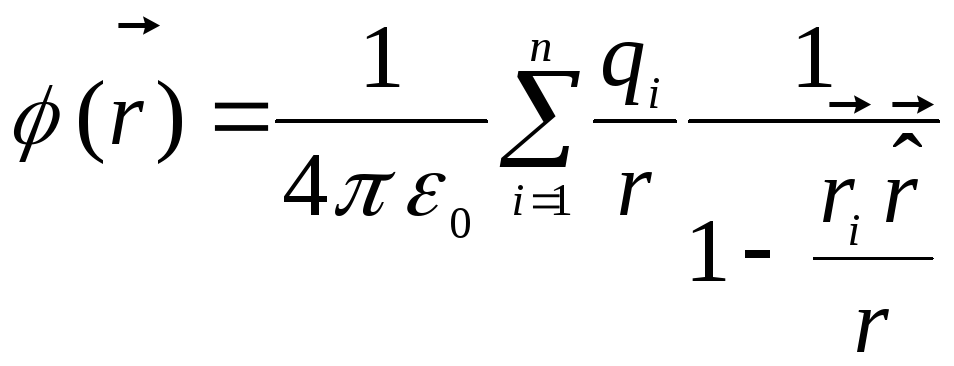Pasinaudokime formule
adresu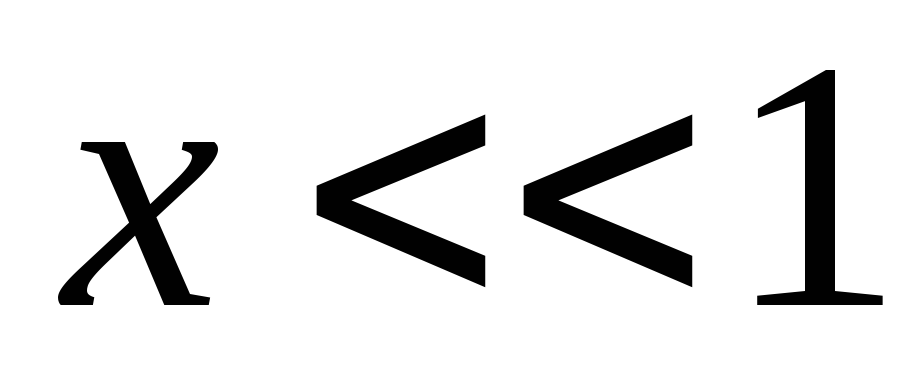 
.
Dabar galime rašyti
Pirmasis šios išraiškos narys yra taškinio krūvio lauko potencialas su reikšme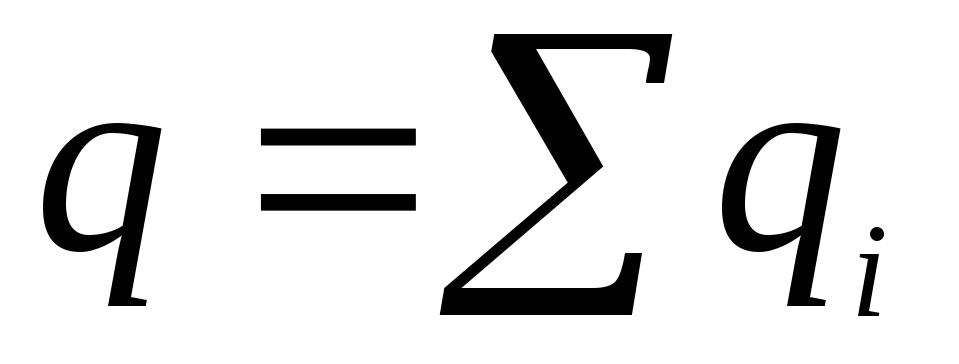 
. Antrasis terminas yra tos pačios formos, kaip ir išraiška, apibrėžianti dipolio lauko potencialą. Dipolio elektrinio momento vaidmenį atlieka kiekis
,
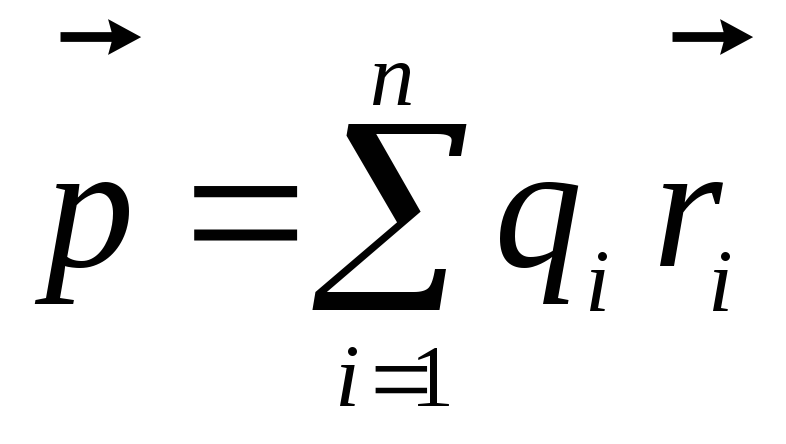kuris vadinamas krūvių sistemos elektriniu dipoliu momentu.
7.3. Jei lauką sukuria keli krūviai, tai šio lauko potencialas yra lygus atskirų krūvių sukuriamų laukų potencialų sumai
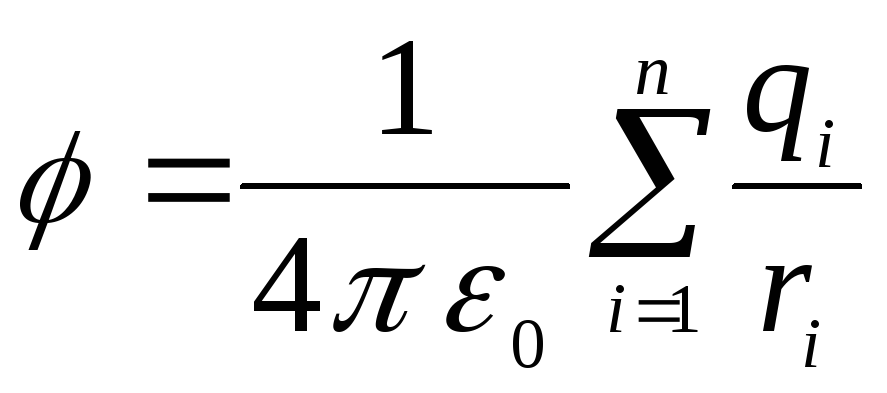
Čia 
yra gauto lauko potencialas nagrinėjamame taške begalybės atžvilgiu,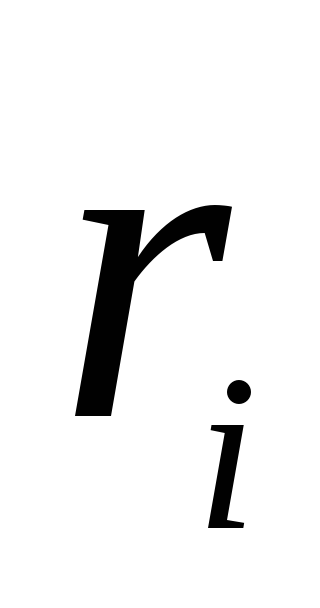 
yra atstumas nuo šio taško iki 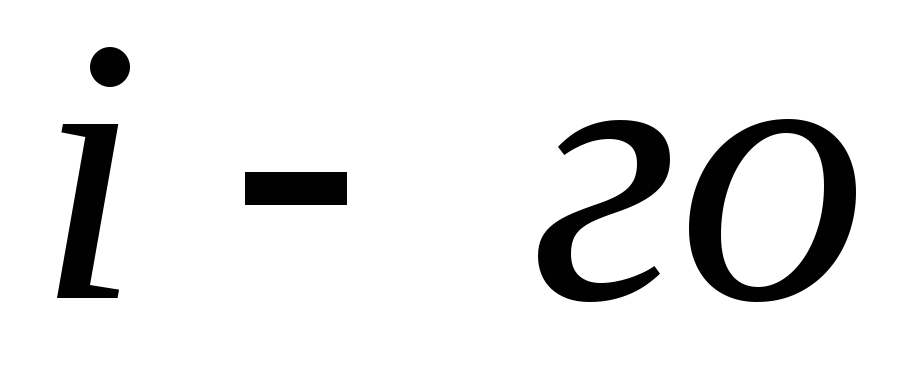įkrovimas, o sumavimas atliekamas per visus taškinius įkrovimus.
Nagrinėjamas laukas turi ašinę simetriją, todėl lauko modelis bet kurioje plokštumoje, einančioje per dipolio ašį, bus vienodas, o vektorius 
slypi šioje plotmėje. Taško M padėtis dipolio atžvilgiu bus apibūdinama naudojant spindulio vektorių 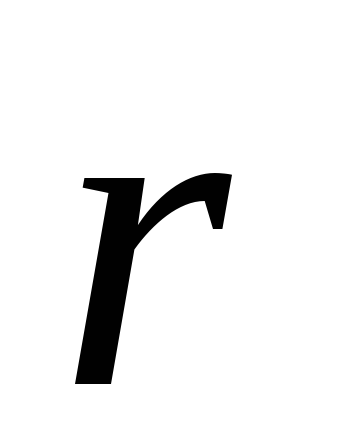, arba naudojant polines koordinates r ir 
. įkrovimo padėtis 
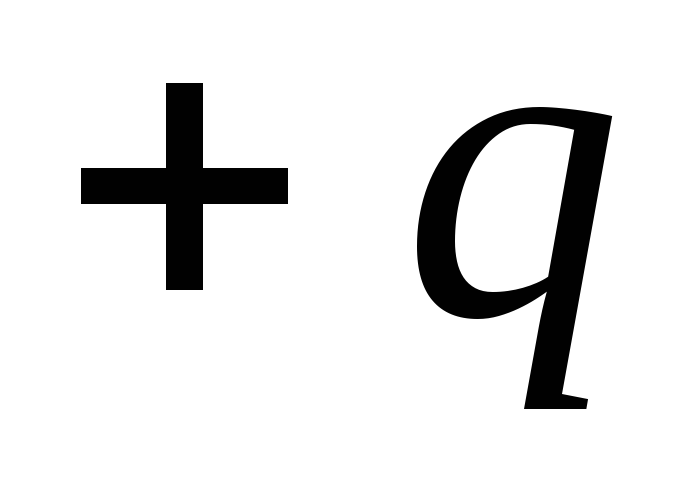dipolio centro atžvilgiu apibrėžia vektorius 
, ir mokestis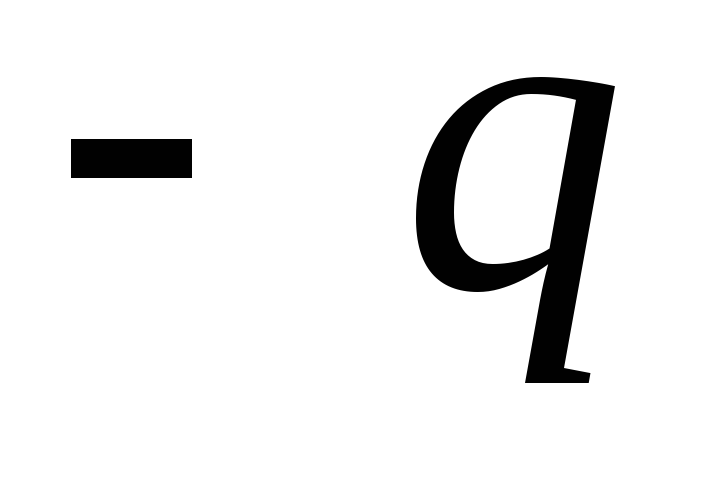 
– vektorius 
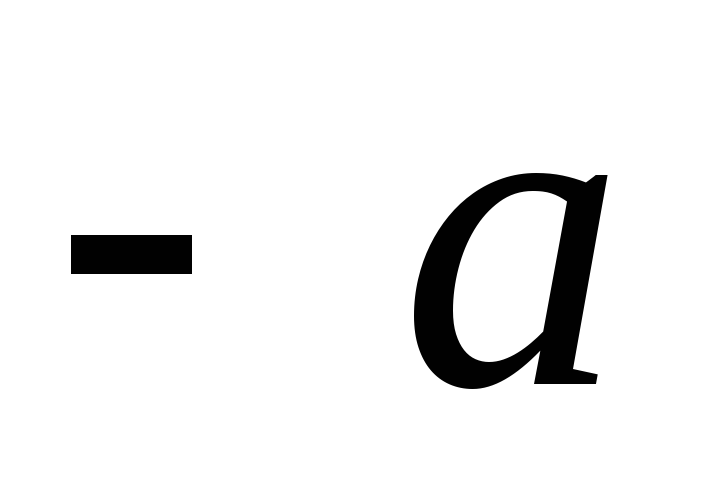. Tai akivaizdu 
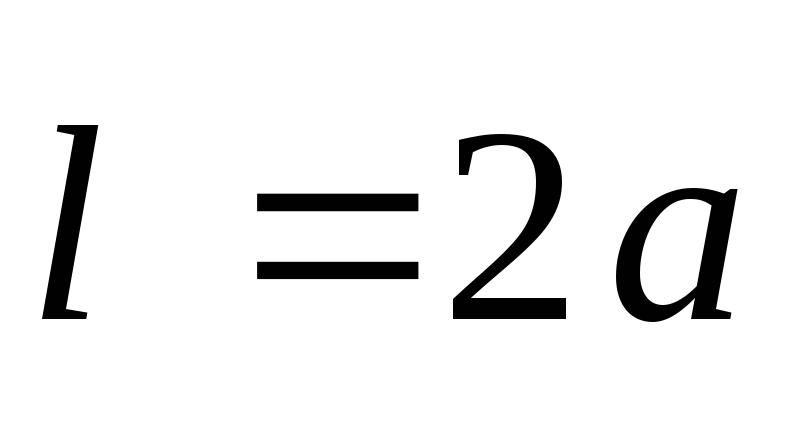, kur 
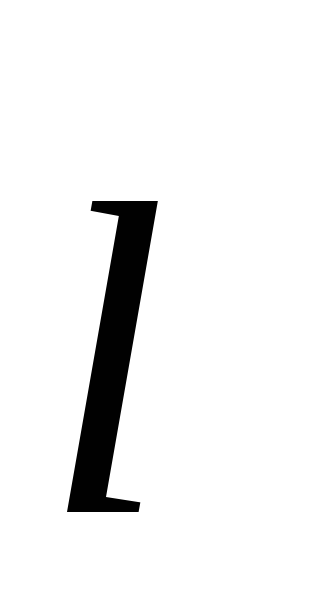yra dipolio ranka. Atstumai nuo mokesčių 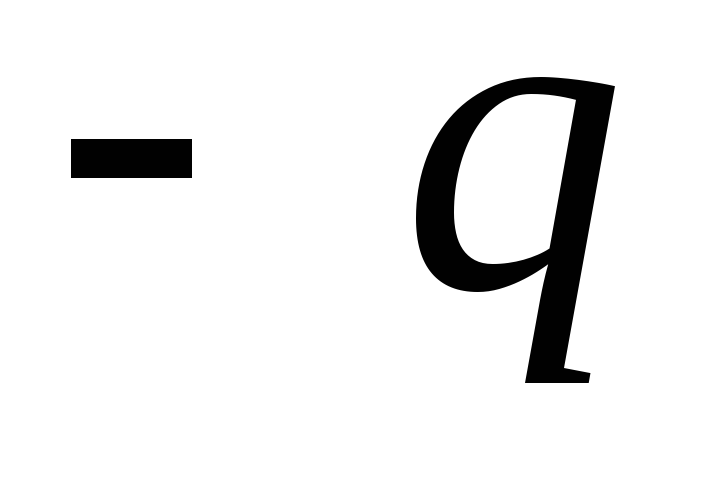ir 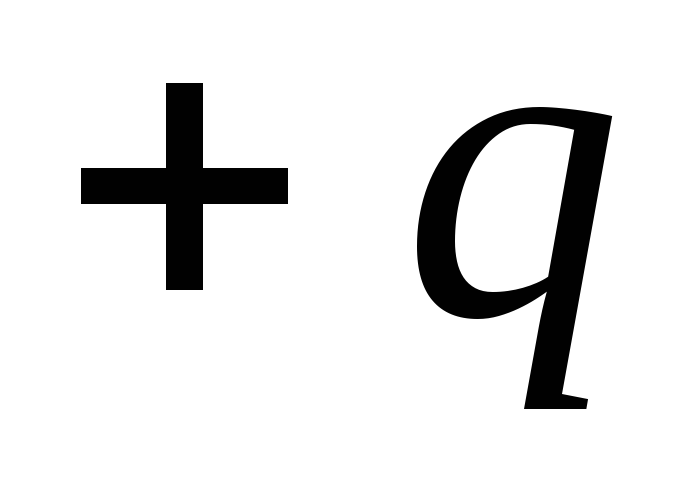iki pasirinkto taško M pažymime atitinkamai, 
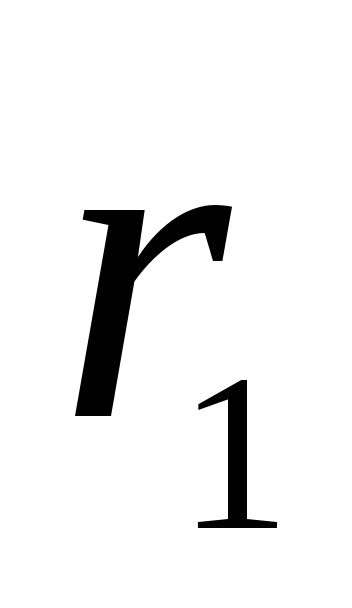ir 
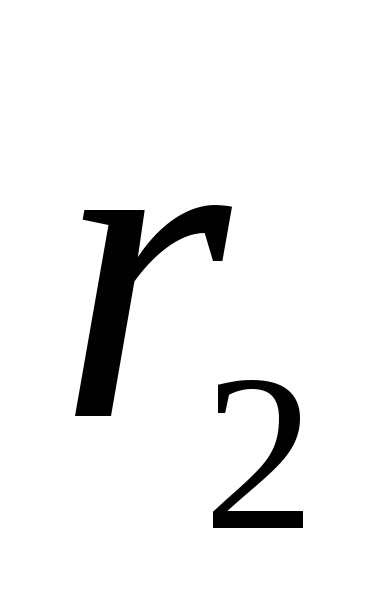. Nes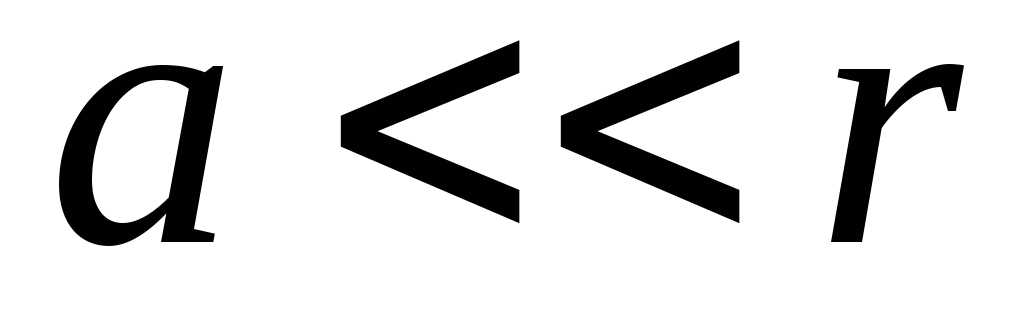 
, tada galime tai įdėti
Potencialas taške, kurį nustato spindulio vektorius 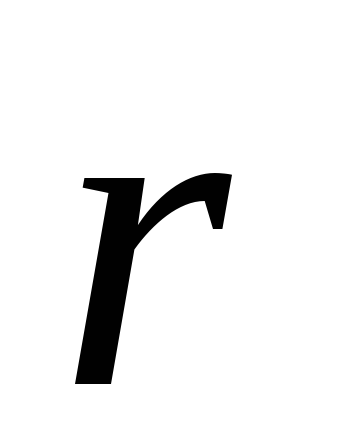, yra lygus
.
Darbas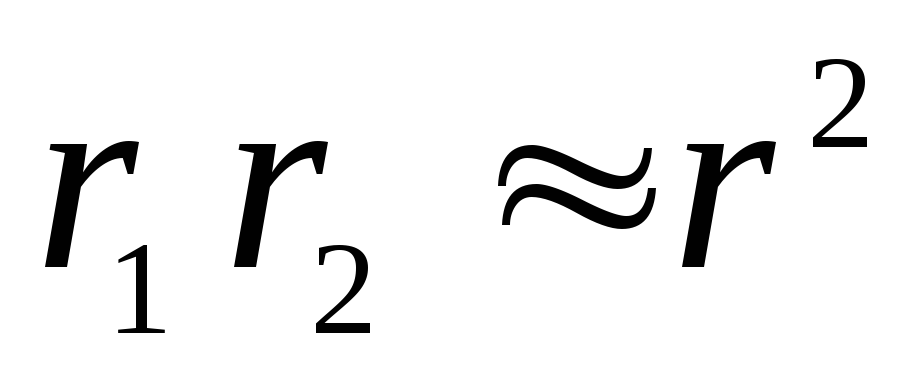 
, skirtumas 
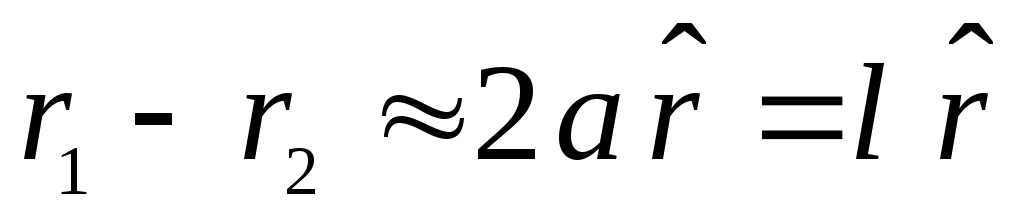. Vadinasi,
,
kur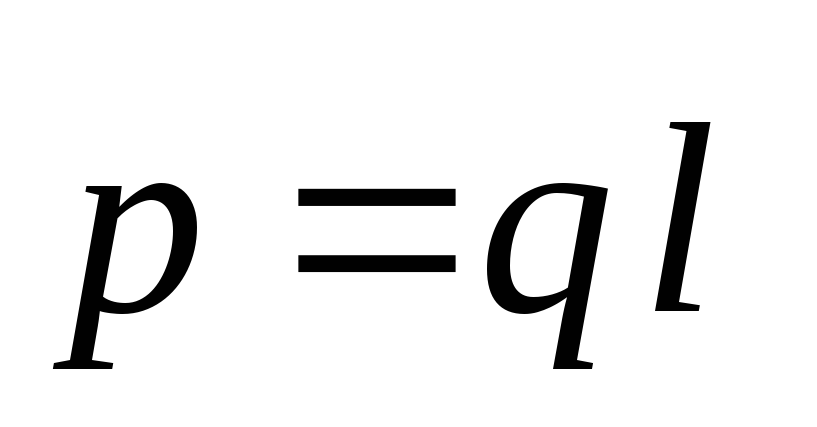 
yra dipolio elektrinis momentas.
Iš šios formulės matyti, kad dipolio lauko potencialą lemia jo elektrinis momentas. Lyginant dipolio lauko potencialą su taškinio krūvio lauko potencialu, matyti, kad dipolio lauko potencialas mažėja didėjant atstumui greičiau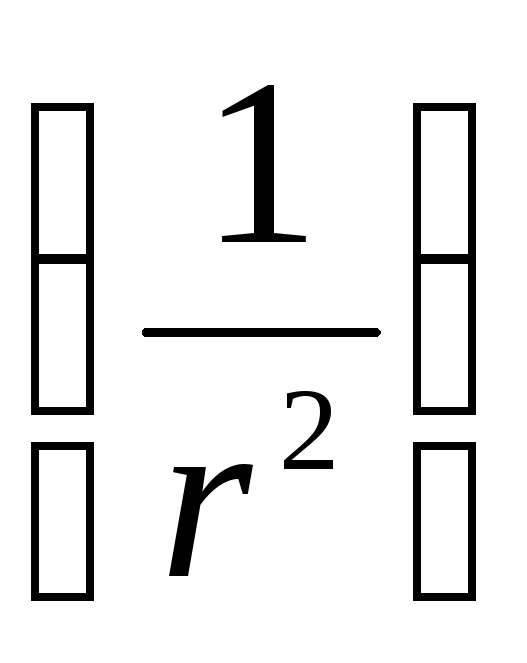 
nei taškinio krūvio lauko potencialas 
.
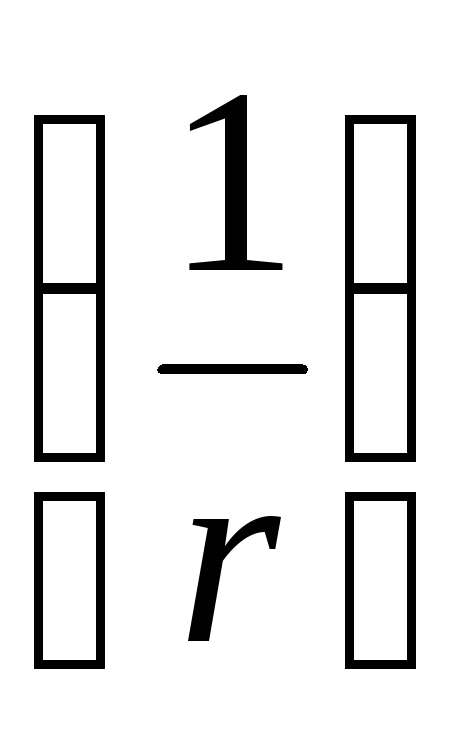Tai rodo ___ paveikslas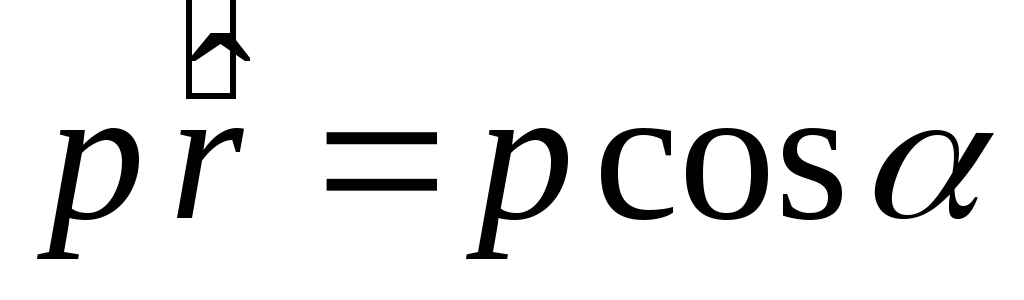 
. Štai kodėl
.
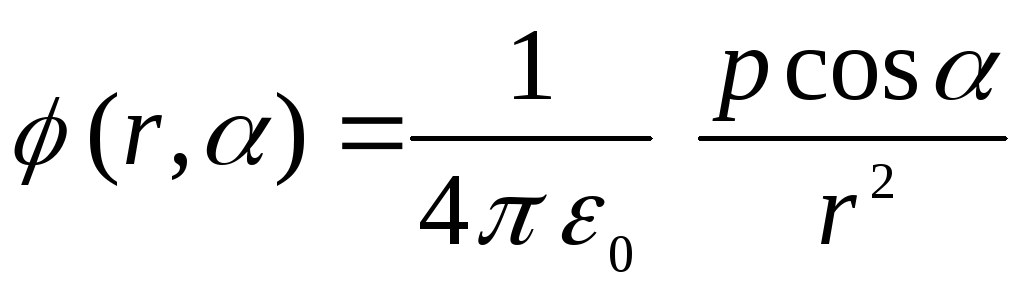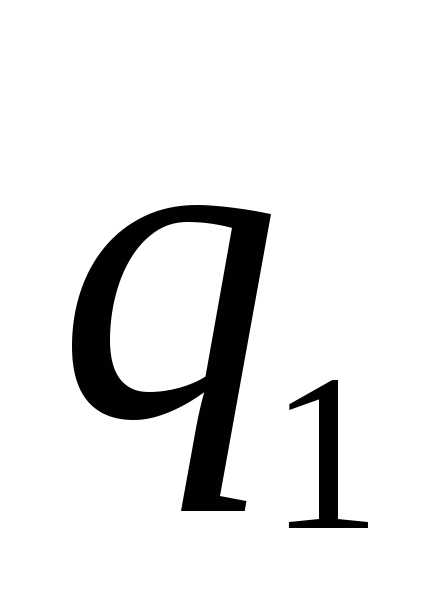7.4. Tegul vidinė sfera, kurios spindulys , turi teigiamą krūvį , o išorinis su spinduliu 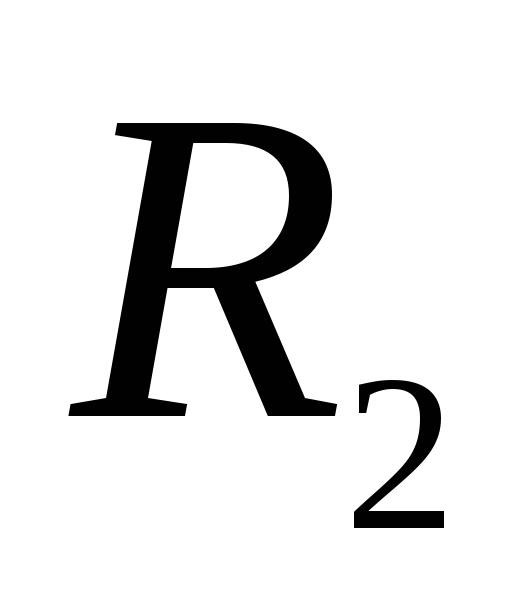- neigiamas krūvis 
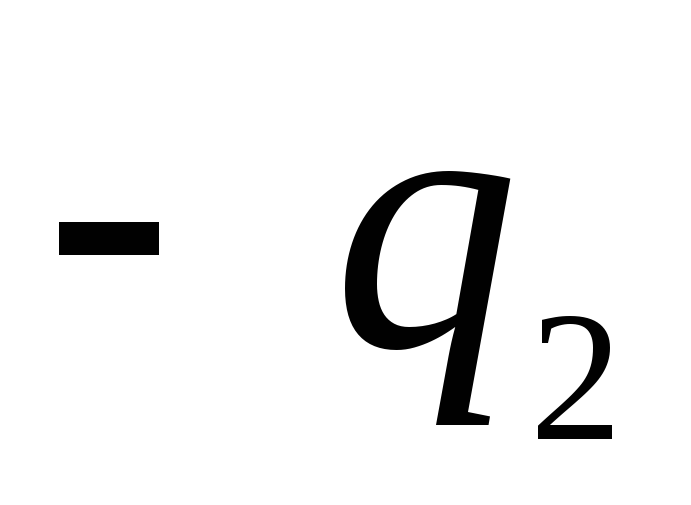, ir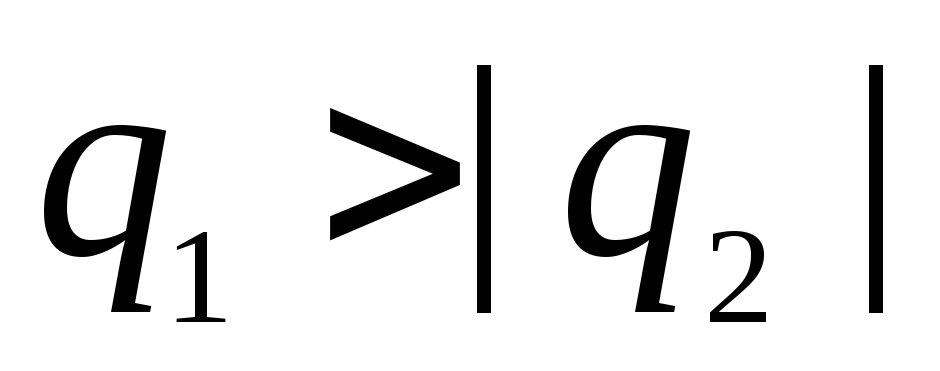 
.
Už sferų ribų potencialas bus lygus
,
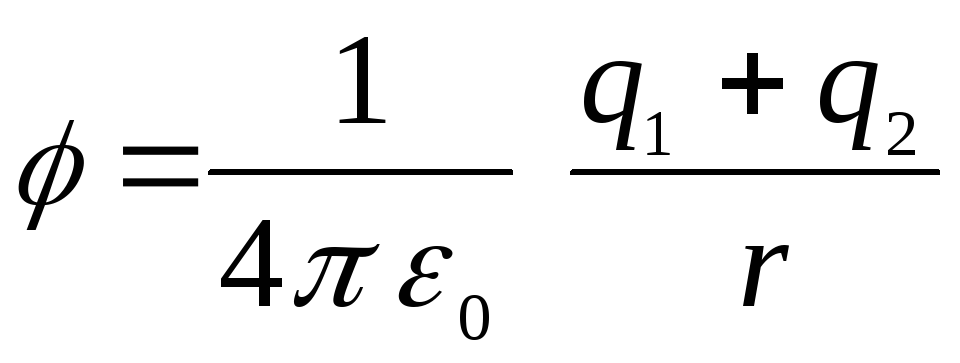kadangi jį kartu sukuria abi sferos (potencialas – išorinių jėgų darbas, atliekamas vienetiniam teigiamam krūviui judant iš begalybės į tam tikrą lauko tašką). Vienetinio teigiamo krūvio perkėlimas iš begalybės į plotą tarp sferų bus lygus dviejų darbų sumai: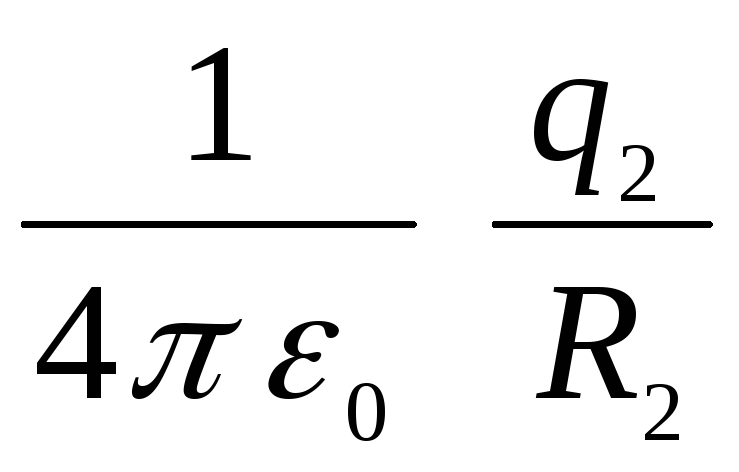 
(dirbti prieš jėgas, veikiančias iš išorinės sferos kelyje iš begalybės į jos paviršių) ir 
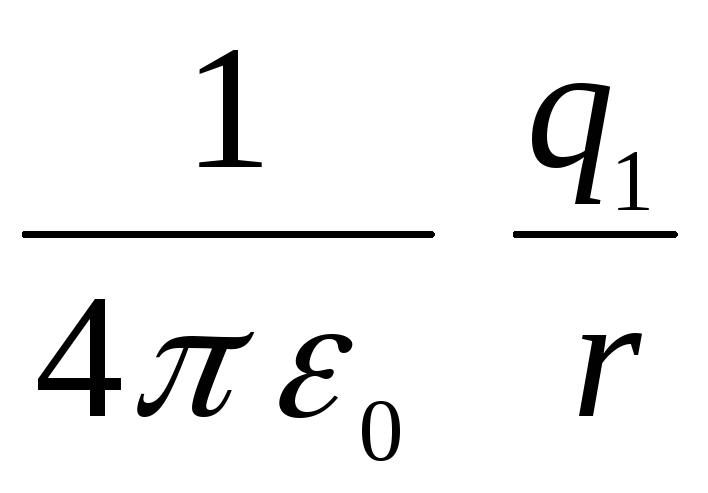(darbas prieš vidinės sferos lauką), t.y.
.
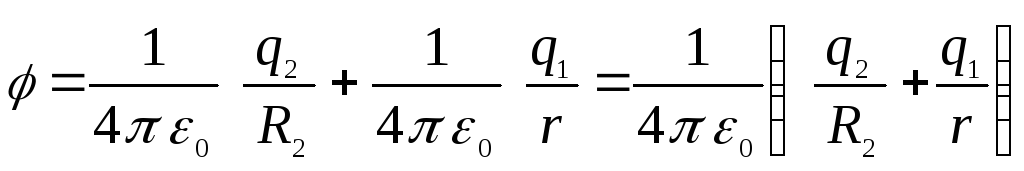Mažesnės sferos viduje potencialas bus pastovus ir lygus
.
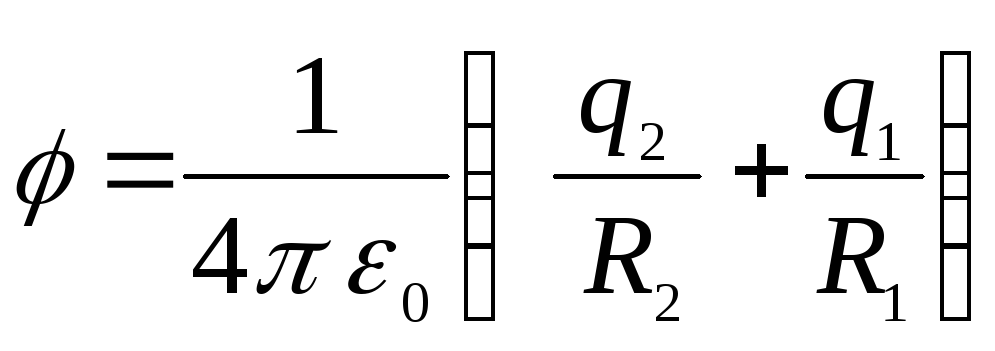Grafas, sudarytas pagal pirmą ir antrą formules, parodytas ____1 paveiksle.
Jei sferų krūviai yra vienodi dydžiu ir priešingi ženklu, t.y.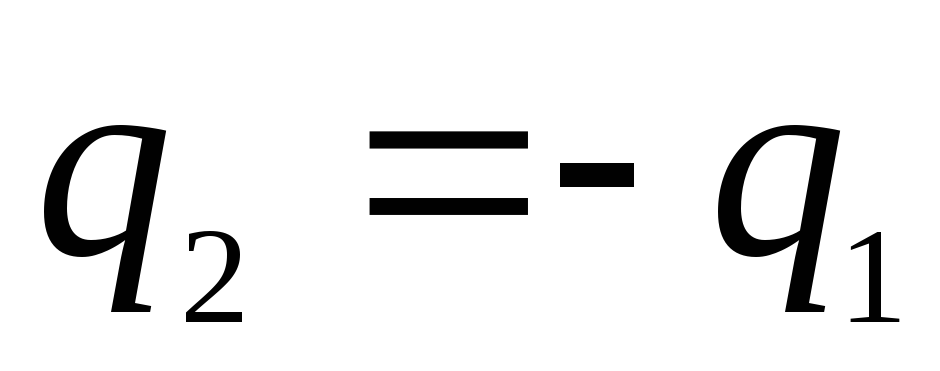 
(tokia sistema vadinama sferiniu kondensatoriumi), tada potencialas išorinėje srityje išnyksta, o tarp plokščių yra
.
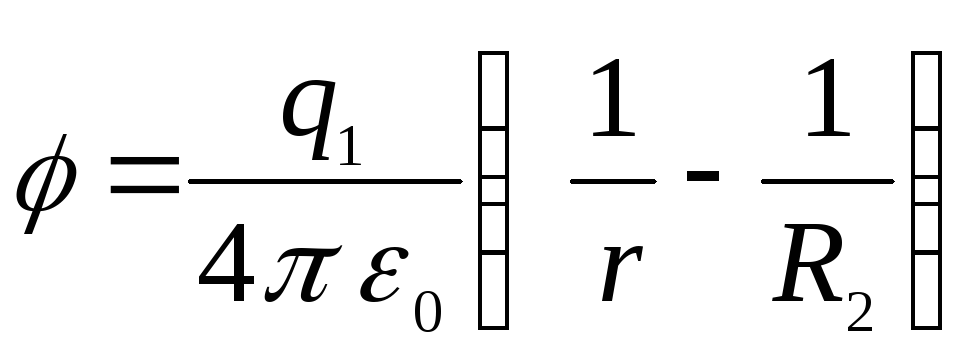Pasirodo grafikas, parodytas ___2 paveiksle.
Jei vidinė sfera turi neigiamą krūvį, o išorinė – teigiamą, tada grafikas yra apverstas ir atrodo kaip ____3 paveiksle.
7.5. Puasono lygties integravimas sferinėmis koordinatėmis. Pristatome sferinę koordinačių sistemą 
,
,, imant rutulio centrą kaip pradžią. Gauso lygtis diferencine forma (Puasono lygtis), kuri nustato lauko potencialą, įgauna formą
kur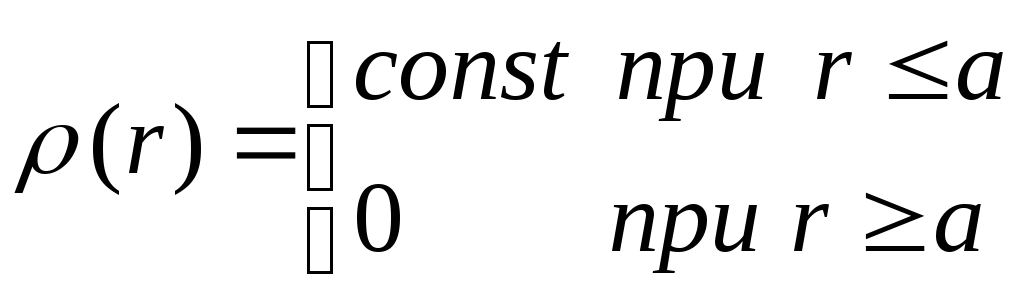 
.
Dėl sferiškai simetriško krūvio pasiskirstymo potencialas priklauso tik nuo atstumo r ir nepriklauso nuo kampų ir , t.y. 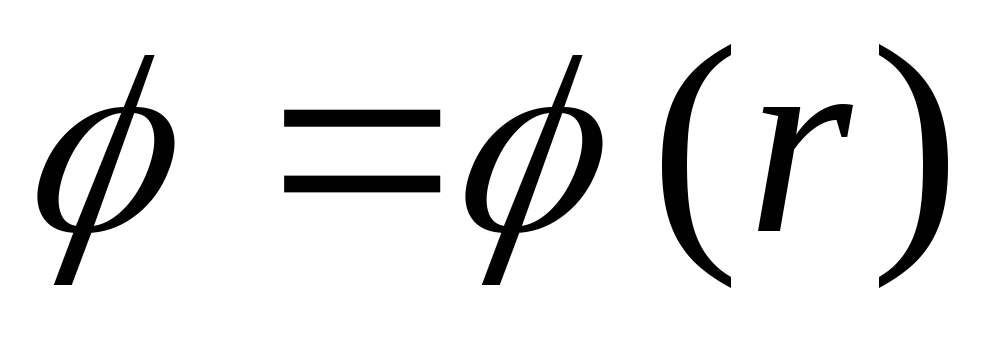. Todėl Puasono lygtis yra supaprastinta ir įgauna formą
.
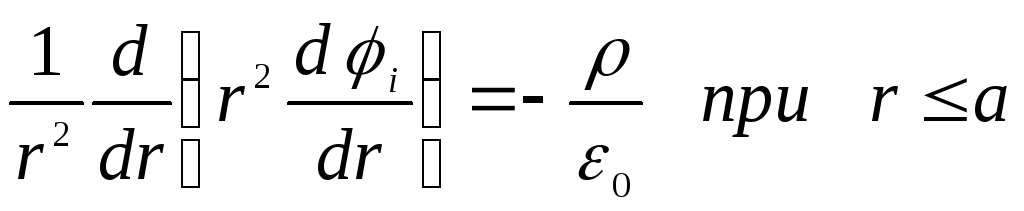
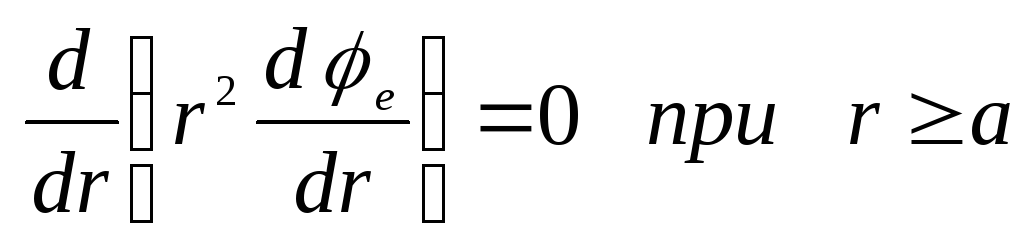Čia per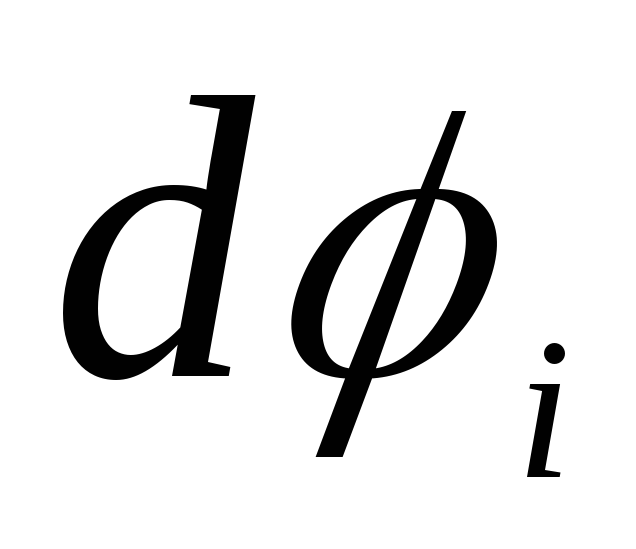 
reiškia potencialą rutulio viduje ir per 
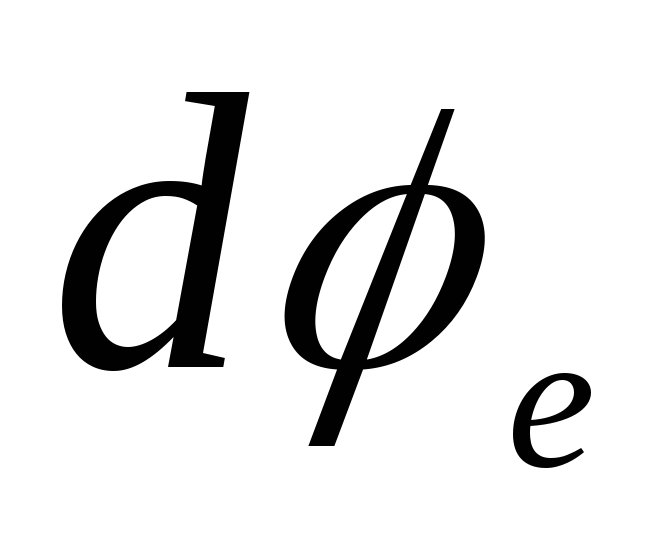- už kamuolio ribų. Integravę šias lygtis, randame
,
.
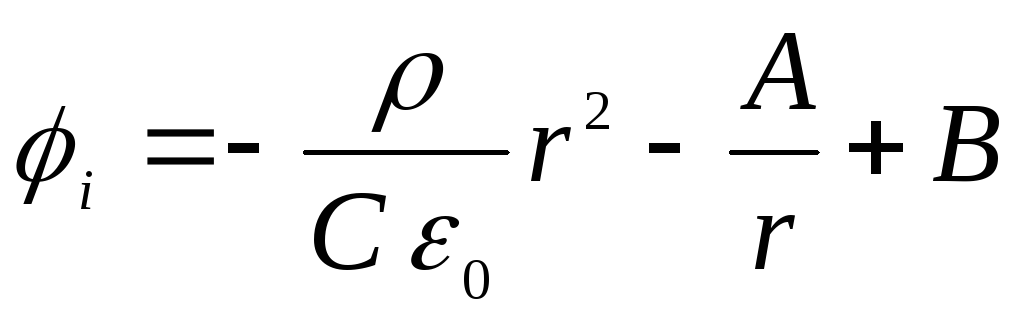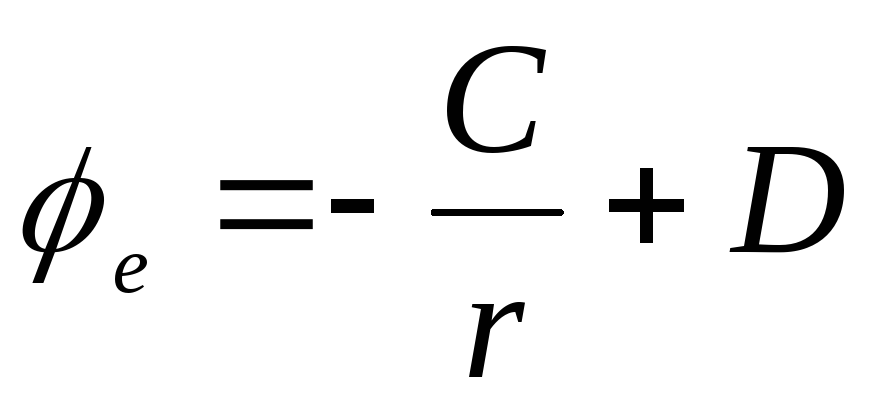Konstantos A, B, C, D turi būti nustatytos pagal šias ribines sąlygas.
1) Potencialas 
turi išlikti baigtinis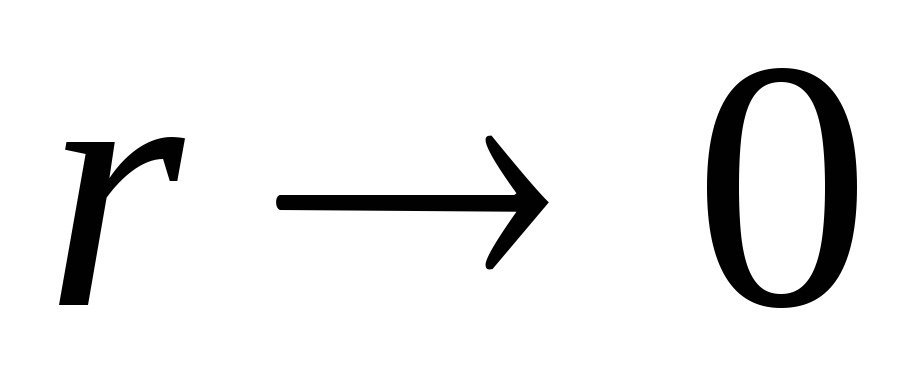 
, o tai tiesiogiai reiškia 
.
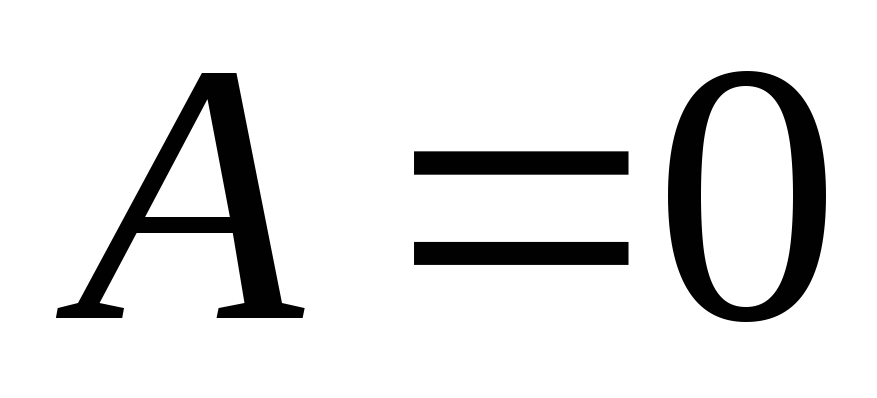2)
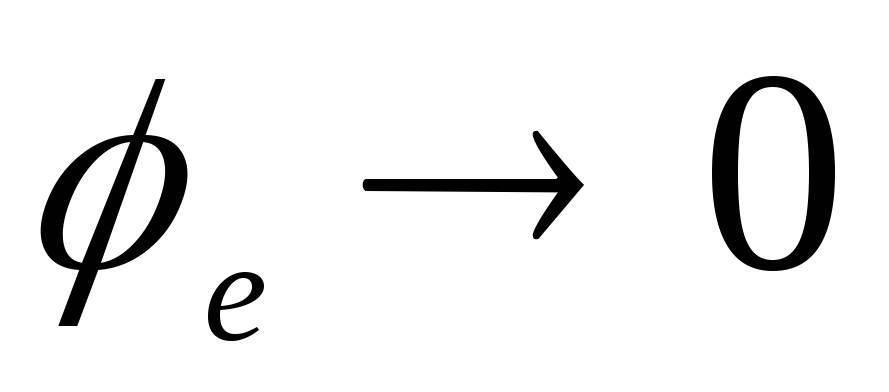adresu 
, iš kur tai išplaukia 
.
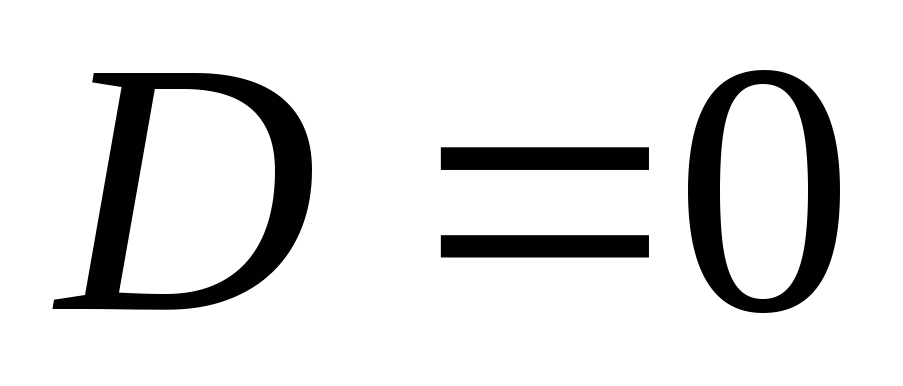3) Elektrostatinio lauko potencialas yra nuolatinė koordinačių funkcija, todėl būtina, kad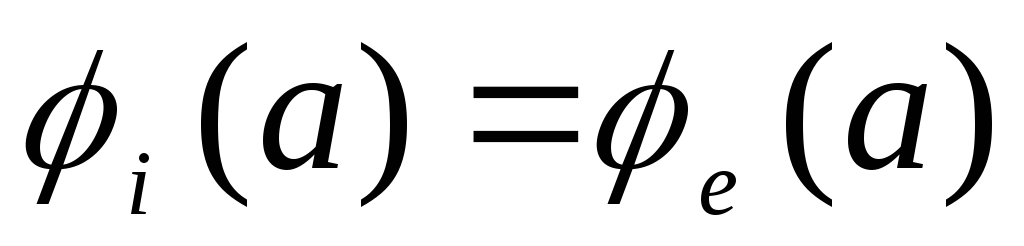 
.
4) Normalioji vektoriaus dedamoji neturėtų patirti šuolio perduodant kamuoliuko paviršių, t.y.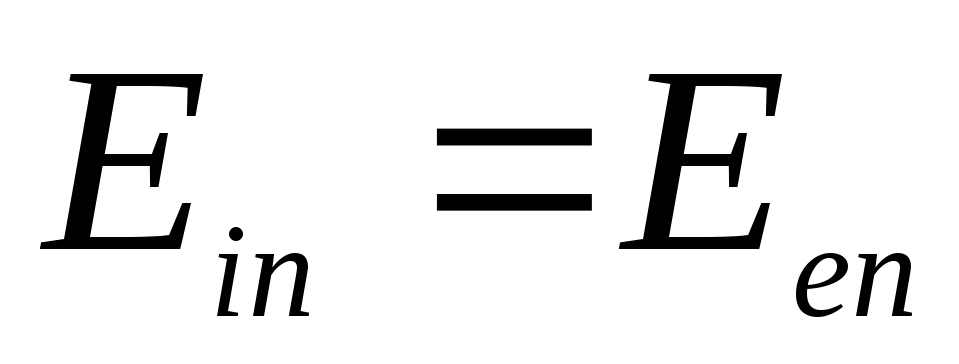 
adresu 
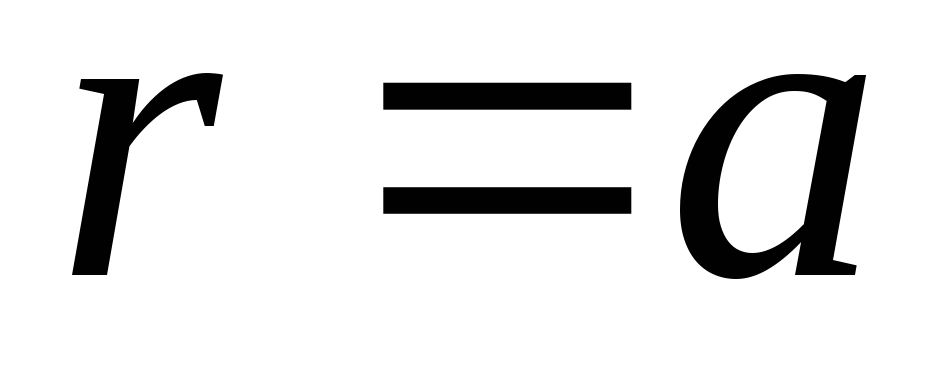, nes paviršiaus krūvio tankis rutulio paviršiuje yra lygus nuliui. Paskutinė sąlyga yra lygiavertė reikalavimui
.
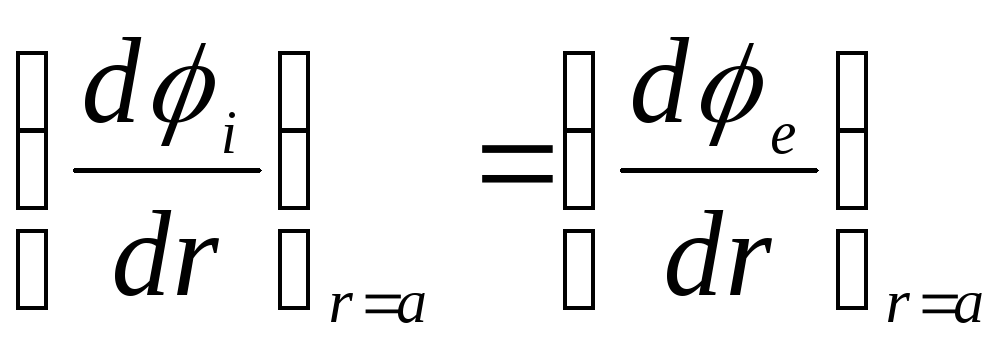Iš paskutinių dviejų sąlygų randame
,
.
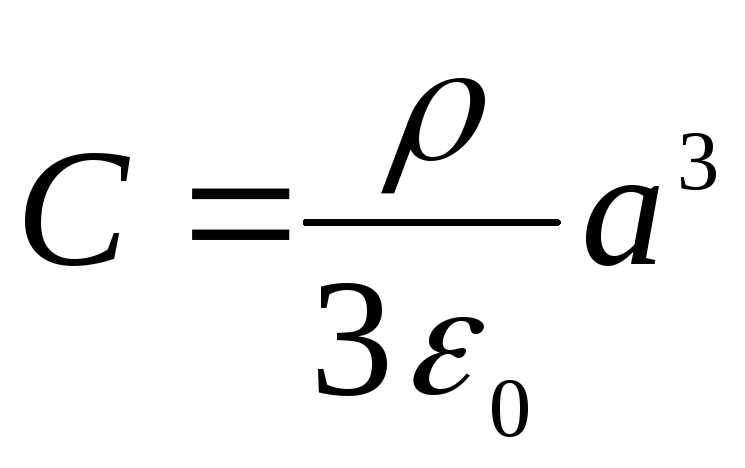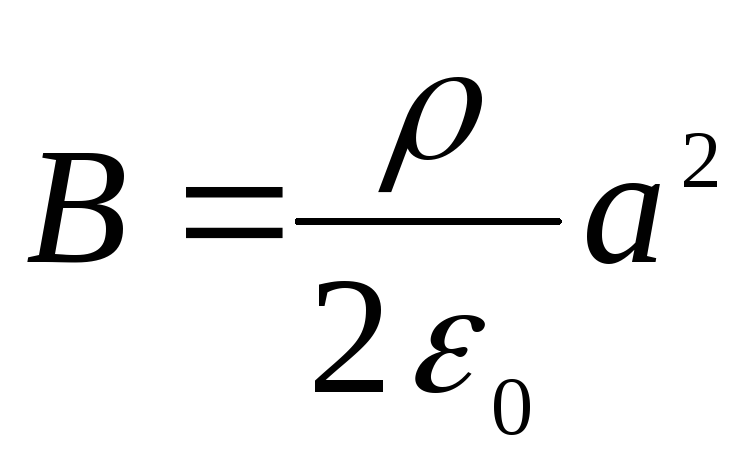Galiausiai formoje įrašome norimus potencialus
,
.
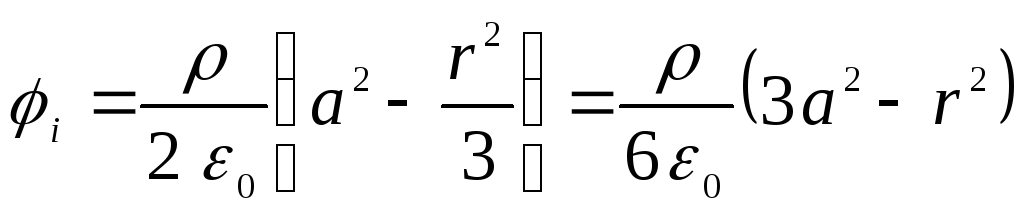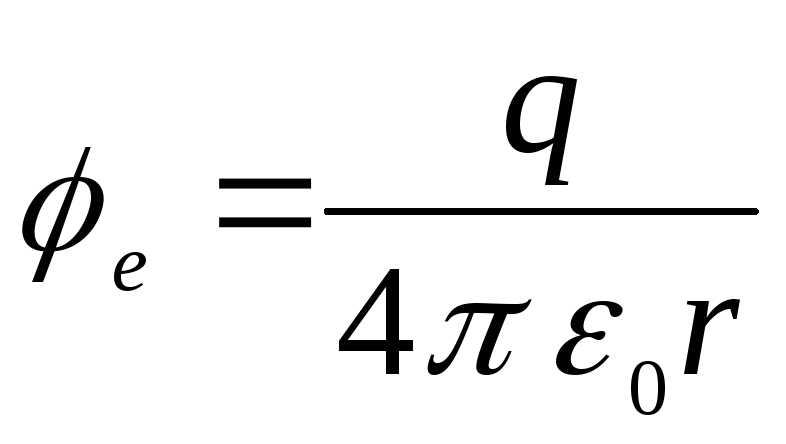Iš šių formulių matyti, kad už rutulio ribų lauko potencialas yra panašus į taškinio krūvio lauką.
Nubraižykime grafiką .
Leisti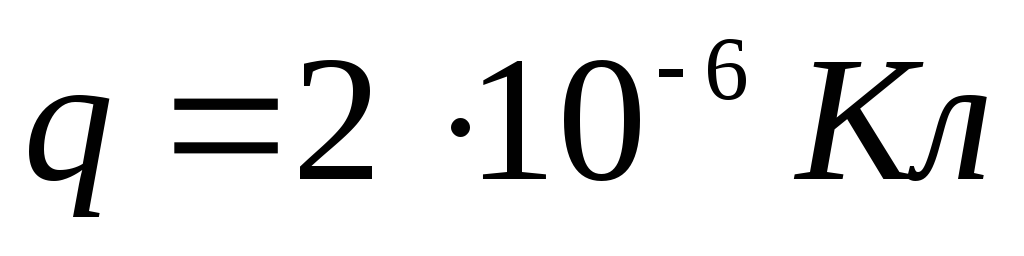 
,
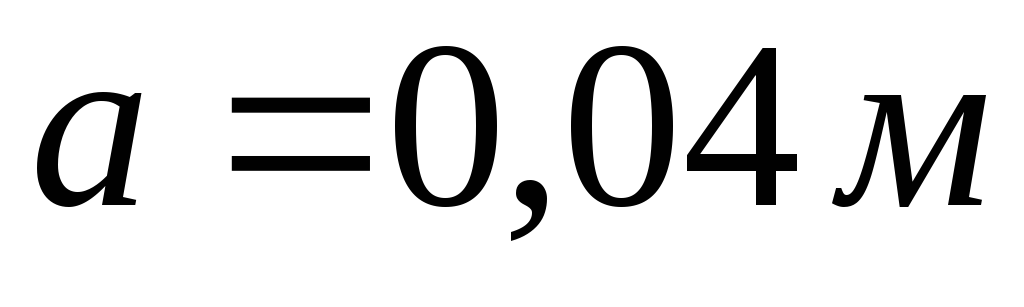. Raskime tūrio krūvio tankį
ir požiūris
.
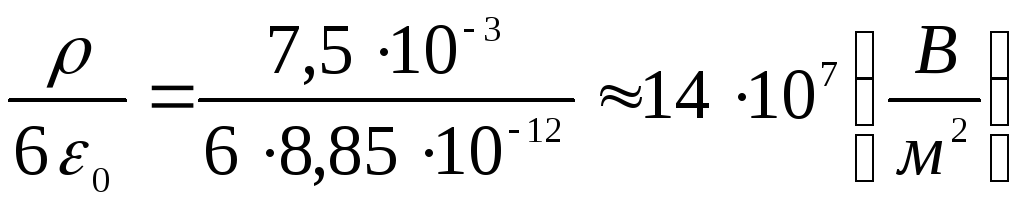Dabar galime parašyti, kad potencialas yra sferos viduje
Padarykime lentelę
|
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Potencialas už taikymo srities ribų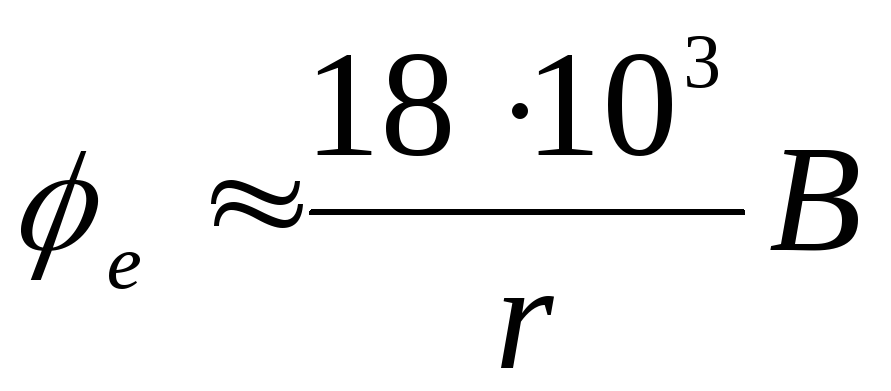 
.
|
| |||||||
|
|
|
|
|
|
|
|
|
Dabar sudarome grafiką .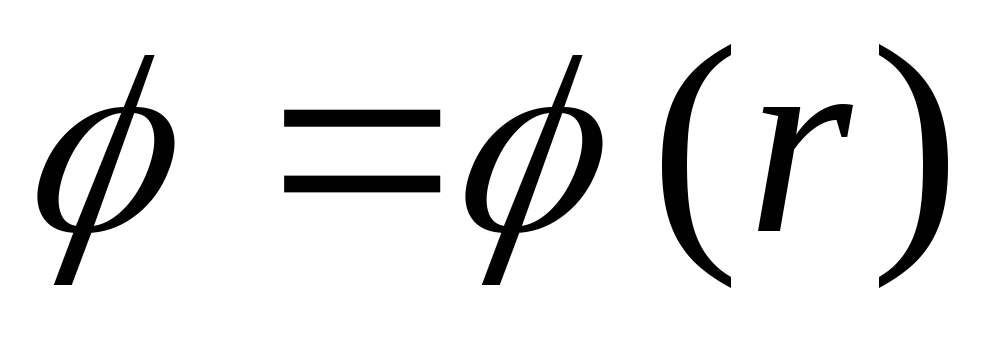
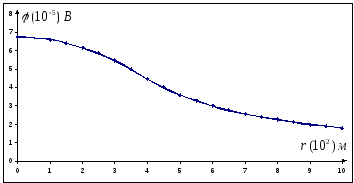
Ryšys tarp įtampos ir potencialo.
Elektrostatinio lauko stiprumo priklausomybė nuo atstumo iki rutulio viduje esančio rutulio centro turi formą (žr. 1.5.4 uždavinio sprendimą).
,
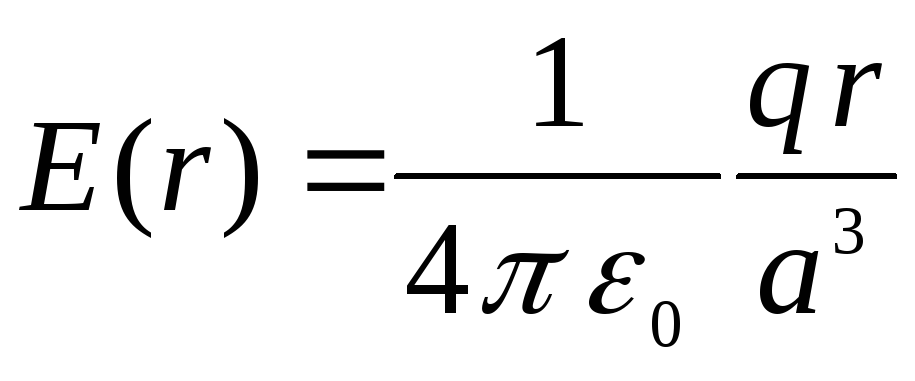tie. sferos viduje lauko stiprumas didėja tiesiškai didėjant atstumui nuo centro. At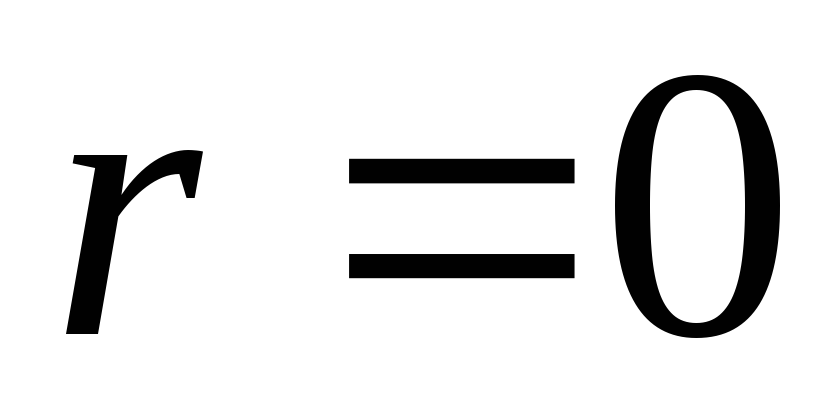 
,
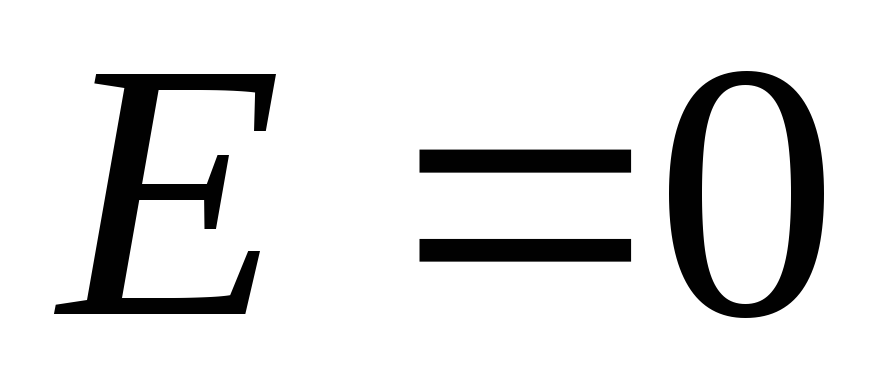, adresu 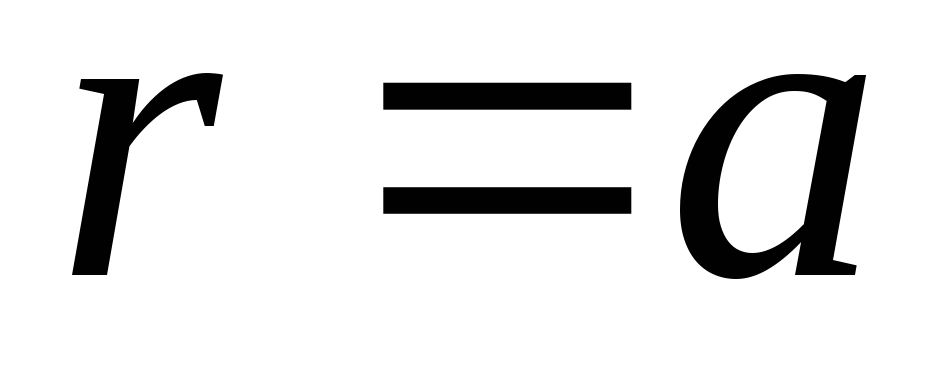jis pasiekia maksimumą ir tampa lygus
.
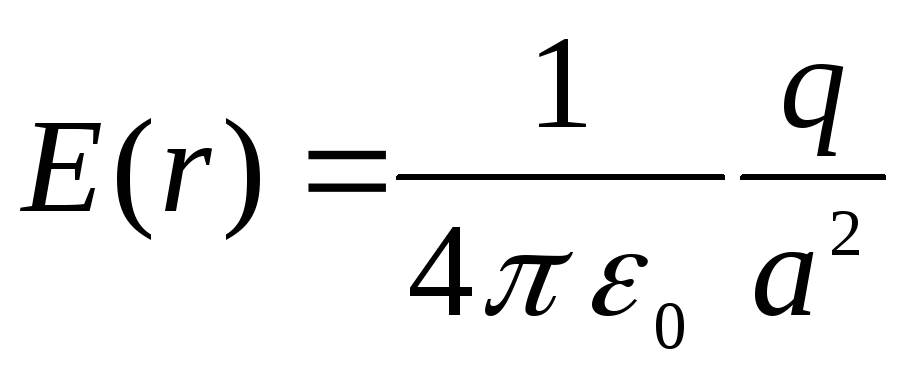At 
lauko stiprumas priklauso nuo atstumo kaip taškinio krūvio lauko stiprumo.
Galimas pokytis įkrauto kamuolio lauke
Lauko potencialas kamuolio viduje
,
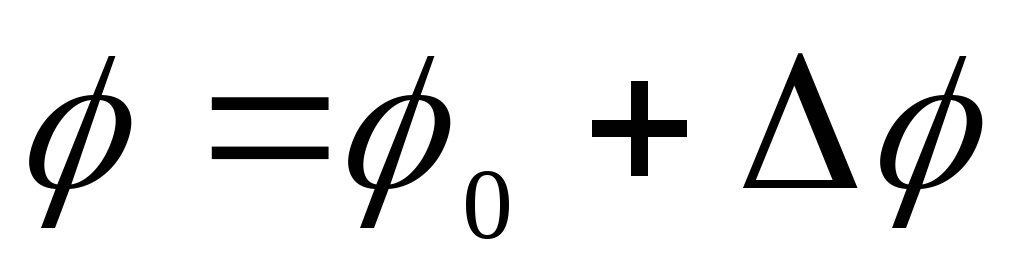kur 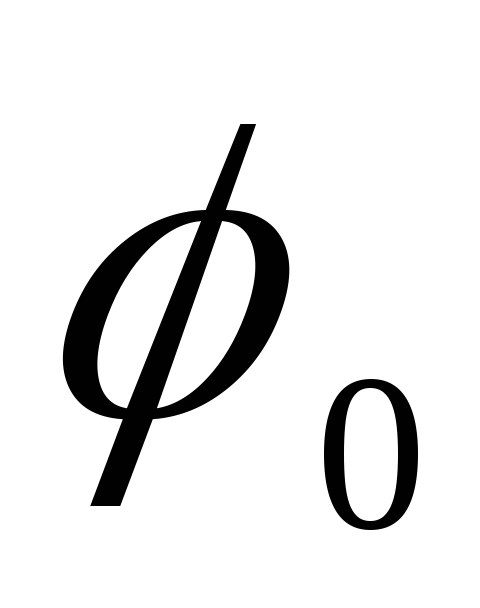yra rutulio paviršiaus taško potencialas (taškinio krūvio lauko potencialas), lygus
.
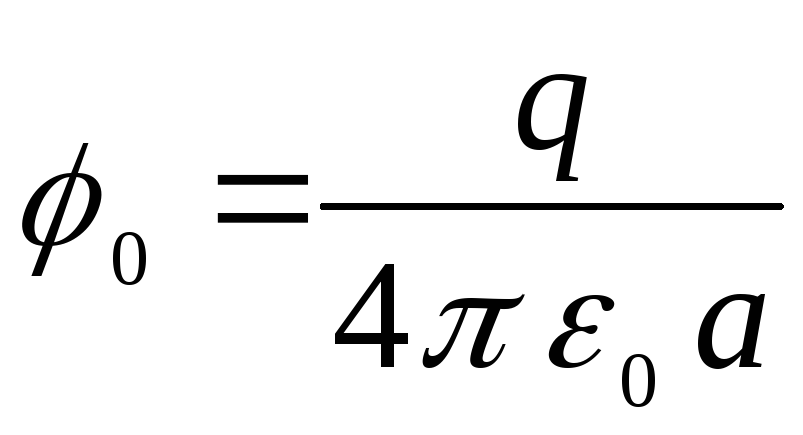Pagaliau gauname
.
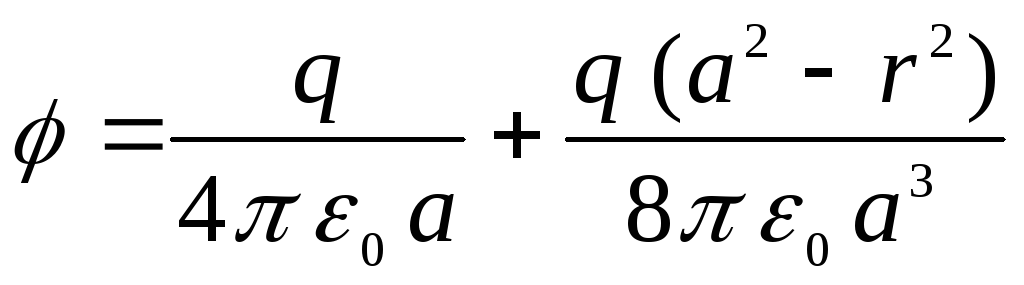Atsižvelgiant į tai, kad tūrinis krūvio tankis
,
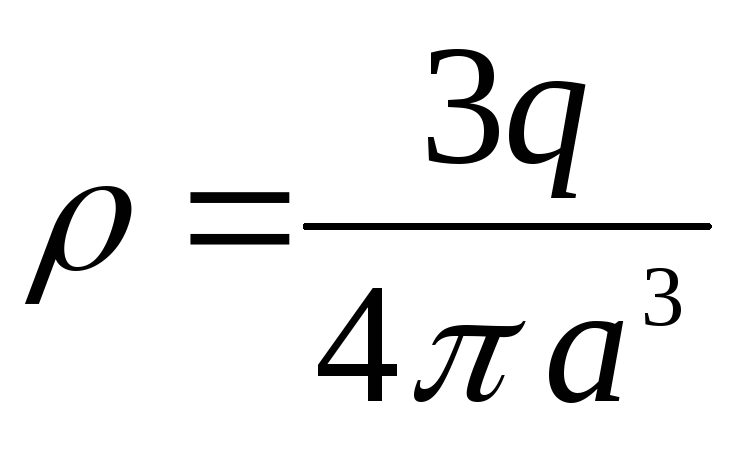galima parašyti
,
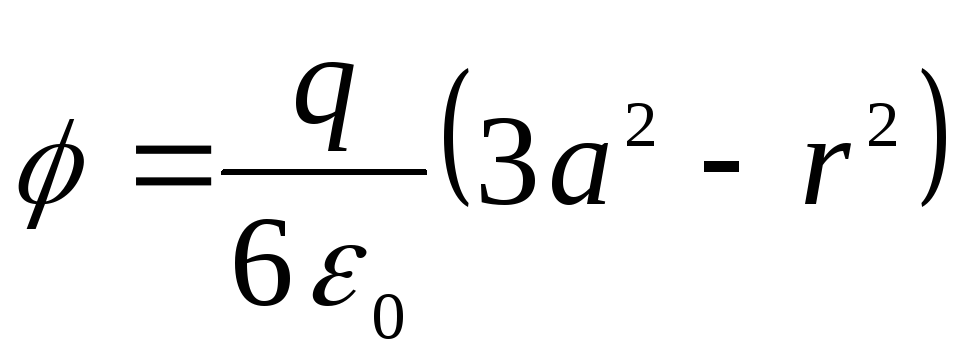tie. priėjome prie tos pačios formulės, kaip ir spręsdami uždavinį integruodami Puasono lygtį.
1.7.6. Gauto lauko potencialas taške A
,
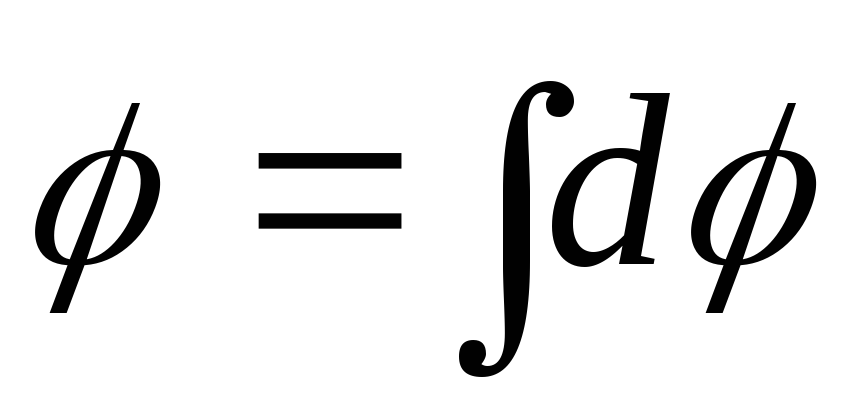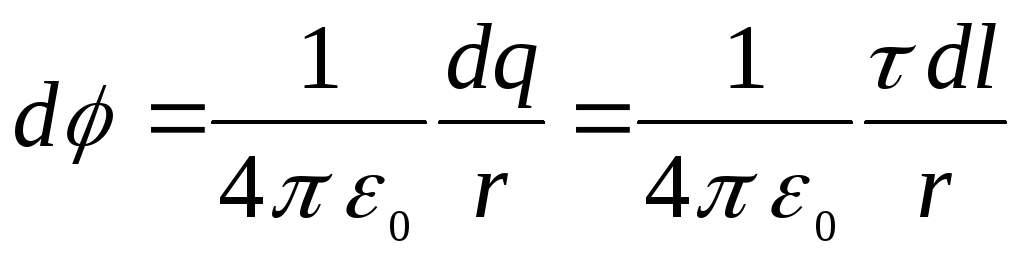
yra krūvio sukuriamo lauko potencialas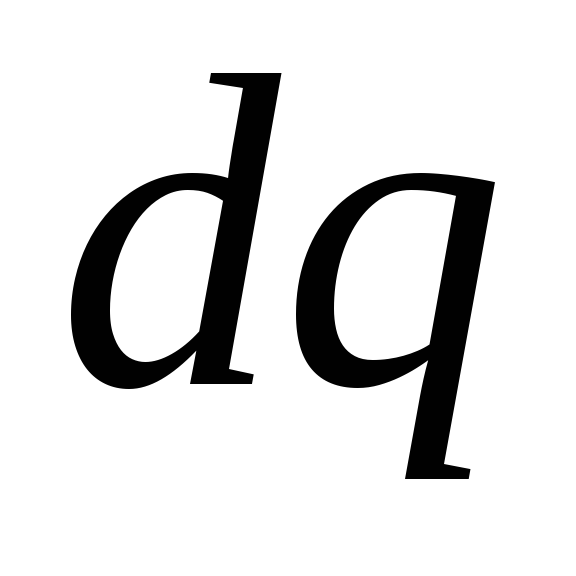 
žiedo elementas 
.
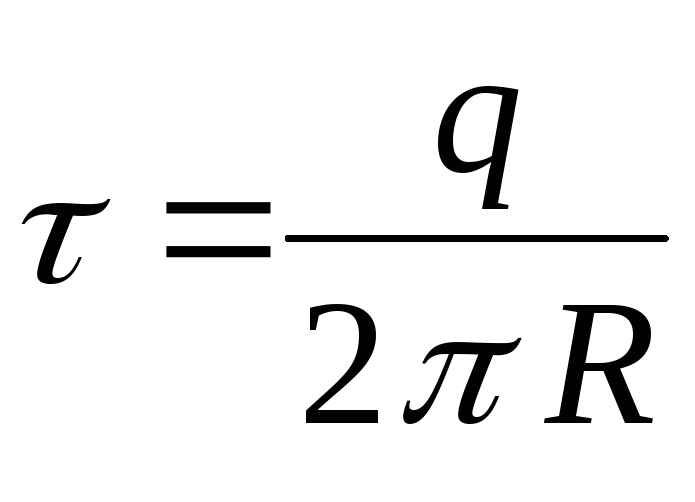
yra tiesinis krūvio tankis, r yra atstumas nuo elemento iki nurodyto taško. Iš paskutinių dviejų formulių turime
.
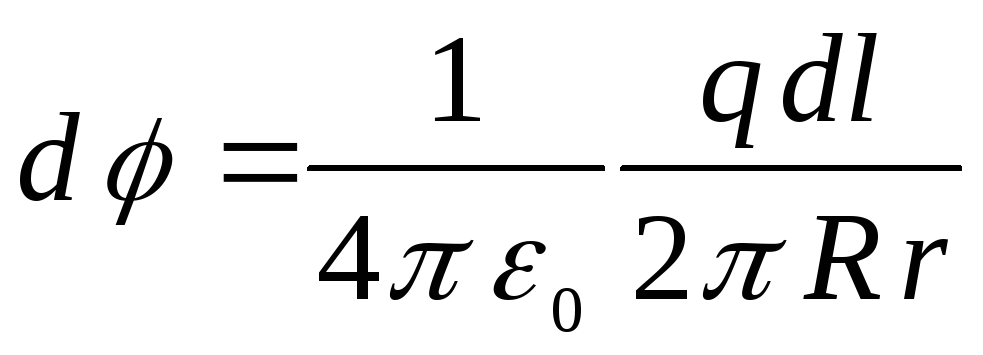Rezultato potencialas
Iš geometrinių svarstymų išplaukia, kad
.
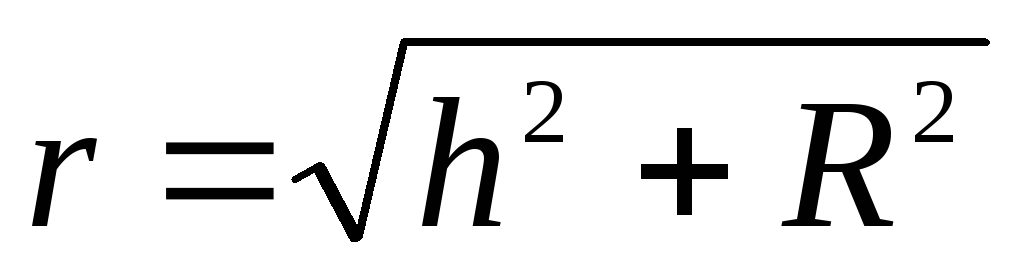Vadinasi,
.
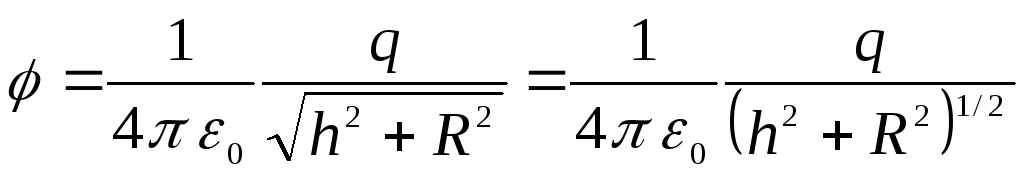Lauko stiprumas
.
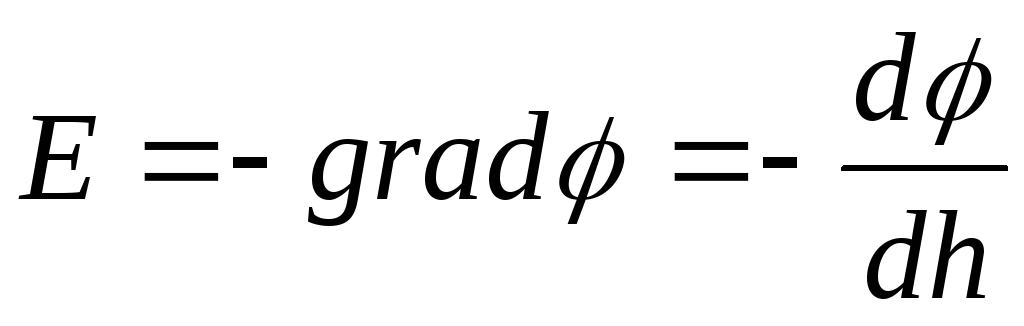Išraiškų analizavimas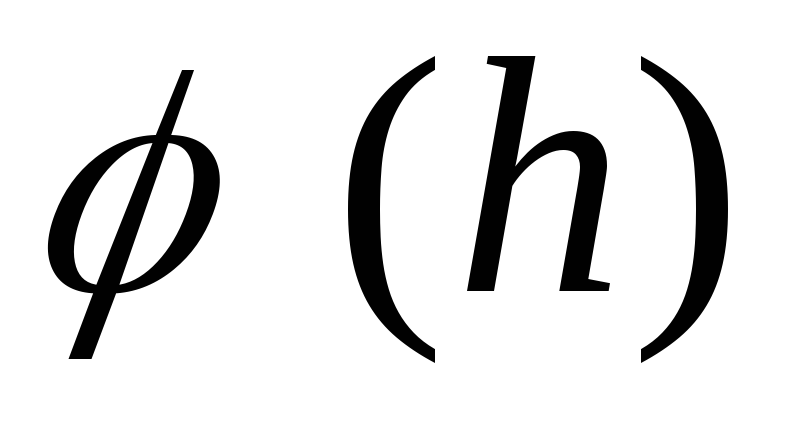 
ir 
rodo, kad žiedo centre (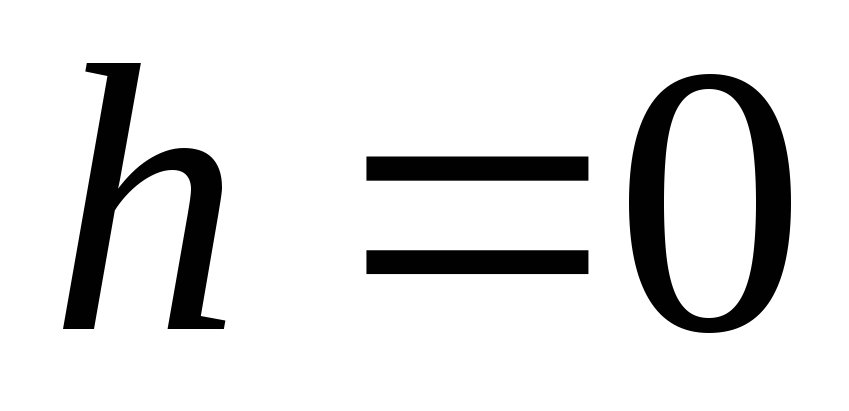 
) potencialas turi didžiausią vertę, o lauko stiprumas išnyksta.
At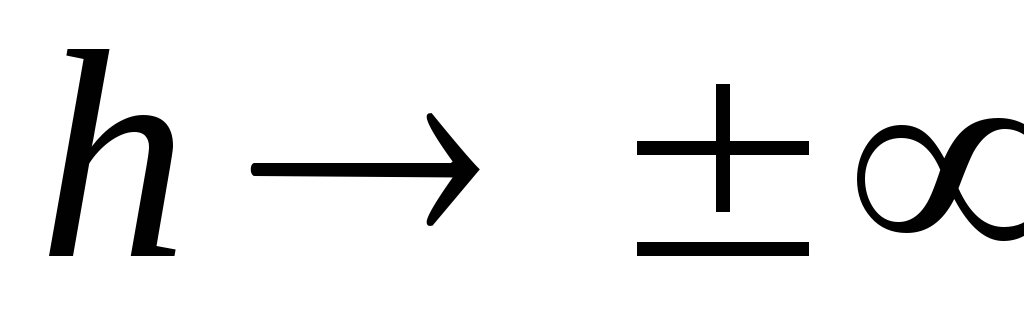 
tiek potencialas, tiek įtampa linkę į nulį.
At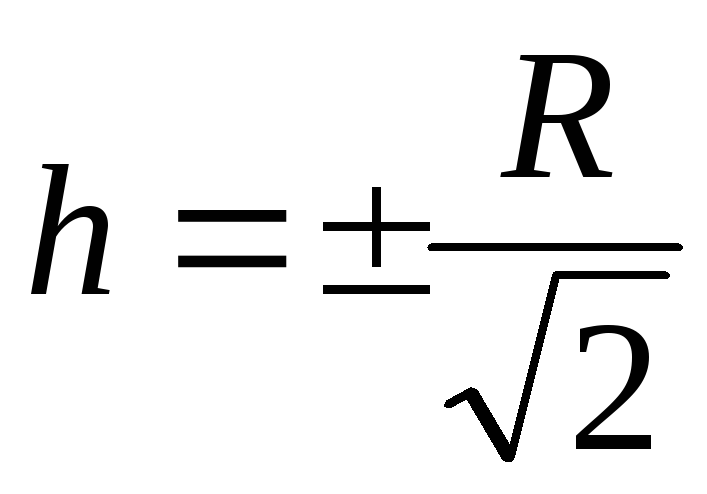 
išvestinė 
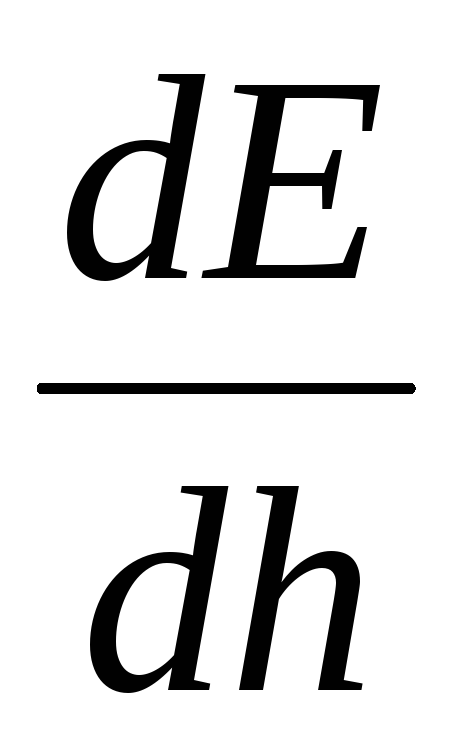išnyksta, todėl šiuo metu lauko stiprumas yra didžiausias ir grafike 
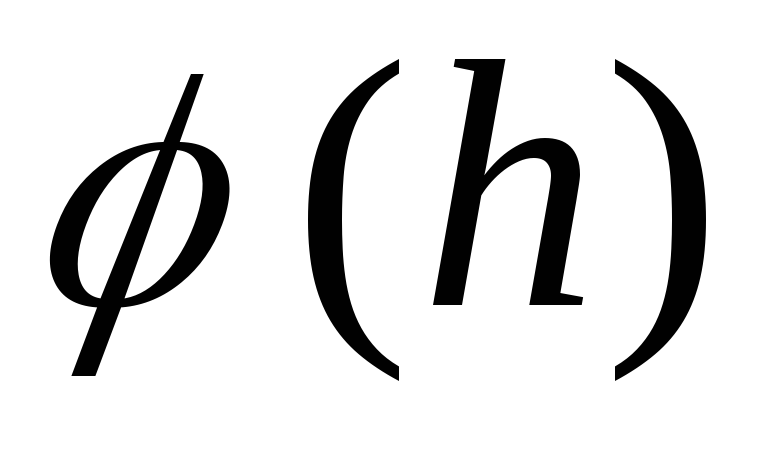(žr. ____ pav.) bus vingio taškas. Tvarkaraštis esančiame I ir III kvartale, t.y.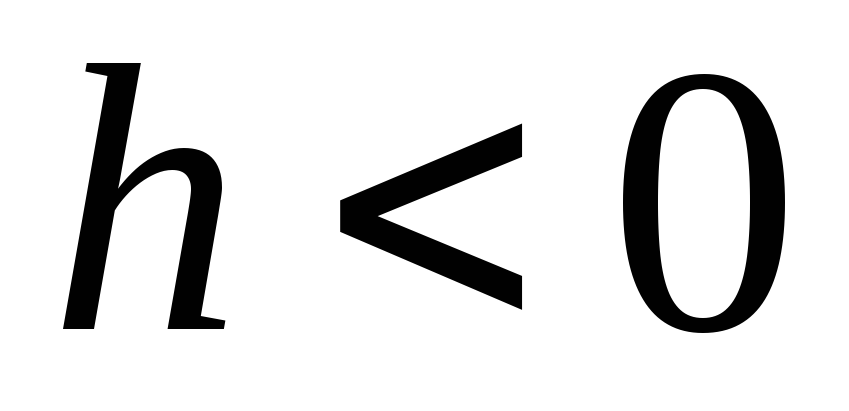 
,
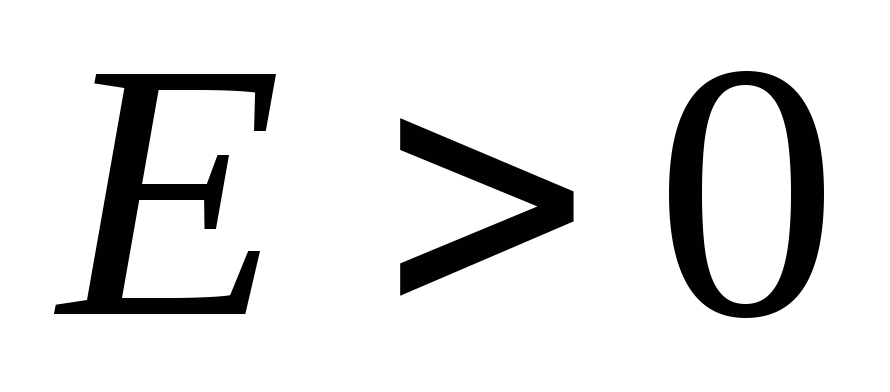. Tai reiškia, kad važiuojant per žiedo centrą ( 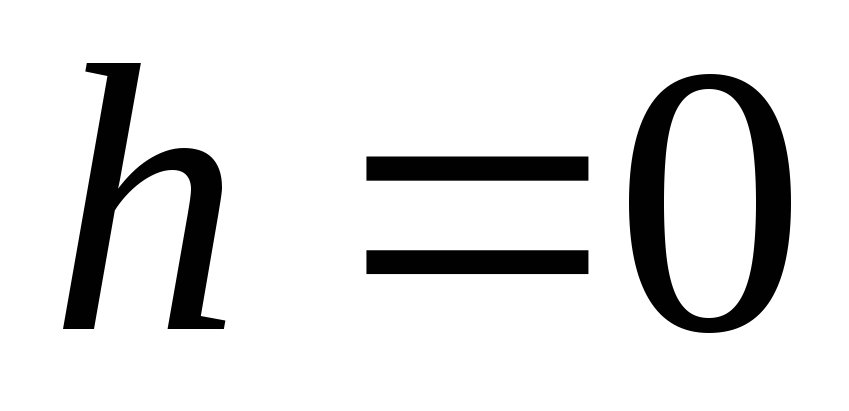) vektorius keičia savo kryptį į priešingą.
Tvarkaraštis 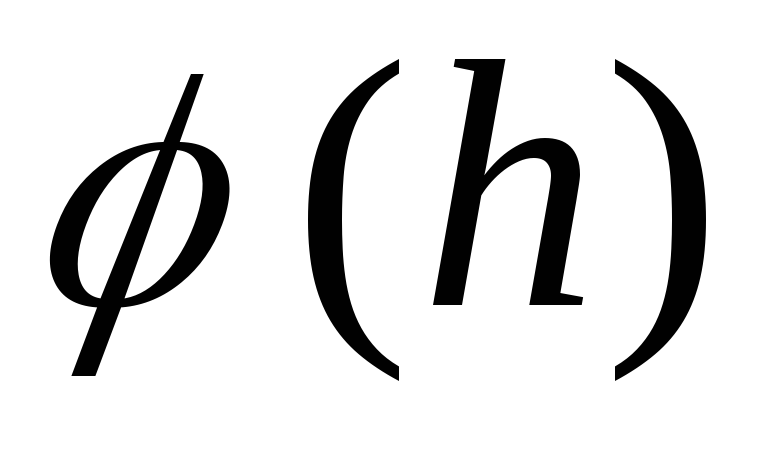esančiame 1 ir 2 kvartale, t.y. abiejose žiedo pusėse taškuose, esančiuose ant jo ašies, potencialas yra teigiamas.
Naudojant šios problemos sprendimo pavyzdį, galima įsitikinti, kad pakeitus potencialo atskaitą, potencialų skirtumas tarp bet kurių dviejų taškų nekinta. Nesikeičia ir visas potencialo priklausomybės nuo atstumo pobūdis. Pavyzdžiui, pasirinkus kilmę žiedo centre, t.y. tariant, kad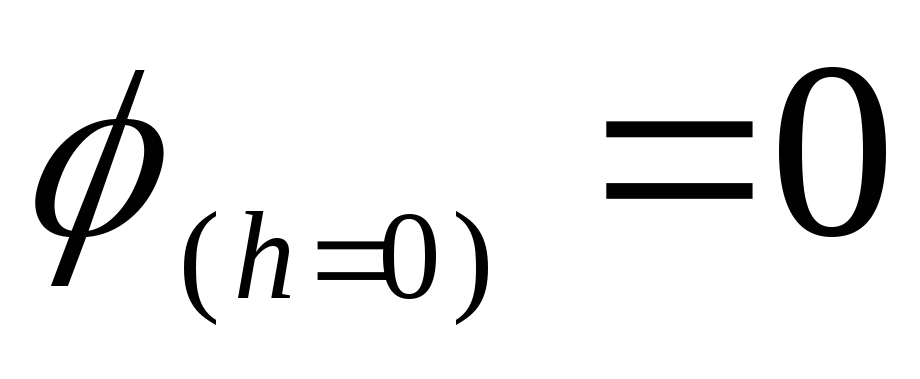 
, tada bet kurio taško, esančio ant žiedo ašies, potencialas yra lygus
.
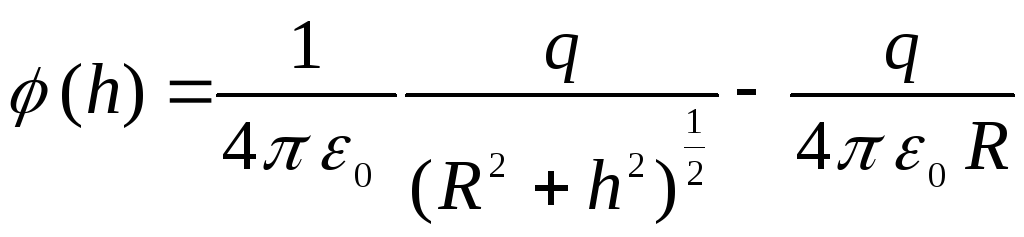Šią formulę galima lengvai gauti remiantis superpozicijos principu.
Jei potencialo pradžia pasirenkama žiedo centre, tai lauko potencialas, kurį sukuria elementarus krūvis 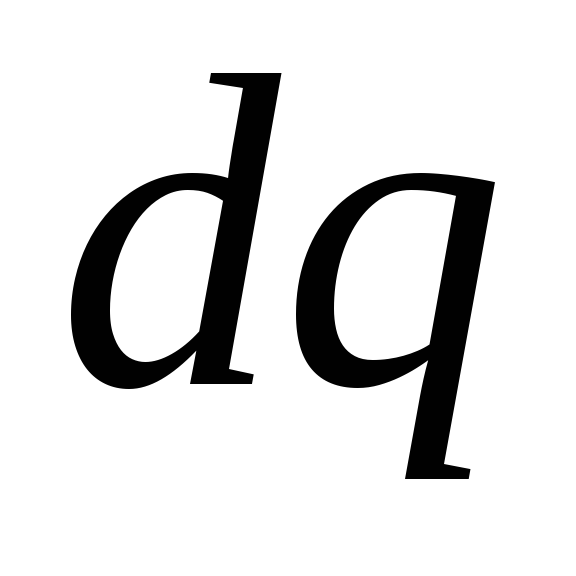taške A, gali būti pavaizduotas kaip
.
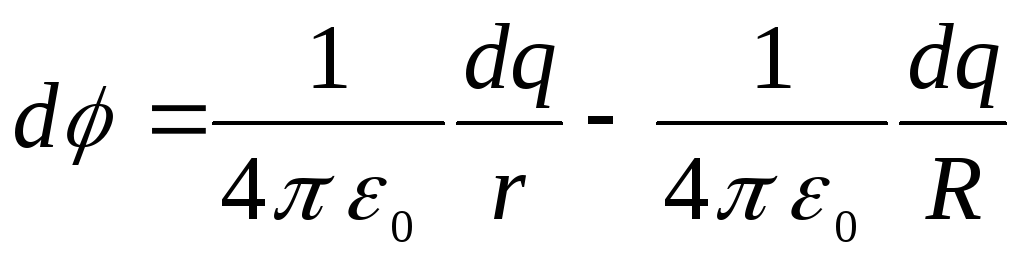Integruodami šią išraišką visame žiede, gauname formulę
.
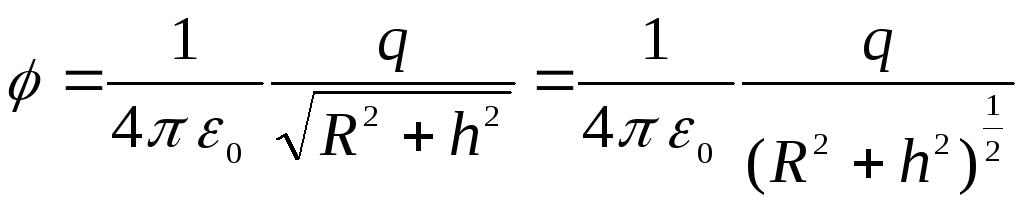priklausomybės grafikas 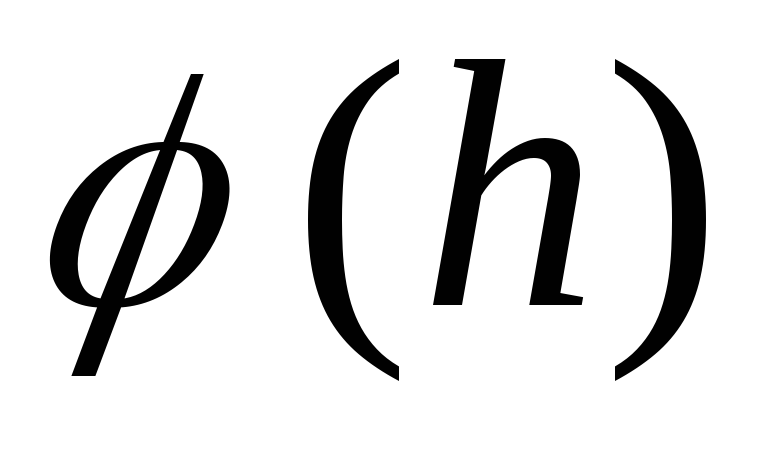, nekeisdamas savo charakterio, tam tikru dydžiu pasislenka lygiagrečiai sau 
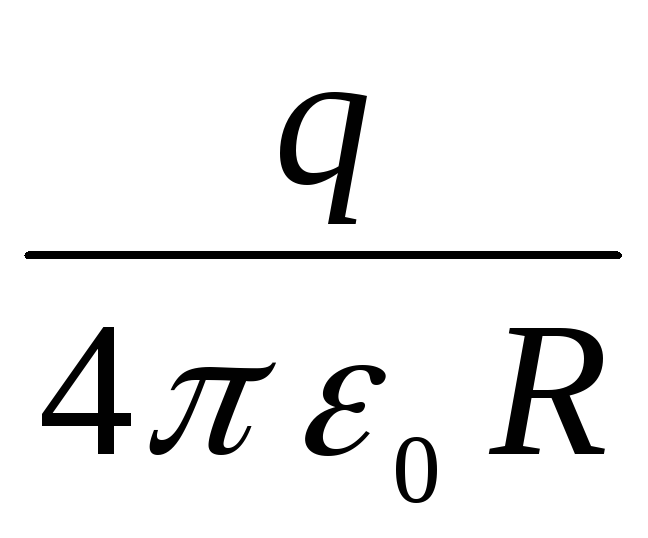(punktyrinė linija _____2 paveiksle). At 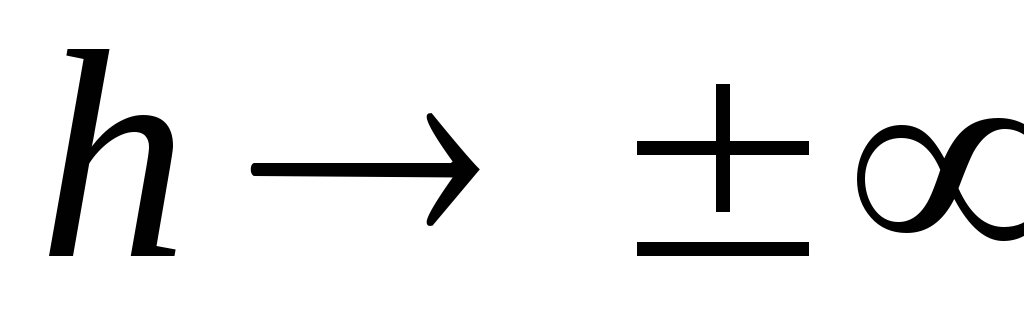potencialas linkęs vertinti 
.
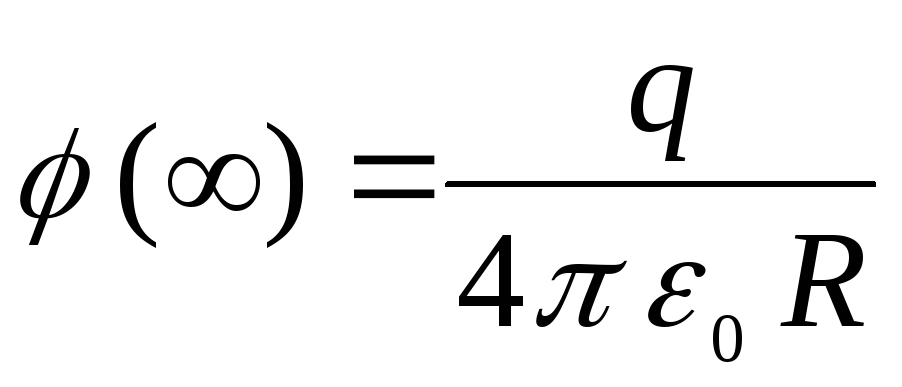7.7. Potencialas skaitiniu požiūriu prilygsta darbui, atliekama elektrinio lauko jėgų perkeliant vienetinį teigiamą krūvį iš tam tikro lauko taško (mūsų atveju – nuo vidinės sferos paviršiaus) į begalybę, t.y.
,
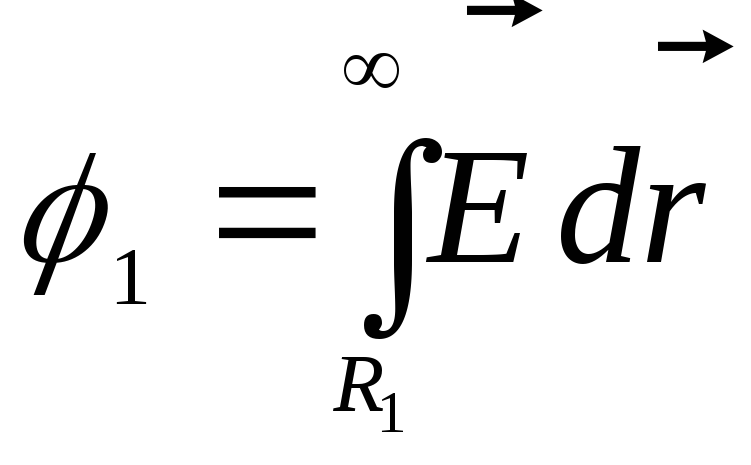kur yra gautas lauko stiprumas visuose integravimo intervalo taškuose.
Intervale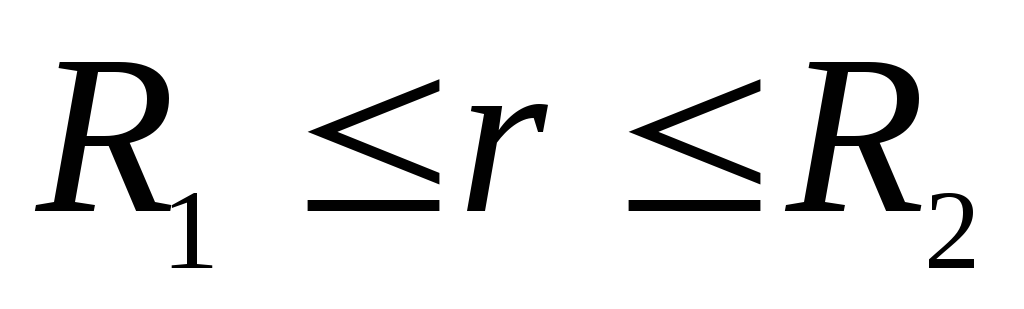 
lauką sukuria tik vidinės sferos krūvis. Vektorius , nepriklausomai nuo krūvio dydžio ir ženklo , nukreiptas išilgai spindulio nuo centro. Perkeliant vienetinį teigiamą krūvį iš prieš lauko pajėgos atlieka teigiamą darbą. At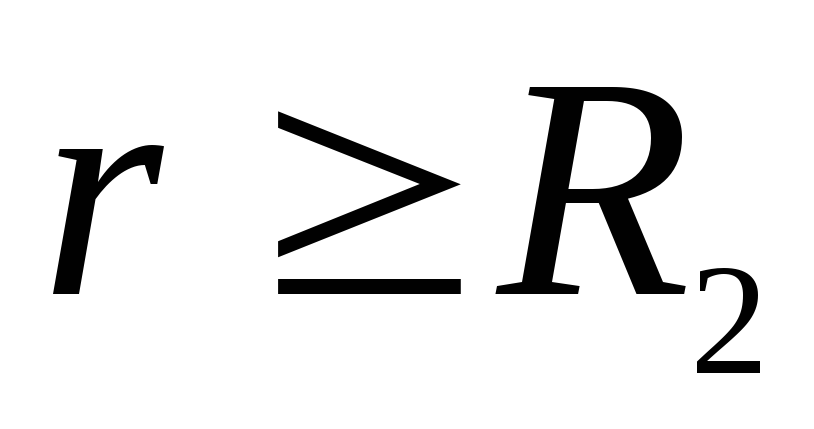 
, t.y. už antrosios sferos lauko jėgų darbas yra neigiamas, taigi ir vektorius nukreiptas išilgai spindulio link sferos centro. Taškuose 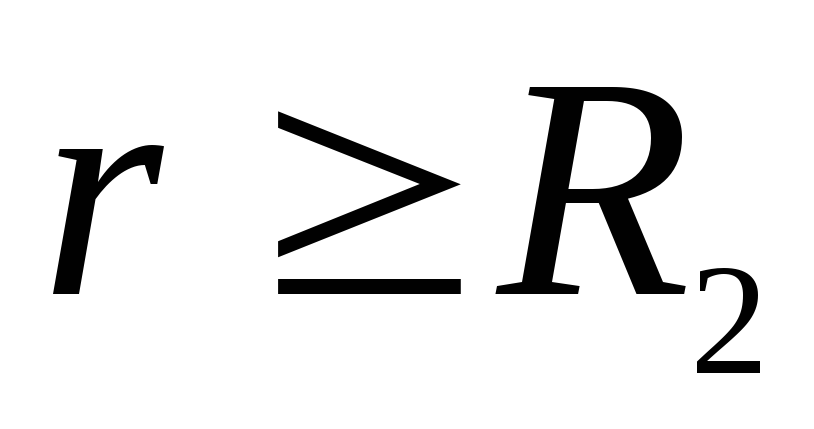laukas nustatomas pagal abiejų sferų krūvių algebrinę sumą. Įkrauti 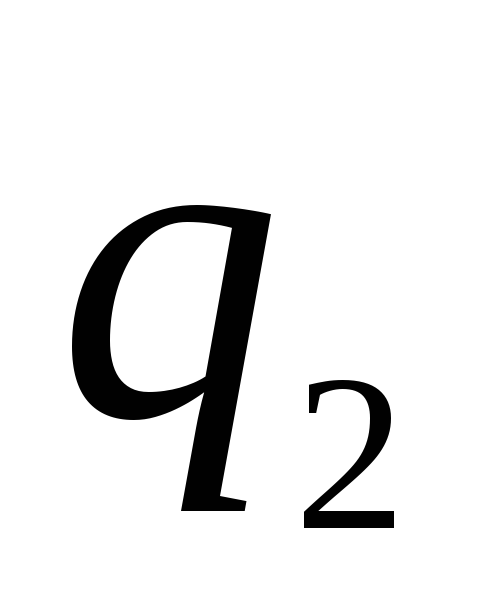turi būti neigiamas ir turi būti didesnis už krūvį 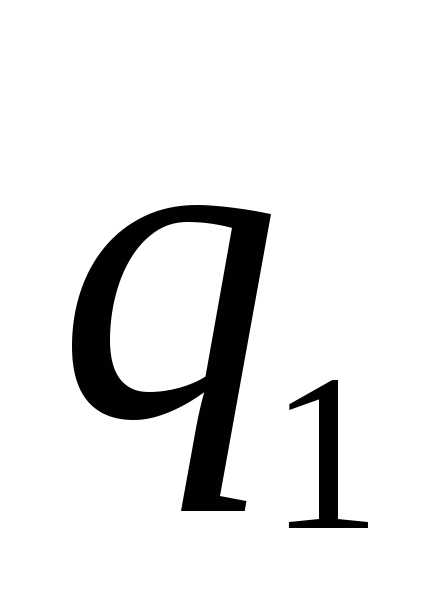. Kadangi vektoriai ir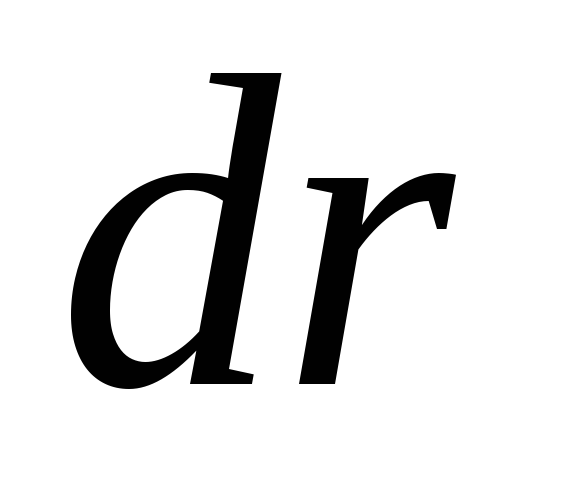 
kolinearinis (arba antikolinearinis, jei 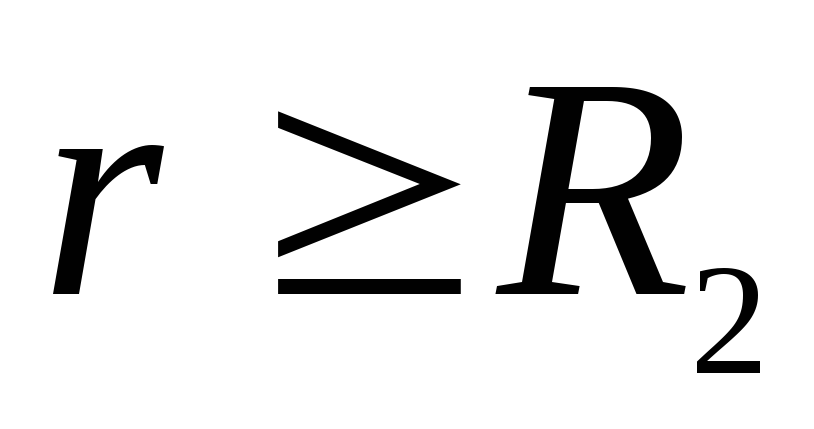), tada skaliarinė sandauga 
gali būti pakeistas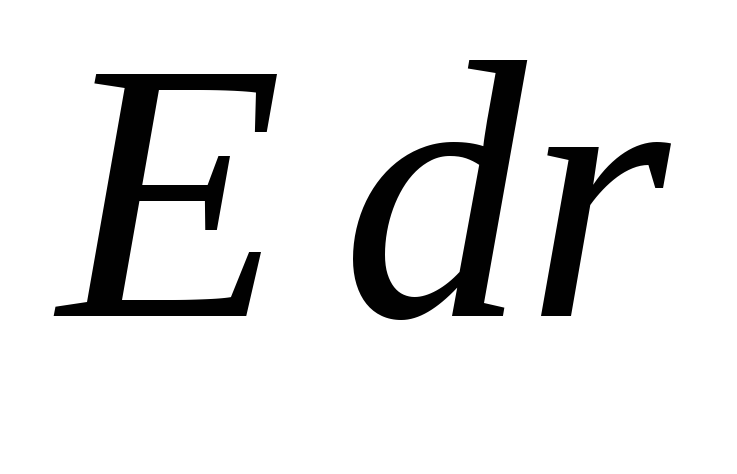 
(tuo atveju, kai šie du vektoriai nukreipti priešingai, lauko stiprumas turėtų būti laikomas neigiamu). Formulėje 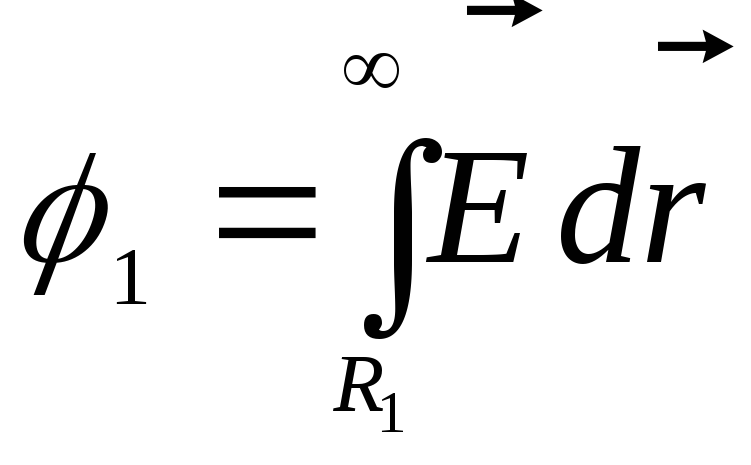integrandas 
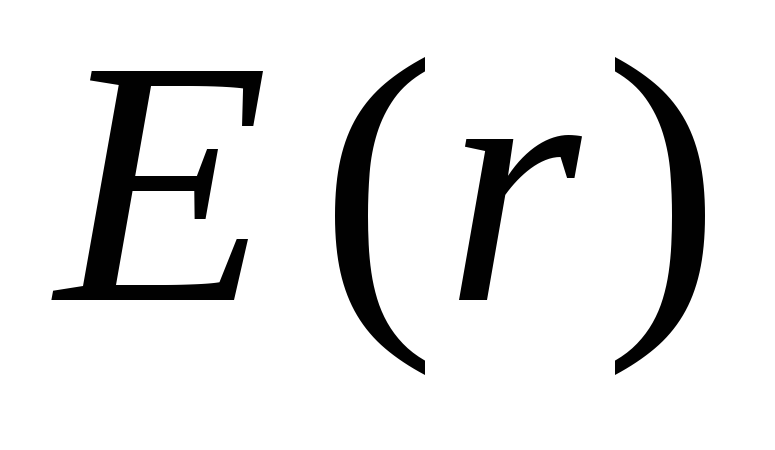nutrūksta taške 
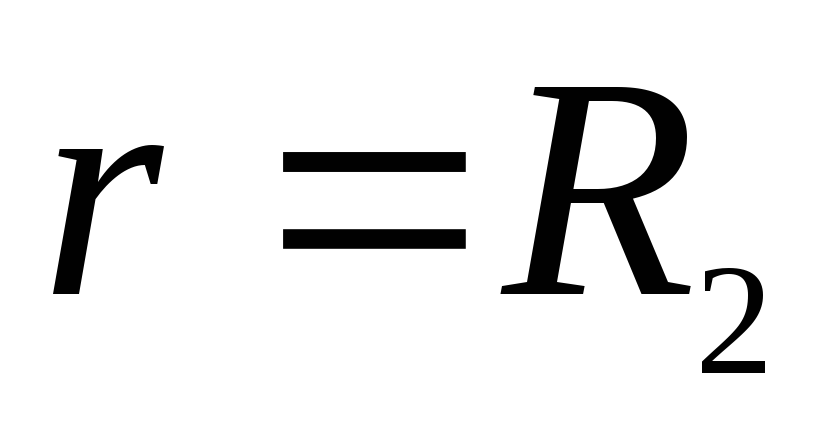. Todėl integralas turi būti padalintas į du integralus nuo prie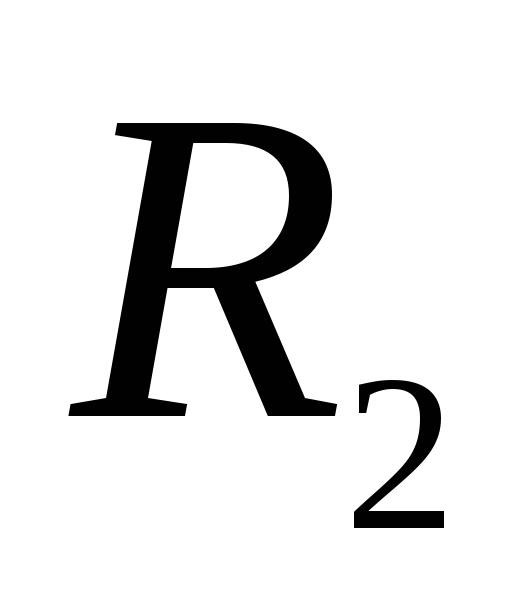š ir i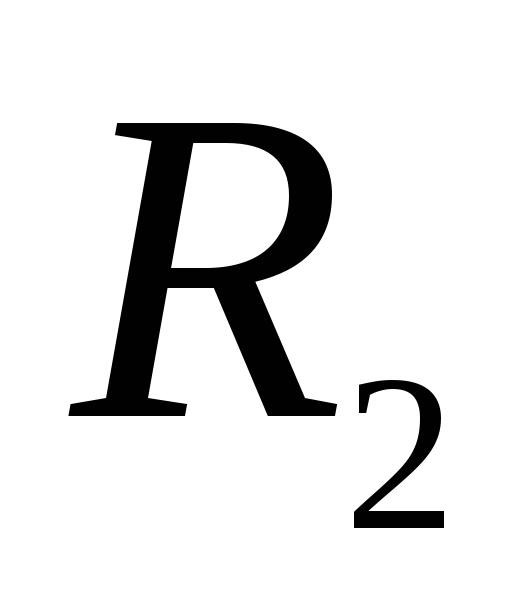š prieš 
:
.
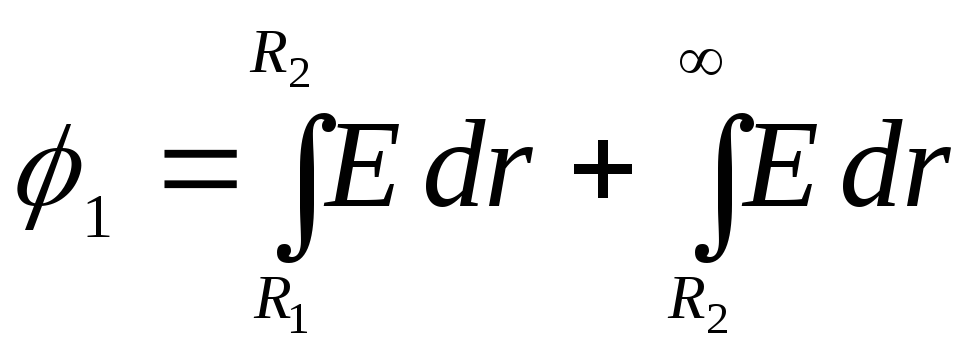At 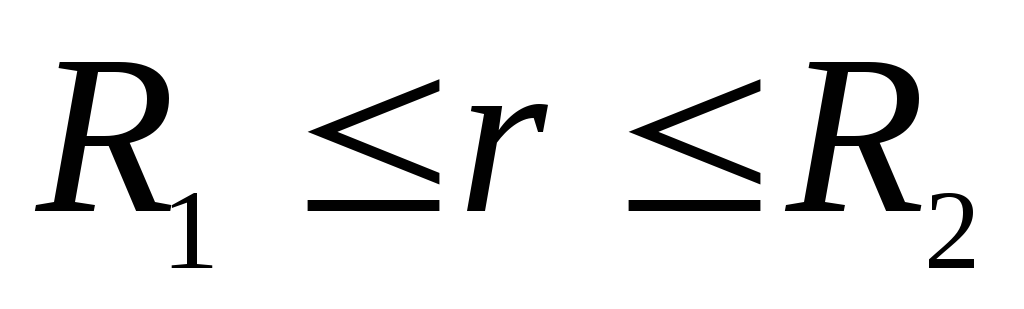įtampa
,
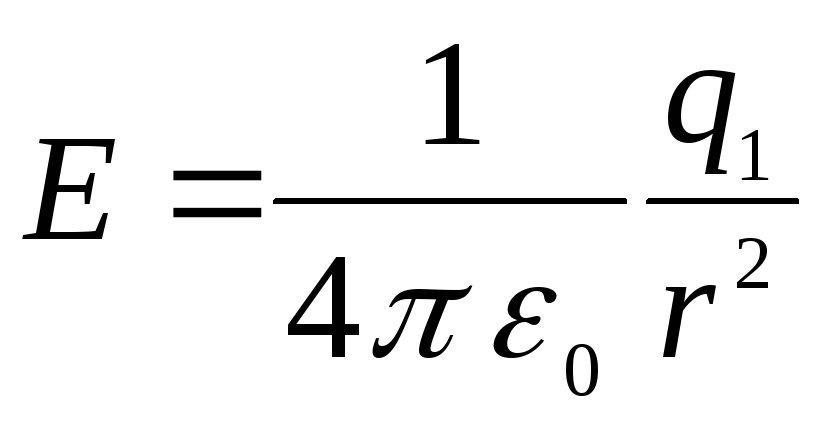ir pas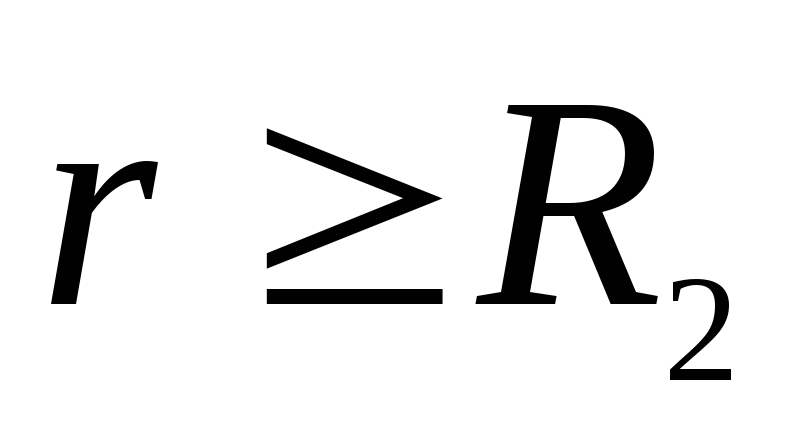 
.
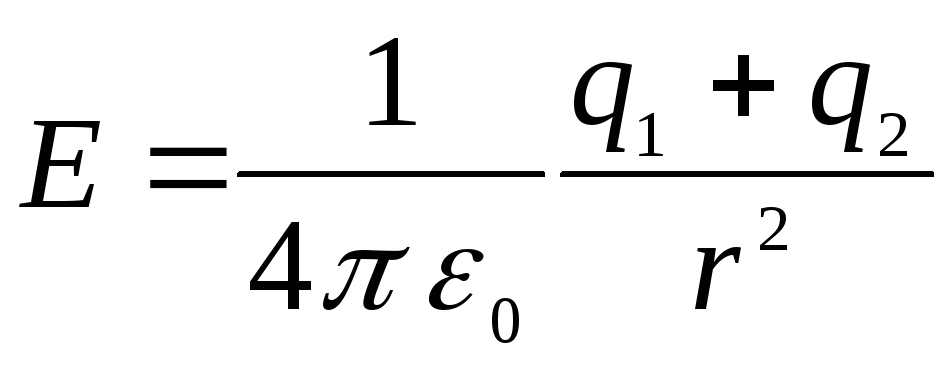Pakeitę šias išraiškas į atitinkamus integralus, gauname
.
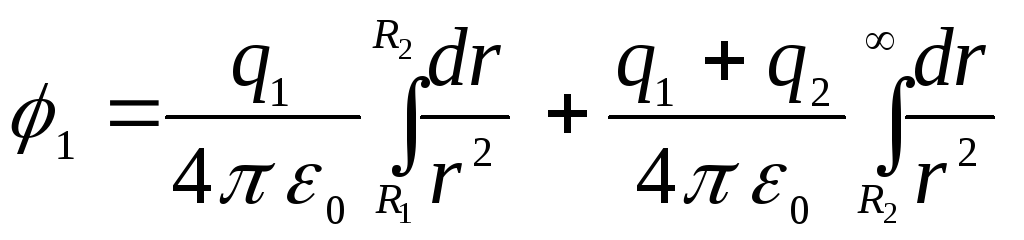Integruodami ir sumažindami panašius terminus gauname
.
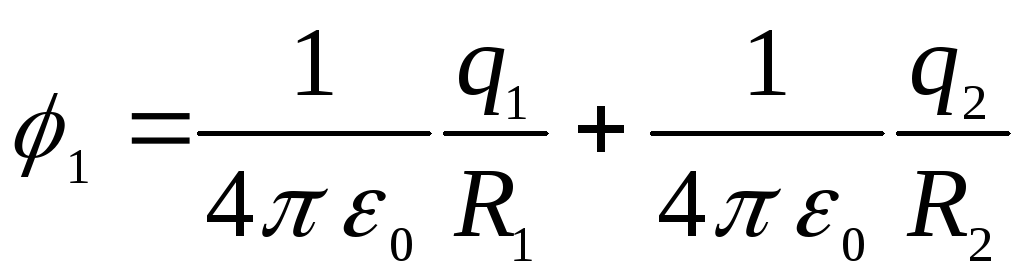Kadangi pagal problemos būklę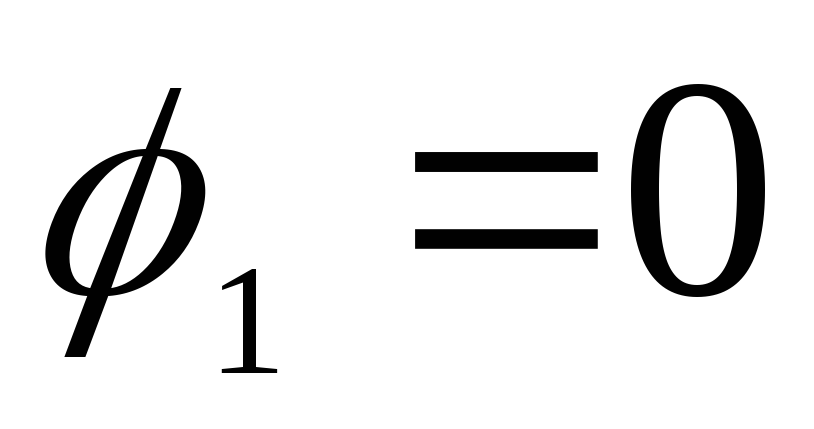 
, tada
.
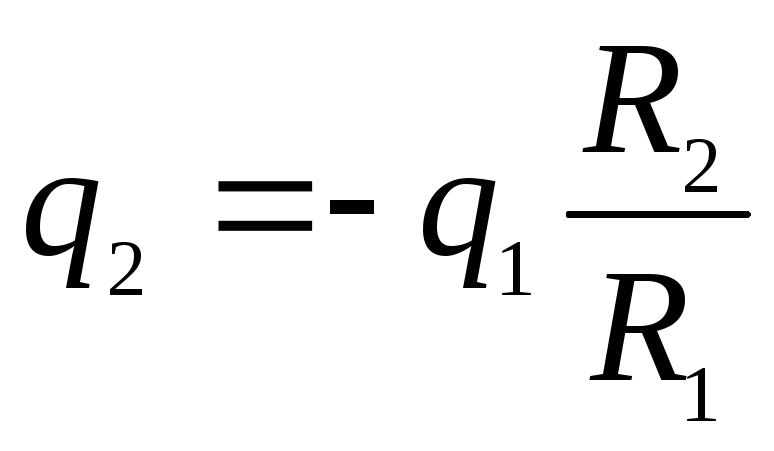priklausomybės grafikas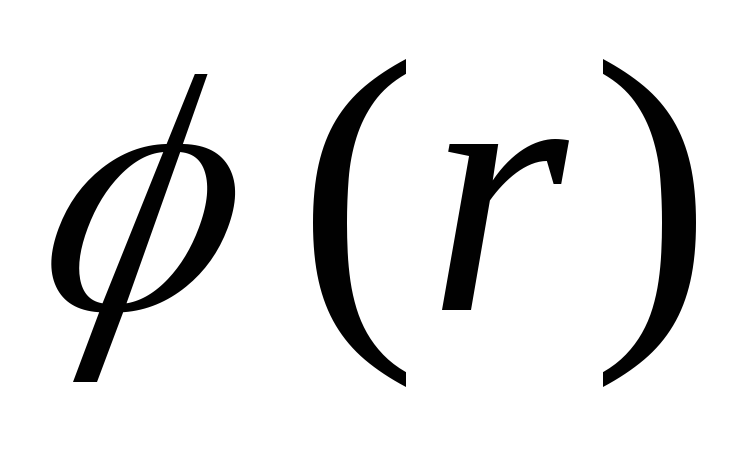 
parodyta ____ paveiksle.
Išanalizuokime gautą grafiką.
Pagal problemos būklę, už nurodytą vertę 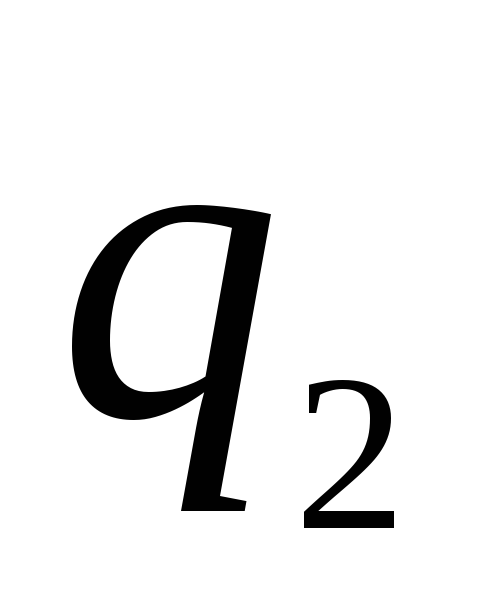potencialas vidinės sferos paviršiuje 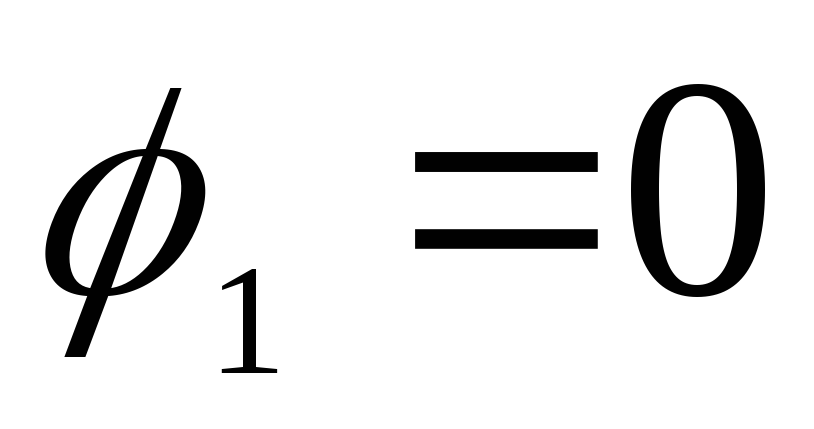. At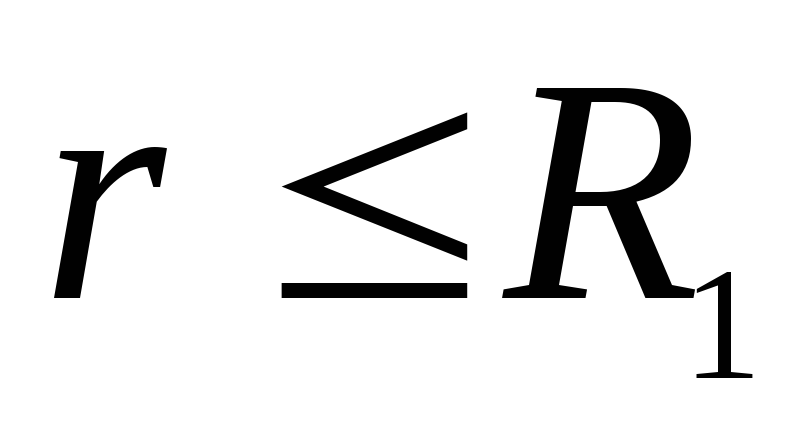 
potencialas yra pastovus ir lygus potencialui paviršiuje, todėl grafikas srityje nuo 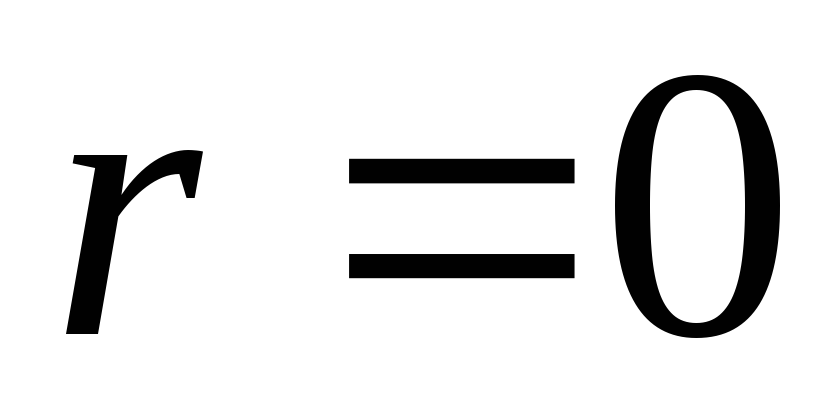prieš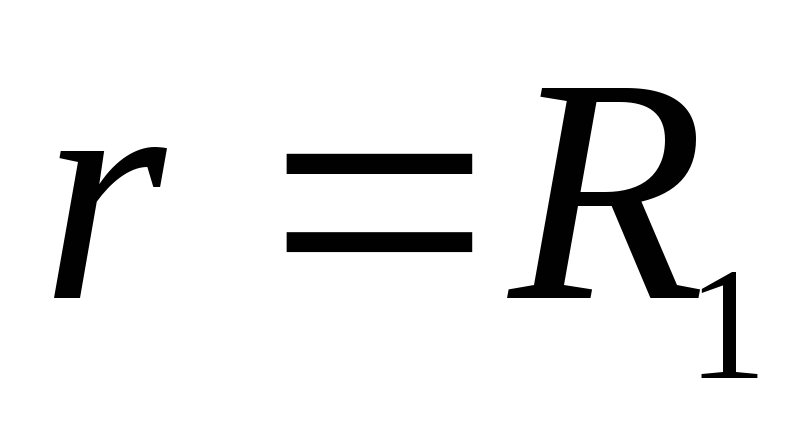 
yra tiesi linija, sutampanti su x ašimi. At 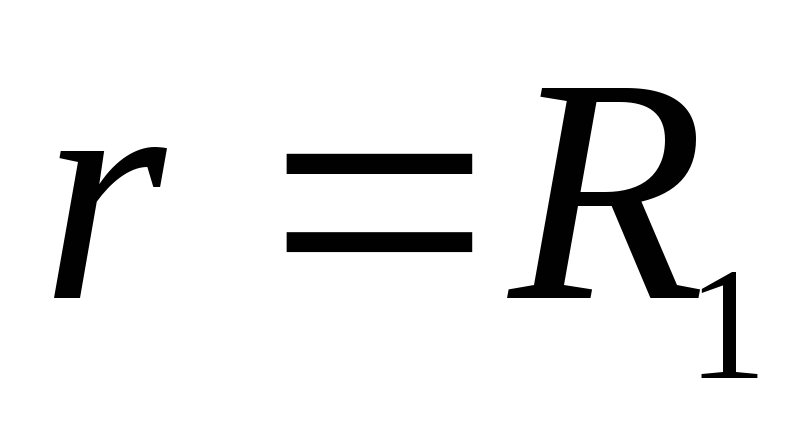vektorius patiria pertrauką. Nes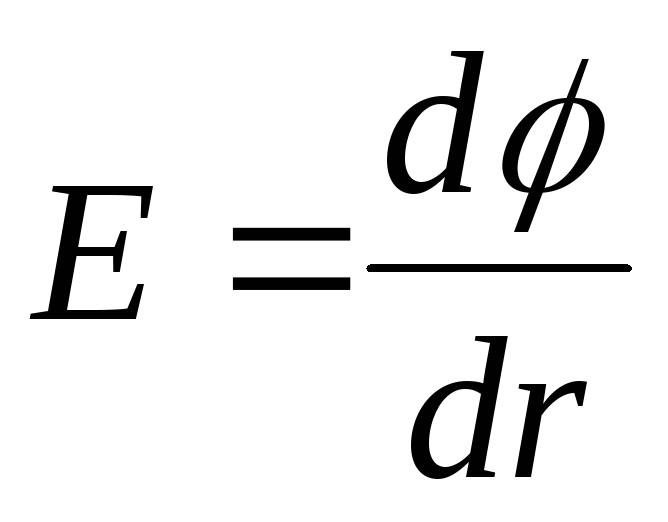 
, tada grafike taškas 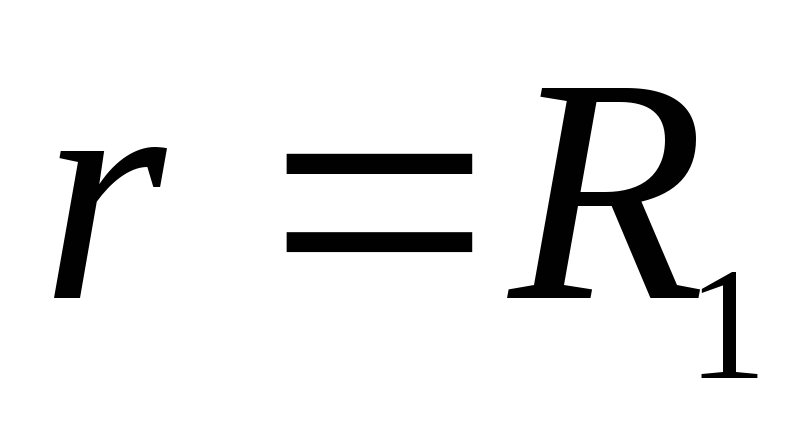(tas pats kaip taškas 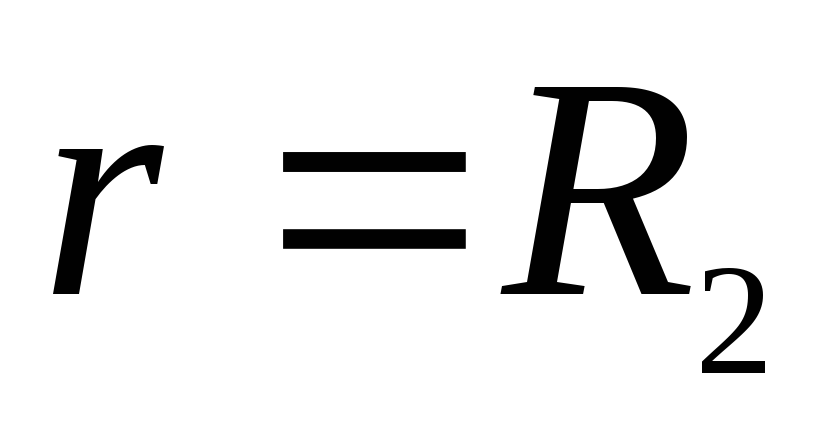) reiškia vienaskaitos taškus. Vieta įjungta 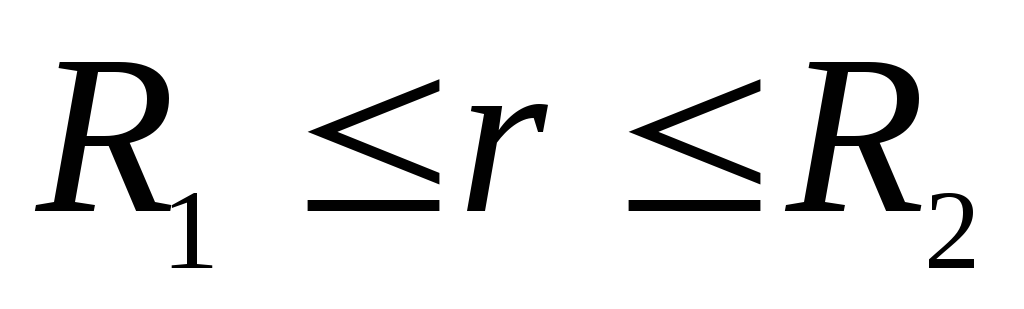vektorius nukreiptas palei spindulio vektorių 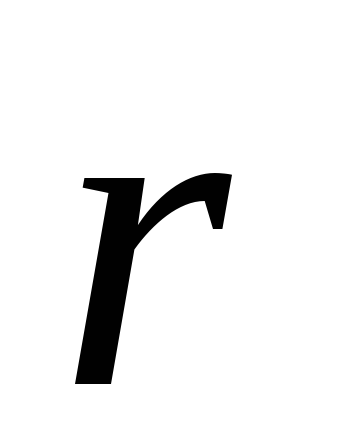. Todėl tolstant nuo vidinės sferos paviršiaus potencialas sumažėja iki tam tikros vertės 
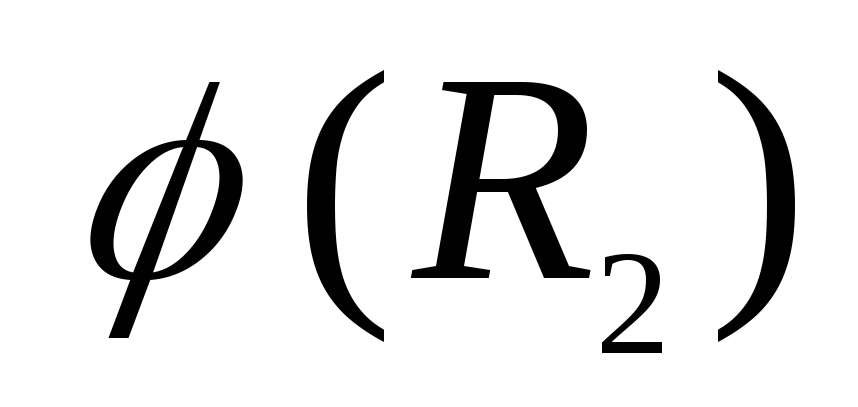. Vieta įjungta 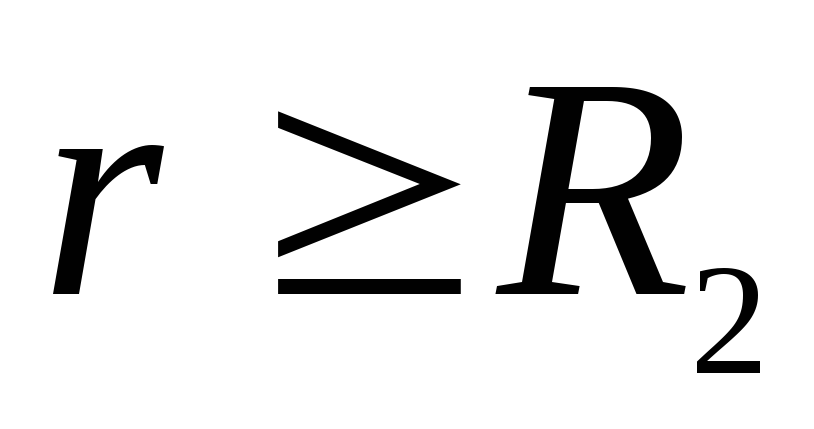vektorius nukreiptas į spindulį-vektorių 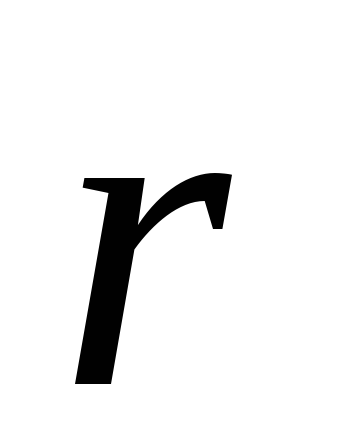, todėl, didėjant atstumui nuo išorinės sferos paviršiaus, potencialas didėja, o 
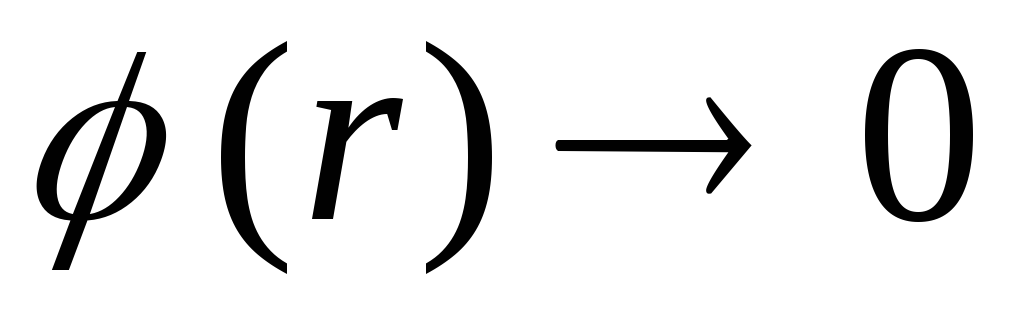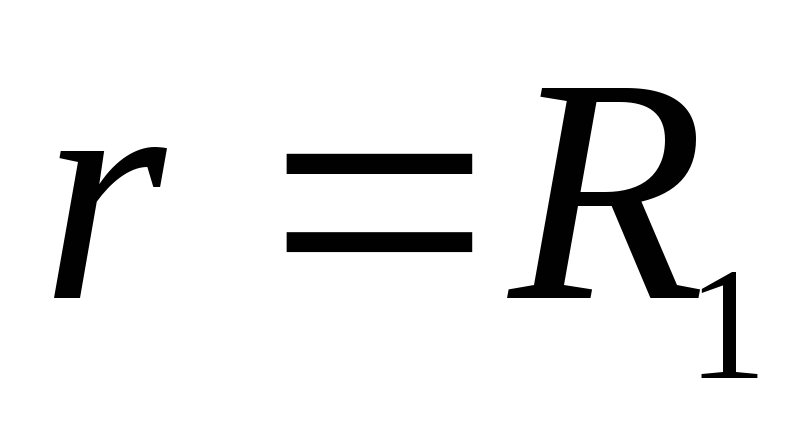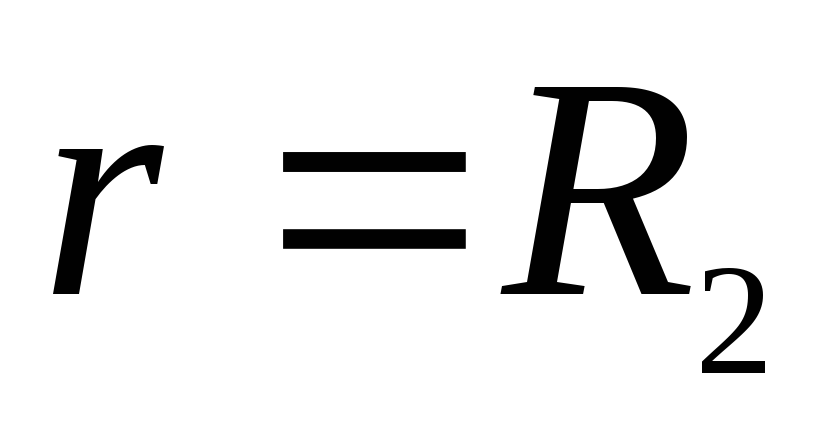. Nors taškuose ir vektorius pertraukos, funkcija 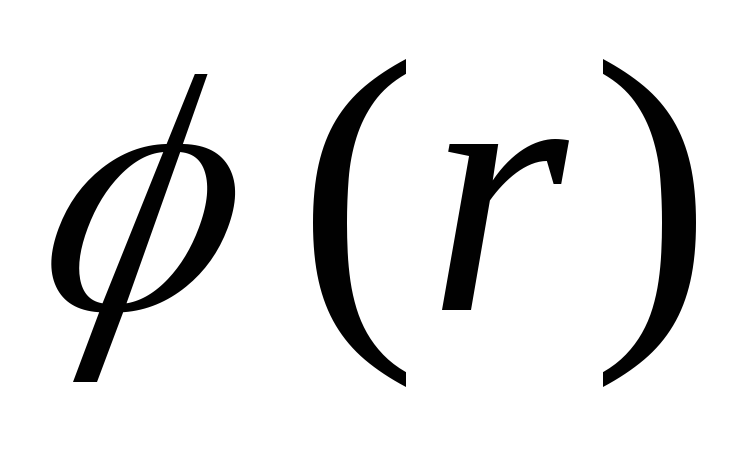yra tęstinis.
Tarp mokyklinių fizikos problemų išsiskiria tos, kurios susijusios su koncentrinėmis laidžiosiomis sferomis. Šios sferos gali būti įkraunamos, įžemintos, gali būti išorinių krūvių srityje ir pan., yra daug variantų. AT mokyklos kursas fizikos, šios problemos yra vienos sunkiausių. Paskutinis, bet ne mažiau svarbus dalykas, žinoma, šios medžiagos nesupratimas kyla dėl to, kad mokytojai nesugeba jos kompetentingai ir prieinamai paaiškinti. Taigi, pabandykime išsiaiškinti, kas yra šios laidžios sferos ir su kuo jos valgomos.
Vidinės sferos potencialas φ 2 nustatomas pagal žinomą ryšį:
Tada visas potencialas φ vidinės sferos paviršiuje yra:
Potencialas išorinės sferos paviršiuje taip pat susideda iš dviejų potencialų: vidinės sferos φ’ 1 ir tikroji išorinė sfera φ’ 2 .
Vidinės sferos potencialas φ’ 1 atstumu R nuo jo centro nustatomas žinomu ryšiu:
Formulė, kuri lemia išorinės sferos potencialą φ’ 2 ant jo paviršiaus taip pat gerai žinomas:
Tada bendras potencialas išorinės sferos paviršiuje yra:
Sprendimas. Prieš sujungiant rutulius su laidininku, pirmojo krūvis buvo lygus:
Po sujungimo dalis krūvio iš vidinės sferos tekėjo į išorinę. Srovė sustojo tuo metu, kai rutulio potencialas tapo lygus išorinio apvalkalo potencialui. Todėl patogiau ieškoti ne kamuoliuko, o jam prilyginto išorinio apvalkalo potencialo. Remiantis ankstesnėje užduotyje gautais rezultatais, šis potencialas nustatomas pagal išraišką:
kur q 1 ir q 2 - atitinkamai rutulio ir išorinio apvalkalo krūviai po jų sujungimo su laidininku. Pagal krūvio išsaugojimo dėsnį q = q 1 + q 2. Po paprastų transformacijų gauname:
Norėdami išspręsti problemą, pradėkime nuo paveikslėlio:
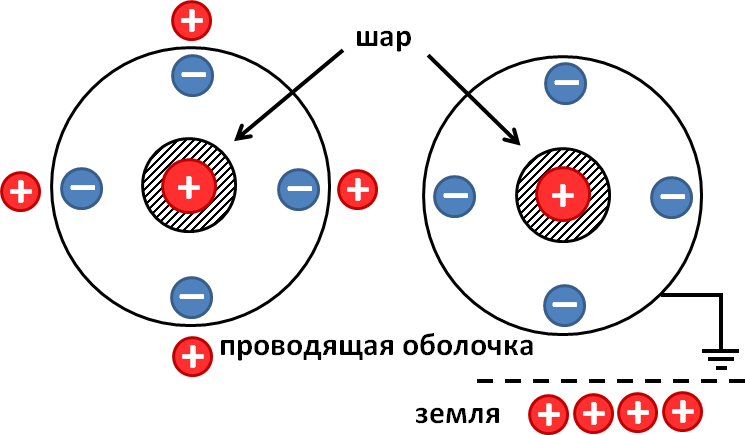
Įžeminus laidžią apvalkalą, visas teigiamas krūvis, susidaręs ant jo dėl elektrostatinės indukcijos reiškinio, nuteka į žemę. Ant jo lieka tik neigiamas krūvis, nes jį traukia teigiamas vidinės sferos krūvis
Sprendimas.Žinodami rutulio potencialą pradiniu laiko momentu ir jo spindulį, galime rasti jo krūvį:
Dėl išorinio apvalkalo elektrostatinės indukcijos reiškinio turi įvykti krūvio atsiskyrimas. Neigiamas krūvis tekės į vidinį apvalkalo paviršių, teigiamas – į išorinį (žr. pav.). Tas pats reiškinys iškilo ir ankstesnėse problemose, bet mes į tai neatsižvelgėme. Kodėl? Problemų sąlygomis buvo nurodyta, kad apvalkalas yra plonas, o toks krūvių „išbėgimas“ nepakeitė elektrostatinio lauko konfigūracijos.
Šioje užduotyje buhalterinė apskaita šis reiškinys svarbu, nes korpusas yra įžemintas. Po įžeminimo teigiamas krūvis iš korpuso nutekės į žemę, liks tik neigiamas. q 2, nes jį traukia teigiamas krūvis q 1 vidinė sfera. Įžeminto apvalkalo potencialas taps lygus žemės potencialui, tai yra nuliui. Šiuo atžvilgiu ir pagal rezultatą, gautą sprendžiant pirmąją problemą, gauname lygybę:
Naudodami tokios sistemos vidinės sferos potencialo apskaičiavimo išraišką, gautą pirmoje užduotyje, galiausiai randame reikiamą rutulio potencialą:
Patirtis rodo, kad retai kas iš pirmo karto supranta visų smulkmenų šių problemų sprendimą. Paprastai mokiniams užtrunka ilgai ir atkakliai paaiškinti visas tas smulkmenas, kurių nesuvokiant sprendimas redukuojamas į tuščias pažodinių posakių transformacijas, kad būtų gautas vadovėlio pabaigoje pateiktas atsakymas. Nelengva perprasti šių užduočių fizinę esmę ir išmokti įgytas žinias pritaikyti ateityje. Tačiau tai yra pagrindinė šios temos metodinė vertė mokykliniame fizikos kurse. Geriausias asistentas jos tyrime tikrai bus profesionalus dėstytojas, kompetentingas mentorius, galintis pateikti jums suprantamą paaiškinimą ir atsakyti į visus jūsų klausimus. Beje, jei tokių yra, galite jų paklausti žemiau komentaruose.
Sergejus Valerjevičius