Funkciju grafiks y=f(x) sauca izliekts uz intervālu (a;b), ja tas atrodas zem jebkuras tā pieskares šajā intervālā.
Funkciju grafiks y=f(x) sauca ieliekts uz intervālu (a;b), ja tas atrodas virs jebkuras tās pieskares šajā intervālā.
Attēlā parādīta līkne, kas ir izliekta uz (a;b) un ieliekts līdz (b;c).
Piemēri.
Apsveriet pietiekamu zīmi, kas ļauj noteikt, vai funkcijas grafiks noteiktā intervālā būs izliekts vai ieliekts.
Teorēma. Ļaujiet y=f(x) atšķiras ar (a;b). Ja visos intervāla punktos (a;b) otrais funkcijas atvasinājums y = f(x) negatīvs, t.i. f ""(x) < 0, то график функции на этом интервале выпуклый, если же f""(x) > 0 ir ieliekta.
Pierādījums. Pieņemsim skaidrības labad, ka f""(x) < 0 и докажем, что график функции будет выпуклым.
Paņemiet funkciju grafiku y = f(x) patvaļīgs punkts M0 ar abscisu x0 Î ( a; b) un izvelciet caur punktu M0 pieskares. Viņas vienādojums. Mums jāparāda, ka funkcijas grafiks ir (a;b) atrodas zem šīs pieskares, t.i. ar tādu pašu vērtību x līknes ordinātas y = f(x) būs mazāks par pieskares ordinātu.
Tātad līknes vienādojums ir y = f(x). Apzīmēsim pieskares ordinātu, kas atbilst abscisai x. Tad . Tāpēc starpība starp līknes ordinātām un tangensu vienā un tajā pašā vērtībā x būs .
Atšķirība f(x) – f(x0) pārveidot pēc Lagranža teorēmas, kur c starp x un x0.
Pa šo ceļu,
Mēs atkal piemērojam Lagranža teorēmu izteiksmei kvadrātiekavās: , kur c 1 starp c 0 un x0. Saskaņā ar teorēmu f ""(x) < 0. Определим знак произведения второго и третьего сомножителей.
Tādējādi jebkurš līknes punkts atrodas zem līknes pieskares visām vērtībām x un x0 Î ( a; b), kas nozīmē, ka līkne ir izliekta. Teorēmas otrā daļa ir pierādīta līdzīgi.
Piemēri.
Tiek saukts punkts nepārtrauktas funkcijas grafikā, kas atdala tās izliekto daļu no ieliektās daļas lēciena punkts.
Acīmredzot lēciena punktā pieskares, ja tāda pastāv, šķērso līkni, jo vienā šī punkta pusē līkne atrodas zem pieskares, bet otrā pusē - virs tās.
Definēsim pietiekamus nosacījumus tam, ka dots punkts līkne ir lēciena punkts.
Teorēma. Ļaujiet līkni definēt ar vienādojumu y = f(x). Ja f ""(x 0) = 0 vai f ""(x 0) neeksistē un ejot cauri vērtībai x = x0 atvasinājums f ""(x) maina zīmi, tad funkcijas grafika punkts ar abscisu x = x0 ir lēciena punkts.
Pierādījums. Ļaujiet f ""(x) < 0 при x < x0 un f ""(x) > 0 plkst x > x0. Tad plkst x < x0 līkne ir izliekta, un x > x0- ieliekts. Līdz ar to jautājums A, guļus uz izliekuma, ar abscisu x0 ir lēciena punkts. Līdzīgi varam aplūkot otro gadījumu, kad f ""(x) > 0 plkst x < x0 un f ""(x) < 0 при x > x0.
Tādējādi locījuma punkti jāmeklē tikai starp tiem punktiem, kur otrs atvasinājums pazūd vai neeksistē.
Piemēri. Atrodiet lēciena punktus un nosakiet līkņu izliekuma un ieliekuma intervālus.
FUNKCIJAS GRAFIKA ASIMPTOTI
Pētot funkciju, ir svarīgi noteikt tās grafika formu ar neierobežotu grafika punkta noņemšanu no sākuma.
Īpaši interesants ir gadījums, kad funkcijas grafiks, kad tās mainīgais punkts tiek noņemts līdz bezgalībai, neierobežoti tuvojas noteiktai taisnei.
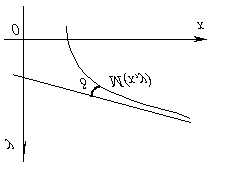
Tiešais zvans asimptote funkciju grafiks y = f(x) ja attālums no mainīgā punkta M grafikā līdz šai līnijai, kad punkts ir noņemts M līdz bezgalībai tiecas uz nulli, t.i. funkcijas grafika punktam, jo tas tiecas uz bezgalību, bezgalīgi jātuvojas asimptotam.
Līkne var tuvoties savai asimptotam, paliekot vienā tās pusē vai dažādās pusēs, bezgalīgi daudz reižu krustojot asimptotu un pārvietojoties no vienas puses uz otru.
Ja ar d apzīmējam attālumu no punkta M līkne līdz asimptotam, ir skaidrs, ka d ir tendence uz nulli, kad punkts tiek noņemts M līdz bezgalībai.
Tālāk mēs nošķirsim vertikālās un slīpās asimptotes.
VERTIKĀLIE ASIMPTOTI
Ļaujiet plkst x→ x0 abām funkcijas pusēm y = f(x) bezgalīgi palielinās absolūtajā vērtībā, t.i. vai vai 
. Tad no asimptota definīcijas izriet, ka līnija x = x0 ir asimptote. Arī otrādi ir acīmredzama, ja līnija x = x0 ir asimptote, tāpēc .
Tādējādi funkcijas grafika vertikālā asimptote y = f(x) tiek saukta par līniju, ja f(x)→ ∞ vismaz vienā no nosacījumiem x→ x0– 0 vai x → x0 + 0, x = x0
Tāpēc, lai atrastu funkcijas grafika vertikālās asimptotes y = f(x) jāatrod šīs vērtības x = x0, pie kuras funkcija iet līdz bezgalībai (cieš bezgalīgu pārtraukumu). Tad vertikālajam asimptotam ir vienādojums x = x0.
Piemēri.
SLĪPI ASIMPTOTI
Tā kā asimptote ir taisna līnija, tad, ja līkne y = f(x) ir slīps asimptote, tad tā vienādojums būs y = kx + b. Mūsu uzdevums ir atrast koeficientus k un b.
Teorēma. Taisni y = kx + b kalpo kā slīps asimptots plkst x→ +∞ funkcijas grafikam y
= f(x) ja un tikai tad 
. Līdzīgs apgalvojums attiecas uz x → –∞.
Pierādījums. Ļaujiet MP- segmenta garums, kas vienāds ar attālumu no punkta M uz asimptotu. Pēc nosacījuma. Ar φ apzīmē asimptotes slīpuma leņķi pret asi Vērsis. Tad no ΔMNP tam seko. Tā kā φ ir nemainīgs leņķis (φ ≠ π/2), tad , bet
Izmantojot tiešsaistes kalkulatoru, jūs varat atrast Funkcijas grafika lēciena punkti un izliekuma intervāli ar risinājuma noformējumu programmā Word. To, vai divu mainīgo f(x1,x2) funkcija ir izliekta, izlemj, izmantojot Hesa matricu.
Funkciju ievadīšanas noteikumi:
Funkcijas grafika izliekuma virziens. Līkuma punkti
Definīcija: Līkni y=f(x) sauc par lejupejošu izliektu intervālā (a; b), ja tā atrodas virs tangences jebkurā šī intervāla punktā.Definīcija: Līkne y=f(x) tiek saukta par augšup izliektu intervālā (a; b), ja tā atrodas zem tangences jebkurā šī intervāla punktā. 
Definīcija: Intervālus, kuros funkcijas grafiks ir izliekts uz augšu vai uz leju, sauc par funkcijas grafika izliekuma intervāliem.
Līknes, kas ir funkcijas y=f(x) grafiks, izliekumu uz leju vai uz augšu raksturo tās otrā atvasinājuma zīme: ja kādā intervālā f''(x) > 0, tad līkne ir izliekta. uz leju šajā intervālā; ja f''(x)< 0, то кривая выпукла вверх на этом промежутке.
Definīcija: Funkcijas y=f(x) grafika punktu, kas atdala šī grafika pretējo virzienu izliekuma intervālus, sauc par lēciena punktu. 
Tikai otrā veida kritiskie punkti var kalpot kā lēciena punkti; punkti, kas pieder funkcijas y = f(x) domēnam, pie kuriem otrs atvasinājums f''(x) pazūd vai saplīst.
Noteikums funkcijas grafika lēciena punktu atrašanai y = f(x)
- Atrodiet otro atvasinājumu f''(x) .
- Atrodiet funkcijas y=f(x) otrā veida kritiskos punktus, t.i. punkts, kurā f''(x) pazūd vai pārtrūkst.
- Pētīt otrā atvasinājuma f''(x) zīmi intervālos, kuros atrastie kritiskie punkti sadala funkcijas f(x) apgabalu. Ja šajā gadījumā kritiskais punkts x 0 atdala pretējo virzienu izliekuma intervālus, tad x 0 ir funkcijas grafika lēciena punkta abscisa.
- Aprēķiniet funkciju vērtības lēciena punktos.
1. piemērs. Atrodiet šādas līknes izliekuma spraugas un lēciena punktus: f(x) = 6x 2 –x 3 .
Risinājums: atrodiet f '(x) = 12x - 3x 2, f ''(x) = 12 - 6x.
Atradīsim kritiskos punktus pēc otrā atvasinājuma, atrisinot vienādojumu 12-6x=0 . x=2. 
f(2) = 6 * 2 2 - 2 3 = 16
Atbilde: Funkcija ir uz augšu izliekta x∈(2; +∞) ; funkcija ir uz leju izliekta x∈(-∞; 2) ; lēciena punkts (2;16) .
2. piemērs. Vai funkcijai ir lēciena punkti: f(x)=x 3 -6x 2 +2x-1
3. piemērs. Atrodiet intervālus, kuros funkcijas grafiks ir izliekts un izliekts: f(x)=x 3 -6x 2 +12x+4
ir diferencējams intervālā (a, c). Tad funkcijas grafikam jebkurā punktā ir pieskare 
šis grafiks ( 
), un pieskare nav paralēla OY asij, jo tās slīpums ir vienāds ar 
, protams.
definīcija
uz (a, c) ir izlaidums, kas vērsts uz leju (uz augšu), ja tas neatrodas zem (ne virs) jebkuras pieskares funkcijas grafikam uz (a, c). 
(
) visos šī intervāla punktos, tad līkne, kas ir funkcijas grafiks, šajā intervālā ir izliekta (ieliekta).
sauc par funkcijas grafika lēciena punktu, ja punktā 
grafikā ir pieskare, un ir tāda punkta apkārtne 
, kurā funkcijas grafikam pa kreisi un pa labi no punkta ir dažādi izliekuma virzieni.
ir acīmredzams, ka lēciena punktā tangenss šķērso funkcijas grafiku, jo vienā šī punkta pusē grafiks atrodas virs pieskares, bet otrā - zem tā, t.i., lēciena punkta tuvumā, funkcijas grafiks ģeometriski pāriet no vienas pieskares puses uz otru un "izliecas" caur to. No šejienes cēlies nosaukums "locījuma punkts".
nepārtraukts otrais atvasinājums. Tad 
.
nav lēciena punkta pie (0, 0), lai gan 
plkst 
. Tāpēc otrā atvasinājuma vienādība ar nulli ir tikai nepieciešams nosacījums locījumam. 
Tā ir 
ir otrs atvasinājums kādā punkta apkārtnē, izņemot pašu punktu, un funkcijas grafikam punktā ir pieskare. 
. Tad, ja norādītajā apkārtnē tai ir dažādas zīmes pa kreisi un pa labi no punkta , tad funkcijas grafikā ir locījums punktā . 
izliekums, ieliekums, lēciena punkti. 
, 
=
neeksistē plkst 
)
)
vai tuvu 2. veida pārrāvuma punktiem, bieži vien izrādās, ka funkcijas grafiks tuvojas vienai vai otrai taisnei, cik tuvu vien patīk. Šādas līnijas sauc.
definīcija 1.
sauc par līknes L asimptotu, ja attālumam no līknes punkta līdz šai taisnei ir tendence uz nulli, punktam attālinoties pa līkni līdz bezgalībai. Ir trīs veidu asimptoti: vertikāli, horizontāli, slīpi. 
sauc par funkcijas grafika vertikālo asimptotu, ja vismaz viena no vienpusējām robežām ir vienāda ar 
, t.i., vai 
ir vertikāla asimptota 
, jo 
, a 
.
ja 
.
.
(
) sauc par funkcijas grafika slīpo asimptotu 
ja 
; 
.
; x=0 – vertikālā asimptote
.
ir slīpa asimptote. 
un uzzīmējiet to. 
funkcija nav ne pāra, ne nepāra-
-
+
+
y
-4
t r.
0
Secinājums.
Svarīga aplūkotās metodes iezīme ir tā, ka tā galvenokārt balstās uz līknes uzvedības raksturīgo pazīmju noteikšanu un izpēti. Vietas, kur vienmērīgi mainās funkcija, netiek īpaši detalizēti pētītas, un šāda izpēte nav nepieciešama. Bet tās vietas, kur funkcijai ir kādas uzvedības īpatnības, ir pakļautas pilnīgai izpētei un visprecīzākajam grafiskajam attēlojumam. Šīs pazīmes ir maksimālās, minimālās, funkcijas pārtraukuma punkti utt.
Ieliekuma un locījumu virziena noteikšana, kā arī norādītā asimptotu atrašanas metode ļauj vēl detalizētāk izpētīt funkcijas un iegūt precīzāku priekšstatu par to grafikiem.
Funkcijas izliekuma jēdziens
Apsveriet funkciju \(y = f\left(x \right),\), kas tiek pieņemta kā nepārtraukta segmentā \(\left[ (a,b) \right].\) Funkcija \(y = f \left(x \right),\) )\) tiek izsaukts izliekts uz leju (vai vienkārši izliekts) ja jebkuram punktam \((x_1)\) un \((x_2)\) no \(\left[ (a,b) \right]\) x_1),(x_2) \in \left[ (a, b) \right],\) tā, ka \((x_1) \ne (x_2),\) tad tiek izsaukta funkcija \(f\left(x \right) \) stingri izliekta uz leju
Uz augšu izliekta funkcija tiek definēta līdzīgi. Tiek izsaukta funkcija \(f\left(x \right)\). izliekts uz augšu (vai ieliekts) ja jebkuram segmenta \((x_2)\) punktiem \((x_1)\) un \((x_2)\) nevienādība \ Ja šī nevienlīdzība ir strikta jebkuram \( ( x_1),(x_2) \in \left[ (a,b) \right],\) tā, lai \((x_1) \ne (x_2),\) pēc tam funkcija \(f\left(x \right) ) \) tiek saukti stingri izliekta uz augšu segmentā \(\left[ (a,b) \right].\)
Funkcijas izliekuma ģeometriskā interpretācija
Ieviestajām izliektās funkcijas definīcijām ir vienkārša ģeometriskā interpretācija.
Funkcijai, izliekts uz leju (zīmējums \(1\)), jebkura horda \((A_1)(A_2)\) viduspunkts \(B\) atrodas virs
Līdzīgi funkcijai izliekts uz augšu (zīmējums \(2\)), jebkura horda \((A_1)(A_2)\) viduspunkts \(B\) atrodas zemāk funkcijas grafika atbilstošais punkts \((A_0)\) vai sakrīt ar šo punktu.
Izliektajām funkcijām ir vēl viens vizuāls īpašums, kas ir saistīts ar atrašanās vietu pieskares uz funkcijas grafiku. Funkcija \(f\left(x \right)\) ir izliekts uz leju segmentā \(\left[ (a,b) \right]\) tad un tikai tad, ja tā grafiks nav zemāks par pieskari, kas tam novilkta jebkurā segmenta \(\left) punktā \((x_0)\) [ (a ,b) \pa labi]\) (attēls \(3\)).
Attiecīgi funkcija \(f\left(x \right)\) ir izliekts uz augšu segmentā \(\left[ (a,b) \right]\) tad un tikai tad, ja tā grafiks nav augstāks par pieskari, kas tam novilkta jebkurā segmenta \(\left) punktā \((x_0)\) [ (a ,b) \pa labi]\) (attēls \(4\)). Šīs īpašības ir teorēma, un tās var pierādīt, izmantojot funkcijas izliekuma definīciju.
Pietiekami apstākļi izliekumam
Ļaujiet funkcijai \(f\left(x \right)\) pirmais atvasinājums \(f"\left(x \right)\) pastāvēt segmentā \(\left[ (a,b) \right], \) un otrais atvasinājums \(f""\left(x \right)\) − intervālā \(\left((a,b) \right).\) Tad tiek ievēroti šādi pietiekami izliekuma kritēriji:
Ja \(f""\left(x \right) \ge 0\) visiem \(x \in \left((a,b) \right),\), tad funkcija \(f\left(x \) pareizi )\) izliekts uz leju segmentā \(\left[ (a,b) \right];\)
Ja \(f""\left(x \right) \le 0\) visiem \(x \in \left((a,b) \right),\), tad funkcija \(f\left(x \) pareizi )\) izliekts uz augšu segmentā \(\left[ (a,b) \right].\)
Pierādīsim augstāk minēto teorēmu lejupejošas izliektas funkcijas gadījumā. Lai funkcijai \(f\left(x \right)\) ir nenegatīvs otrais atvasinājums intervālā \(\left((a,b) \right):\) \(f""\left(x) \right) \ge 0.\) Apzīmējiet ar \((x_0)\) segmenta viduspunktu \(\left[ ((x_1),(x_2)) \right].\) Pieņemsim, ka šī segmenta garums ir vienāds ar \(2h.\) Tad koordinātas \((x_1)\) un \((x_2)\) var uzrakstīt šādi: \[(x_1) = (x_0) - h,\;\;(x_2 ) = (x_0) + h.\] Izvērsiet funkciju \(f\left(x \right)\) punktā \((x_0)\) Teilora sērijā ar atlikušo terminu Lagranža formā. Mēs iegūstam šādas izteiksmes: \[ (f\left(((x_1)) \right) = f\left(((x_0) - h) \right) ) = (f\left(((x_0)) \right ) - f"\left(((x_0)) \right)h + \frac((f""\left(((\xi _1)) \right)(h^2)))((2},}
\]
\[
{f\left({{x_2}} \right) = f\left({{x_0} + h} \right) }
= {f\left({{x_0}} \right) + f"\left({{x_0}} \right)h + \frac{{f""\left({{\xi _2}} \right){h^2}}}{{2!}},}
\]
где \({x_0} - h !}
Pievienojiet abas vienādības: \[ (f\left(((x_1)) \right) + f\left(((x_2)) \right) ) = (2f\left(((x_0)) \right) + \frac (((h^2)))(2)\left[ (f""\left(((\xi _1)) \right) + f""\left(((\xi _2)) \right)) \right].) \] Tā kā \((\xi _1),(\xi _2) \in \left((a,b) \right),\), otrie atvasinājumi labajā pusē nav negatīvi . Tāpēc \ vai \, kas saskaņā ar definīciju ir funkcija \(f\left(x \right)\) izliekts uz leju
.
Ņemiet vērā, ka nepieciešamais funkcijas izliekuma nosacījums (t.i., tiešā teorēma, kurā, piemēram, no izliekuma nosacījuma izriet, ka \(f""\left(x \right) \ge 0\)) ir izpildīts tikai tad, ja nevienlīdzība. Stingras izliekuma gadījumā nepieciešamais nosacījums parasti nav izpildīts. Piemēram, funkcija \(f\left(x \right) = (x^4)\) ir stingri uz leju izliekta. Tomēr punktā \(x = 0\) tā otrais atvasinājums ir vienāds ar nulli, t.i. striktā nevienādība \(f""\left(x \right) \gt 0\) šajā gadījumā nav izpildīta.
Izliekto funkciju īpašības
Mēs uzskaitām dažas izliekto funkciju īpašības, pieņemot, ka visas funkcijas ir definētas un nepārtrauktas segmentā \(\left[ (a,b) \right].\)
Ja funkcijas \(f\) un \(g\) ir lejup (augšup) izliektas, tad jebkura no tām lineāra kombinācija \(af + bg,\) kur \(a\), \(b\) ir pozitīvi reāli skaitļi, arī izliekti uz leju (augšup).
Ja funkcija \(u = g\left(x \right)\) ir uz leju izliekta un funkcija \(y = f\left(u \right)\) ir uz leju izliekta un nesamazinās, tad sarežģīta funkcija \(y = f\left((g\left(x \right)) \right)\) arī būs izliekta uz leju.
Ja funkcija \(u = g\left(x \right)\) ir uz augšu izliekta un funkcija \(y = f\left(u \right)\) ir uz leju izliekta un nepalielinās, tad sarežģīta funkcija \(y = f\left((g\left(x \right)) \right)\) būs izliekta uz leju.
Vietējais maksimums izliekta augšupvērsta funkcija, kas definēta segmentā \(\left[ (a,b) \right],\) ir vienlaikus tās augstākā vērtība šajā segmentā.
Vietējais minimums uz leju izliekta funkcija, kas definēta segmentā \(\left[ (a,b) \right],\) vienlaikus ir tā mazākā vērtība šajā segmentā.
Uzzīmējot funkciju, ir svarīgi definēt izliektos intervālus un lēciena punktus. Mums tie ir nepieciešami kopā ar samazinājuma un palielināšanas intervāliem, lai skaidri attēlotu funkciju grafiskā formā.
Lai izprastu šo tēmu, ir jāzina, kas ir funkcijas atvasinājums un kā to aprēķināt noteiktā secībā, kā arī jāprot atrisināt dažādi veidi nevienlīdzības.
Raksta sākumā ir definēti galvenie jēdzieni. Tad mēs parādīsim, kāda saistība pastāv starp izliekuma virzienu un otrā atvasinājuma vērtību noteiktā intervālā. Tālāk mēs norādīsim nosacījumus, kādos var noteikt grafika lēciena punktus. Visa argumentācija tiks ilustrēta ar problēmu risinājumu piemēriem.
1. definīcijaUz leju noteiktā intervālā gadījumā, ja tā grafiks atrodas ne zemāk par pieskari tam jebkurā šī intervāla punktā.
2. definīcija
Diferencējamā funkcija ir izliekta uz augšu noteiktā intervālā, ja šīs funkcijas grafiks neatrodas augstāk par tās pieskari jebkurā šī intervāla punktā.
Uz leju izliektu funkciju var saukt arī par ieliektu. Abas definīcijas ir skaidri parādītas zemāk esošajā diagrammā:
3. definīcija
Funkcijas lēciena punkts- tas ir punkts M (x 0 ; f (x 0)) , kurā funkcijas grafikam ir pieskare, ar nosacījumu, ka atvasinājums eksistē punkta x 0 tuvumā, kur funkcijas grafiks aizņem dažādus izliekuma virzienus kreisajā un labajā pusē.
Vienkārši sakot, lēciena punkts ir vieta grafikā, kur ir pieskare, un grafa izliekuma virziens, ejot cauri šai vietai, mainīs izliekuma virzienu. Ja neatceraties, kādos apstākļos ir iespējama vertikālās un nevertikālās pieskares pastāvēšana, iesakām atkārtot sadaļu par funkcijas grafika pieskares punktu punktā.
Tālāk ir redzams funkcijas grafiks, kurā ir vairāki lēciena punkti, kas iezīmēti sarkanā krāsā. Precizēsim, ka locījuma punktu klātbūtne nav obligāta. Vienas funkcijas grafikā var būt viena, divas, vairākas, bezgalīgi daudz vai neviena.
Šajā sadaļā mēs runāsim par teorēmu, ar kuras palīdzību jūs varat noteikt izliekuma intervālus konkrētas funkcijas grafikā.
4. definīcija
Funkcijas grafikam būs izliekums virzienā uz leju vai uz augšu, ja attiecīgajai funkcijai y = f (x) ir otrs galīgs atvasinājums norādītajā intervālā x ar nosacījumu, ka nevienādība f "" (x) ≥ 0 ∀ x ∈ X (f "" (x) ≤ 0 ∀ x ∈ X) būs patiess.
Izmantojot šo teorēmu, jūs varat atrast ieliekuma un izliekuma intervālus jebkurā funkcijas grafikā. Lai to izdarītu, jums vienkārši jāatrisina nevienādības f "" (x) ≥ 0 un f "" (x) ≤ 0 atbilstošās funkcijas domēnā.
Precizēsim, ka tie punkti, kuros otrā atvasinājuma nav, bet ir definēta funkcija y = f (x), tiks iekļauti izliekuma un ieliekuma intervālos.
Apskatīsim piemēru konkrēts uzdevums kā pareizi pielietot šo teorēmu.
1. piemērs
Stāvoklis: dota funkcija y = x 3 6 - x 2 + 3 x - 1 . Nosakiet, kādos intervālos tā grafikam būs izliekums un ieliekums.
Risinājums
Šīs funkcijas domēns ir visa reālo skaitļu kopa. Sāksim ar otrā atvasinājuma aprēķināšanu.
y "= x 3 6 - x 2 + 3 x - 1" = x 2 2 - 2 x + 3 ⇒ y "" = x 2 2 - 2 x + 3 = x - 2
Mēs redzam, ka otrā atvasinājuma apgabals sakrita ar pašas funkcijas domēnu, tāpēc, lai identificētu izliekuma intervālus, jāatrisina nevienādības f "" (x) ≥ 0 un f "" (x) ≤ 0 .
y "" ≥ 0 ⇔ x - 2 ≥ 0 ⇔ x ≥ 2 y "" ≤ 0 ⇔ x - 2 ≤ 0 ⇔ x ≤ 2
Ieguvām, ka dotās funkcijas grafam segmentā būs ieliekums [2; + ∞) un segmenta izliekums (- ∞ ; 2 ] .
Skaidrības labad mēs uzzīmēsim funkcijas grafiku un iezīmēsim tajā izliekto daļu ar zilu krāsu, bet ieliekto daļu ar sarkanu.
Atbilde: dotās funkcijas grafikā segmentā būs ieliekums [2; + ∞) un segmenta izliekums (- ∞ ; 2 ] .
Bet ko darīt, ja otrā atvasinājuma domēns nesakrīt ar funkcijas domēnu? Šeit mums noder iepriekš izteiktā piezīme: tos punktus, kuros galīgā otrā atvasinājuma nav, iekļausim arī ieliekuma un izliekuma segmentos.
2. piemērs
Stāvoklis: dota funkcija y = 8 x x - 1 . Nosakiet, kādos intervālos tā grafiks būs ieliekts un kādos intervālos tas būs izliekts.
Risinājums
Vispirms noskaidrosim funkcijas darbības jomu.
x ≥ 0 x - 1 ≠ 0 ⇔ x ≥ 0 x ≠ 1 ⇔ x ∈ [ 0 ; 1) ∪ (1; + ∞)
Tagad mēs aprēķinām otro atvasinājumu:
y "= 8 x x - 1" = 8 1 2 x (x - 1) - x 1 (x - 1) 2 = - 4 x + 1 x (x - 1) 2 y "" = - 4 x + 1 x (x - 1) 2 "= - 4 1 x x - 1 2 - (x + 1) x x - 1 2" x (x - 1) 4 = = - 4 1 x x - 1 2 - x + 1 1 2 x ( x - 1) 2 + x 2 (x - 1) x x - 1 4 = = 2 3 x 2 + 6 x - 1 x 3 2 (x - 1) 3
Otrā atvasinājuma apgabals ir kopa x ∈ (0 ; 1) ∪ (1 ; + ∞) . Mēs redzam, ka x vienāds ar nulli būs sākotnējās funkcijas domēnā, bet ne otrā atvasinājuma domēnā. Šis punkts ir jāiekļauj ieliekuma vai izliekuma segmentā.
Pēc tam mums ir jāatrisina nevienādības f "" (x) ≥ 0 un f "" (x) ≤ 0 uz dotās funkcijas domēna. Šim nolūkam mēs izmantojam intervāla metodi: pie x \u003d - 1 - 2 3 3 ≈ - 2, 1547 vai x \u003d - 1 + 2 3 3 ≈ 0, 1547 skaitītājs 2 (3 x 2 + 6 x - 1) x 2 3 x - 1 3 kļūst par 0 un saucējs ir 0, ja x ir nulle vai viens.
Ievietosim iegūtos punktus grafikā un noteiksim izteiksmes zīmi visos intervālos, kas tiks iekļauti sākotnējās funkcijas domēnā. Diagrammā šis apgabals ir norādīts ar izšķilšanos. Ja vērtība ir pozitīva, atzīmējiet intervālu ar plus, ja negatīvs, tad ar mīnusu.
Sekojoši,
f "" (x) ≥ 0 x ∈ [ 0 ; 1) ∪ (1 ; + ∞) ⇔ x ∈ 0 ; - 1 + 2 3 3 ∪ (1 ; + ∞) un f "" (x) ≤ 0 x ∈ [ 0 ; 1) ∪ (1 ; + ∞) ⇔ x ∈ [ - 1 + 2 3 3 ; viens)
Ieslēdzam iepriekš atzīmēto punktu x = 0 un iegūstam vēlamo atbildi. Sākotnējās funkcijas grafikā būs lejupvērsts izliekums pie 0 ; - 1 + 2 3 3 ∪ (1 ; + ∞) un uz augšu par x ∈ [ - 1 + 2 3 3 ; viens).
Uzzīmēsim grafiku, izliekto daļu atzīmējot ar zilu, bet ieliekto ar sarkanu. Vertikālā asimptote atzīmēta ar melnu punktētu līniju.
Atbilde: Sākotnējās funkcijas grafikā būs lejupvērsts izliekums pie 0 ; - 1 + 2 3 3 ∪ (1 ; + ∞) un uz augšu par x ∈ [ - 1 + 2 3 3 ; viens).
Funkciju grafika locīšanas nosacījumi
Sāksim ar vajadzīgā nosacījuma formulēšanu kādas funkcijas grafika locījumam.
5. definīcija
Pieņemsim, ka mums ir funkcija y = f(x), kuras grafikam ir lēciena punkts. Ja x = x 0, tam ir nepārtraukts otrais atvasinājums, tāpēc vienādība f "" (x 0) = 0 būs spēkā.
Ņemot vērā šo nosacījumu, mums vajadzētu meklēt lēciena punktus starp tiem, kuros otrais atvasinājums kļūs par 0. Ar šo nosacījumu nepietiks: ne visi šādi punkti mums derēs.
Ņemiet vērā arī to, ka saskaņā ar vispārējo definīciju mums būs nepieciešama pieskares līnija, vertikāla vai nevertikāla. Praksē tas nozīmē, ka, lai atrastu lieces punktus, jāņem tie, kuros šīs funkcijas otrais atvasinājums kļūst par 0. Tāpēc, lai atrastu lēciena punktu abscises, mums ir jāņem visi x 0 no funkcijas domēna, kur lim x → x 0 - 0 f " (x) = ∞ un lim x → x 0 + 0 f " (x) = ∞ . Visbiežāk tie ir punkti, kuros pirmā atvasinājuma saucējs kļūst par 0.
Pirmais pietiekošais nosacījums funkcijas grafika lēciena punkta pastāvēšanai
Mēs esam atraduši visas x 0 vērtības, kuras var uzskatīt par lēciena punktu abscisu. Pēc tam mums jāpiemēro pirmais pietiekami locījuma nosacījums.
6. definīcija
Pieņemsim, ka mums ir funkcija y = f (x), kas ir nepārtraukta punktā M (x 0 ; f (x 0)) . Turklāt tai šajā punktā ir tangenss, un pašai funkcijai ir otrs atvasinājums šī punkta x 0 tuvumā. Šajā gadījumā, ja otrais atvasinājums iegūst pretējas zīmes kreisajā un labajā pusē, tad šo punktu var uzskatīt par lēciena punktu.
Mēs redzam, ka šis nosacījums neprasa, lai otrs atvasinājums noteikti būtu šajā punktā, pietiek ar to, ka tas atrodas punkta x 0 tuvumā.
Visu iepriekš minēto var ērti attēlot kā darbību secību.
- Vispirms jāatrod visas iespējamo lēciena punktu abscises x 0, kur f "" (x 0) = 0, lim x → x 0 - 0 f "(x) = ∞, lim x → x 0 + 0 f " (x) = ∞ .
- Uzziniet, kādos punktos atvasinājums mainīs zīmi. Šīs vērtības ir lēciena punktu abscises, un tiem atbilstošie punkti M (x 0 ; f (x 0)) ir paši lēciena punkti.
Skaidrības labad apskatīsim divas problēmas.
3. piemērs
Stāvoklis: dota funkcija y = 1 10 x 4 12 - x 3 6 - 3 x 2 + 2 x . Nosakiet, kur šīs funkcijas grafikā būs lieces un izliekuma punkti.
Risinājums
Šī funkcija ir definēta visai reālo skaitļu kopai. Mēs uzskatām pirmo atvasinājumu:
y "= 1 10 x 4 12 - x 3 6 - 3 x 2 + 2 x" = 1 10 4 x 3 12 - 3 x 2 6 - 6 x + 2 = = 1 10 x 3 3 - x 2 2 - 6 x + 2
Tagad atradīsim pirmā atvasinājuma domēnu. Tā ir arī visu reālo skaitļu kopa. Tādējādi vienādības lim x → x 0 - 0 f "(x) = ∞ un lim x → x 0 + 0 f" (x) = ∞ nevar izpildīt nevienai x 0 vērtībai.
Mēs aprēķinām otro atvasinājumu:
y "" = = 1 10 x 3 3 - x 2 2 - 6 x + 2 " = 1 10 3 x 2 3 - 2 x 2 - 6 = 1 10 x 2 - x - 6
y "" = 0 ⇔ 1 10 (x 2 - x - 6) = 0 ⇔ x 2 - x - 6 = 0 D = (- 1) 2 - 4 1 (- 6) = 25 x 1 = 1 - 25 2 \u003d - 2, x 2 \u003d 1 + 25 2 \u003d 3
Mēs atradām divu iespējamo lēciena punktu - 2 un 3 - abscises. Mums atliek tikai pārbaudīt, kurā brīdī atvasinājums maina savu zīmi. Uzzīmēsim skaitlisko asi un uzzīmēsim uz tās šos punktus, pēc tam uz iegūtajiem intervāliem novietosim otrā atvasinājuma zīmes.
Loki parāda grafika izliekuma virzienu katrā intervālā.
Otrais atvasinājums apgriež zīmi (no plusa uz mīnusu) punktā ar abscisu 3, ejot cauri tam no kreisās puses uz labo, un dara to pašu (no mīnusa uz plusu) punktā ar abscisu 3. Tātad, mēs varam secināt, ka x = - 2 un x = 3 ir funkcijas grafika lēciena punktu abscises. Tie atbildīs grafika punktiem - 2; - 4 3 un 3 ; - 15 8 .
Vēlreiz apskatīsim skaitliskās ass attēlu un no tā izrietošās zīmes uz intervāliem, lai izdarītu secinājumus par ieliekuma un izliekuma vietām. Izrādās, ka izspiedums atradīsies uz segmenta - 2; 3, un ieliekums uz segmentiem (-∞;-2] un [3; + ∞).
Problēmas risinājums ir skaidri parādīts grafikā: zilā krāsa - izliekums, sarkanā - ieliekums, melnā krāsa nozīmē lieces punktus.
Atbilde: izspiedums atradīsies uz segmenta - 2; 3, un ieliekums uz segmentiem (-∞;-2] un [3; + ∞).
4. piemērs
Stāvoklis: aprēķiniet funkcijas y = 1 8 · x 2 + 3 x + 2 · x - 3 3 5 grafika visu lēciena punktu abscises.
Risinājums
Dotās funkcijas domēns ir visu reālo skaitļu kopa. Mēs aprēķinām atvasinājumu:
y "= 1 8 (x 2 + 3 x + 2) x - 3 3 5" = = 1 8 x 2 + 3 x + 2 " (x - 3) 3 5 + (x 2 + 3 x + 2) x - 3 3 5 " = = 1 8 2 x + 3 (x - 3) 3 5 + (x 2 + 3 x + 2) 3 5 x - 3 - 2 5 = 13 x 2 - 6 x - 39 40 (x - 3) 25
Atšķirībā no funkcijas, tās pirmais atvasinājums netiks noteikts ar x vērtību 3, bet:
lim x → 3 - 0 y "(x) = 13 (3 - 0) 2 - 6 (3 - 0) - 39 40 3 - 0 - 3 2 5 = + ∞ lim x → 3 + 0 y " (x) = 13 (3 + 0) 2 - 6 (3 + 0) - 39 40 3 + 0 - 3 2 5 = + ∞
Tas nozīmē, ka grafa vertikālā pieskare iet caur šo punktu. Tāpēc 3 var būt lēciena punkta abscisa.
Mēs aprēķinām otro atvasinājumu. Mēs atrodam arī tā definīcijas apgabalu un punktus, kuros tas pārvēršas par 0:
y "" = 13 x 2 - 6 x - 39 40 x - 3 2 5 " = = 1 40 13 x 2 - 6 x - 39 " (x - 3) 2 5 - 13 x 2 - 6 x - 39 x - 3 2 5 " (x - 3) 4 5 = = 1 25 13 x 2 - 51 x + 21 (x - 3) 7 5 , x ∈ (- ∞ ; 3) ∪ (3 ; + ∞ ) y "" ( x) = 0 ⇔ 13 x 2 - 51 x + 21 = 0 D = (- 51) 2 - 4 13 21 = 1509 x 1 = 51 + 1509 26 ≈ 3 , 4556 , x 2 = 51 - 1509 ≈ 5 .
Mums ir vēl divi iespējamie lēciena punkti. Mēs tos visus ievietojam skaitļu rindā un iegūtos intervālus atzīmējam ar zīmēm:
Zīmes maiņa notiks, ejot cauri katram norādītajam punktam, kas nozīmē, ka tie visi ir lēciena punkti.
Atbilde: Uzzīmēsim funkcijas grafiku, iezīmējot ieliekumus ar sarkanu, izliekumu ar zilu un lēciena punktus ar melnu:
Zinot pirmo pietiekamo locīšanas nosacījumu, varam noteikt nepieciešamos punktus, kuros otrā atvasinājuma klātbūtne nav nepieciešama. Pamatojoties uz to, pirmo nosacījumu var uzskatīt par universālāko un piemērotāko dažāda veida problēmu risināšanai.
Ņemiet vērā, ka ir vēl divi lēciena nosacījumi, taču tos var piemērot tikai tad, ja norādītajā punktā ir galīgs atvasinājums.
Ja mums ir f "" (x 0) = 0 un f """ (x 0) ≠ 0 , tad x 0 būs grafika y = f (x) lēciena punkta abscisa.
5. piemērs
Stāvoklis: ir dota funkcija y = 1 60 x 3 - 3 20 x 2 + 7 10 x - 2 5. Nosakiet, vai funkcijas grafam būs locījums 3. punktā; 4 5 .
Risinājums
Vispirms ir jāpārliecinās, vai dotais punkts vispār piederēs šīs funkcijas grafikam.
y (3) = 1 60 3 3 - 3 20 3 2 - 2 5 = 27 60 - 27 20 + 21 10 - 2 5 = 9 - 27 + 42 - 8 20 = 4 5
Norādītā funkcija ir definēta visiem argumentiem, kas ir reāli skaitļi. Mēs aprēķinām pirmo un otro atvasinājumu:
y "= 1 60 x 3 - 3 20 x 2 + 7 10 x - 2 5" = 1 20 x 2 - 3 10 x + 7 10 y "" = 1 20 x 2 - 3 10 x + 7 10" = 1 10 x - 3 10 = 1 10 (x - 3)
Mēs saņēmām, ka otrais atvasinājums būs 0, ja x ir vienāds ar 0. Tas nozīmē, ka šim punktam nepieciešamais locīšanas nosacījums tiks izpildīts. Tagad mēs izmantojam otro nosacījumu: mēs atrodam trešo atvasinājumu un uzzinām, vai tas kļūs par 0 pie 3:
y " " " = 1 10 (x - 3) " = 1 10
Trešais atvasinājums nepazudīs nevienai x vērtībai. Līdz ar to varam secināt, ka šis punkts būs funkcijas grafika lēciena punkts.
Atbilde: Parādīsim risinājumu attēlā:
Pieņemsim, ka f "(x 0) = 0, f "" (x 0) = 0, . . . , f (n) (x 0) = 0 un f (n + 1) (x 0) ≠ 0 . Šajā gadījumā pāra n gadījumā mēs iegūstam, ka x 0 ir grafika y \u003d f (x) lēciena punkta abscisa.
6. piemērs
Stāvoklis: dota funkcija y = (x - 3) 5 + 1 . Aprēķiniet tā grafika lēciena punktus.
Risinājums
Šī funkcija ir definēta visai reālo skaitļu kopai. Aprēķiniet atvasinājumu: y " = ((x - 3) 5 + 1) " = 5 x - 3 4 . Tā kā tas tiks definēts arī visām argumenta reālajām vērtībām, tad jebkurā tā grafika punktā būs nevertikāla tangensa.
Tagad aprēķināsim, kādām vērtībām otrais atvasinājums kļūs par 0:
y "" = 5 (x - 3) 4 " = 20 x - 3 3 y "" = 0 ⇔ x - 3 = 0 ⇔ x = 3
Mēs esam noskaidrojuši, ka pie x = 3 funkcijas grafikā var būt lēciena punkts. Mēs izmantojam trešo nosacījumu, lai to apstiprinātu:
y " " " = 20 (x - 3) 3 " = 60 x - 3 2, y " " " (3) = 60 3 - 3 2 = 0 y (4) = 60 (x - 3) 2 " = 120 (x - 3) , y (4) (3) = 120 (3 - 3) = 0 y (5) = 120 (x - 3) " = 120, y (5) (3) = 120 ≠ 0
Mums ir n = 4 ar trešo pietiekamo nosacījumu. Tas ir pāra skaitlis, tāpēc x \u003d 3 būs lēciena punkta abscisa, un tam atbilst funkcijas (3; 1) grafika punkts.
Atbilde:Šeit ir šīs funkcijas grafiks ar atzīmētu izliekumu, ieliekumu un lēciena punktu:
Ja pamanāt tekstā kļūdu, lūdzu, iezīmējiet to un nospiediet Ctrl+Enter