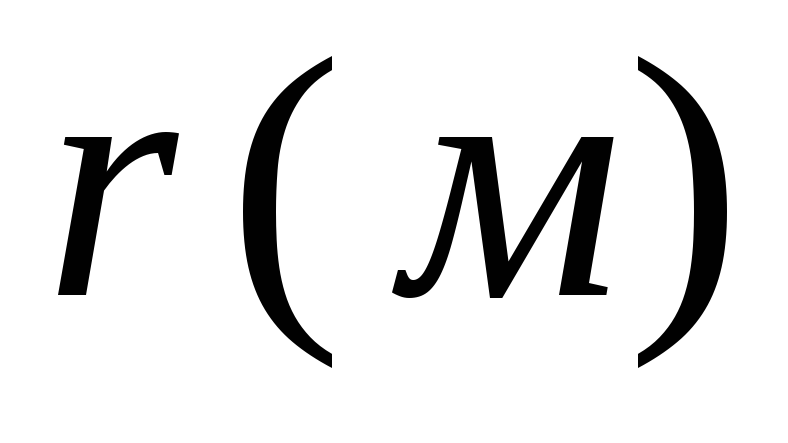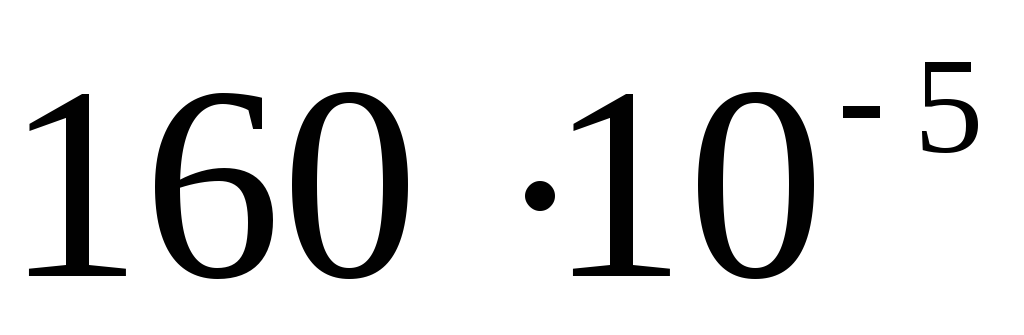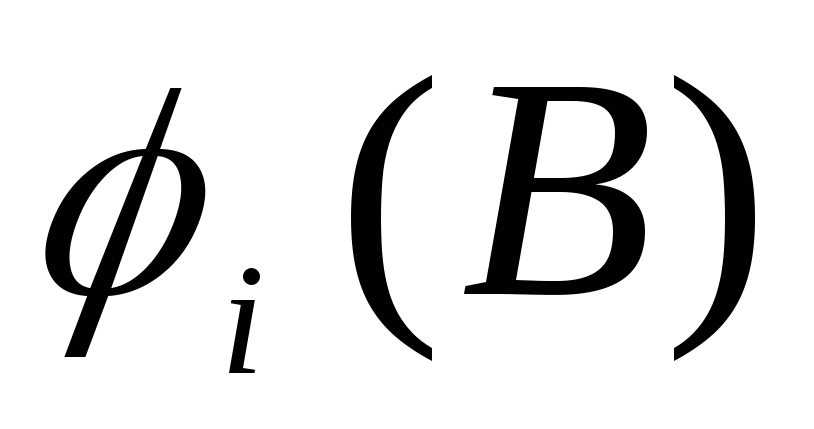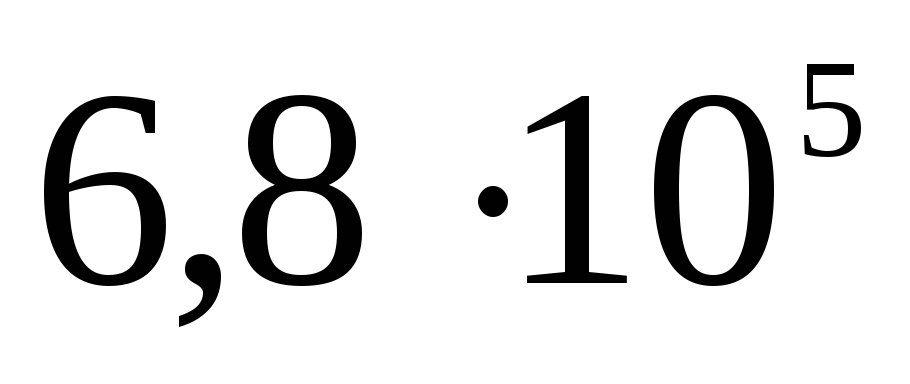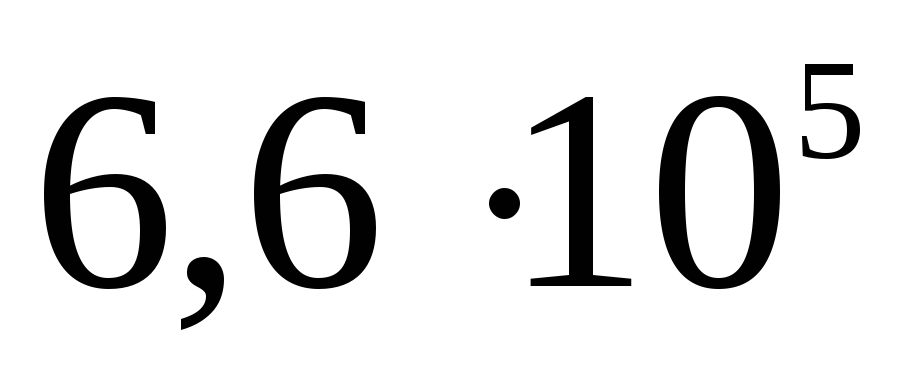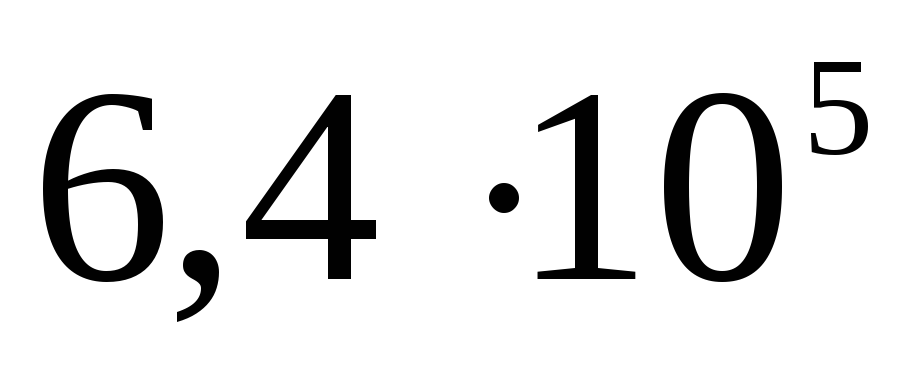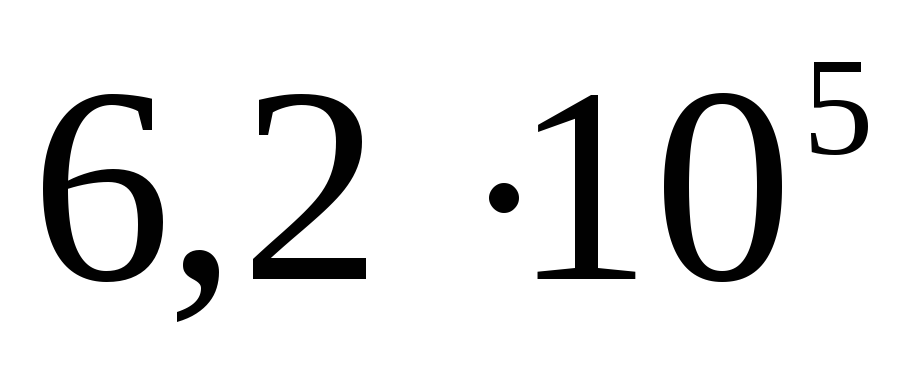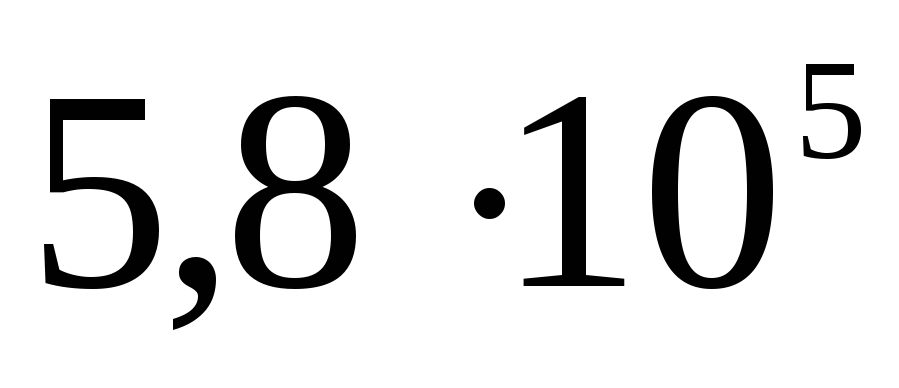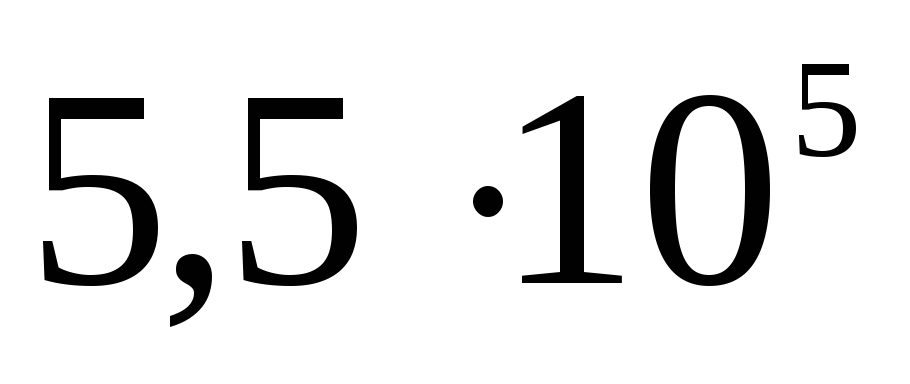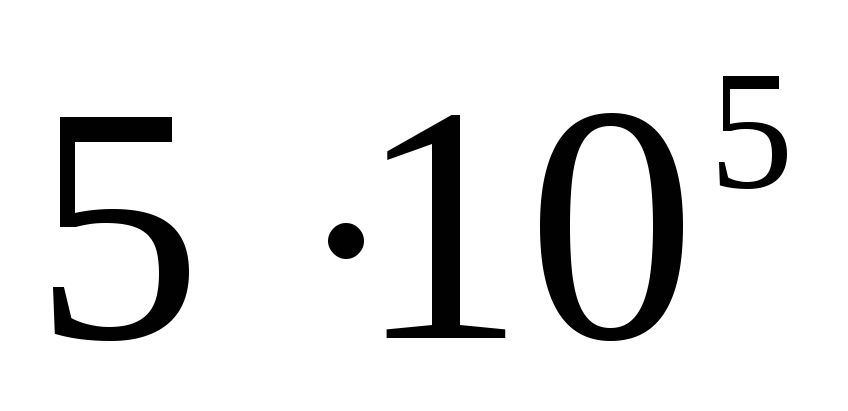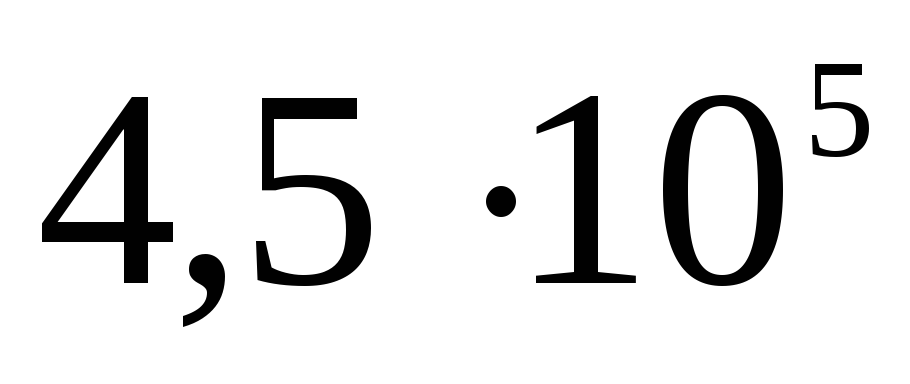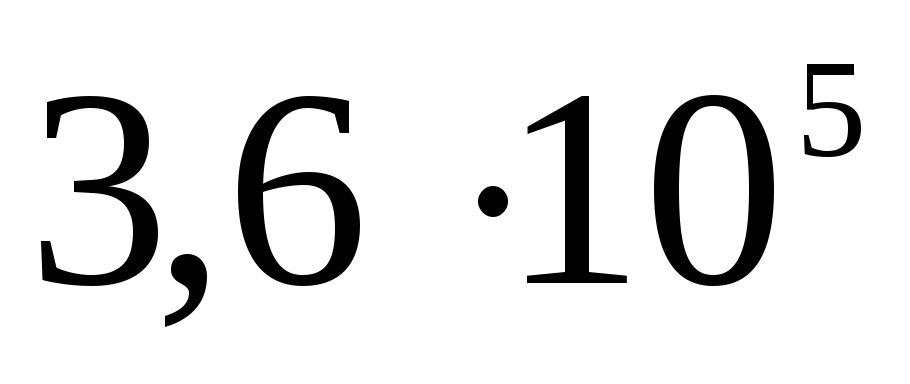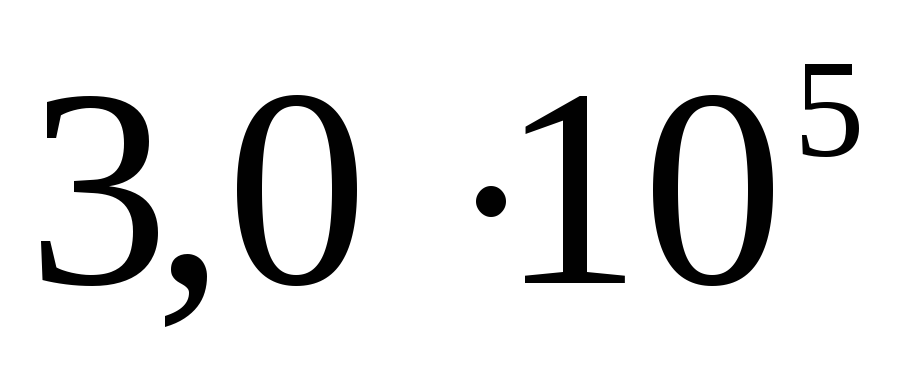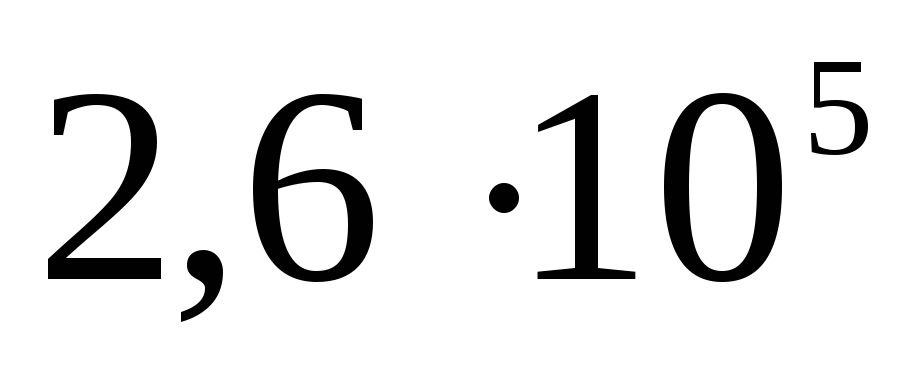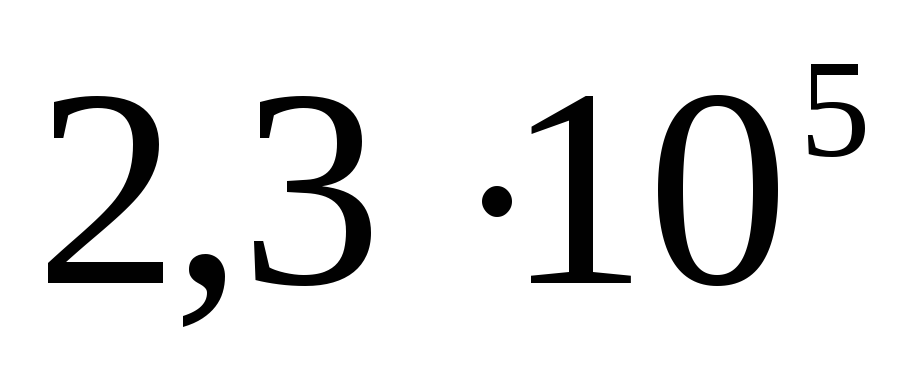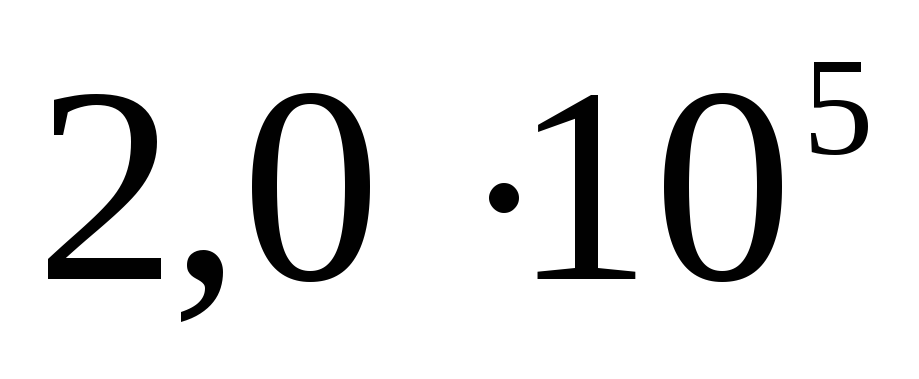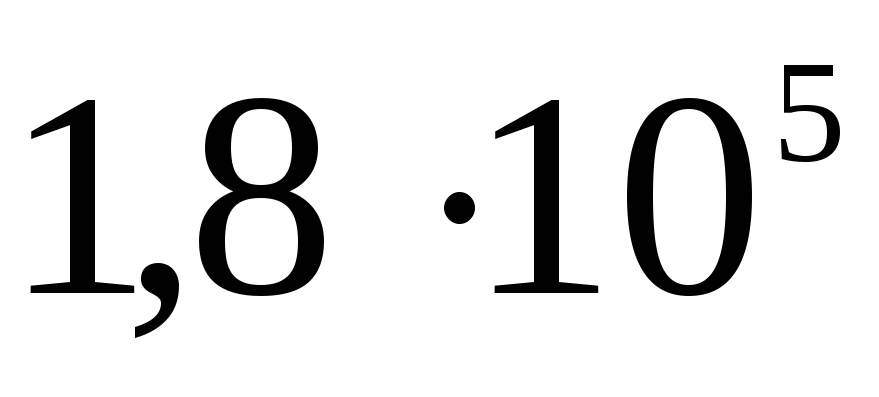ไฟฟ้าสถิต
1
(CT 2001 ทดสอบ 9. A19). รัศมีลูกนำไฟฟ้า R
มีประจุบวก +
q
. ถ้าอยู่ในระยะ2 Rจากศูนย์กลางของลูกบอลวางจุดประจุลบ -2 qแล้วศักยภาพในการเป็นศูนย์กลางของบอล
ข้อผิดพลาดทั่วไปเมื่อแก้มันมาจากการตีความถ้อยคำที่ไม่ถูกต้อง: "ไม่มีสนามในลูกบอลนำ" ข้อสรุปที่ผิดพลาดมาจากข้อความนี้: ทั้งลักษณะของสนาม: ทั้งความเข้มและศักยภาพมีค่าเท่ากับศูนย์ ในกรณีนี้ เฉพาะความแรงของสนามเท่านั้นที่จะเท่ากับศูนย์ เนื่องจาก ประจุอิสระจะหยุดเคลื่อนที่เหนือพื้นผิวตัวนำเมื่อเวกเตอร์  บนพื้นผิวจะตั้งฉากกับจุดใดจุดหนึ่ง พื้นผิวของตัวนำในกรณีนี้มีความเท่าเทียมกัน งานของการเคลื่อนย้ายประจุทดสอบในปริมาตรที่ล้อมรอบด้วยพื้นผิวนั้นเป็นศูนย์เพราะ แรงที่กระทำต่อประจุมีค่าเท่ากับศูนย์ จากนี้ไปพลังงานศักย์ของประจุจะไม่เปลี่ยนแปลงเมื่อเคลื่อนที่จากจุดหนึ่งไปยังอีกจุดหนึ่ง: ศักย์ไฟฟ้าในปริมาตรที่ล้อมรอบด้วยพื้นผิวตัวนำมีค่าคงที่และเท่ากับศักยภาพบนพื้นผิวเอง การเปลี่ยนแปลงของความเข้มและศักย์ของทรงกลมที่มีประจุซึ่งมีระยะห่างจากจุดศูนย์กลางของประจุสามารถแสดงเป็นกราฟได้ (ดูรูปที่)
บนพื้นผิวจะตั้งฉากกับจุดใดจุดหนึ่ง พื้นผิวของตัวนำในกรณีนี้มีความเท่าเทียมกัน งานของการเคลื่อนย้ายประจุทดสอบในปริมาตรที่ล้อมรอบด้วยพื้นผิวนั้นเป็นศูนย์เพราะ แรงที่กระทำต่อประจุมีค่าเท่ากับศูนย์ จากนี้ไปพลังงานศักย์ของประจุจะไม่เปลี่ยนแปลงเมื่อเคลื่อนที่จากจุดหนึ่งไปยังอีกจุดหนึ่ง: ศักย์ไฟฟ้าในปริมาตรที่ล้อมรอบด้วยพื้นผิวตัวนำมีค่าคงที่และเท่ากับศักยภาพบนพื้นผิวเอง การเปลี่ยนแปลงของความเข้มและศักย์ของทรงกลมที่มีประจุซึ่งมีระยะห่างจากจุดศูนย์กลางของประจุสามารถแสดงเป็นกราฟได้ (ดูรูปที่)
วิธีการแก้
ศักยภาพที่เกิดจากประจุแบบกระจายแบบสมมาตรทรงกลม qอยู่ตรงกลางของลูกบอลเหมือนกับบนพื้นผิวและเท่ากับ φ 1 = q/4 πε 0 R; ศักยภาพที่สร้างขึ้นที่จุดเดียวกันโดยประจุจุด -2 q อยู่นอกทรงกลมในระยะ 2 R จากศูนย์กลางคือ φ 2 = – 2 q/4 πε 0 2 R; ศักยภาพที่ศูนย์กลางของลูกบอลเป็นผลมาจากการซ้อนทับของสองสนามคือ φ = φ 1 + φ 2 = q/4 πε 0 R–2 q/4 πε 0 2 R= 0 .
ขณะทำ งานทดสอบสะดวกในการเก็บรายการให้สั้นที่สุด ตัวอย่างเช่น ในกรณีนี้ สมการทั่วไปหนึ่งสมการก็เพียงพอแล้ว φ = q/4 πε 0 r.
เพราะ ประจุลบเป็นจุดเป็นสองเท่าของประจุที่กระจายบนทรงกลมและอยู่ห่างจากศูนย์กลางของทรงกลมเป็นสองเท่า จะเห็นได้จากสมการที่เขียนว่าศักย์ของประจุทั้งสองมีขนาดเท่ากันและมีเครื่องหมายตรงข้ามกัน ดังนั้น ศักยภาพที่ได้คือ 0
2 (CT 2001 ทดสอบ 11 A 19).
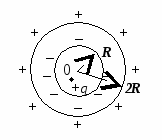 ภายในชั้นโลหะทรงกลมรัศมีด้านในและด้านนอกมีค่าเท่ากัน R
และ 2
R
,
ระยะทาง อาร์/
2
q
.
ศักยภาพที่จุดศูนย์กลางของทรงกลมคือ...
ภายในชั้นโลหะทรงกลมรัศมีด้านในและด้านนอกมีค่าเท่ากัน R
และ 2
R
,
ระยะทาง อาร์/
2
q
.
ศักยภาพที่จุดศูนย์กลางของทรงกลมคือ...
วิธีการแก้
ความยากลำบากทำให้เกิดการสร้างภาพการกระจายประจุบนพื้นผิวของชั้นทรงกลม
เนื่องจากการเหนี่ยวนำไฟฟ้าสถิต ประจุจึงปรากฏบนพื้นผิวด้านในของทรงกลม –
q
, และด้านนอก + q
.
ศักยภาพที่จุดศูนย์กลางของทรงกลม 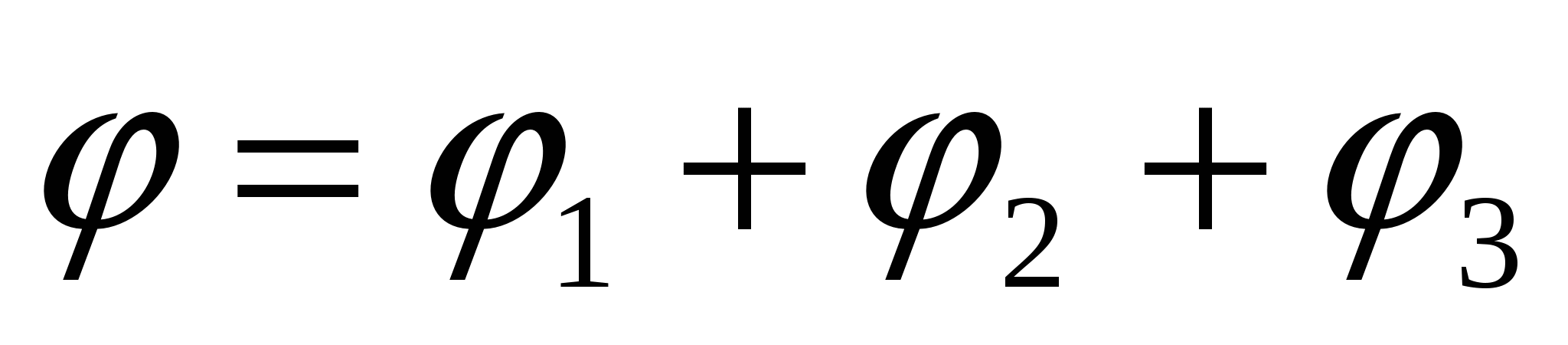 ;
;
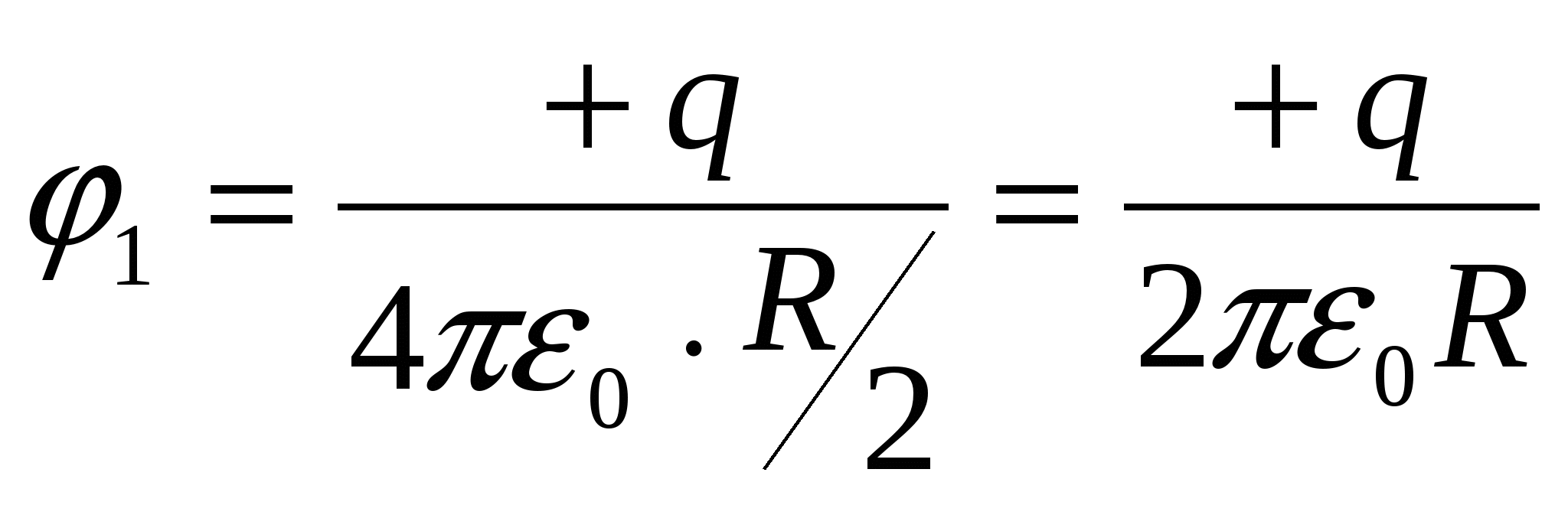 ;
; 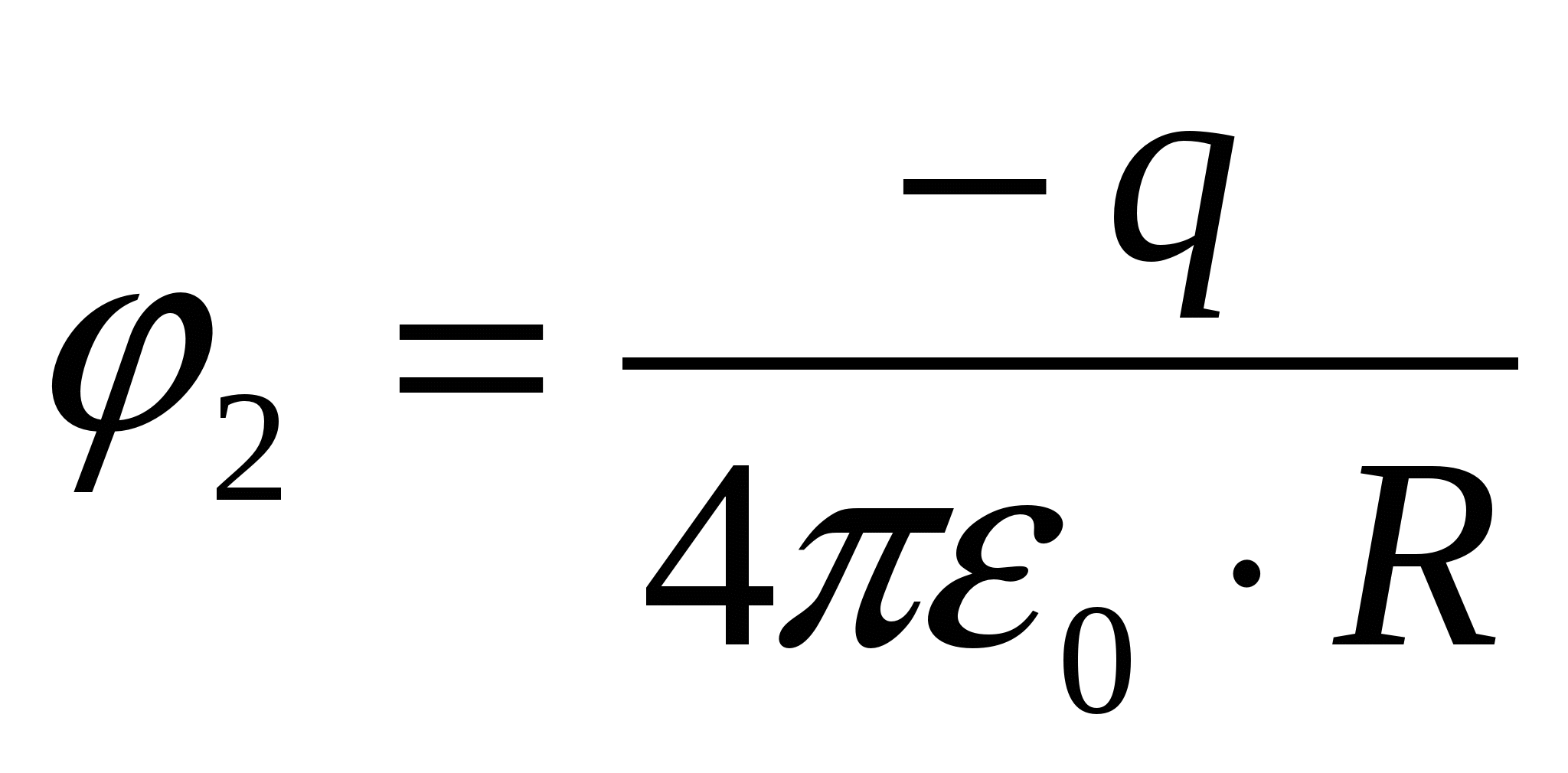 ;
; 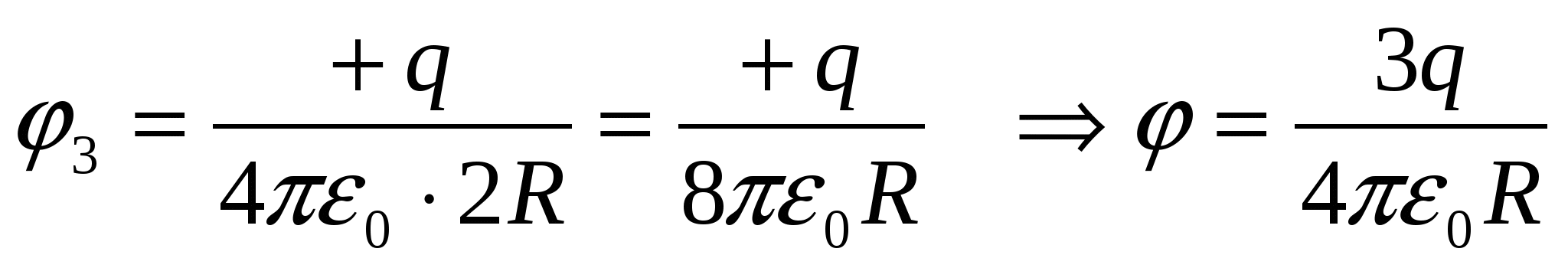 – คำตอบ 1
– คำตอบ 1
งานที่คล้ายกัน - A 19 ในการทดสอบครั้งที่ 12, 2001 :
ภายในชั้นโลหะทรงกลม รัศมีด้านในและด้านนอกมีค่าเท่ากับ 2 . ตามลำดับ R และ 4 R , ระยะทาง R มีประจุบวกจากจุดศูนย์กลาง q . ศักยภาพที่จุดศูนย์กลางของทรงกลมคือ ….
ตอบ: 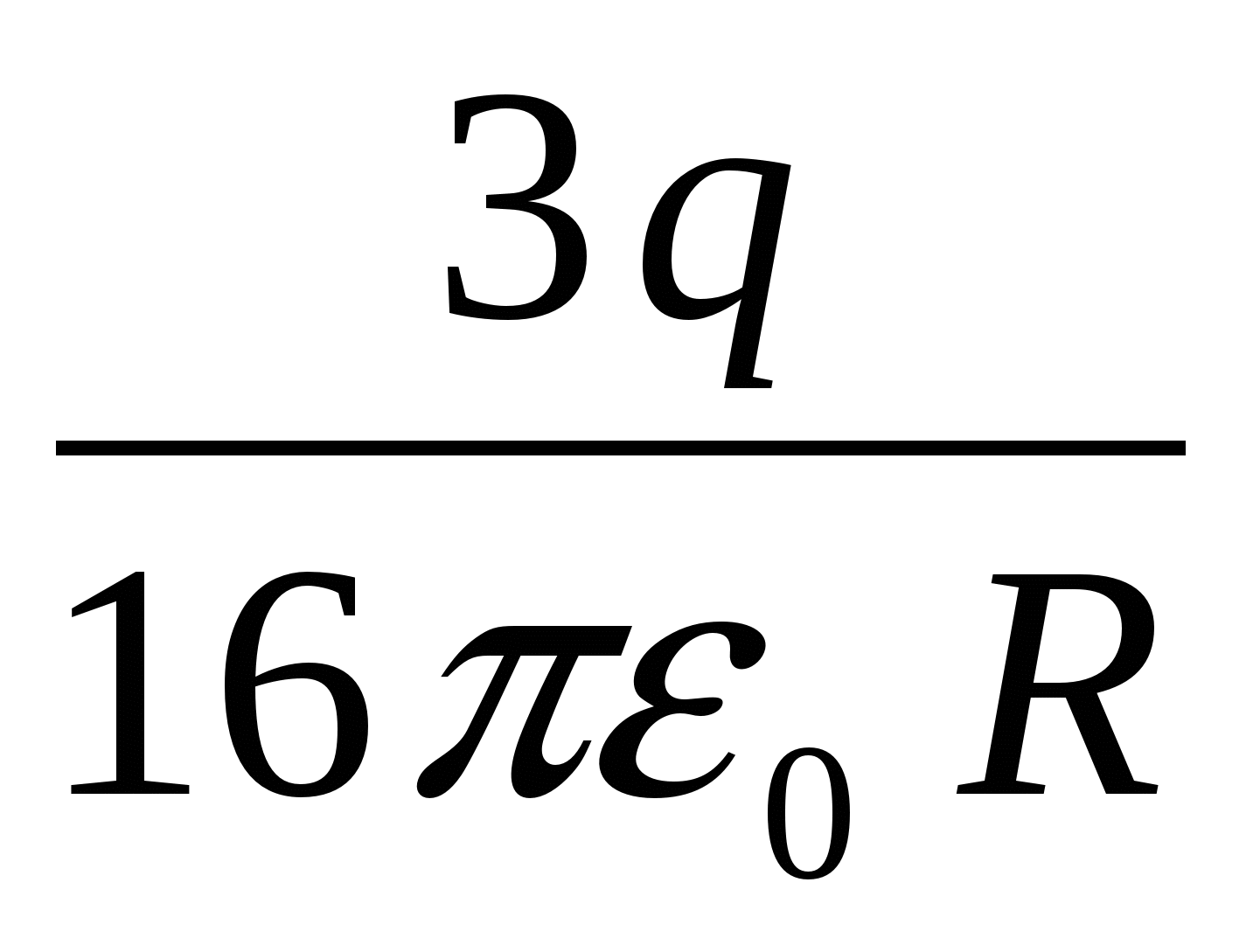
3 (CT 2000 ทดสอบ ... A19). ลูกเหล็กมีรัศมี R 1 มีศักยภาพ φ 1 ล้อมรอบด้วยเปลือกตัวนำทรงกลมที่ไม่มีประจุซึ่งมีรัศมี R 2 . ค้นหาศักยภาพของลูกบอลหลังจากเชื่อมต่อกับเปลือกไประยะหนึ่งหรือไม่?
วิธีการแก้
ศักยภาพของบอลพุ่ง 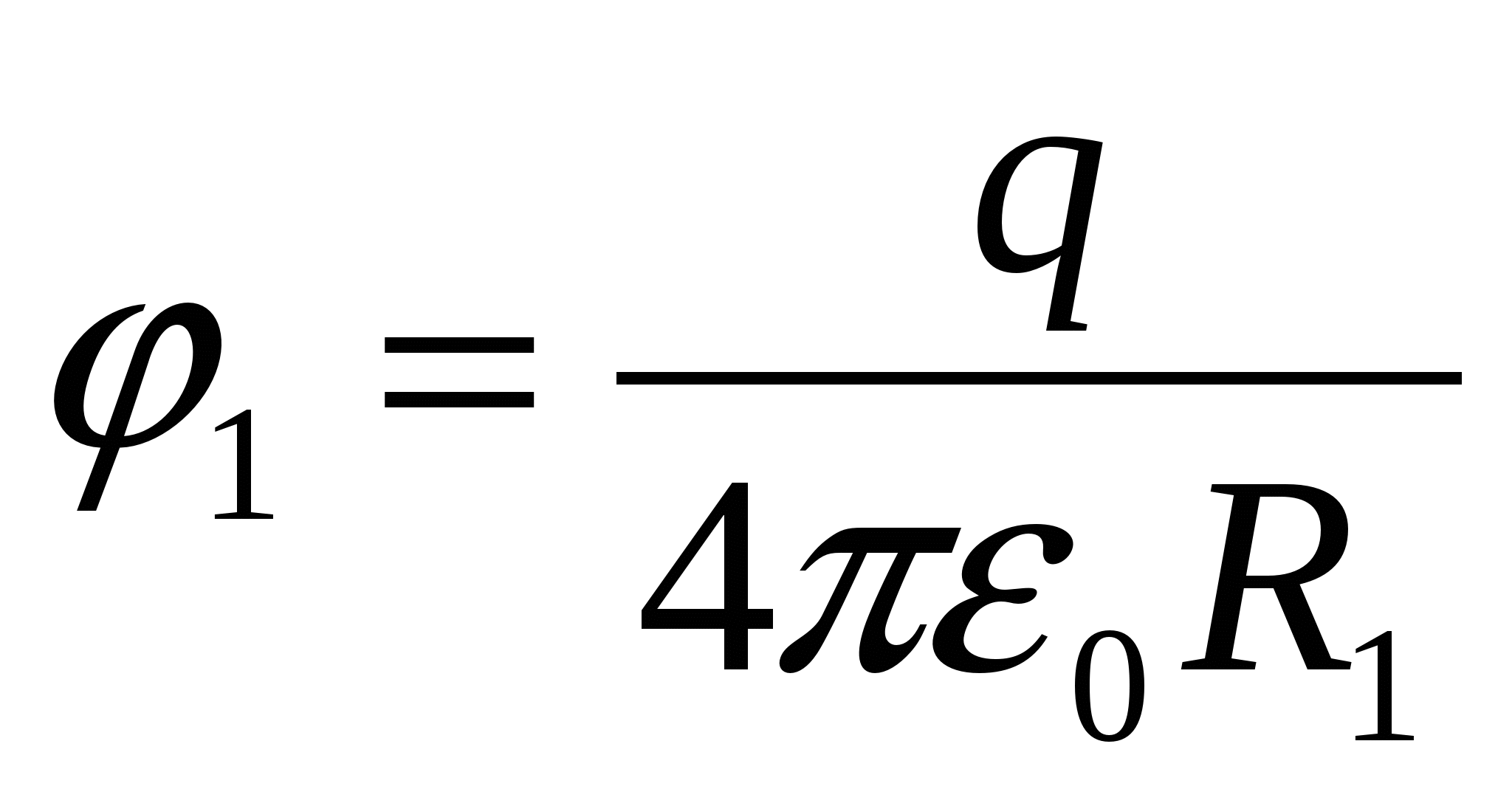 .
.
ถ้าลูกบอลที่ถูกชาร์จไปสัมผัสพื้นผิวด้านในของเปลือก ประจุ พยายามที่จะปักหลักบนความเป็นไปได้ ระยะทางไกลจากกันไปที่เปลือก ความแรงของสนามภายในเปลือกจะเท่ากับ 0 ศักย์สนามที่จุดของเปลือกและภายในจะเท่ากับ 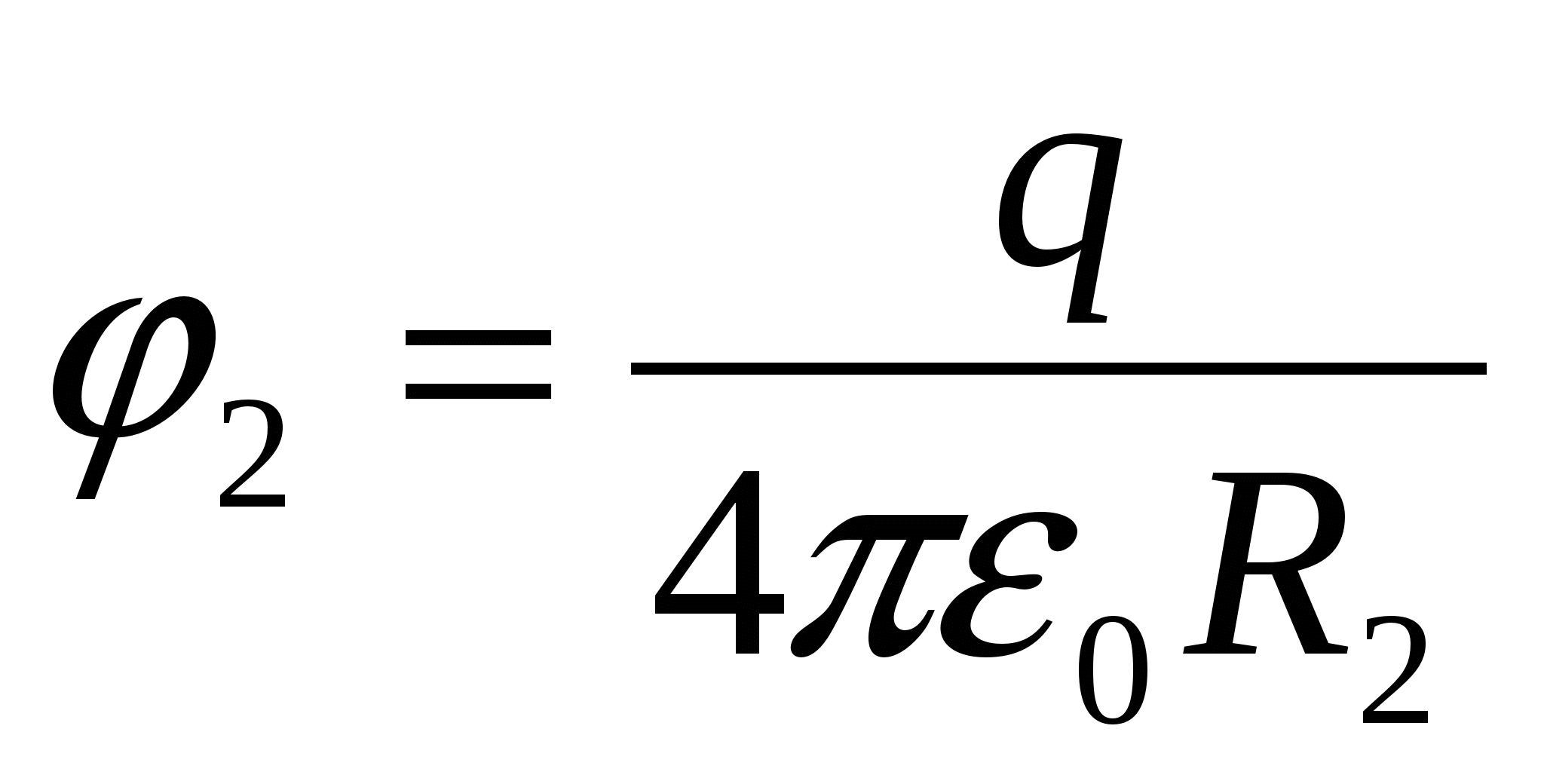 (แต่ไม่ใช่ 0!ดูปัญหาก่อนหน้า) โดยที่
(แต่ไม่ใช่ 0!ดูปัญหาก่อนหน้า) โดยที่  . ดังนั้นศักยภาพของเปลือกและลูกที่อยู่ข้างในและเชื่อมต่อกับมันมีค่าเท่ากับ
. ดังนั้นศักยภาพของเปลือกและลูกที่อยู่ข้างในและเชื่อมต่อกับมันมีค่าเท่ากับ 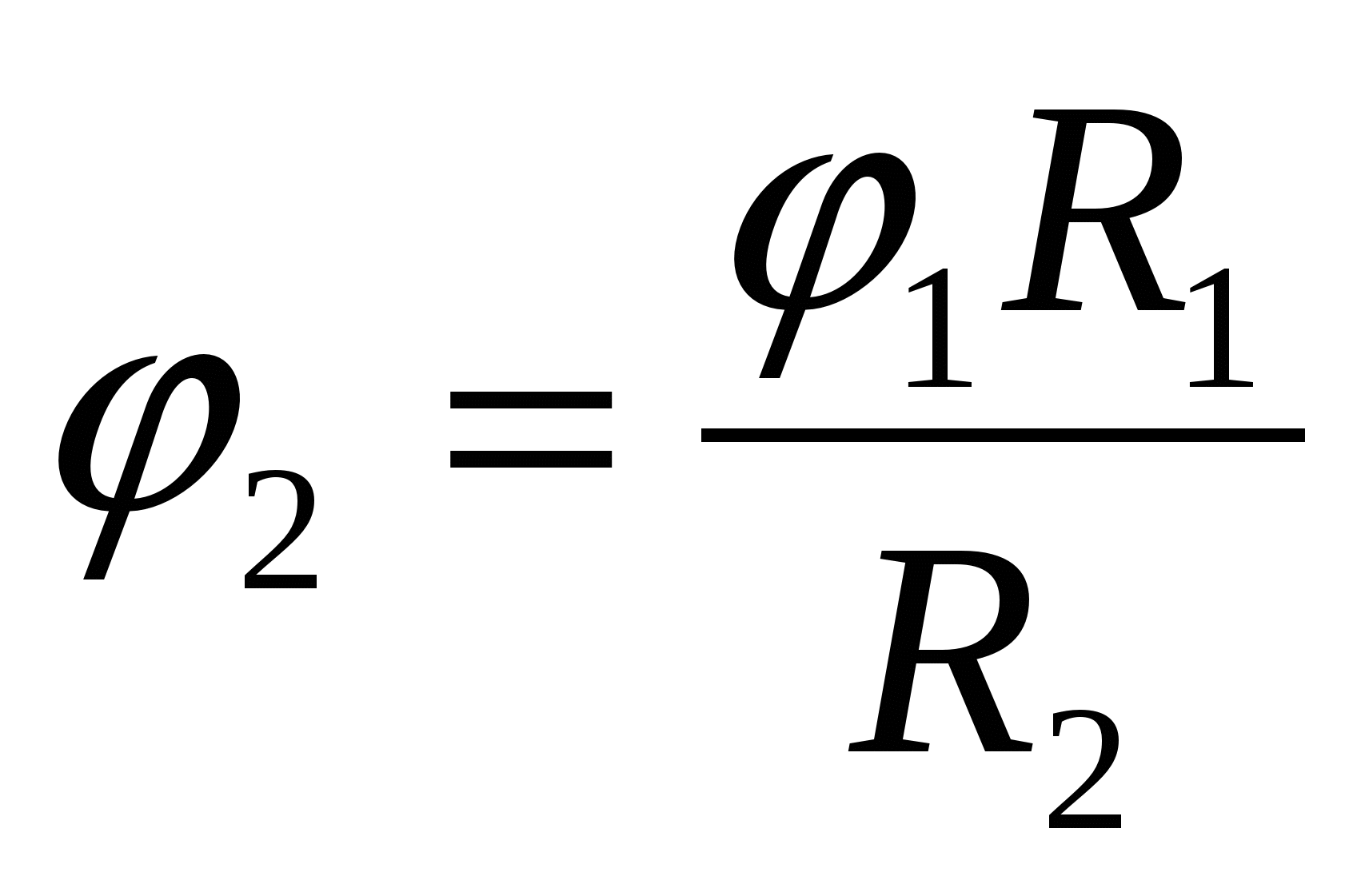 – คำตอบ.
– คำตอบ.
ถูกต้อง คำตอบ -1.
4 (CT 2000 ทดสอบ ... A19). รัศมีลูกโลหะ R 1 มีศักยภาพ φ 1 ล้อมรอบด้วยเปลือกทรงกลมนำไฟฟ้ารัศมี R 2 . ศักยภาพของลูกบอลจะเป็นอย่างไรถ้าเปลือกถูกต่อสายดิน?
วิธีการแก้
ที่พบมากที่สุด ข้อผิดพลาดคือไม่คำนึงถึงศักยภาพของสนามที่เกิดจากประจุที่เหนี่ยวนำให้เกิดบนเปลือกเมื่อต่อสายดิน
ตัวเลือกแรก โซลูชั่น. ศักยภาพบนพื้นผิวของลูกบอลที่เกิดจากการพุ่งเข้าของลูกบอล 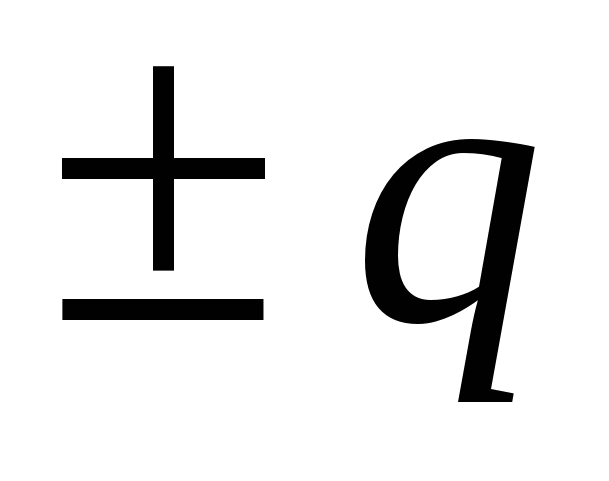 , เท่ากับ
, เท่ากับ 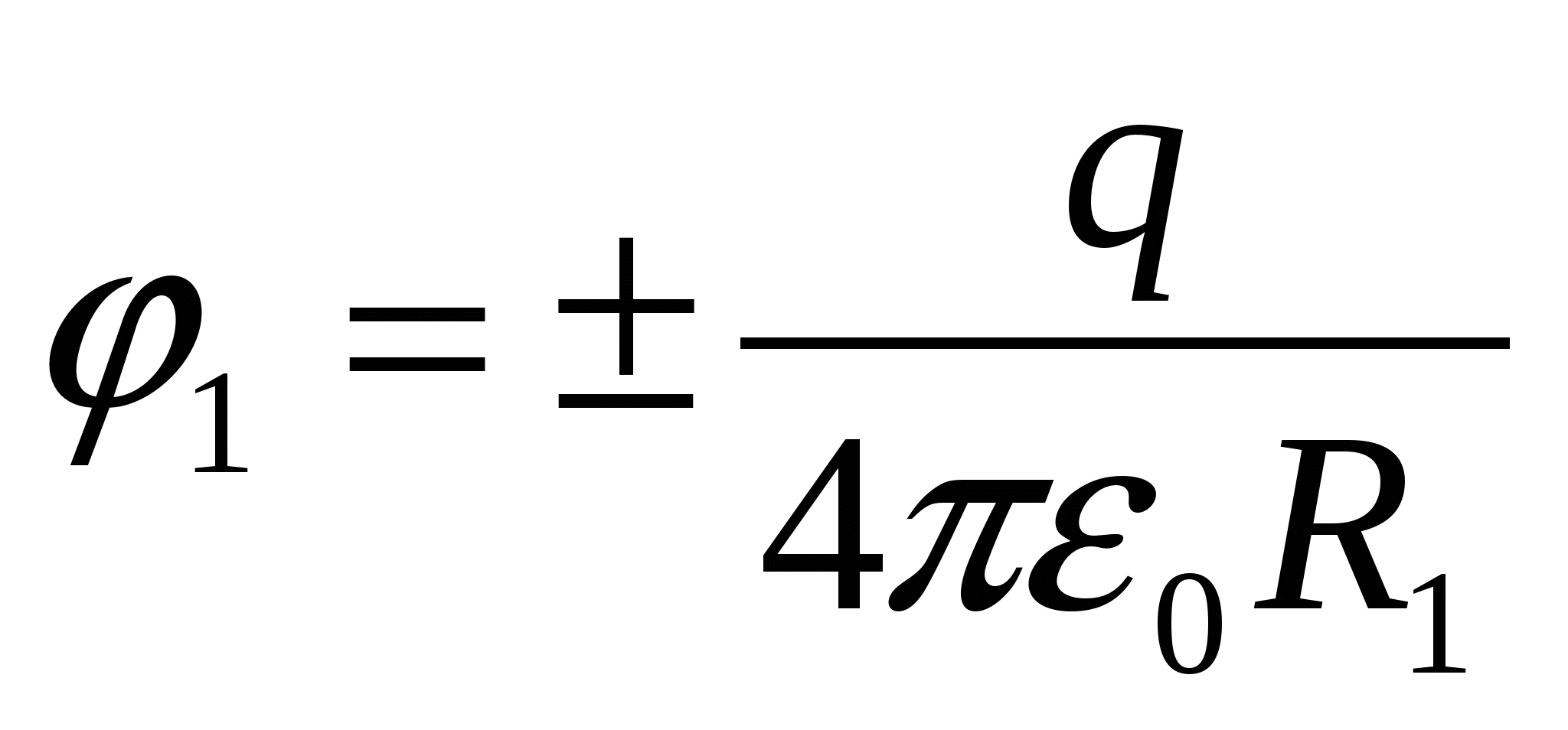 . หลังจากที่เปลือกถูกต่อสายดิน ประจุเหนี่ยวนำจะปรากฏขึ้น
. หลังจากที่เปลือกถูกต่อสายดิน ประจุเหนี่ยวนำจะปรากฏขึ้น 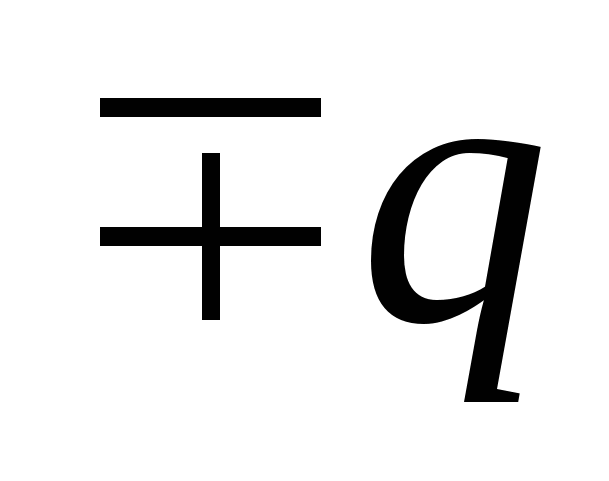 ซึ่งทั้งเปลือกและภายในสร้างศักยภาพ
ซึ่งทั้งเปลือกและภายในสร้างศักยภาพ 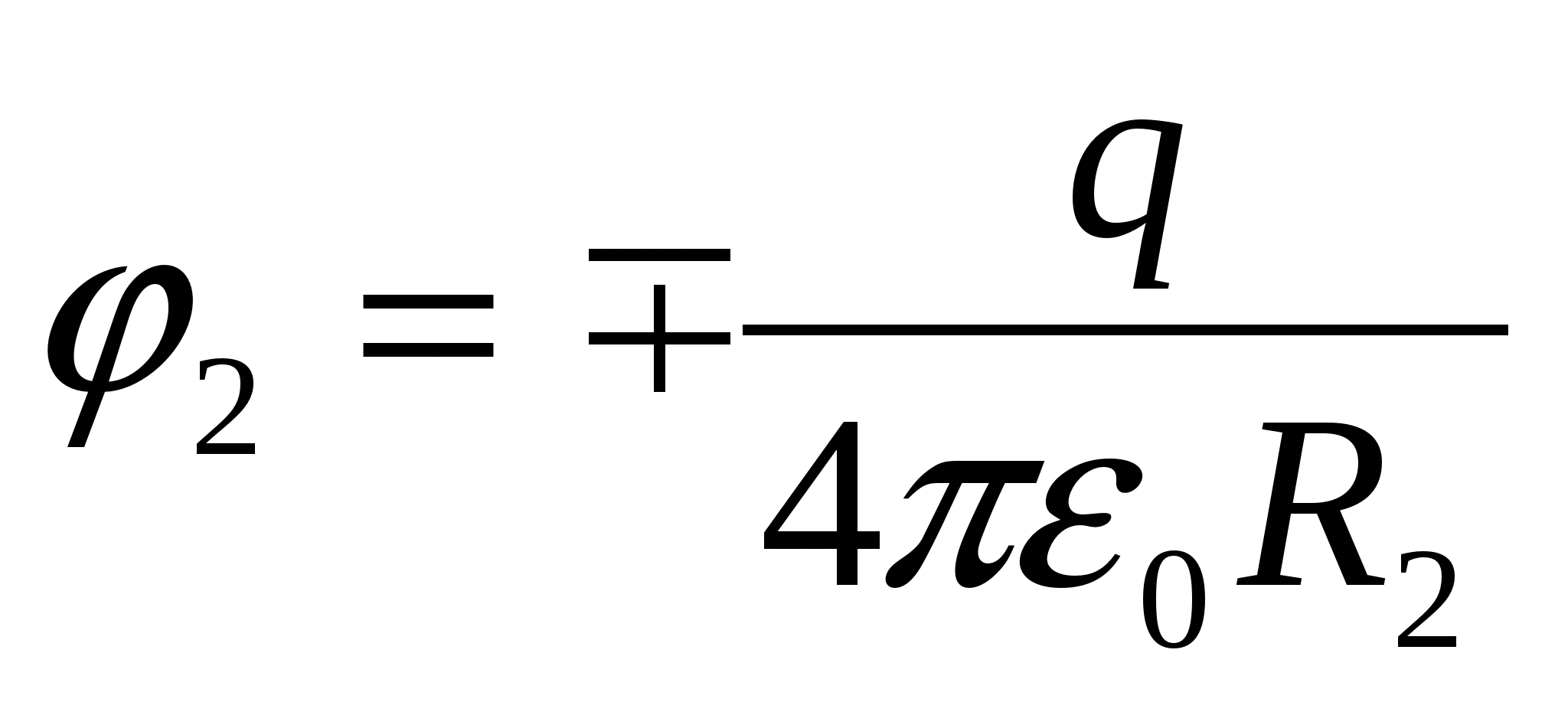 .
.
การซ้อนทับของสนามเริ่มต้นของลูกบอลและสนามที่เกิดจากประจุเหนี่ยวนำของเปลือกทำให้เกิดศักยภาพบนพื้นผิวของลูกบอล
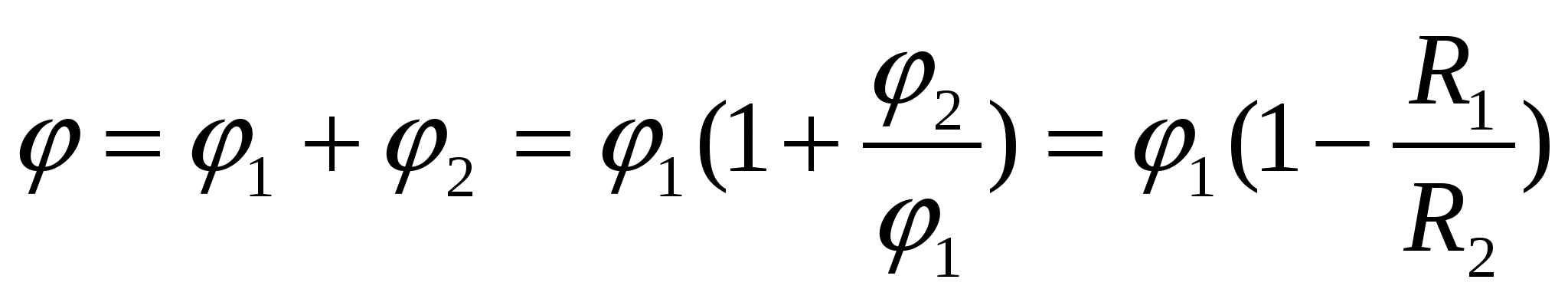 – คำตอบ.
– คำตอบ.
ตัวเลือกที่สอง โซลูชั่น. จะเถียงว่า ศักยภาพของเปลือกหลังจากต่อสายดินคือ 0,ตามธรรมเนียมในเทคโนโลยี (ใช้ปลอกหุ้มเป็นจุดอ้างอิงสำหรับพลังงานศักย์) จากเงื่อนไขนี้ จะพบขนาดและเครื่องหมายของประจุเหนี่ยวนำ ศักยภาพของเชลล์ φ 2 คือผลรวมของศักย์ไฟฟ้าที่เกิดจากประจุที่เกิดขึ้น q 2 และศักยภาพของสนามบอล φ 1 :
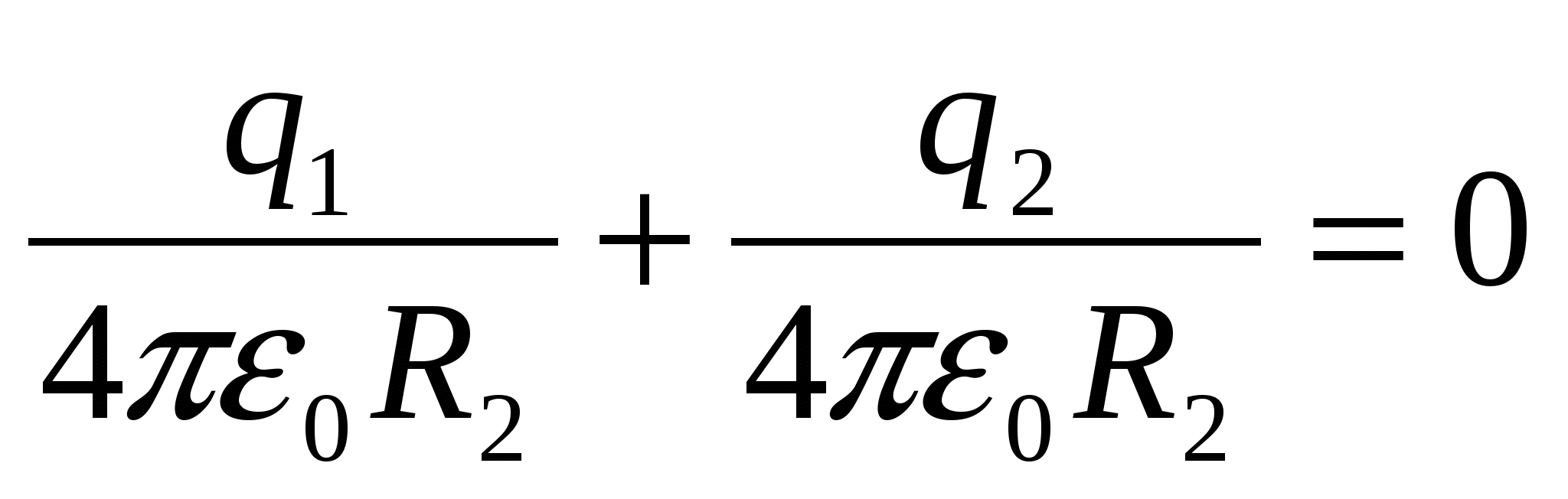 ,
,  q 1
= –
q 2.
.
q 1
= –
q 2.
.
เราพบศักยภาพของลูกบอลหลังจากที่เปลือกถูกลงดิน:
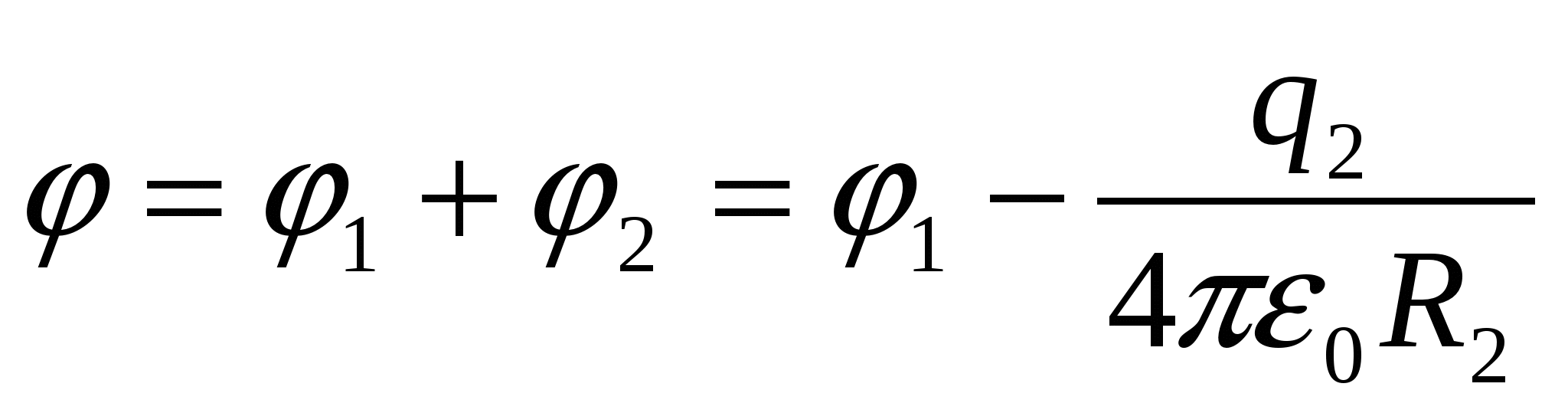 (1).
(1).
จาก 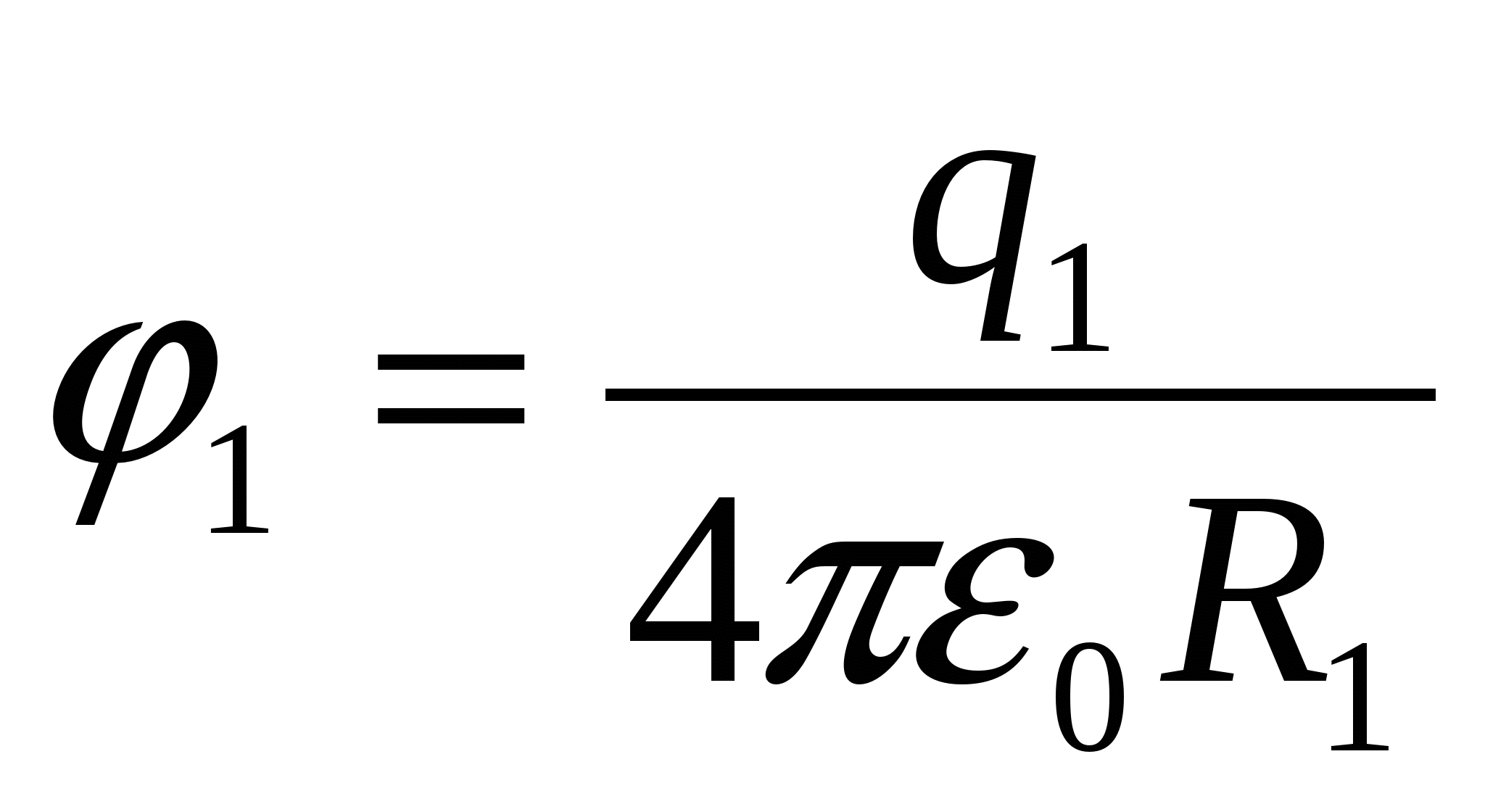 หา
หา 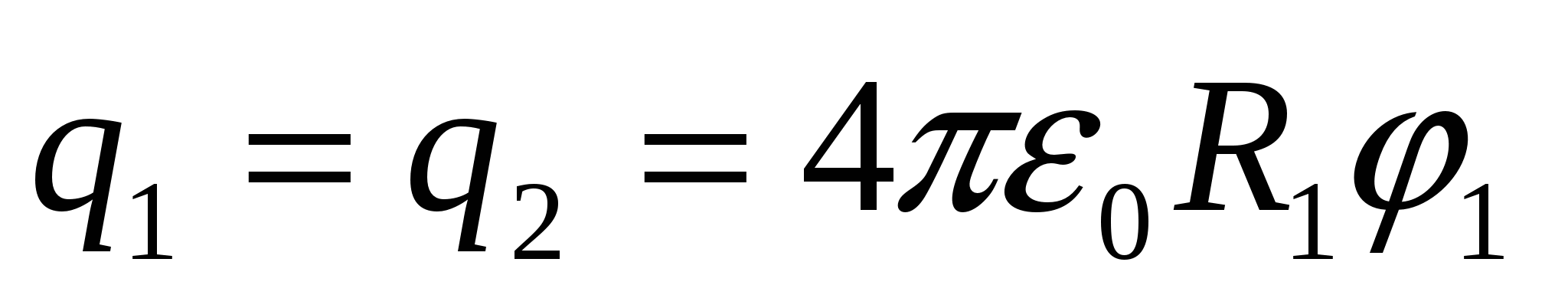 , เราแทน (1), เราได้ คำตอบ:
, เราแทน (1), เราได้ คำตอบ: 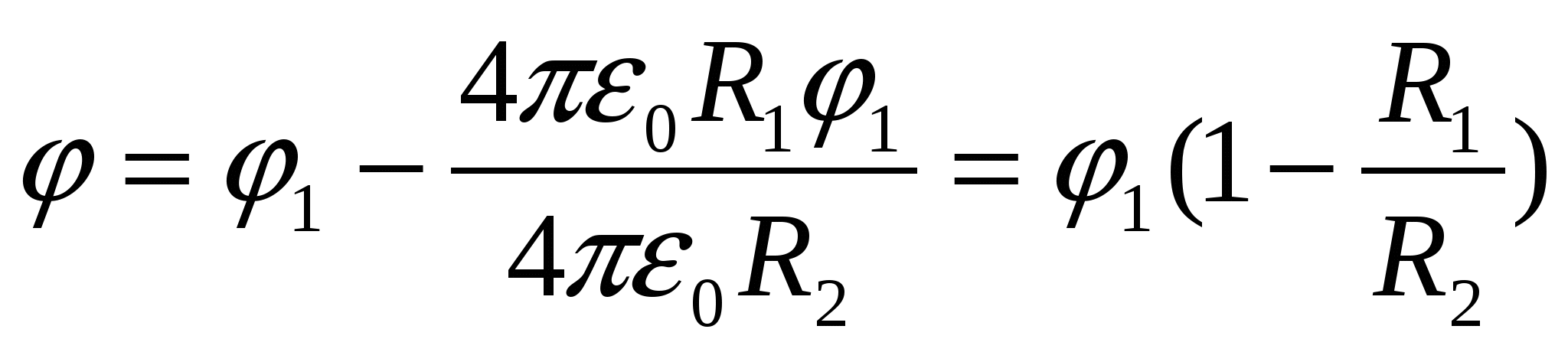 .
.
โซลูชันนี้มีข้อเสียบางประการ:
– ในปัญหาที่แก้ไขก่อนหน้านี้ ศักย์ (พลังงานศักย์) ถูกนับจากจุดที่ห่างไกลจากประจุอย่างไม่สิ้นสุด ซึ่งมีความหมายทางกายภาพที่ชัดเจน มีเหตุผลที่จะใช้จุดอ้างอิงเดียวกันเสมอ
- การแก้ปัญหากลายเป็นเรื่องยุ่งยากมากขึ้น
5
(CT 2001 ทดสอบ 3. A19). วงแหวนรัศมีคงที่บาง Rชาร์จสม่ำเสมอเพื่อให้มีประจุต่อความยาวของวงแหวน + γ .
ในสุญญากาศบนแกนของวงแหวนในระยะไกล lจากศูนย์กลางวางลูกบอลขนาดเล็กที่มีประจุ + q. หากปล่อยลูกบอล ในกระบวนการเคลื่อนที่ ลูกบอลจะได้รับพลังงานจลน์สูงสุดเท่ากับ
| 1) 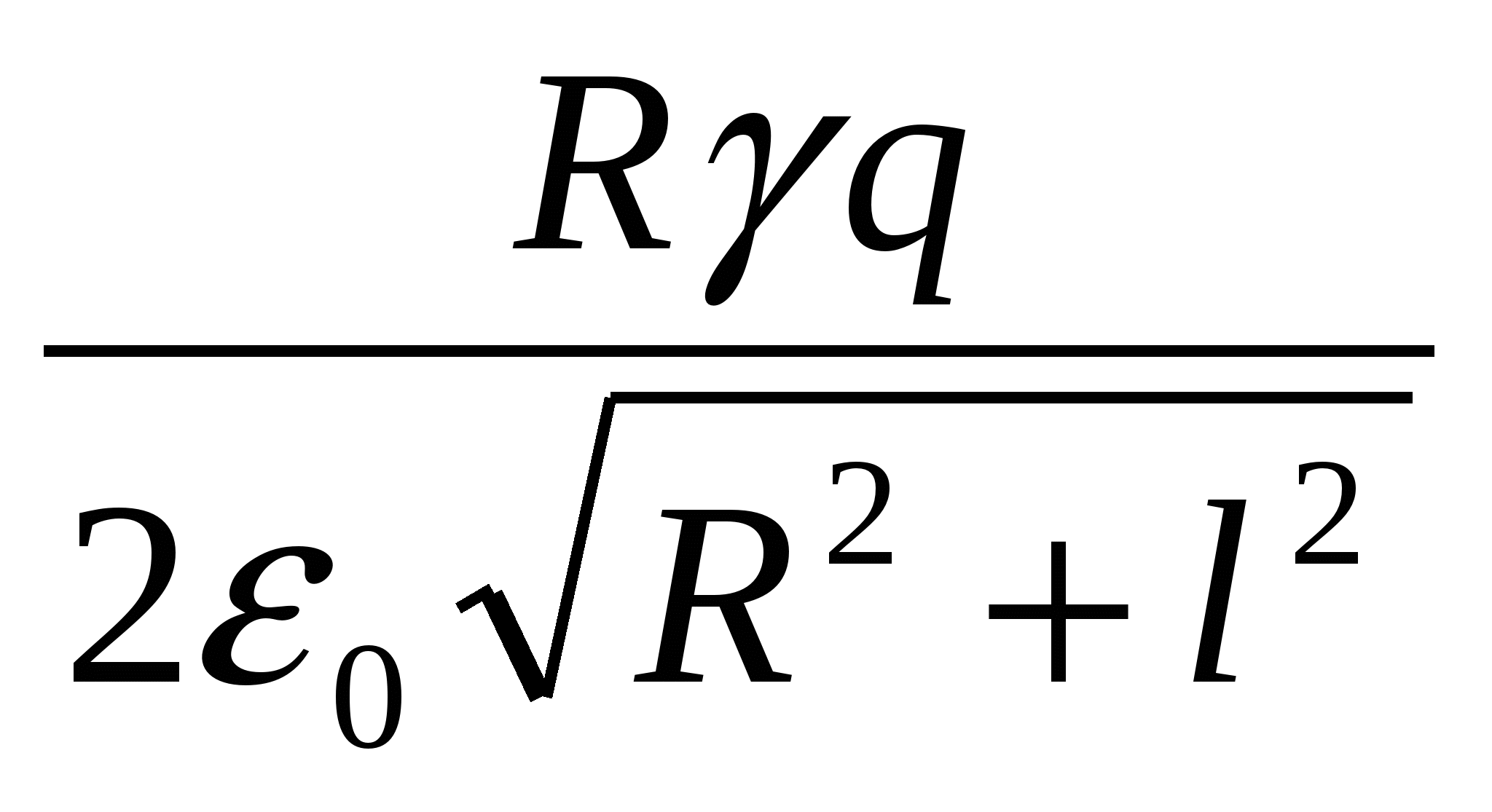 | 2) 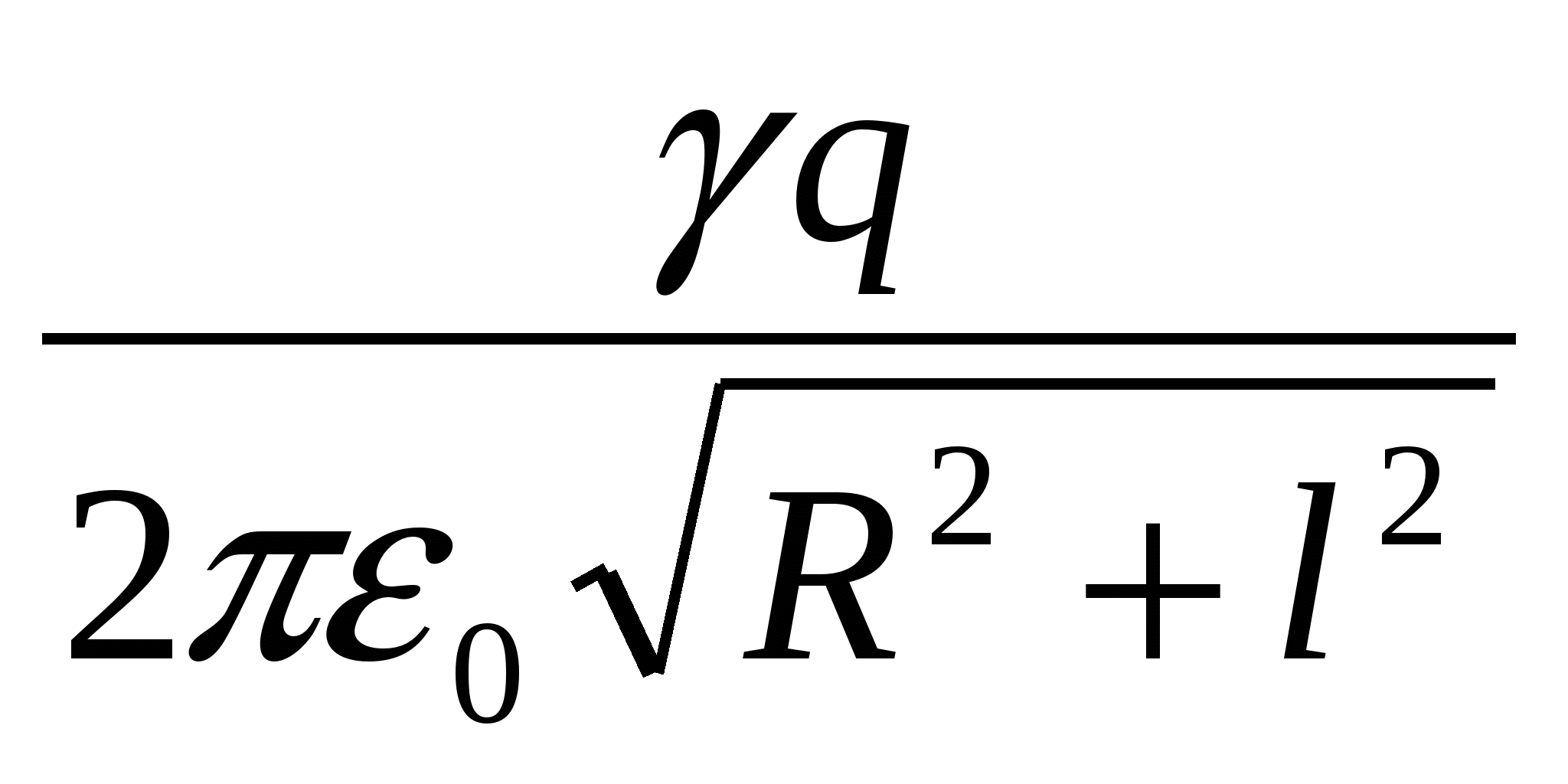 | 3) 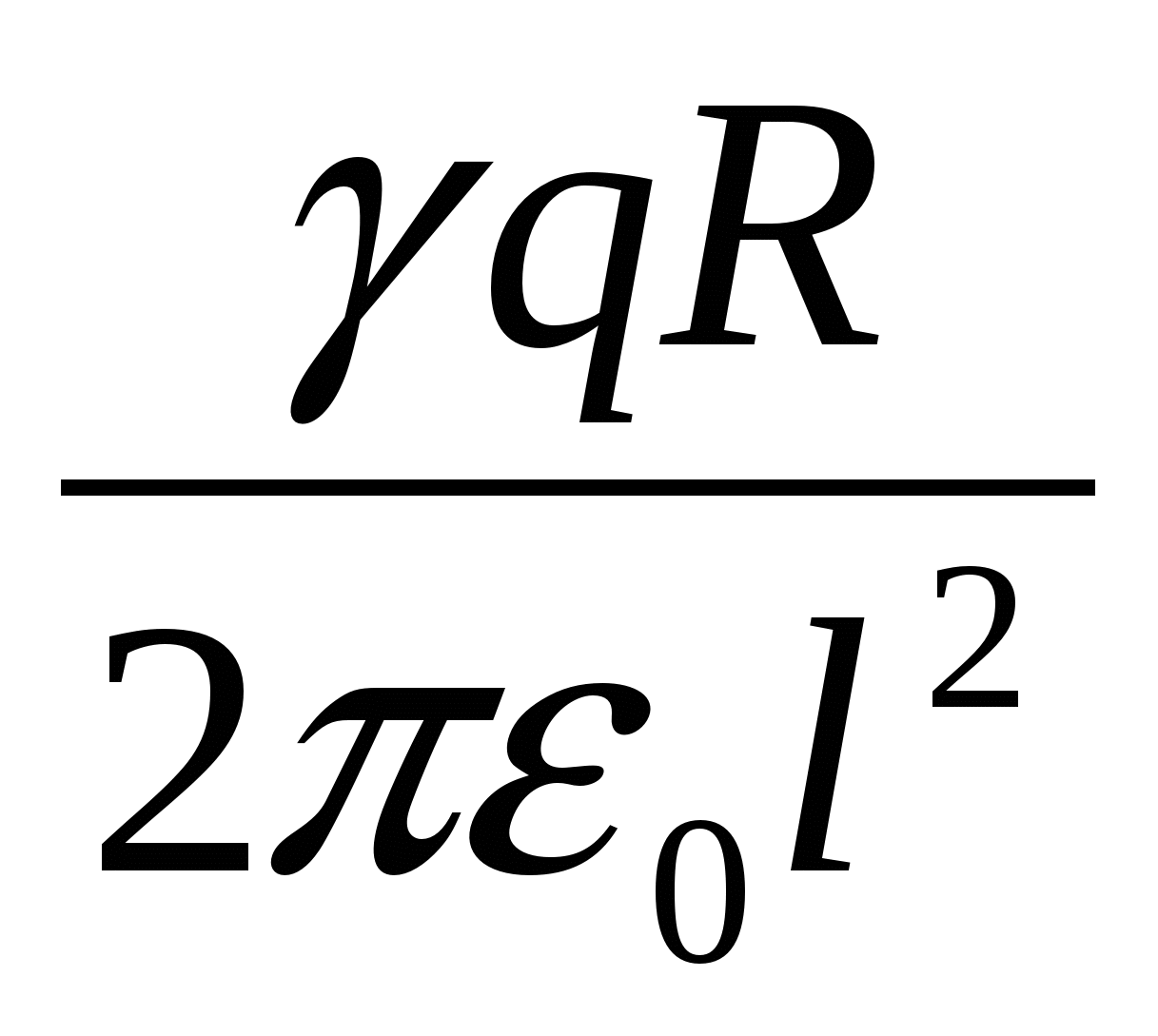 |
| 4) 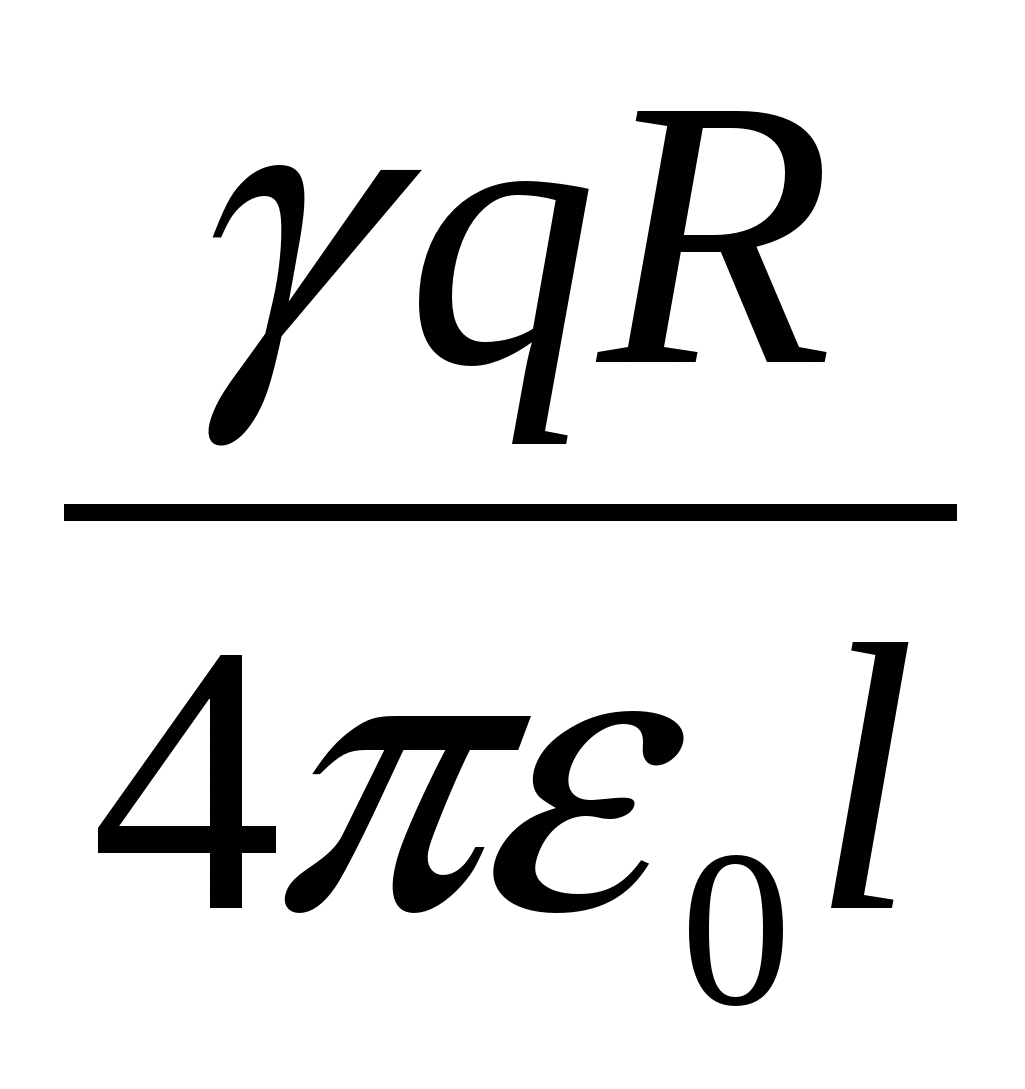 | 5) 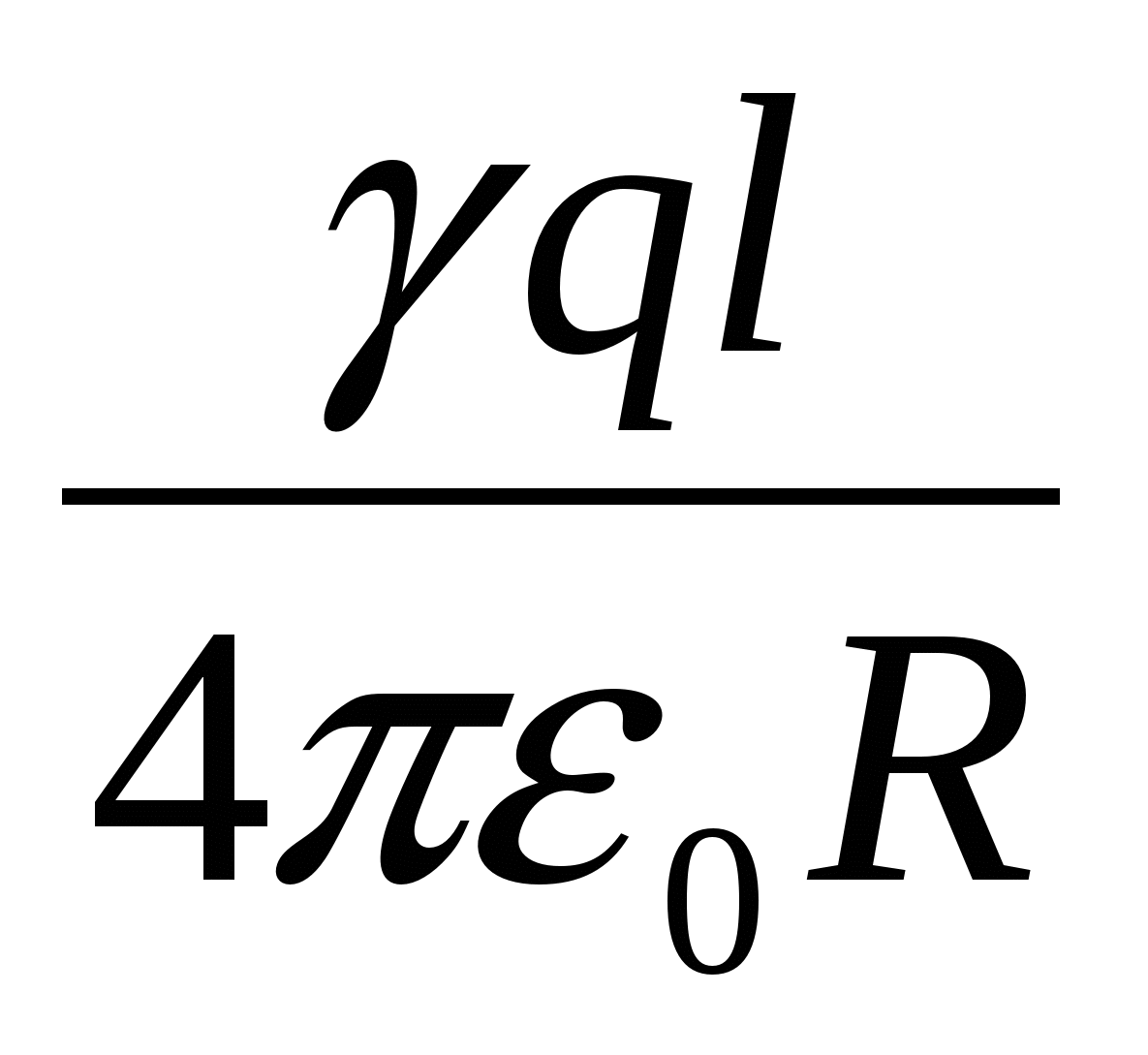 |
R 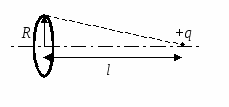 วิธีการแก้
วิธีการแก้
ตามกฎการอนุรักษ์พลังงาน อี = ยู, ที่ไหน ยู- พลังงานปฏิสัมพันธ์ ค่าจุดและแหวน
ข้อผิดพลาดทั่วไป:ในการแก้ปัญหานี้ ถือว่า เนื่องจากความสมมาตรของการกระจายประจุไปตามวงแหวนจึงเป็นไปได้ที่จะ “ดึง” ไปที่ศูนย์กลางของวงแหวนและค้นหาศักยภาพของสนามที่สร้างขึ้นโดยวงแหวนที่ตำแหน่ง ของประจุ ตามศักยภาพของสนามของประจุแบบจุด: 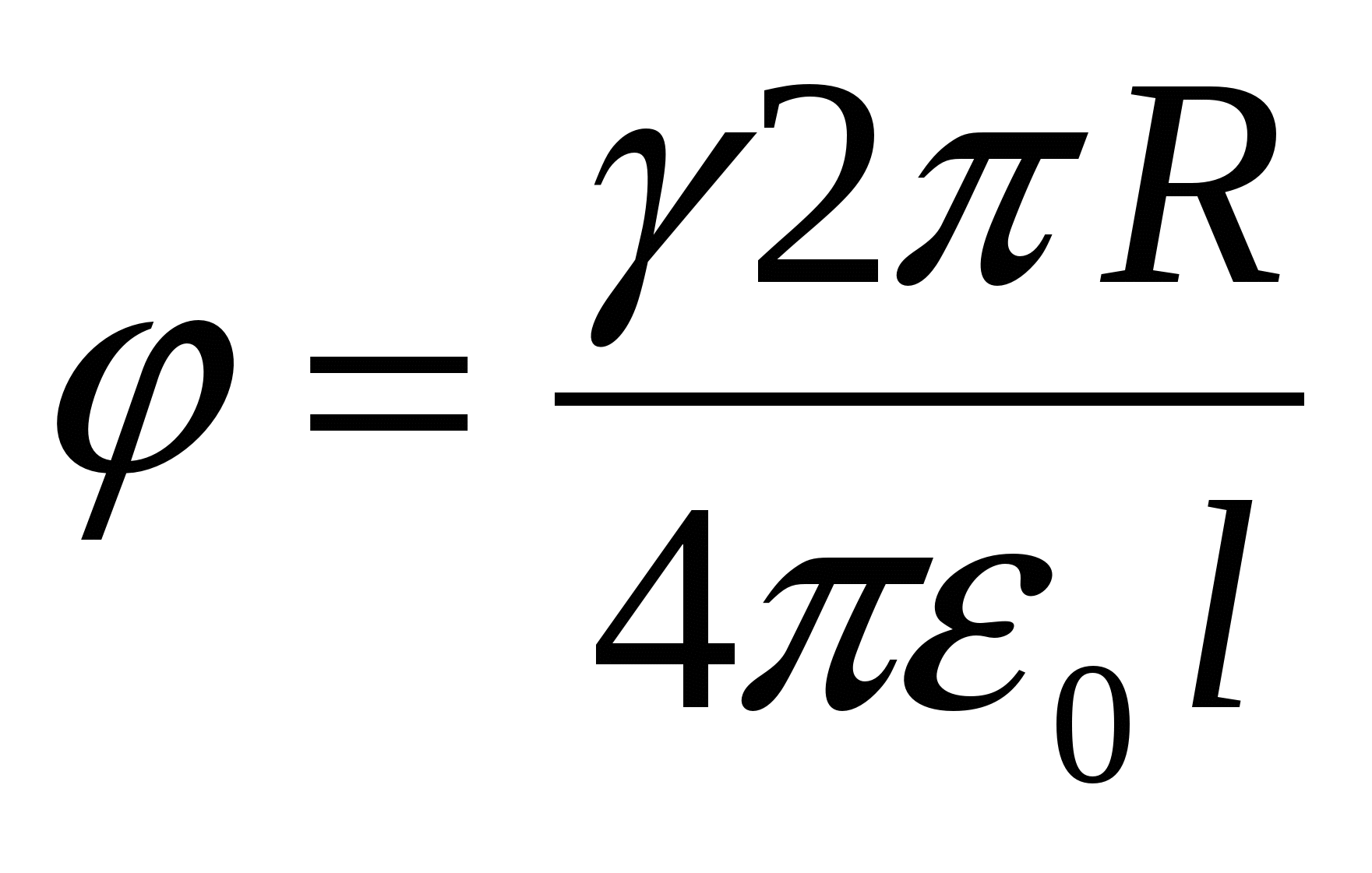 . อย่างไรก็ตามไม่สามารถทำได้เนื่องจากความสมมาตรของประจุไม่ใช่เชิงพื้นที่ แต่เป็นระนาบ อันที่จริงแล้วเราควรแยกแหวนออกเป็นชิ้นเล็กๆ ซึ่งสามารถพิจารณาได้ จุดวัสดุกำหนดศักยภาพของสนามของแต่ละจุดประจุดังกล่าว ณ ตำแหน่งของประจุ + q
และรวมผลลัพธ์:
. อย่างไรก็ตามไม่สามารถทำได้เนื่องจากความสมมาตรของประจุไม่ใช่เชิงพื้นที่ แต่เป็นระนาบ อันที่จริงแล้วเราควรแยกแหวนออกเป็นชิ้นเล็กๆ ซึ่งสามารถพิจารณาได้ จุดวัสดุกำหนดศักยภาพของสนามของแต่ละจุดประจุดังกล่าว ณ ตำแหน่งของประจุ + q
และรวมผลลัพธ์:
พลังงานปฏิสัมพันธ์ของวงแหวนกับประจุและพลังงานจลน์สูงสุดของประจุมีค่าเท่ากัน ตามกฎการอนุรักษ์พลังงาน: 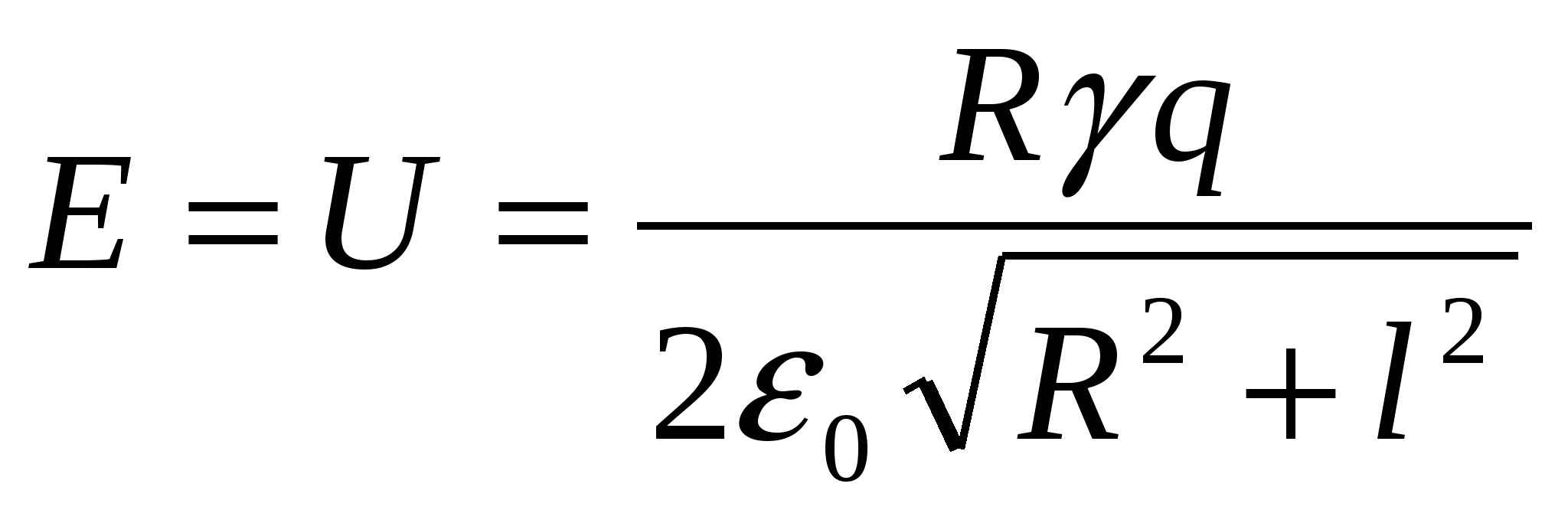 - คำตอบ.
- คำตอบ.
ในทำนองเดียวกัน ศักยภาพที่พบในการแก้ปัญหา A 19 จากการทดสอบหมายเลข 8 ของ TsT 2001: ประจุ 10–9 C จะถูกกระจายอย่างสม่ำเสมอบนวงแหวนลวดเส้นเล็กที่มีรัศมี 3 ซม. กำหนดความต่างศักย์ระหว่างจุดศูนย์กลางของวงแหวนกับจุดบนแกนของวงแหวนที่ระยะห่าง 4 ซม. จากจุดศูนย์กลาง ตอบ: 120 โวลท์
6
(TsT 2000 ทดสอบ 3.A 20) ถ้าเป็นลูกโลหะรัศมี R
1
, อัดแน่นด้วยศักยภาพ φ
1
, เชื่อมต่อแบบบาง
ลวดที่มีลูกโลหะรัศมีที่ไม่มีประจุ R
2 แล้วศักย์รวมของสารประกอบจะเท่ากับ
| 1) 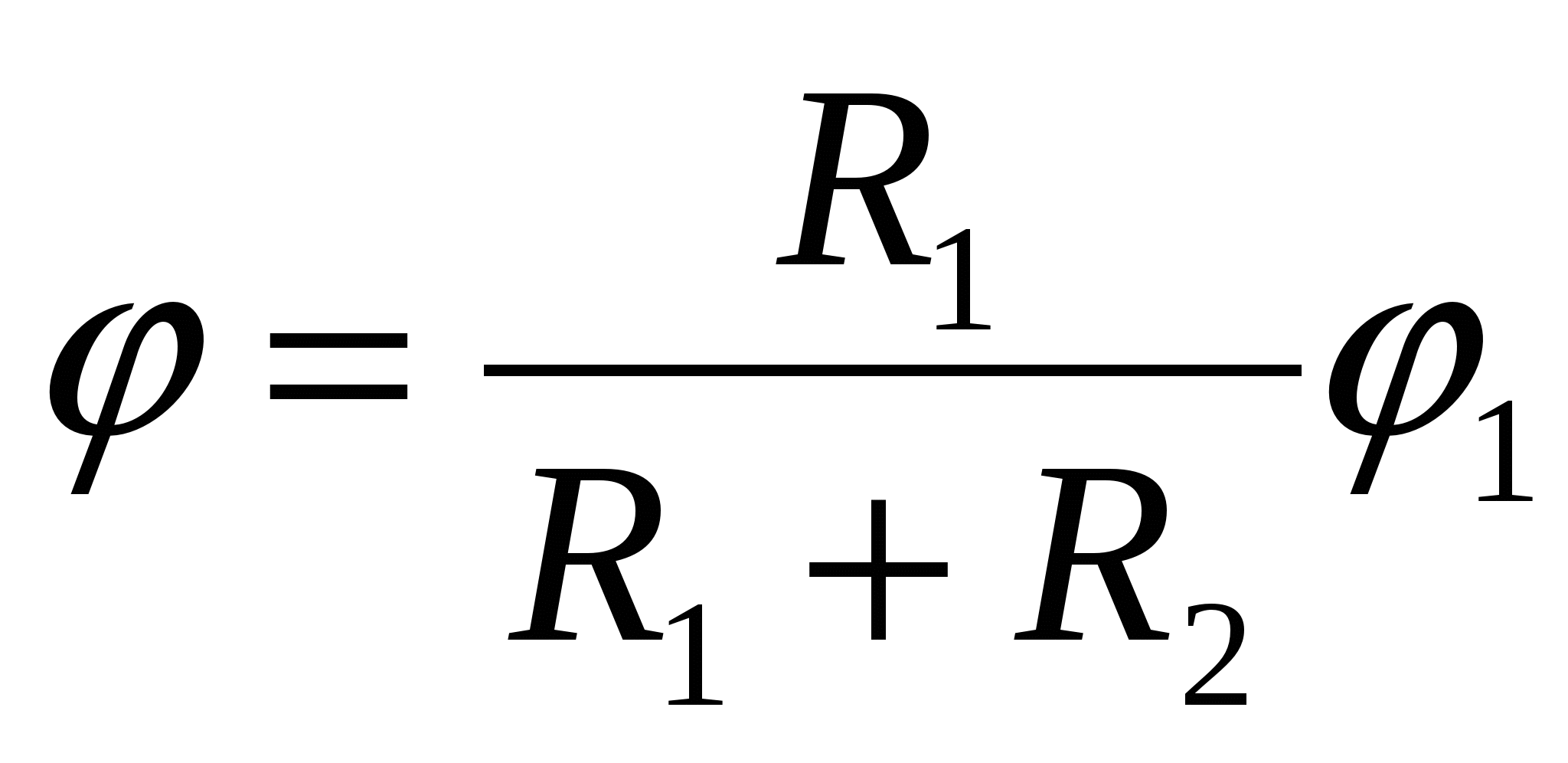 | 2) 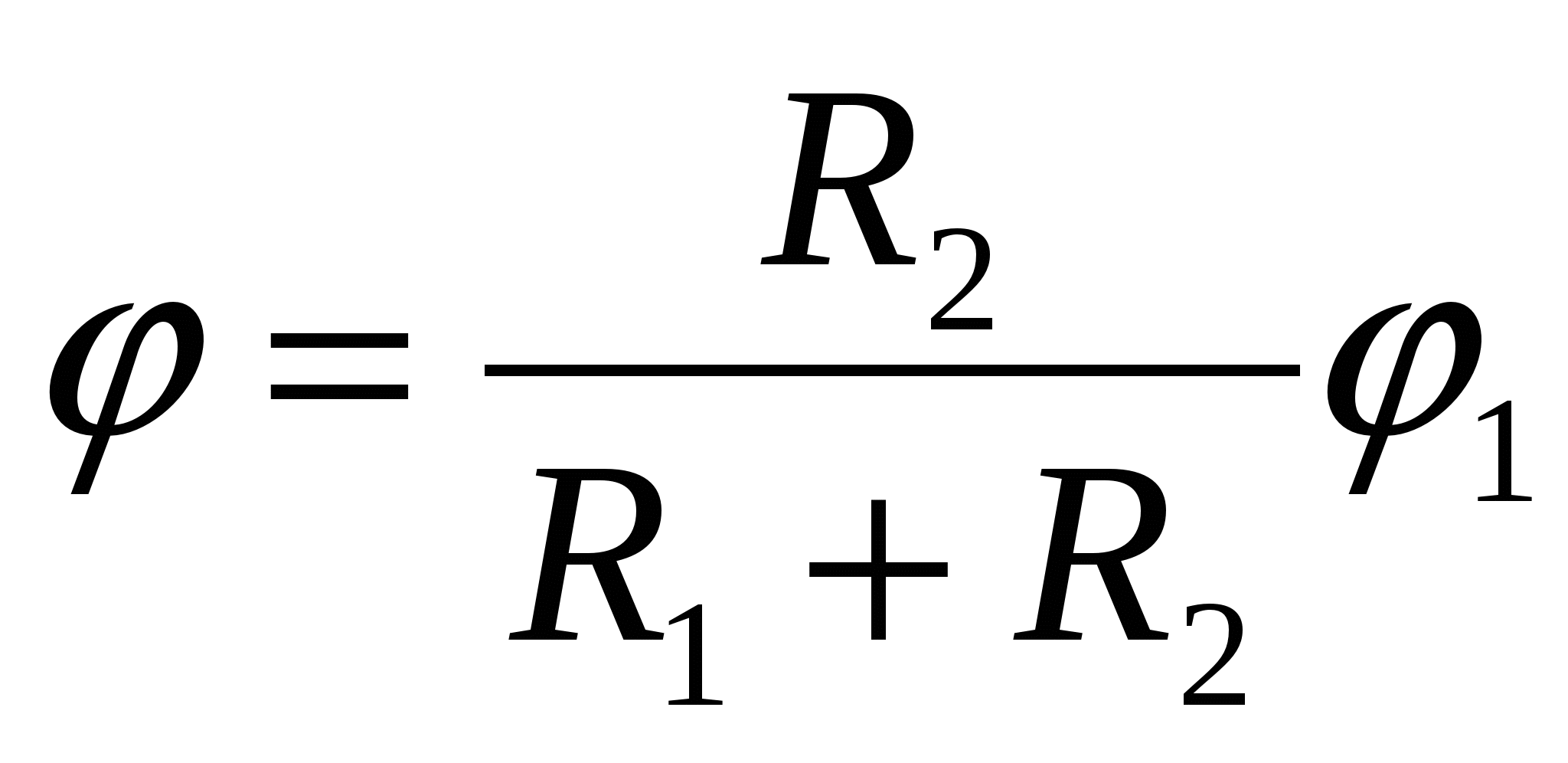 | 3) 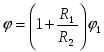 |
| 2) 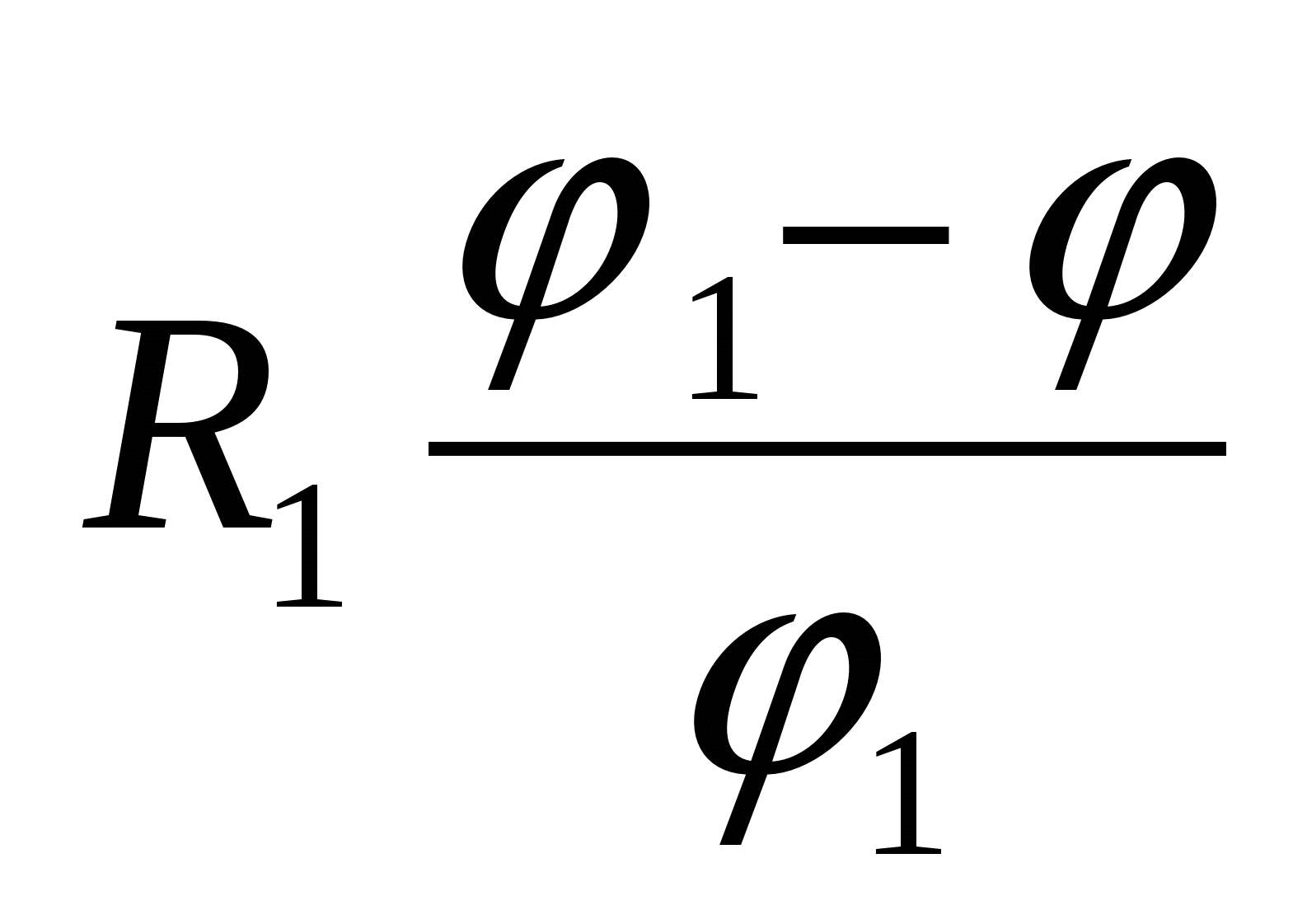 | 3) 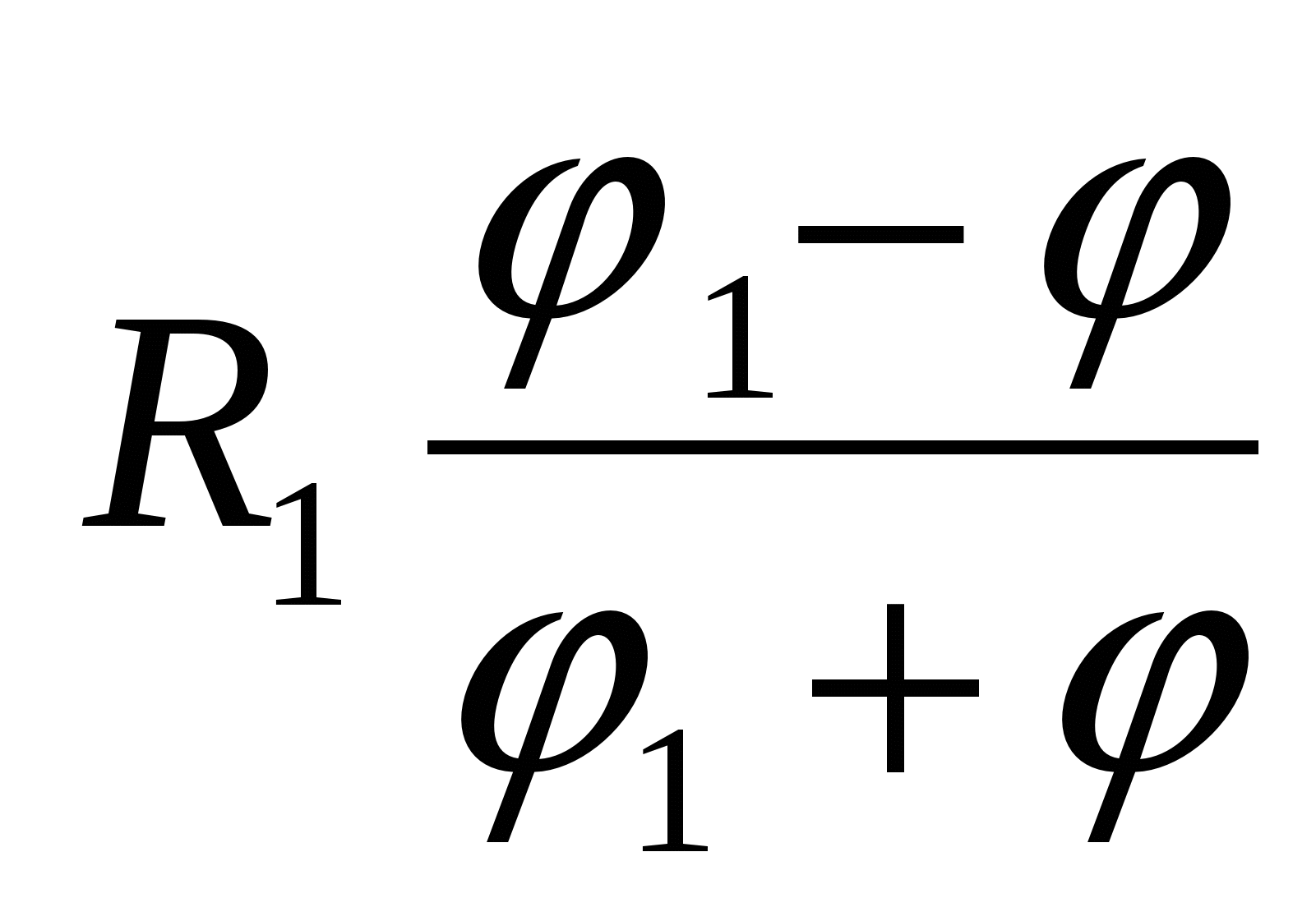 |
|
| 4) 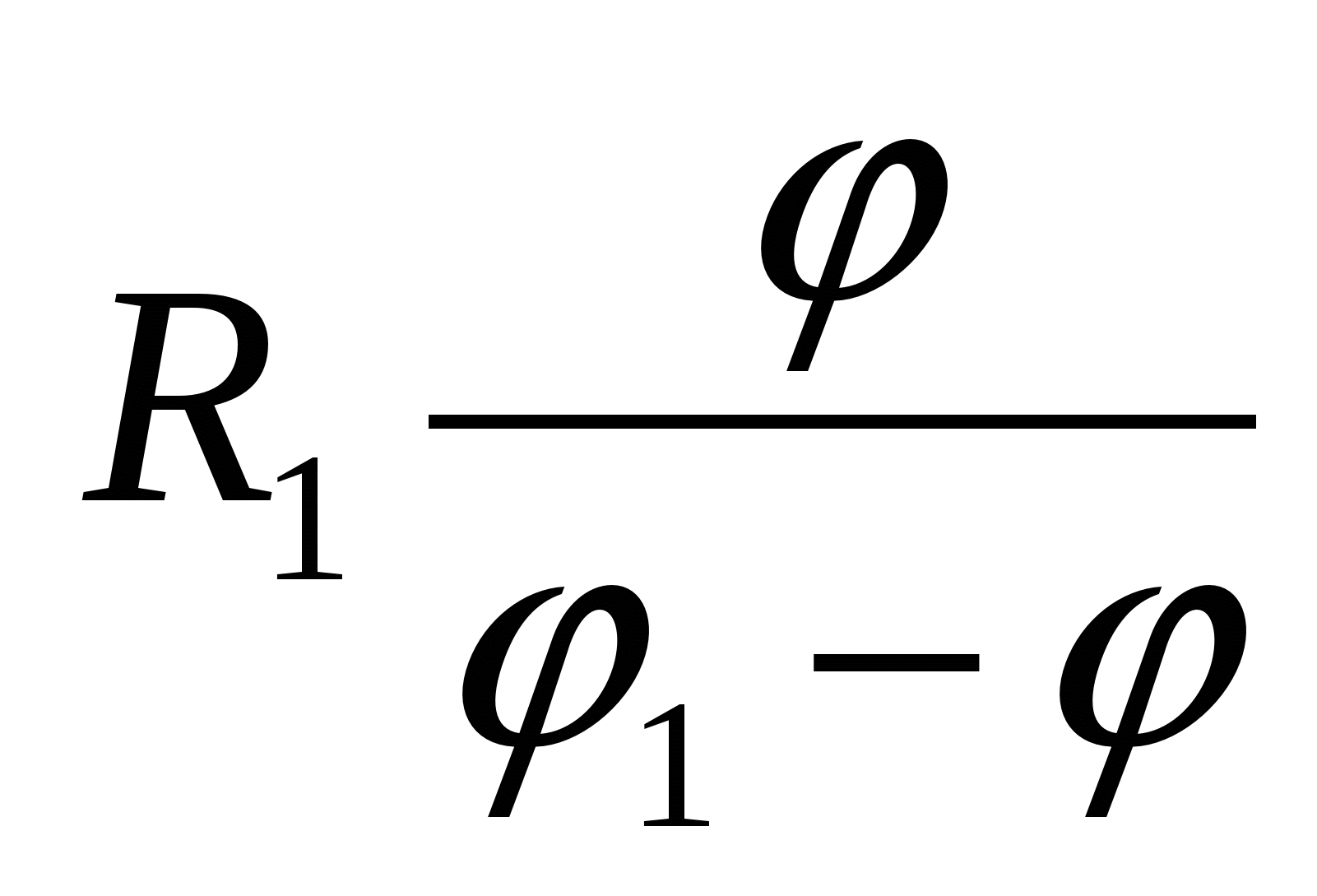 | 5) 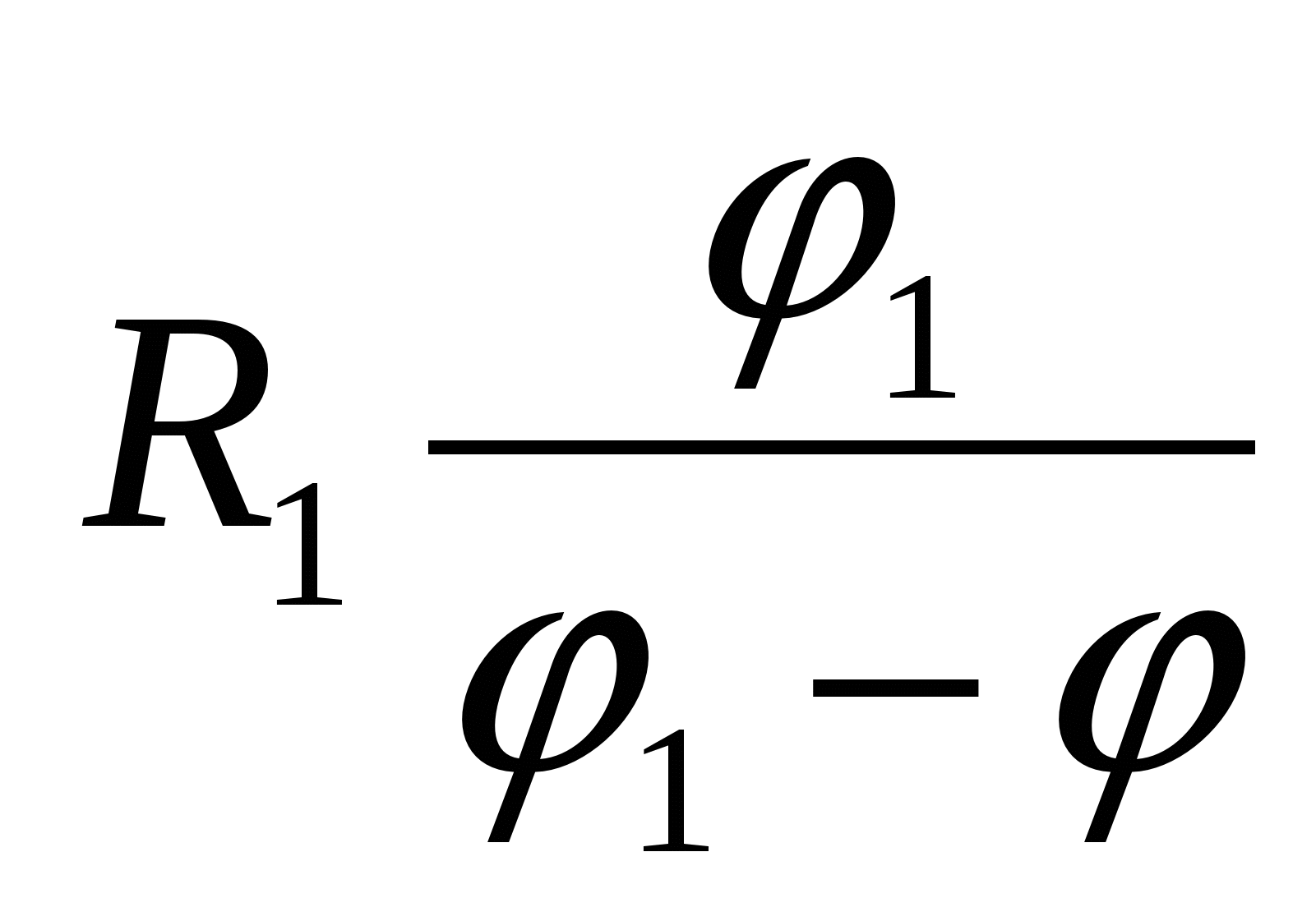 |
7
(CT 2001. ทดสอบ 2. A 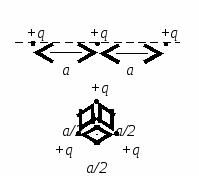 19). ต้องดำเนินการมากน้อยเพียงใดเพื่อให้มีประจุบวกสามจุดเท่ากัน qอยู่ในสุญญากาศตามแนวยาวเส้นเดียว เอ
จากกัน วางไว้ที่จุดยอดของสามเหลี่ยมด้านเท่าที่มีด้าน เอ/2.
19). ต้องดำเนินการมากน้อยเพียงใดเพื่อให้มีประจุบวกสามจุดเท่ากัน qอยู่ในสุญญากาศตามแนวยาวเส้นเดียว เอ
จากกัน วางไว้ที่จุดยอดของสามเหลี่ยมด้านเท่าที่มีด้าน เอ/2.
7.1. มีอิเล็กโทรดสองขั้วในรูปทรงกลมศูนย์กลางที่มีรัศมี เอ(ภายใน) และ ข(ภายนอก). ระบบดังกล่าวเรียกว่าตัวเก็บประจุทรงกลม ค้นหาศักยภาพของจุดใดๆ ในสนามระหว่างอิเล็กโทรด
7.2. คำนวณศักยภาพ สนามไฟฟ้าไดโพล
7.3. ค้นหาศักย์สนามของระบบประจุที่อยู่ในปริมาตรที่มีมิติเชิงเส้น l, ในระยะทาง .
7.4. วาดไดอะแกรมศักย์ของระบบทรงกลมที่มีประจุสองอัน
7.5. คำนวณศักย์สนามของลูกบอลรัศมี เอ, ปริมาตรเท่ากัน: ก) ภายในลูกบอล; b) นอกลูกบอล กราฟรูปภาพ 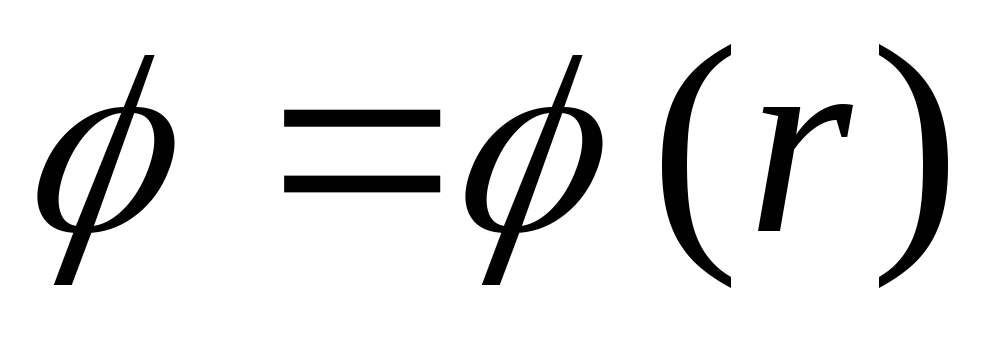 โดยที่ r คือระยะห่างจากศูนย์กลางของลูกบอล แก้ปัญหาโดยการรวมสมการปัวซองในพิกัดทรงกลมและใช้ความสัมพันธ์ระหว่างความแรงของสนามกับศักยภาพ
โดยที่ r คือระยะห่างจากศูนย์กลางของลูกบอล แก้ปัญหาโดยการรวมสมการปัวซองในพิกัดทรงกลมและใช้ความสัมพันธ์ระหว่างความแรงของสนามกับศักยภาพ
7.6. ตามวงแหวนลวดบางรัศมี Rแบ่งจ่ายเท่ากัน q. ตรวจสอบการพึ่งพาศักย์สนามไฟฟ้าบนแกนของวงแหวนที่ระยะห่างจากศูนย์กลาง หาแรงตึงจากการไล่ระดับที่อาจเกิดขึ้น
7.7. รัศมีทรงกลม  , เรียกเก็บเงินอย่างสม่ำเสมอด้วยค่าใช้จ่าย
, เรียกเก็บเงินอย่างสม่ำเสมอด้วยค่าใช้จ่าย 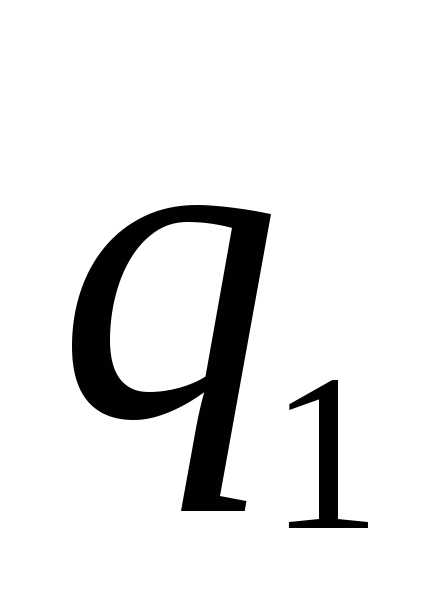 ล้อมรอบด้วยรัศมีทรงกลมบางๆ
ล้อมรอบด้วยรัศมีทรงกลมบางๆ 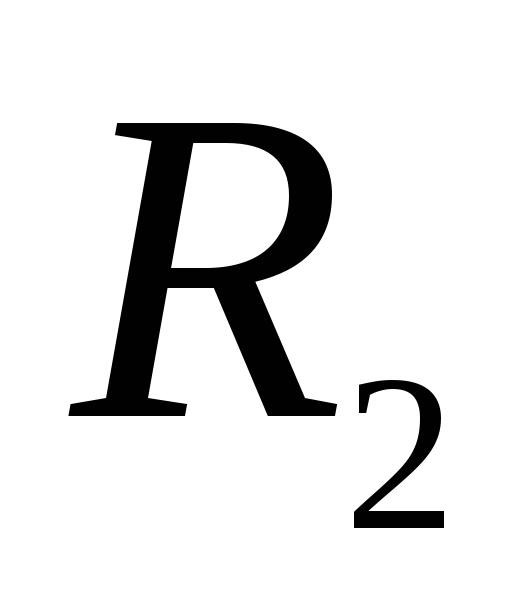 . ค่าอะไร
. ค่าอะไร 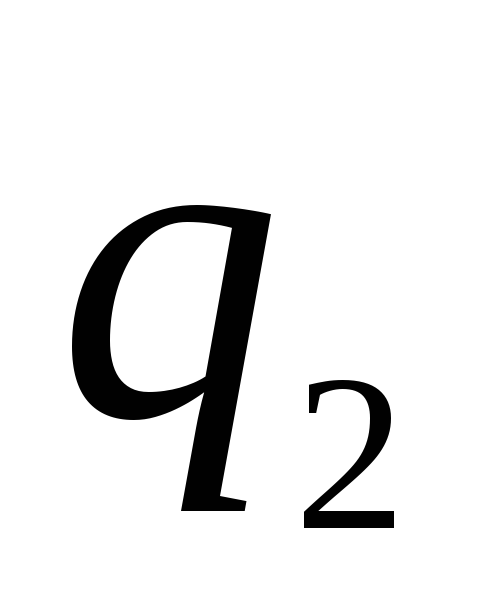 จำเป็นต้องแจ้งทรงกลมชั้นนอกเพื่อให้ศักยภาพของทรงกลมชั้นในเทียบกับอนันต์หายไป? ค่าใช้จ่าย
จำเป็นต้องแจ้งทรงกลมชั้นนอกเพื่อให้ศักยภาพของทรงกลมชั้นในเทียบกับอนันต์หายไป? ค่าใช้จ่าย 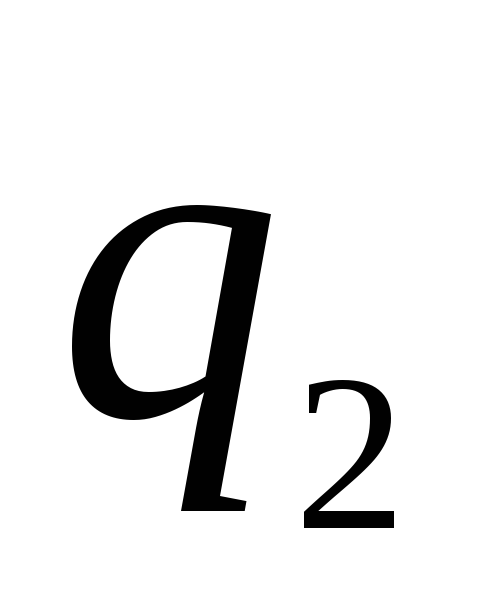 ยังกระจายไปทั่วพื้นผิวของมัน
ยังกระจายไปทั่วพื้นผิวของมัน
การแก้ปัญหา
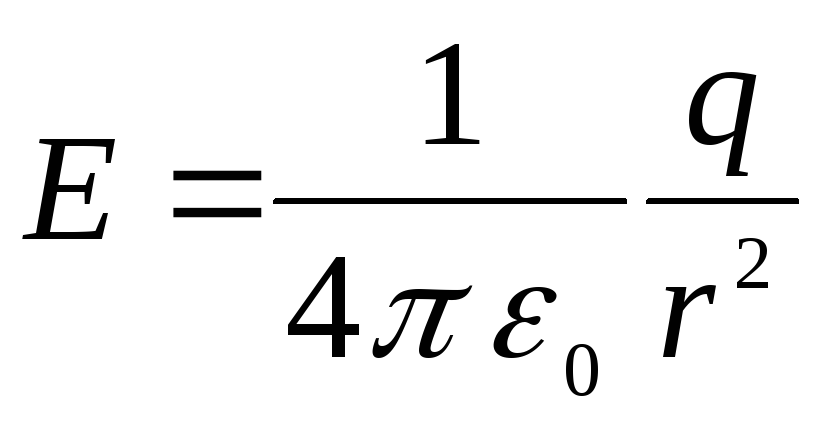
และดังนั้นการเปลี่ยนแปลงในอวกาศในลักษณะเดียวกับในกรณีของสนามที่มีประจุจุดซึ่งตามมาด้วยความต่างศักย์ระหว่างทรงกลมชั้นในกับจุดใด ๆ ของสนามที่อยู่ห่างไกล rจากศูนย์กลางของตัวเก็บประจุเท่ากับ
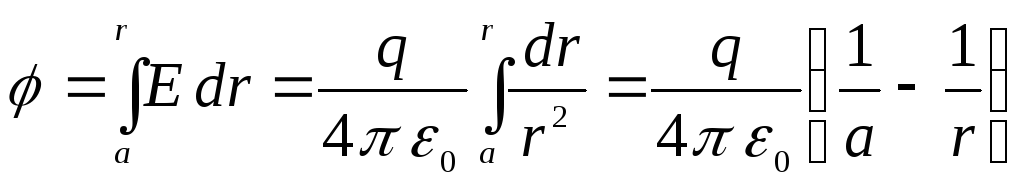 .
.
ความแตกต่างที่อาจเกิดขึ้น 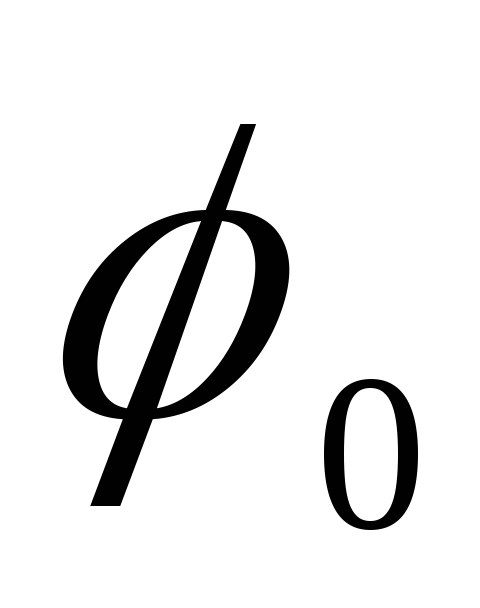 ระหว่างขั้วไฟฟ้า (ทรงกลม) จะเท่ากับ
ระหว่างขั้วไฟฟ้า (ทรงกลม) จะเท่ากับ
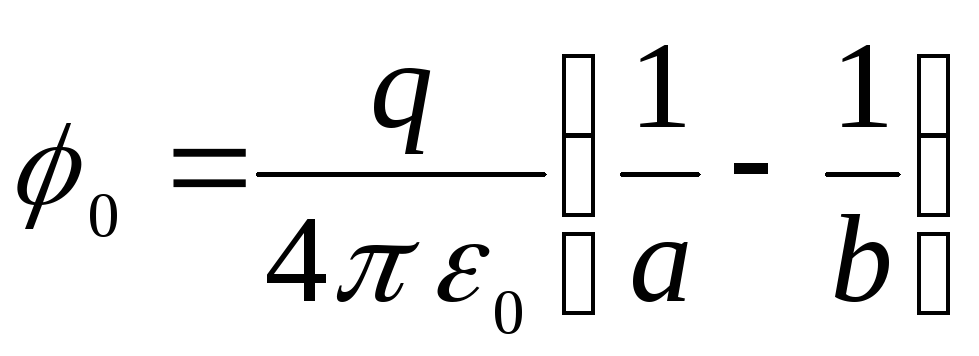 .
.
จากทั้งสองสูตรดังนี้
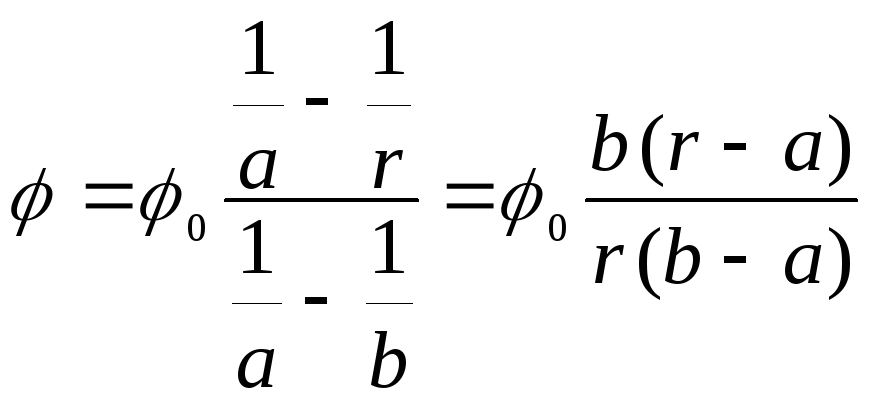 .
.
มีวัด 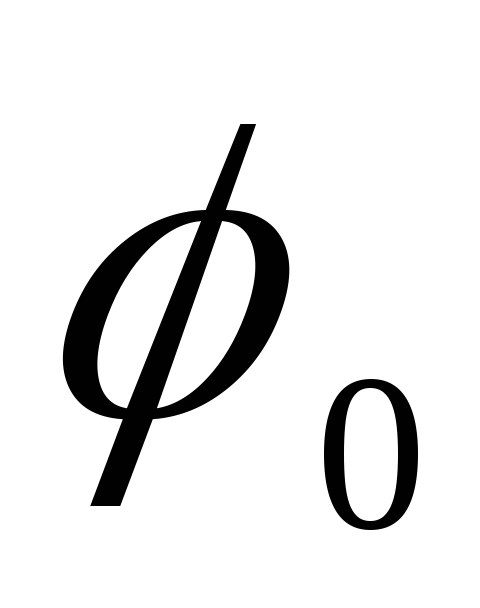 ระหว่างอิเล็กโทรด คุณสามารถคำนวณศักยภาพของจุดใดๆ ในสนามได้
ระหว่างอิเล็กโทรด คุณสามารถคำนวณศักยภาพของจุดใดๆ ในสนามได้
7.2. ให้ระบบการเรียกเก็บเงิน 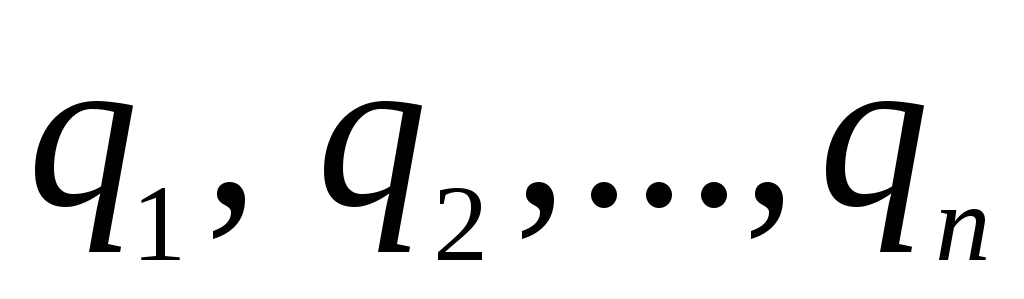 อยู่ในปริมาตรที่มีมิติเชิงเส้น ล. ให้เราหาศักยภาพของสนามที่สร้างขึ้นโดยระบบประจุนี้ในระยะทาง r ที่มีขนาดใหญ่เมื่อเทียบกับ l เราเลือกที่มาของพิกัด O ภายในปริมาตรที่ถูกครอบครองโดยระบบประจุและกำหนดตำแหน่งของประจุโดยใช้รัศมี - เวกเตอร์
อยู่ในปริมาตรที่มีมิติเชิงเส้น ล. ให้เราหาศักยภาพของสนามที่สร้างขึ้นโดยระบบประจุนี้ในระยะทาง r ที่มีขนาดใหญ่เมื่อเทียบกับ l เราเลือกที่มาของพิกัด O ภายในปริมาตรที่ถูกครอบครองโดยระบบประจุและกำหนดตำแหน่งของประจุโดยใช้รัศมี - เวกเตอร์ 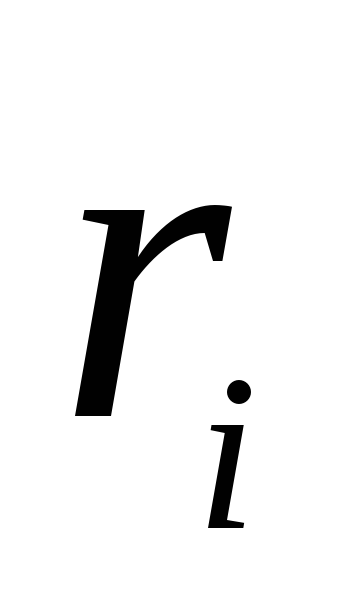 (รูปที่ ___ แสดงเวกเตอร์รัศมีตัวใดตัวหนึ่ง
(รูปที่ ___ แสดงเวกเตอร์รัศมีตัวใดตัวหนึ่ง 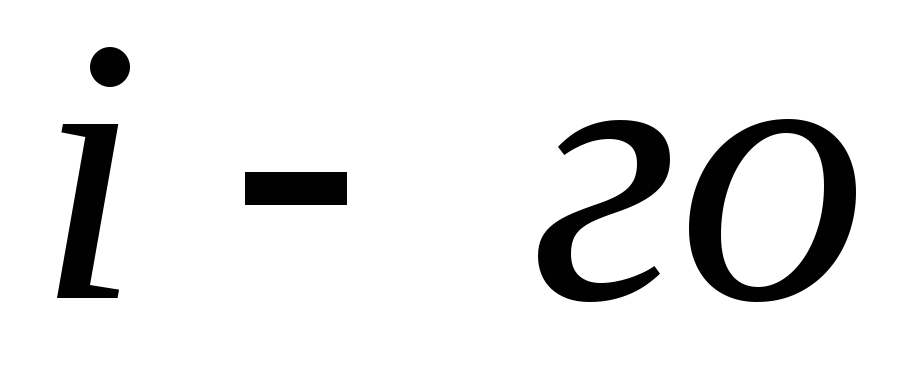 ค่าใช้จ่าย). ศักยภาพ ณ จุดที่กำหนดโดยเวกเตอร์รัศมี
ค่าใช้จ่าย). ศักยภาพ ณ จุดที่กำหนดโดยเวกเตอร์รัศมี 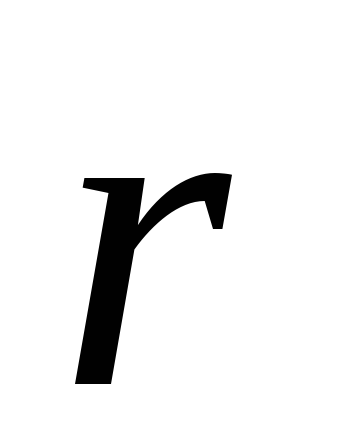 , เท่ากับ
, เท่ากับ
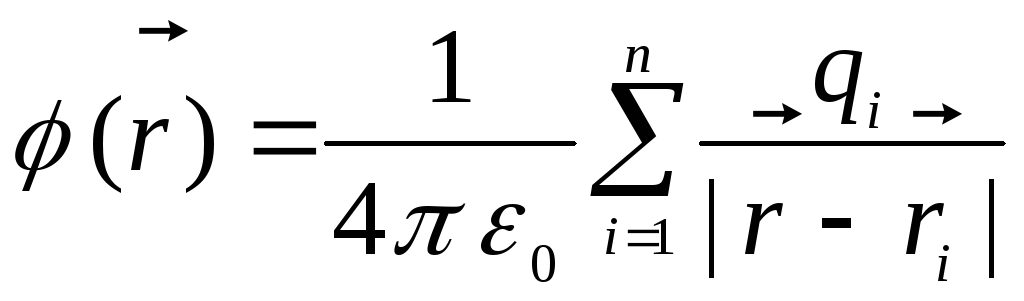 .
.
เพราะ 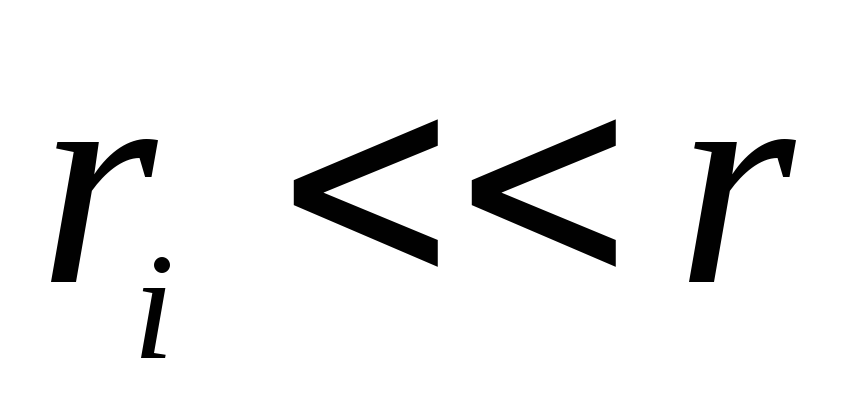 , จากนั้นเราสามารถใส่ว่า
, จากนั้นเราสามารถใส่ว่า
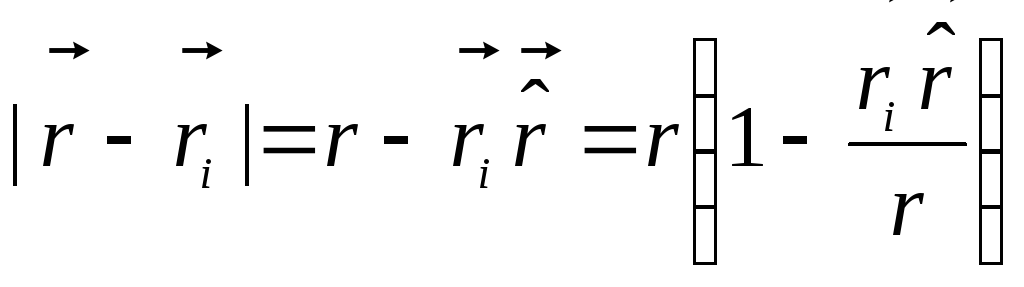
(เครื่องหมาย 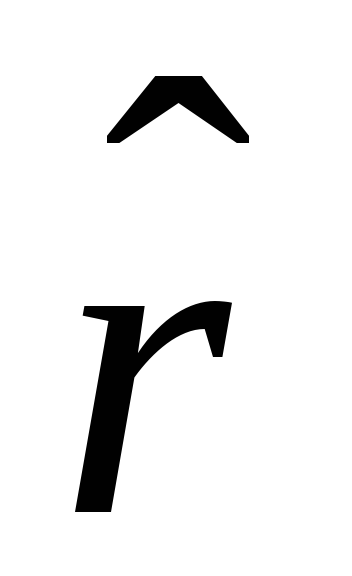 เราแทนเวกเตอร์หน่วย) แล้ว
เราแทนเวกเตอร์หน่วย) แล้ว
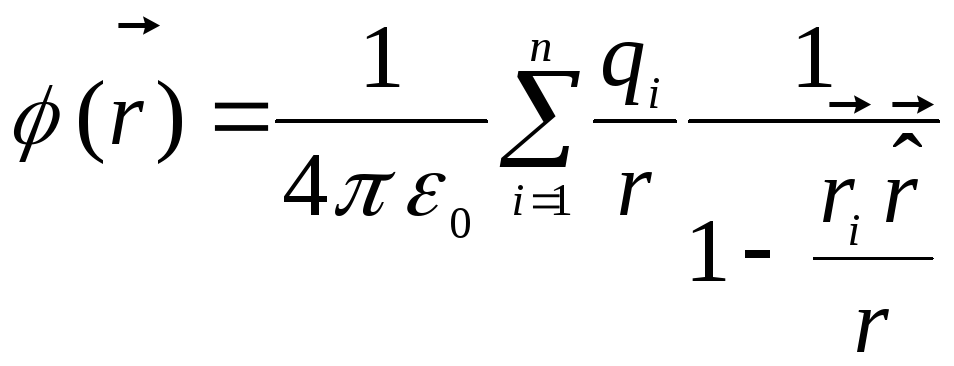 .
.
มาใช้สูตรกัน
![]()
ที่ 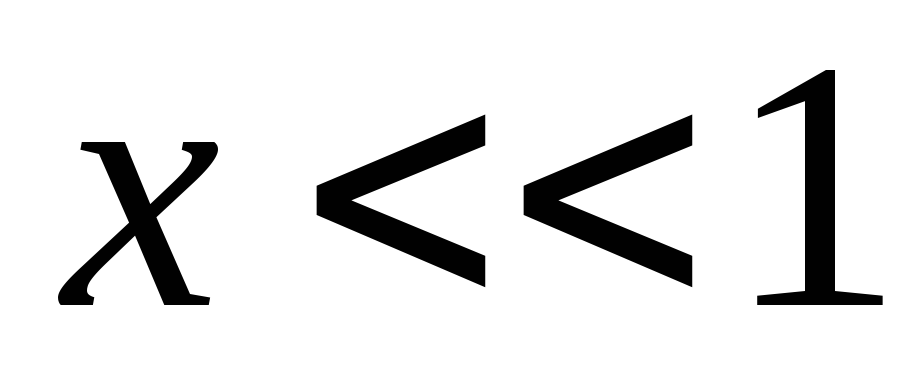 .
.
ตอนนี้เขียนได้
เทอมแรกของนิพจน์นี้คือศักยภาพของสนามของจุดประจุที่มีค่า 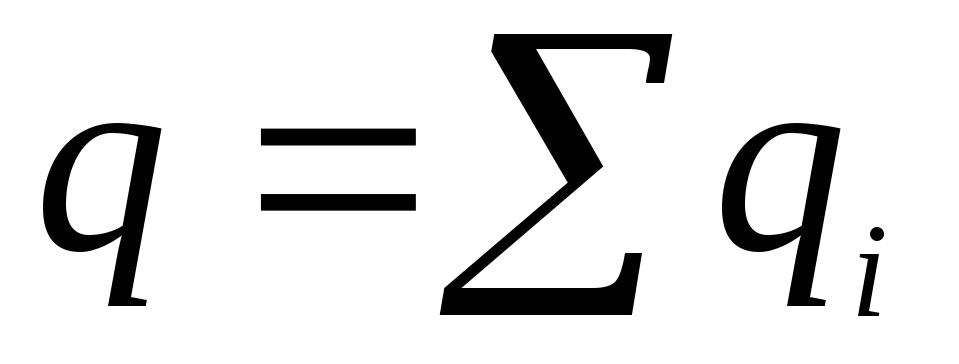 . เทอมที่สองมีรูปแบบเดียวกับนิพจน์ที่กำหนดศักยภาพของสนามไดโพล ปริมาณเล่นบทบาทของโมเมนต์ไฟฟ้าของไดโพล
. เทอมที่สองมีรูปแบบเดียวกับนิพจน์ที่กำหนดศักยภาพของสนามไดโพล ปริมาณเล่นบทบาทของโมเมนต์ไฟฟ้าของไดโพล
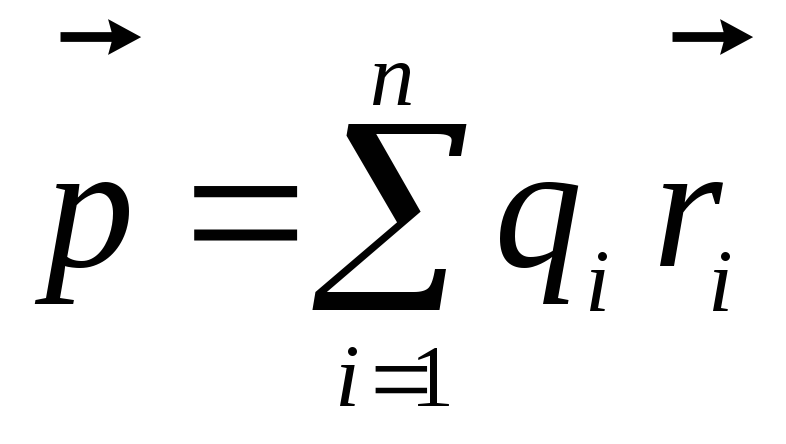 ,
,
ซึ่งเรียกว่าโมเมนต์ไดโพลไฟฟ้าของระบบประจุ
7.3. หากฟิลด์ถูกสร้างขึ้นโดยการชาร์จหลายครั้ง ศักยภาพของฟิลด์นี้จะเท่ากับผลรวมของศักยภาพของฟิลด์ที่สร้างขึ้นโดยการชาร์จแต่ละครั้ง
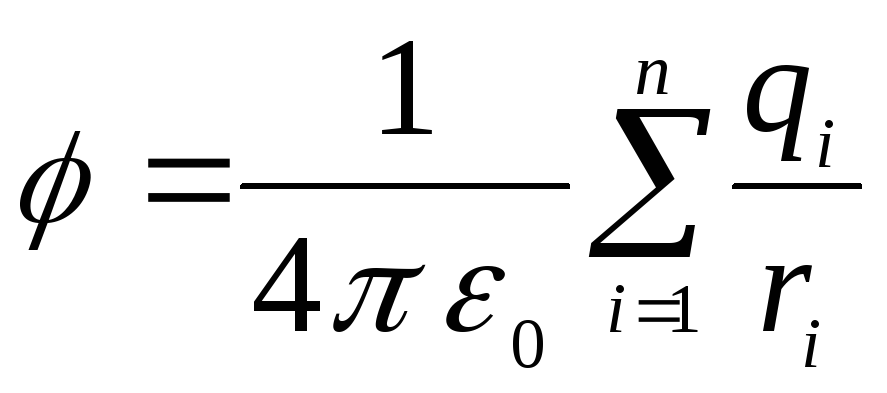
ที่นี่  คือ ศักยภาพของสนามผลลัพธ์ ณ จุดที่พิจารณาเทียบกับอนันต์
คือ ศักยภาพของสนามผลลัพธ์ ณ จุดที่พิจารณาเทียบกับอนันต์ 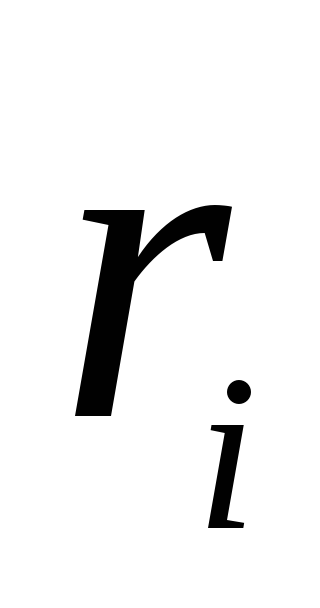 คือระยะทางจากจุดนี้ถึง
คือระยะทางจากจุดนี้ถึง 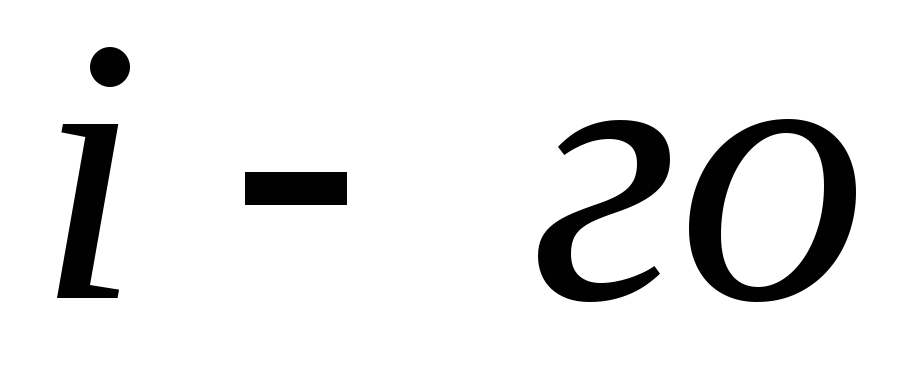 ประจุ และยอดรวมจะดำเนินการกับประจุทุกจุด
ประจุ และยอดรวมจะดำเนินการกับประจุทุกจุด
สนามที่พิจารณามีความสมมาตรตามแนวแกน ดังนั้นรูปแบบสนามในระนาบใดๆ ที่ผ่านแกนไดโพลจะเหมือนกัน และเวกเตอร์  อยู่ในเครื่องบินลำนี้ ตำแหน่งของจุด M ที่สัมพันธ์กับไดโพลจะถูกกำหนดลักษณะโดยใช้เวกเตอร์รัศมี
อยู่ในเครื่องบินลำนี้ ตำแหน่งของจุด M ที่สัมพันธ์กับไดโพลจะถูกกำหนดลักษณะโดยใช้เวกเตอร์รัศมี 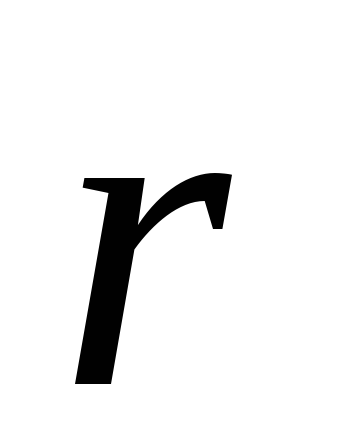 หรือใช้พิกัดเชิงขั้ว r และ
หรือใช้พิกัดเชิงขั้ว r และ  . ตำแหน่งการชาร์จ
. ตำแหน่งการชาร์จ 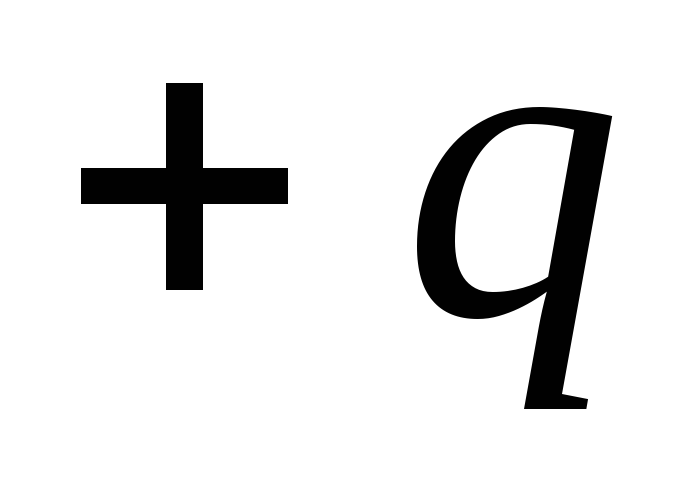 สัมพันธ์กับจุดศูนย์กลางของไดโพลถูกกำหนดโดยเวกเตอร์
สัมพันธ์กับจุดศูนย์กลางของไดโพลถูกกำหนดโดยเวกเตอร์  และค่าใช้จ่าย
และค่าใช้จ่าย 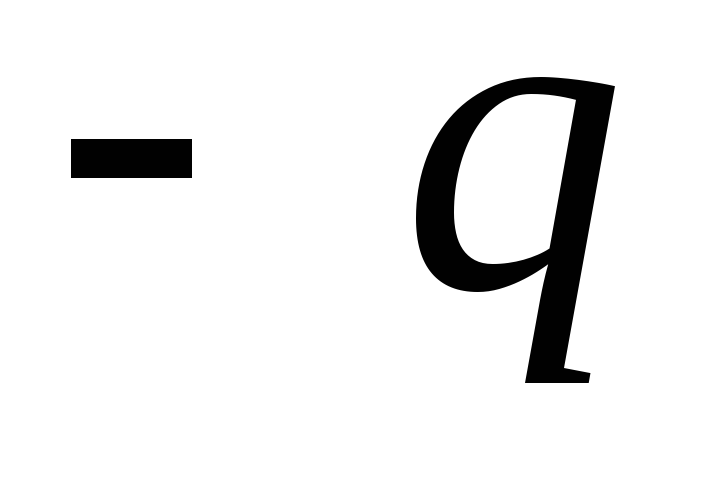 – เวกเตอร์
– เวกเตอร์ 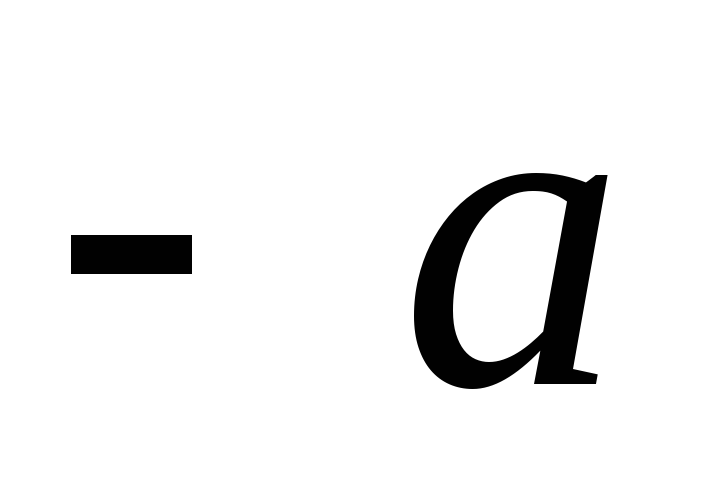 . เห็นได้ชัดว่า
. เห็นได้ชัดว่า 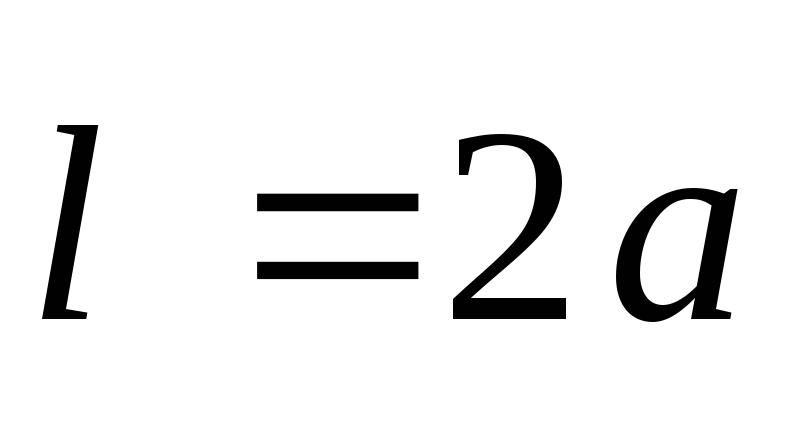 , ที่ไหน
, ที่ไหน 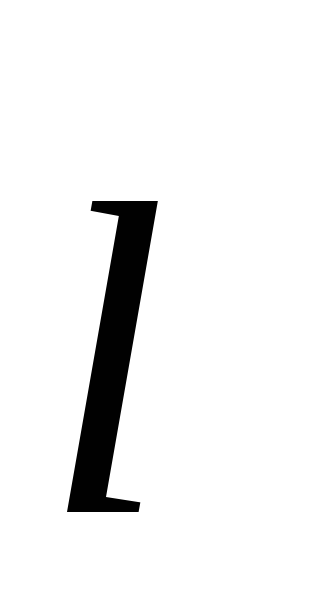 คือแขนของไดโพล ระยะทางจากค่าใช้จ่าย
คือแขนของไดโพล ระยะทางจากค่าใช้จ่าย 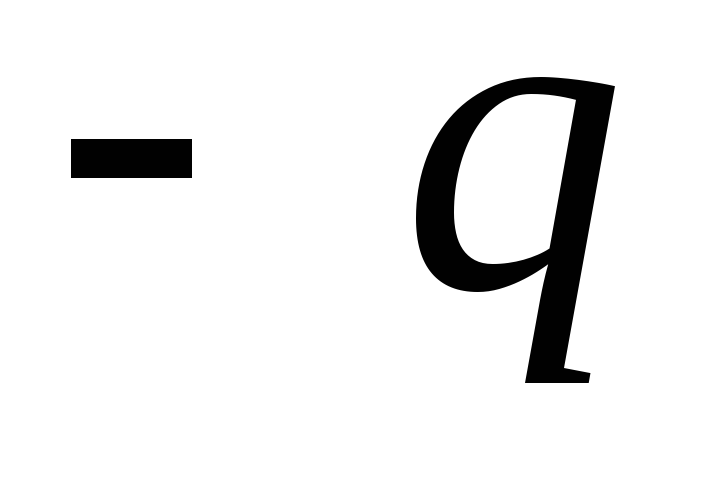 และ
และ 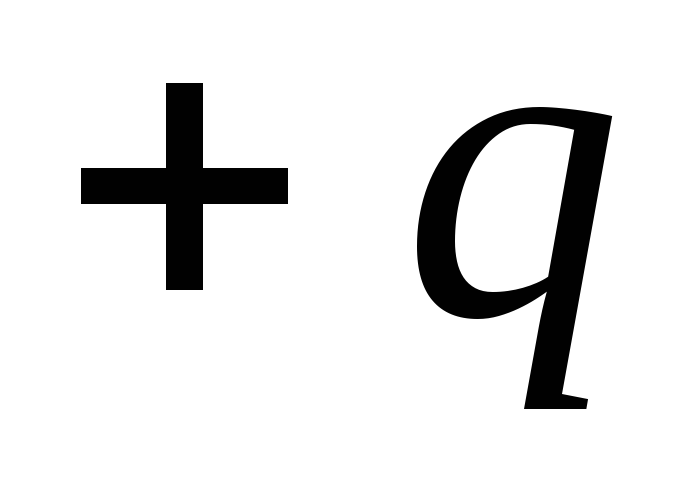 ถึงจุดที่เลือก M เราแสดงตามลำดับ
ถึงจุดที่เลือก M เราแสดงตามลำดับ 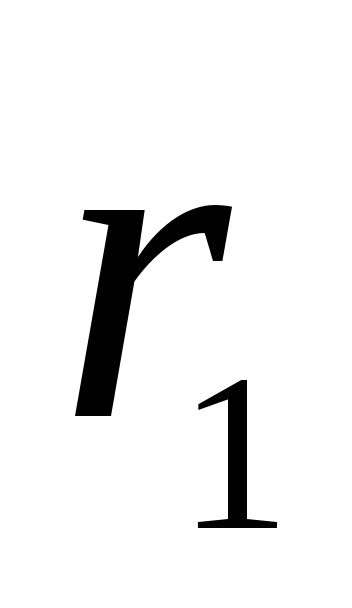 และ
และ 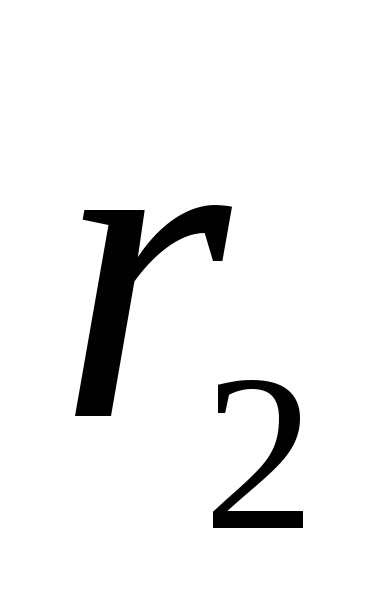 . เพราะ
. เพราะ 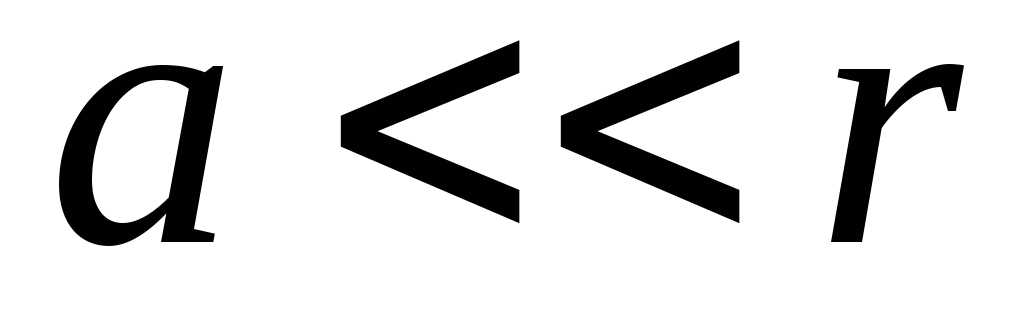 , จากนั้นเราสามารถใส่ว่า
, จากนั้นเราสามารถใส่ว่า
ศักยภาพ ณ จุดที่กำหนดโดยเวกเตอร์รัศมี 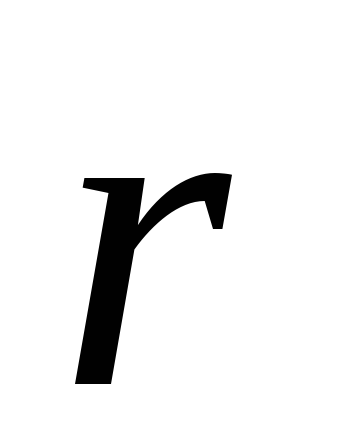 , เท่ากับ
, เท่ากับ
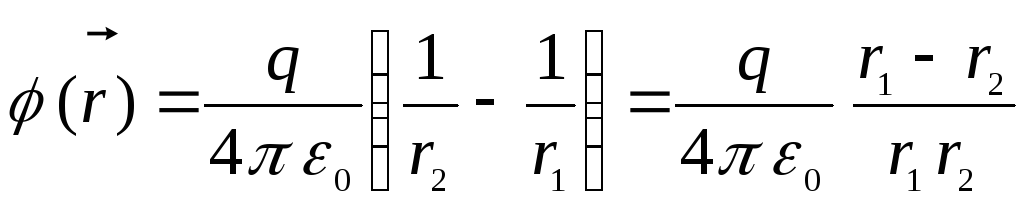 .
.
ทำงาน 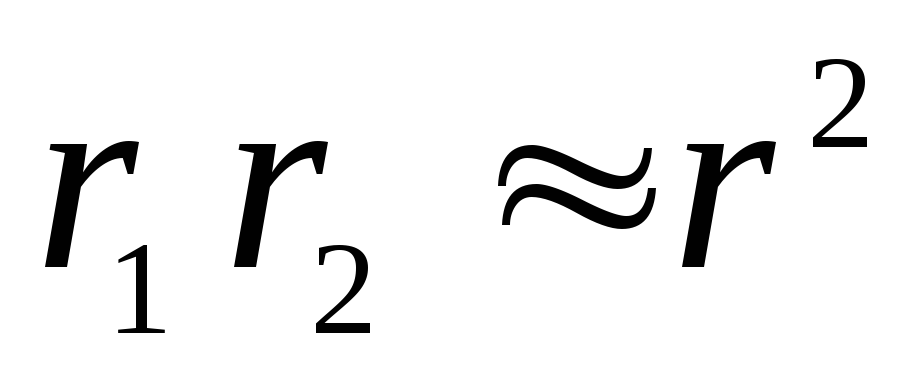 , ความแตกต่าง
, ความแตกต่าง 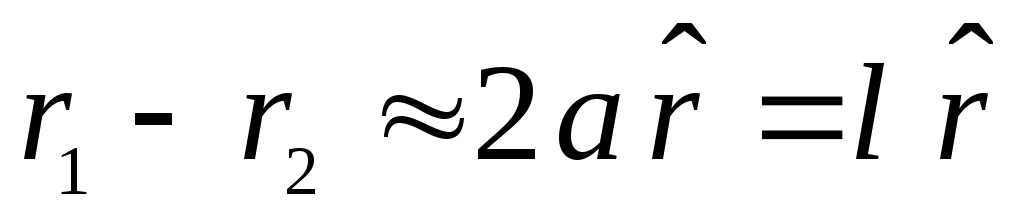 . เพราะเหตุนี้,
. เพราะเหตุนี้,
![]() ,
,
ที่ไหน 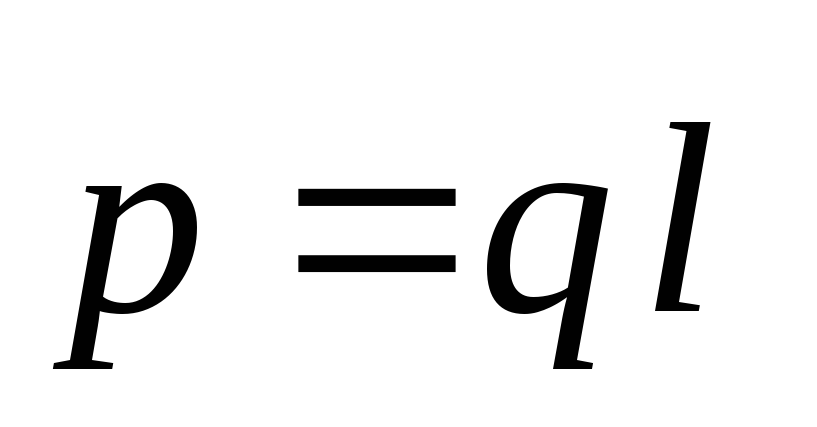 คือโมเมนต์ไฟฟ้าของไดโพล
คือโมเมนต์ไฟฟ้าของไดโพล
จากสูตรนี้จะเห็นได้ว่าศักยภาพของสนามไดโพลถูกกำหนดโดยโมเมนต์ไฟฟ้าของมัน เมื่อเปรียบเทียบศักย์ของสนามไดโพลกับศักย์สนามของประจุแบบจุดจะเห็นว่าศักย์ของสนามไดโพลลดลงตามระยะทางที่เร็วขึ้น 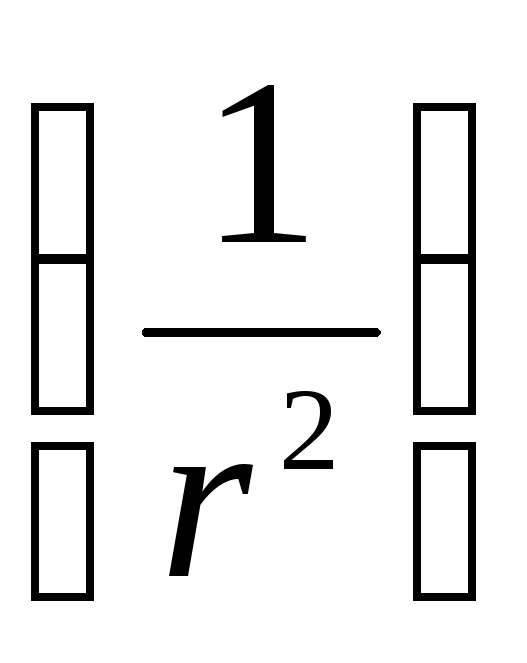 มากกว่าศักย์สนามของประจุแบบจุด
มากกว่าศักย์สนามของประจุแบบจุด 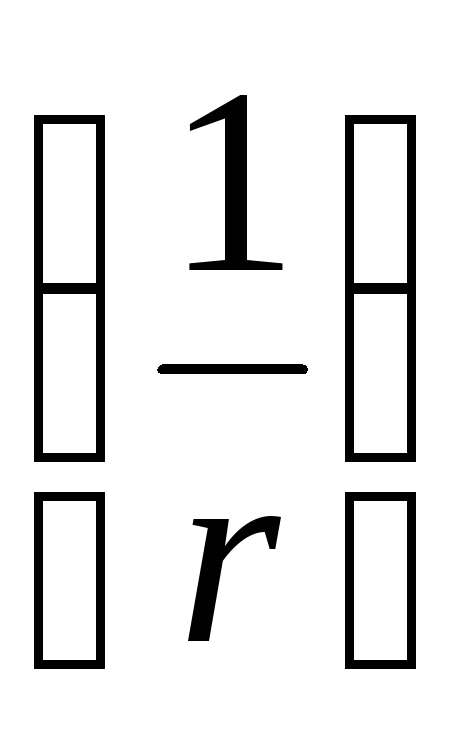 .
.
รูปที่ ___ แสดงว่า 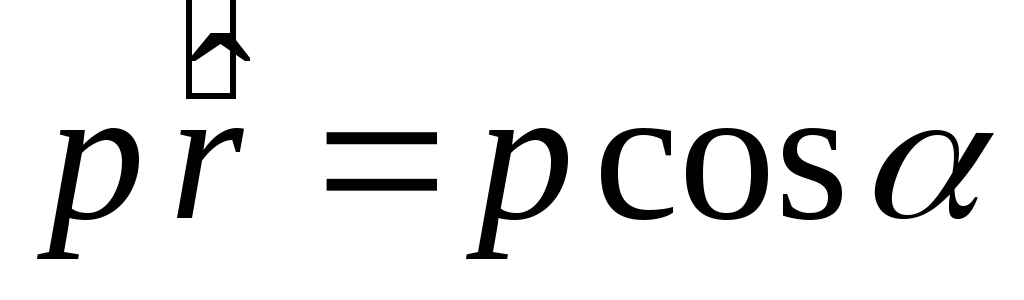 . นั่นเป็นเหตุผลที่
. นั่นเป็นเหตุผลที่
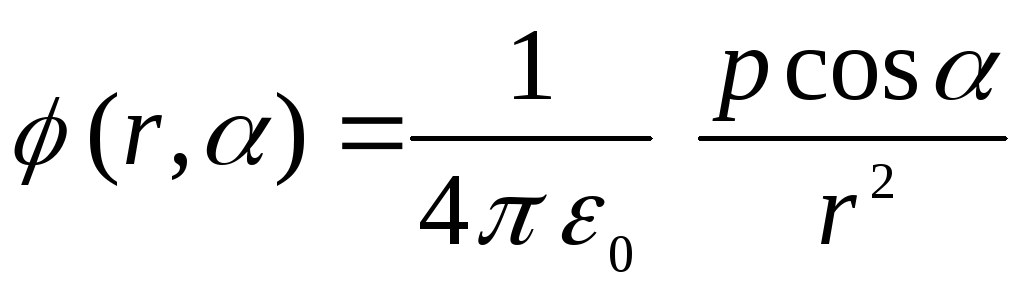 .
.
7.4. ให้ทรงกลมภายในซึ่งมีรัศมี  , มีประจุบวก
, มีประจุบวก 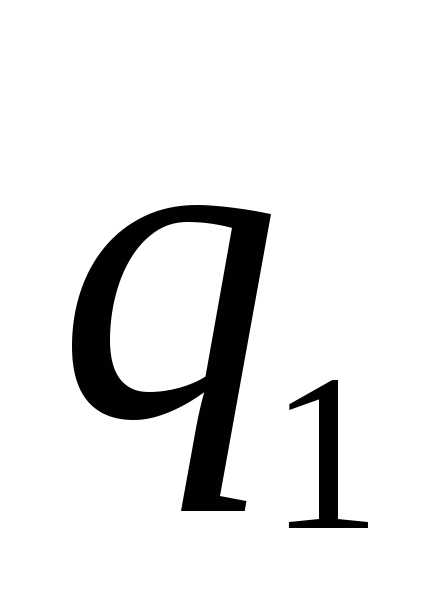 และด้านนอกมีรัศมี
และด้านนอกมีรัศมี 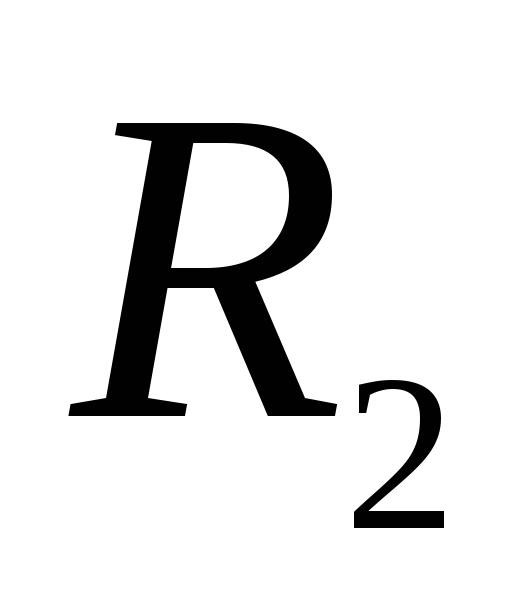 - ประจุลบ
- ประจุลบ 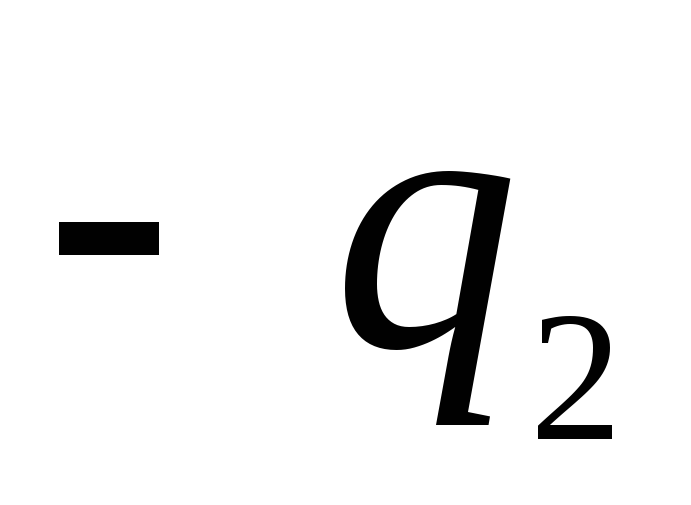 , และ
, และ 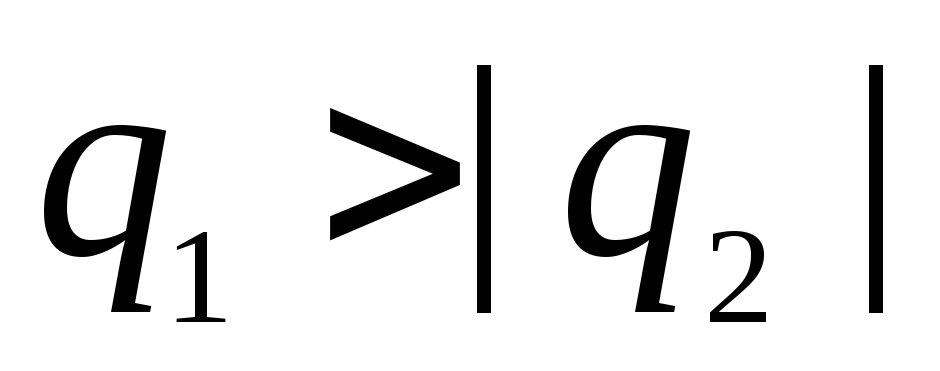 .
.
นอกทรงกลมศักยภาพจะเท่ากับ
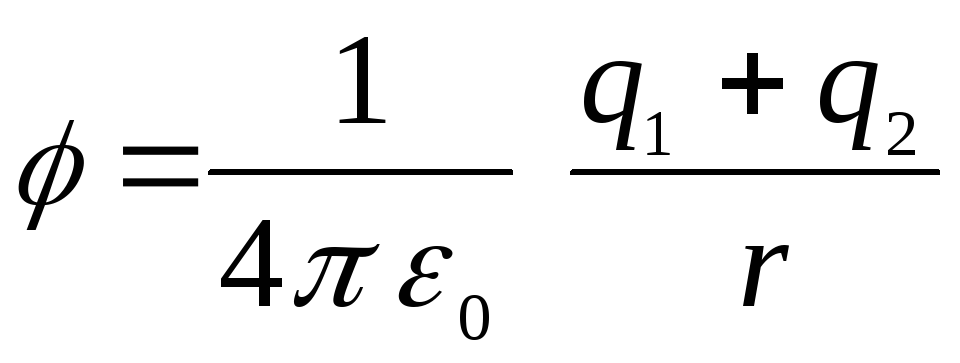 ,
,
เนื่องจากมันถูกสร้างขึ้นร่วมกันโดยทรงกลมทั้งสอง (ศักยภาพคืองานของแรงภายนอกที่เกิดขึ้นเมื่อประจุบวกของหน่วยเคลื่อนที่จากอนันต์ไปยังจุดที่กำหนดของสนาม) งานย้ายประจุบวกหน่วยจากอนันต์ไปยังพื้นที่ระหว่างทรงกลมจะเท่ากับผลรวมของสองงาน: 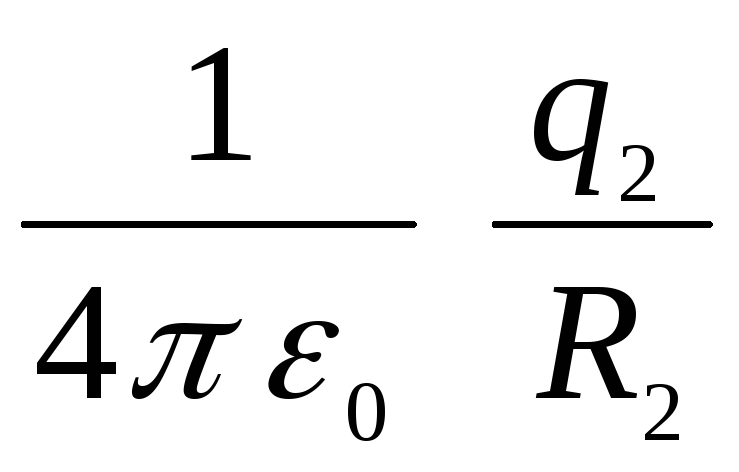 (ทำงานกับแรงที่กระทำจากทรงกลมด้านนอกระหว่างทางจากอนันต์สู่พื้นผิวของมัน) และ
(ทำงานกับแรงที่กระทำจากทรงกลมด้านนอกระหว่างทางจากอนันต์สู่พื้นผิวของมัน) และ 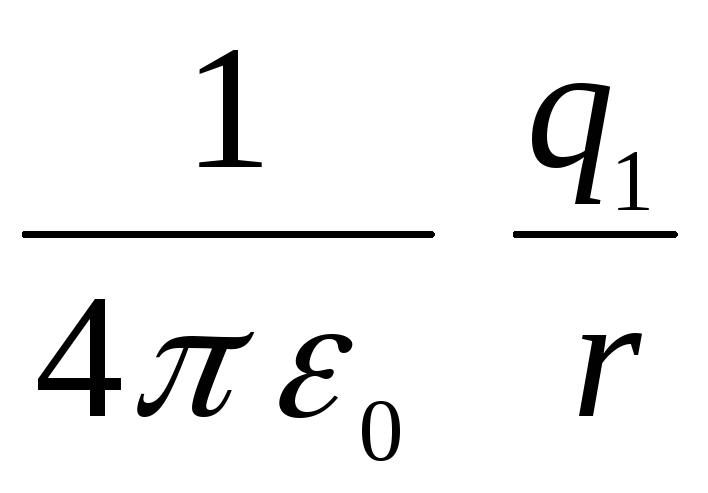 (ทำงานกับสนามของทรงกลมชั้นใน) เช่น
(ทำงานกับสนามของทรงกลมชั้นใน) เช่น
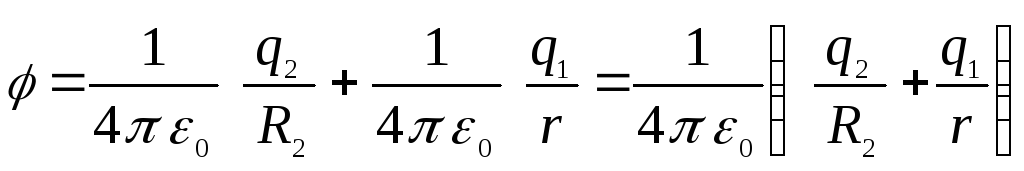 .
.
ภายในทรงกลมที่เล็กกว่า ศักย์จะคงที่และเท่ากับ
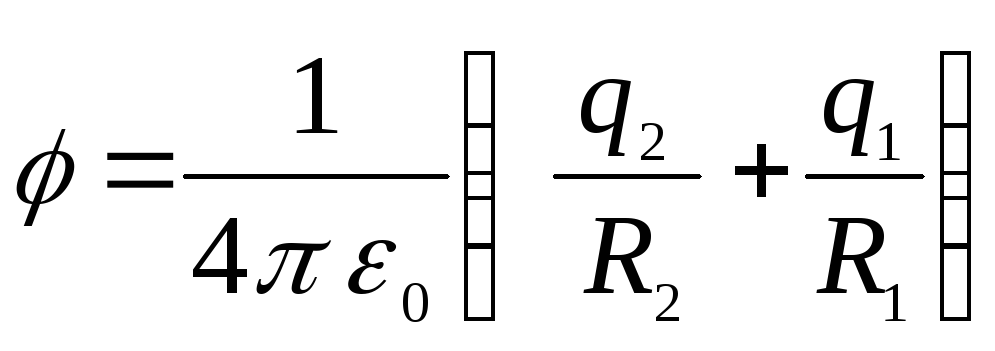 .
.
กราฟที่สร้างตามสูตรแรกและสูตรที่สองแสดงในรูปที่ ____1
หากประจุของทรงกลมมีขนาดเท่ากันและมีเครื่องหมายตรงข้ามกัน กล่าวคือ 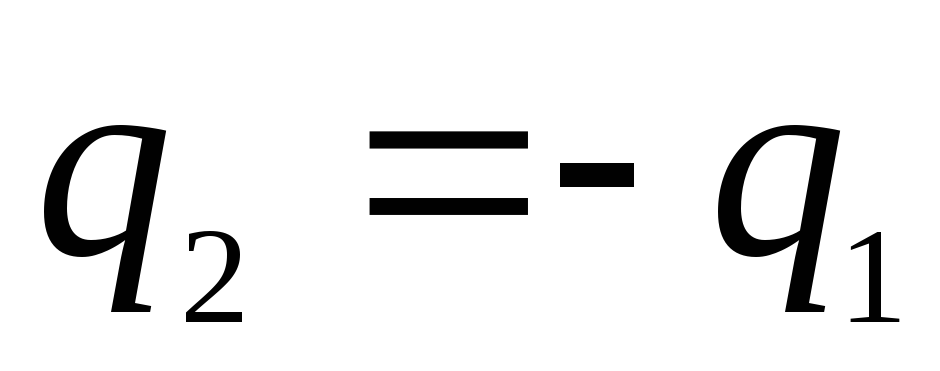 (ระบบดังกล่าวเรียกว่า คาปาซิเตอร์ทรงกลม) จากนั้นศักย์ที่บริเวณรอบนอกจะหายไป และระหว่างเพลตคือ
(ระบบดังกล่าวเรียกว่า คาปาซิเตอร์ทรงกลม) จากนั้นศักย์ที่บริเวณรอบนอกจะหายไป และระหว่างเพลตคือ
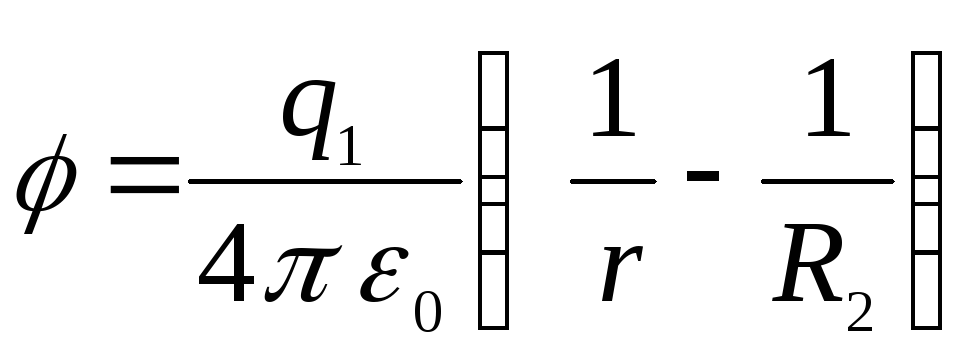 .
.
ปรากฎกราฟที่แสดงในรูปที่ ___2
หากทรงกลมชั้นในมีประจุลบและทรงกลมชั้นนอกมีประจุบวก กราฟจะกลับด้านและดูเหมือนในรูปที่ ____3
7.5. การรวมสมการปัวซองในพิกัดทรงกลม เราแนะนำระบบพิกัดทรงกลม 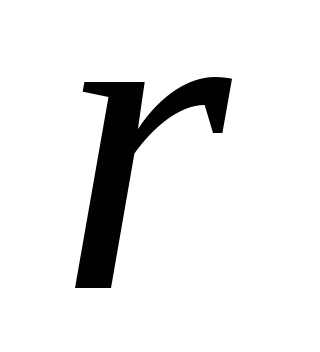 ,
, ,
, โดยเอาศูนย์กลางของลูกเป็นจุดเริ่มต้น สมการเกาส์ในรูปแบบดิฟเฟอเรนเชียล (สมการปัวซอง) ซึ่งกำหนดศักย์สนาม อยู่ในรูปแบบ
โดยเอาศูนย์กลางของลูกเป็นจุดเริ่มต้น สมการเกาส์ในรูปแบบดิฟเฟอเรนเชียล (สมการปัวซอง) ซึ่งกำหนดศักย์สนาม อยู่ในรูปแบบ
ที่ไหน 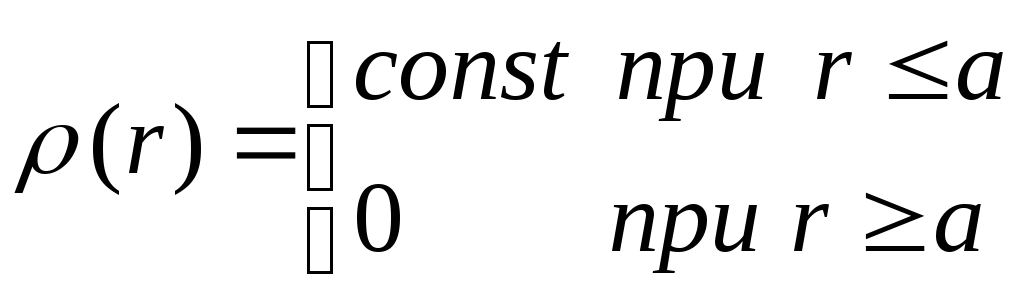 .
.
เนื่องจากการกระจายประจุแบบสมมาตรทรงกลม ศักยภาพ  ขึ้นอยู่กับระยะทาง r เท่านั้นและไม่ขึ้นอยู่กับมุม
ขึ้นอยู่กับระยะทาง r เท่านั้นและไม่ขึ้นอยู่กับมุม  และ
และ  , เช่น.
, เช่น. 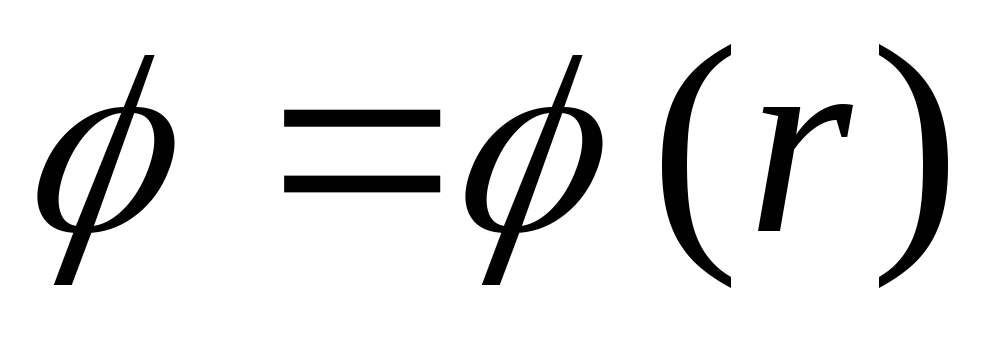 . ดังนั้นสมการปัวซองจึงถูกทำให้ง่ายขึ้นและใช้รูปแบบ
. ดังนั้นสมการปัวซองจึงถูกทำให้ง่ายขึ้นและใช้รูปแบบ
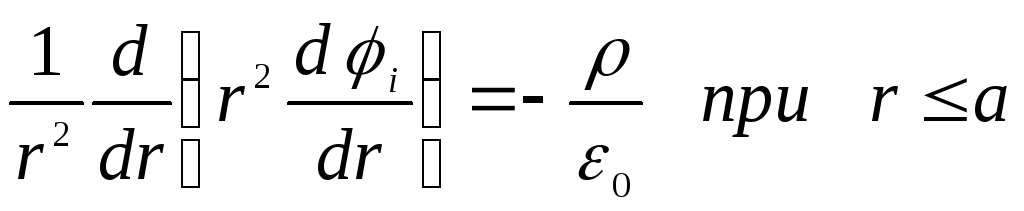
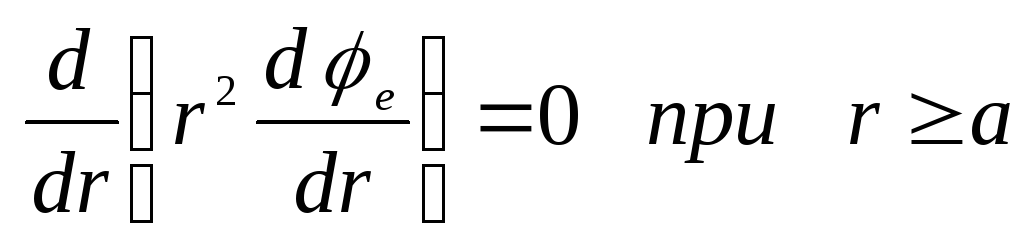 .
.
ที่นี่ผ่าน 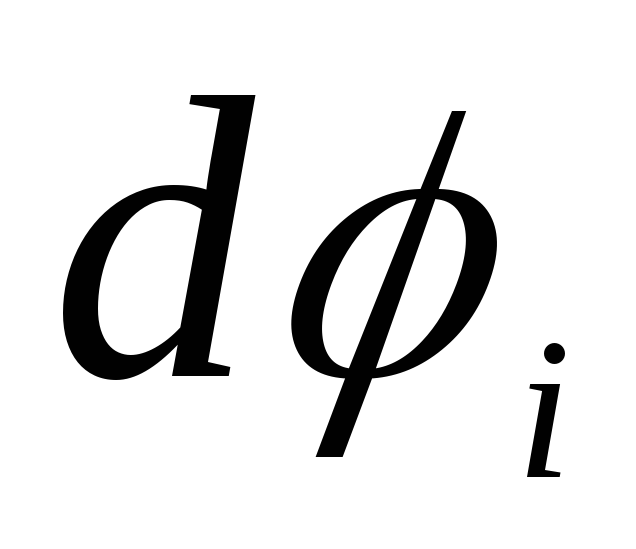 แสดงถึงศักยภาพภายในลูกบอลและทะลุ
แสดงถึงศักยภาพภายในลูกบอลและทะลุ 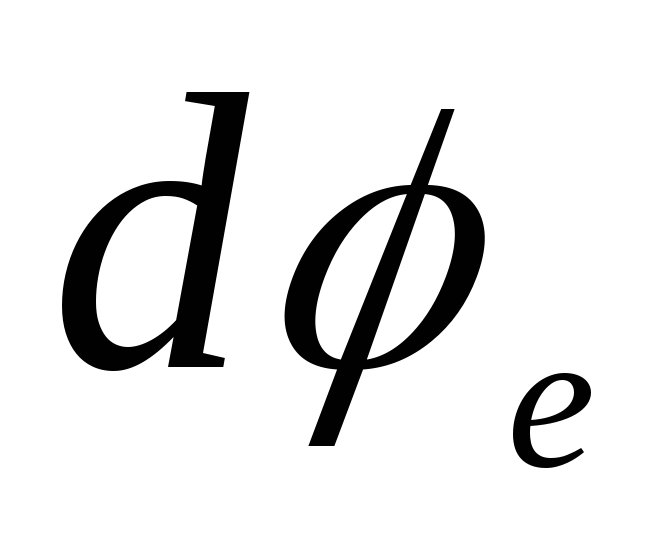 - นอกลูก เมื่อรวมสมการเหล่านี้เข้าด้วยกัน เราพบว่า
- นอกลูก เมื่อรวมสมการเหล่านี้เข้าด้วยกัน เราพบว่า
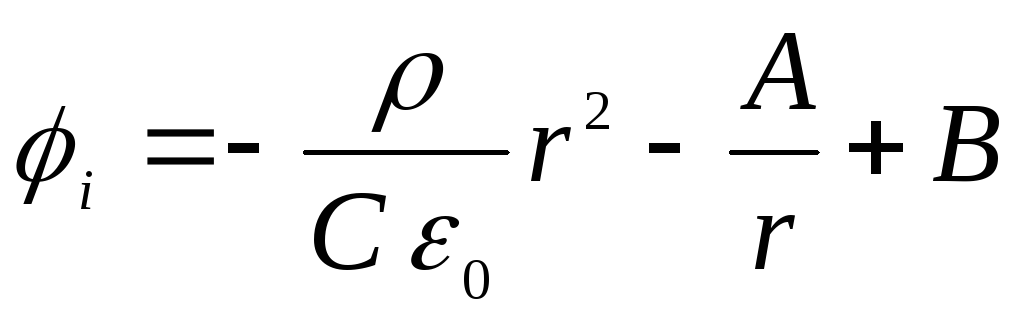 ,
,
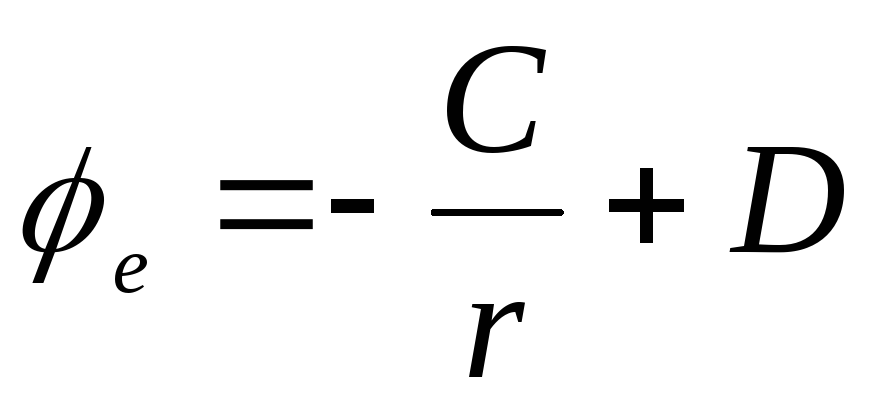 .
.
ค่าคงที่ A, B, C, D ต้องถูกกำหนดจากเงื่อนไขขอบเขตต่อไปนี้
1) ศักยภาพ  ต้องคงอยู่อย่างจำกัด
ต้องคงอยู่อย่างจำกัด 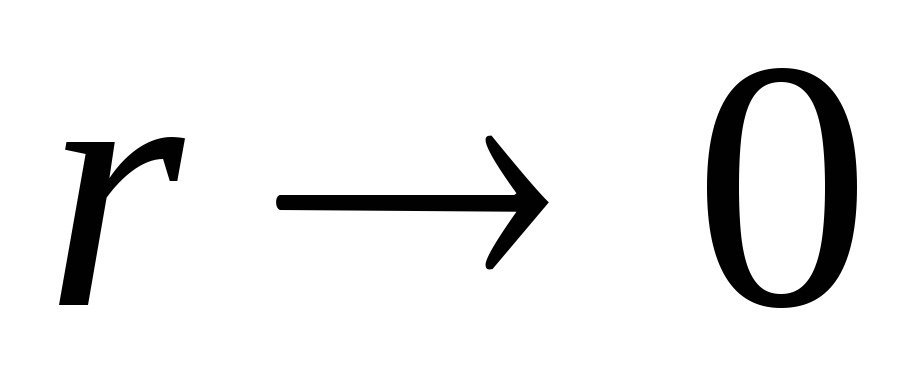 ซึ่งมีความหมายโดยตรงว่า
ซึ่งมีความหมายโดยตรงว่า 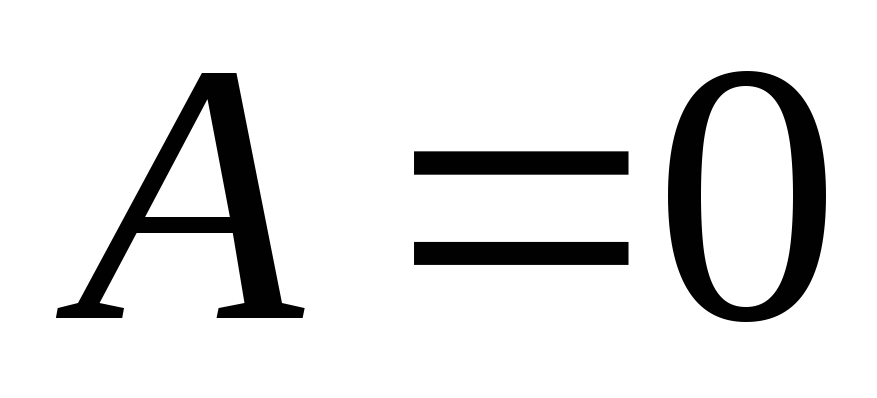 .
.
2)
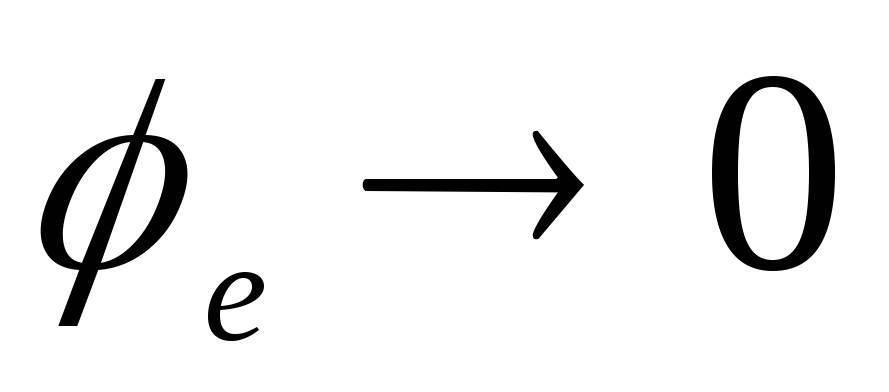 ที่
ที่  , ดังนั้นจึงเป็นไปตามนั้น
, ดังนั้นจึงเป็นไปตามนั้น 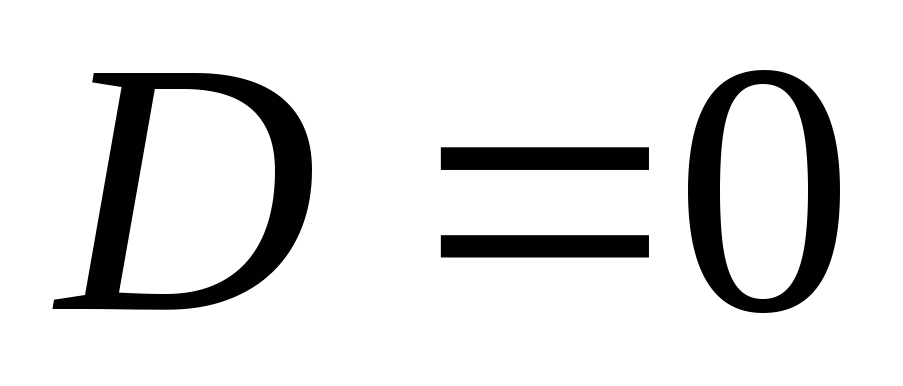 .
.
3) ศักย์ของสนามไฟฟ้าสถิตเป็นฟังก์ชันต่อเนื่องของพิกัด ดังนั้นจึงจำเป็นที่ 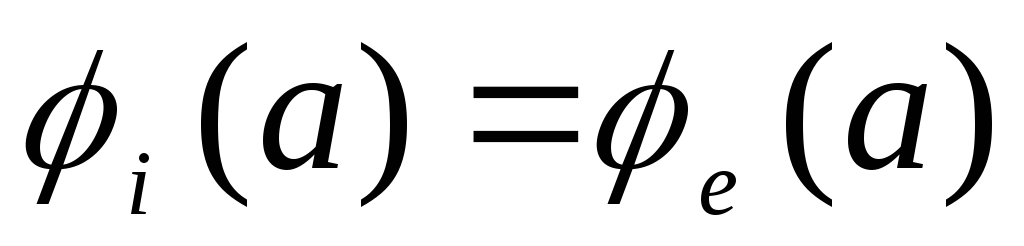 .
.
4) องค์ประกอบปกติของเวกเตอร์  ไม่ควรสัมผัสกับการกระโดดเมื่อผ่านพื้นผิวของลูกบอลเช่น
ไม่ควรสัมผัสกับการกระโดดเมื่อผ่านพื้นผิวของลูกบอลเช่น 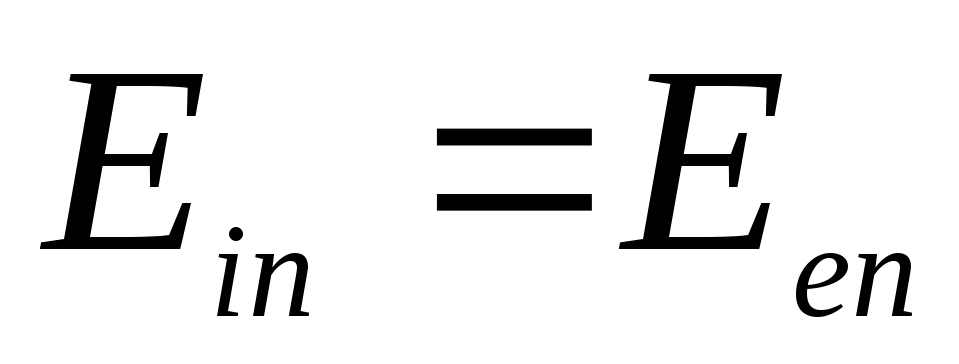 ที่
ที่ 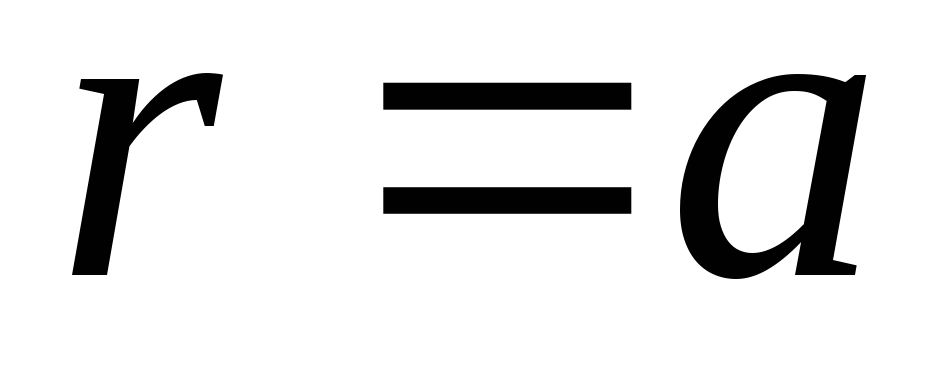 เนื่องจากความหนาแน่นประจุของพื้นผิวบนพื้นผิวของลูกบอลเป็นศูนย์ เงื่อนไขสุดท้ายเทียบเท่ากับข้อกำหนด
เนื่องจากความหนาแน่นประจุของพื้นผิวบนพื้นผิวของลูกบอลเป็นศูนย์ เงื่อนไขสุดท้ายเทียบเท่ากับข้อกำหนด
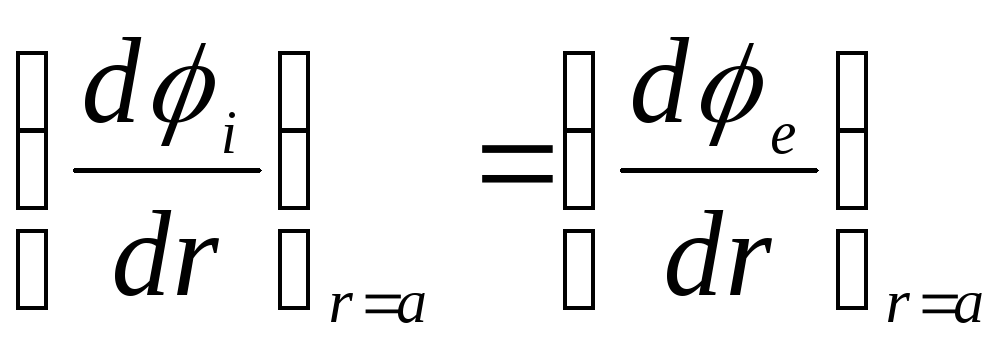 .
.
จากสองเงื่อนไขสุดท้ายที่เราพบ
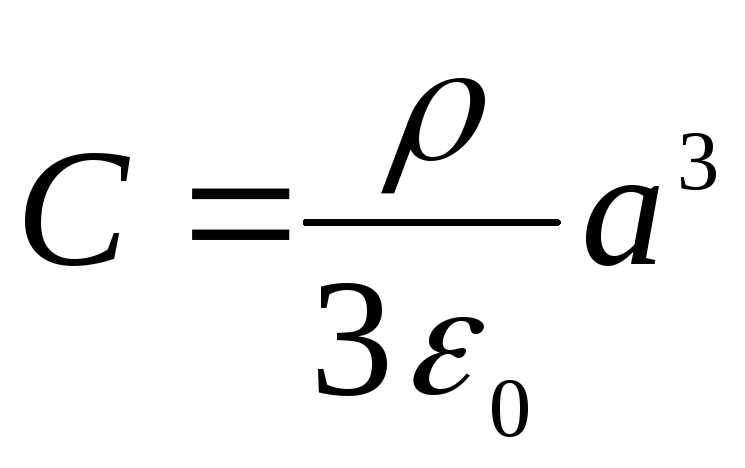 ,
,
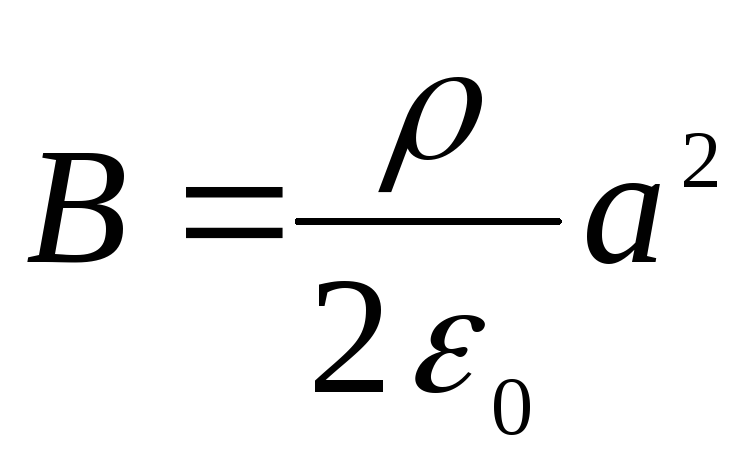 .
.
ในที่สุดเราก็เขียนศักยภาพที่ต้องการในรูปแบบ
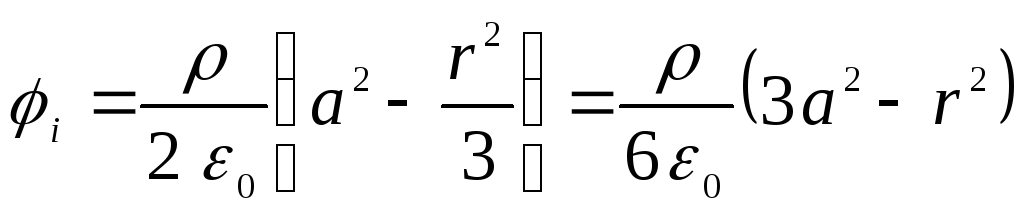 ,
,
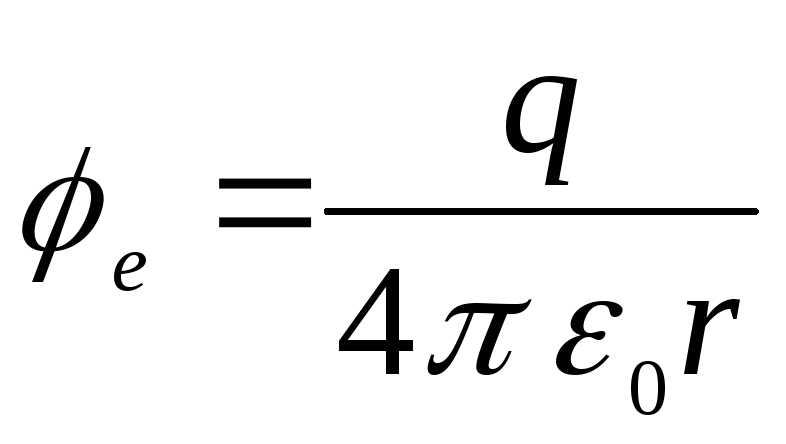 .
.
จากสูตรเหล่านี้จะเห็นได้ว่าศักยภาพภายนอกของลูกบอลนั้นคล้ายกับสนามของจุดชาร์จ
มาวาดกราฟกันเถอะ 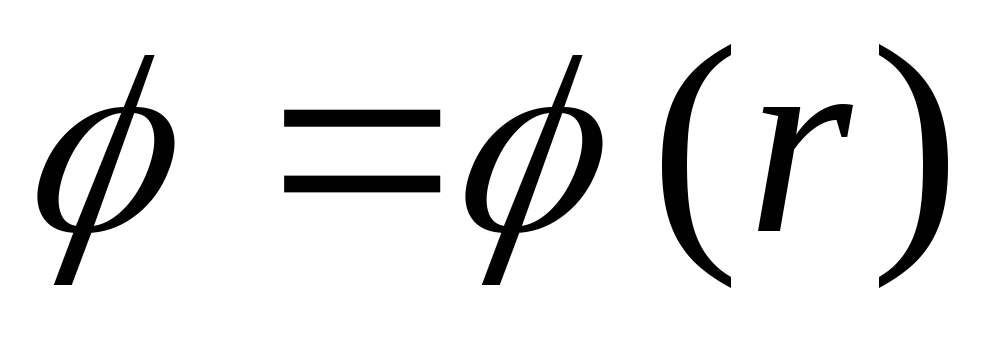 .
.
อนุญาต 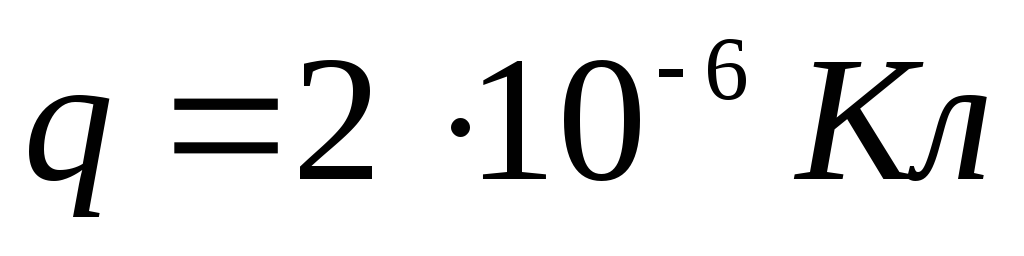 ,
,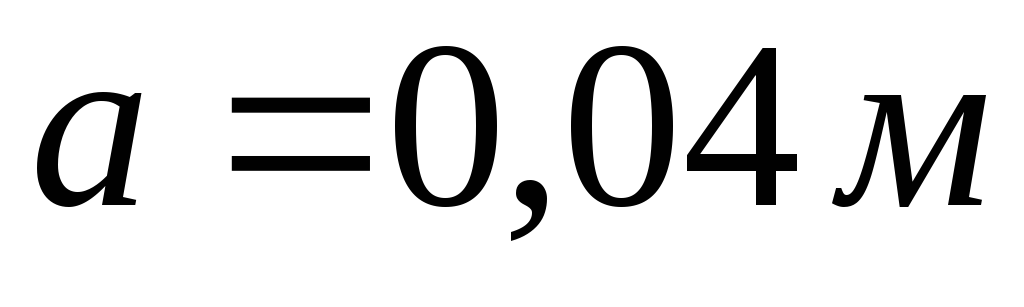 . มาหาความหนาแน่นของประจุกัน
. มาหาความหนาแน่นของประจุกัน
และทัศนคติ
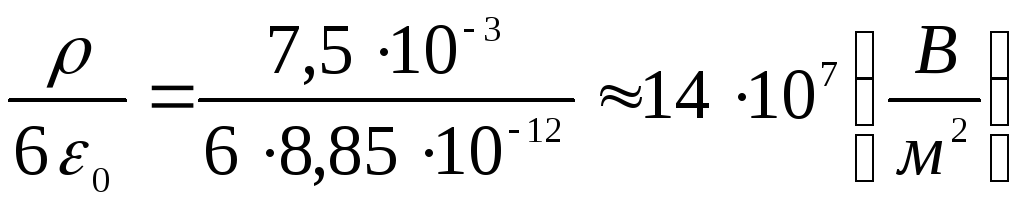 .
.
ตอนนี้เราสามารถเขียนว่าศักยภาพภายในทรงกลมได้
มาทำโต๊ะกันเถอะ
|
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ศักยภาพที่อยู่นอกขอบเขต 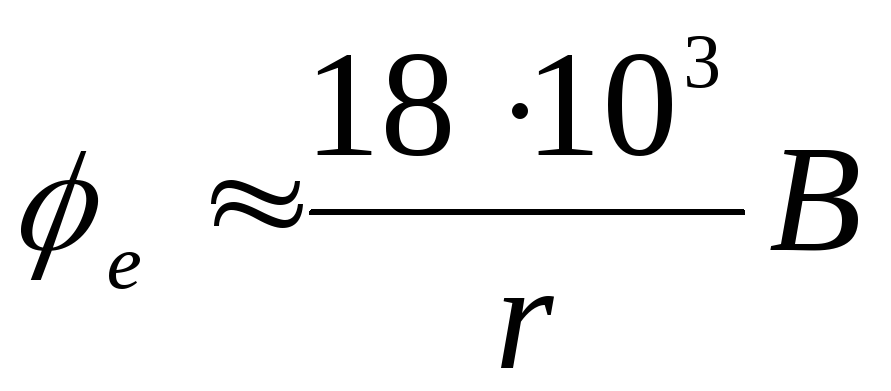 .
.
|
| |||||||
|
|
|
|
|
|
|
|
|
ตอนนี้เราสร้างกราฟ 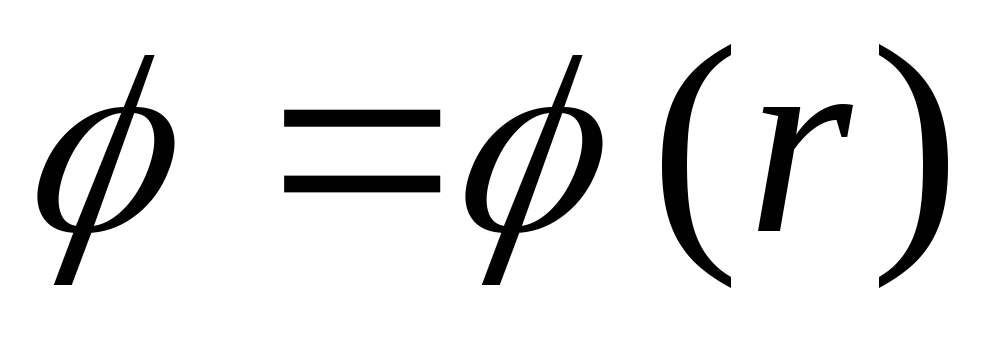 .
.
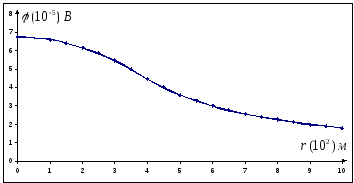
ความสัมพันธ์ระหว่างความตึงเครียดและศักยภาพ
การพึ่งพาความแรงของสนามไฟฟ้าสถิตในระยะถึงจุดศูนย์กลางของลูกบอลภายในลูกบอลมีรูปแบบ (ดูวิธีแก้ปัญหา 1.5.4)
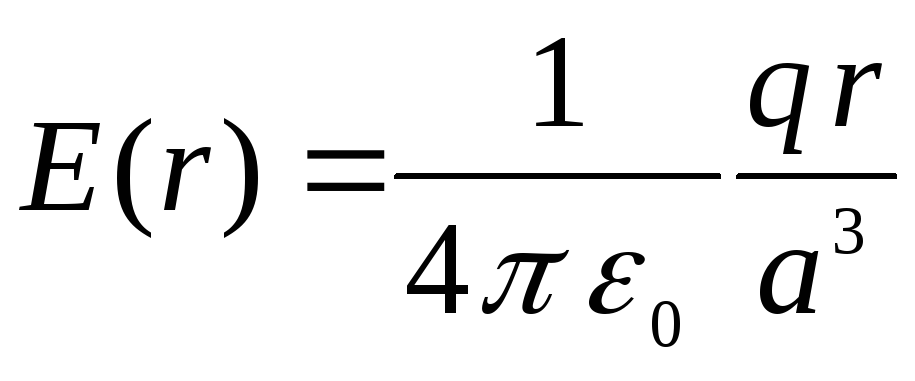 ,
,
เหล่านั้น. ภายในทรงกลม ความแรงของสนามจะเพิ่มขึ้นเป็นเส้นตรงตามระยะห่างจากจุดศูนย์กลาง ที่ 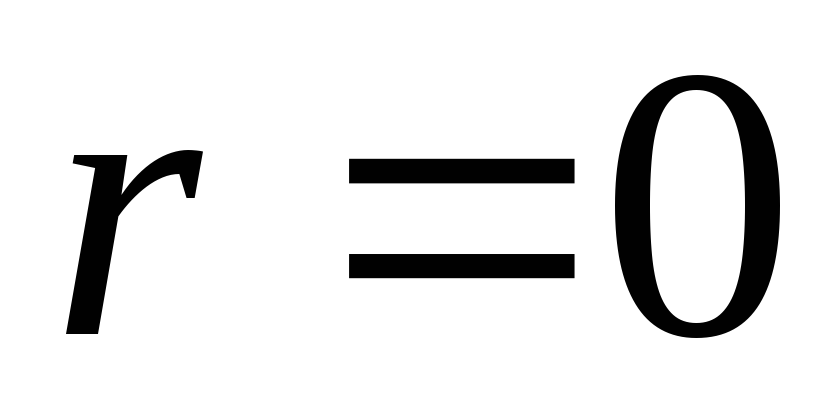 ,
,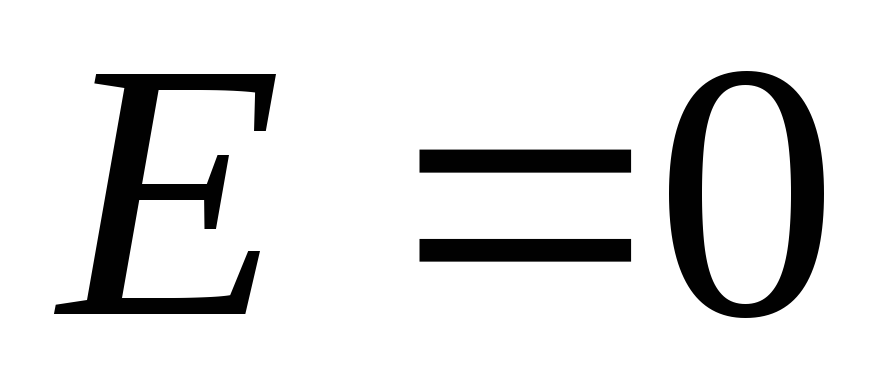 , ที่
, ที่ 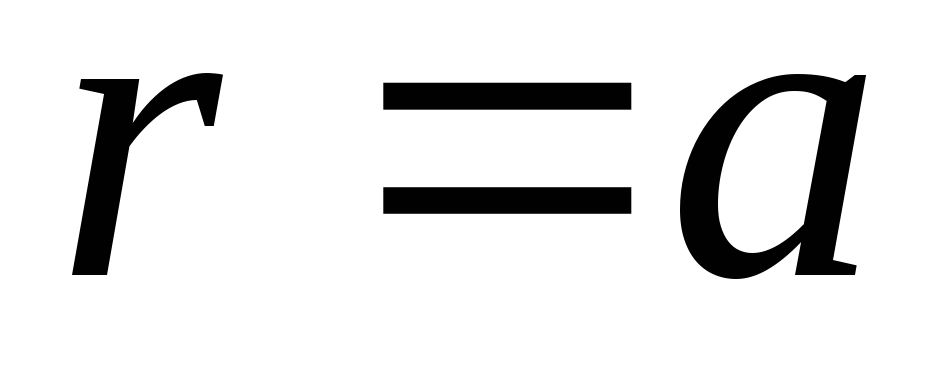 ถึงค่าสูงสุดและเท่ากับ
ถึงค่าสูงสุดและเท่ากับ
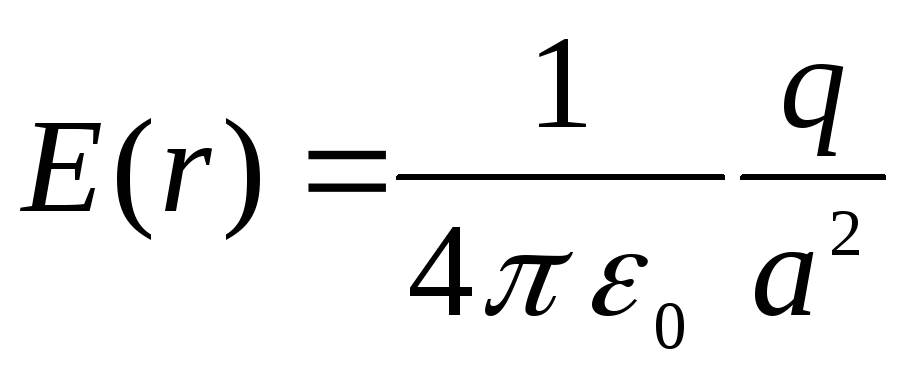 .
.
ที่  ความแรงของสนามขึ้นอยู่กับระยะทางเนื่องจากความแรงของสนามของประจุแบบจุด
ความแรงของสนามขึ้นอยู่กับระยะทางเนื่องจากความแรงของสนามของประจุแบบจุด
การเปลี่ยนแปลงที่อาจเกิดขึ้นในสนามของลูกบอลที่ถูกชาร์จ
ศักยภาพของสนามภายในลูกบอล
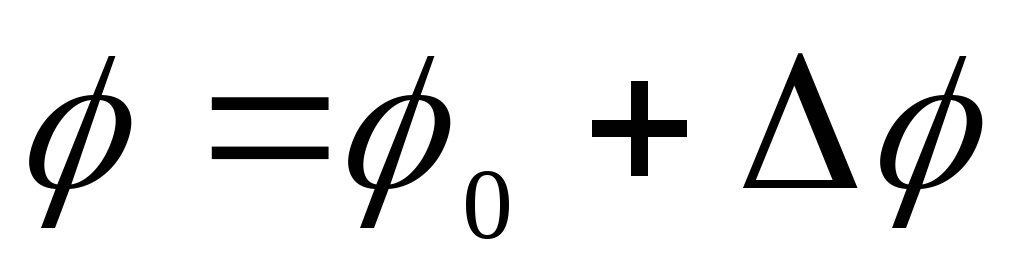 ,
,
ที่ไหน 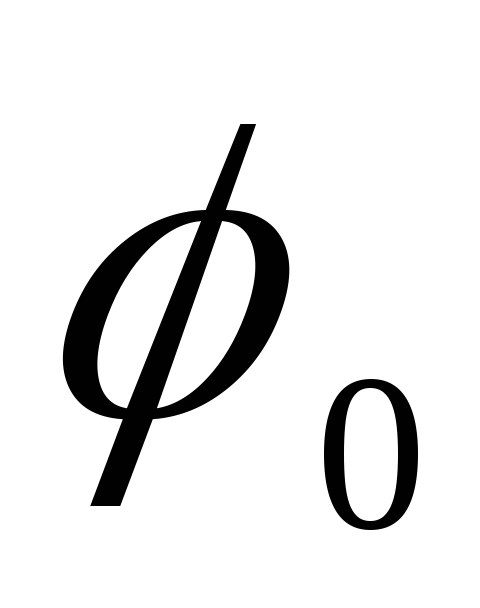 คือ ค่าศักย์ของจุดบนผิวลูก (ศักย์สนามของจุดพุ่ง) เท่ากับ
คือ ค่าศักย์ของจุดบนผิวลูก (ศักย์สนามของจุดพุ่ง) เท่ากับ
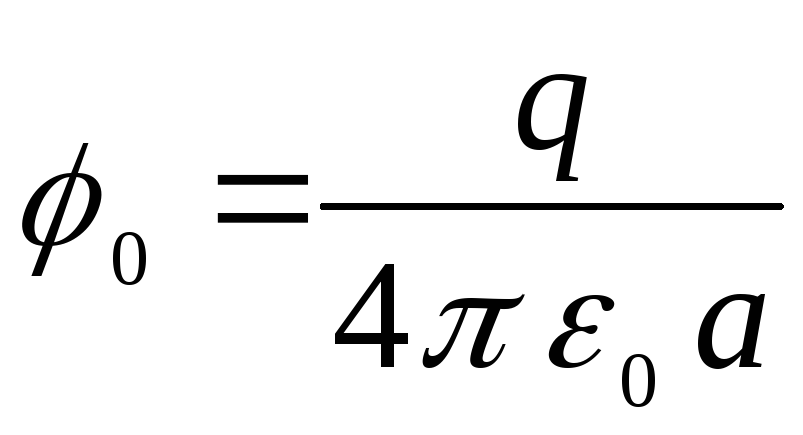 .
.
ในที่สุดเราก็ได้
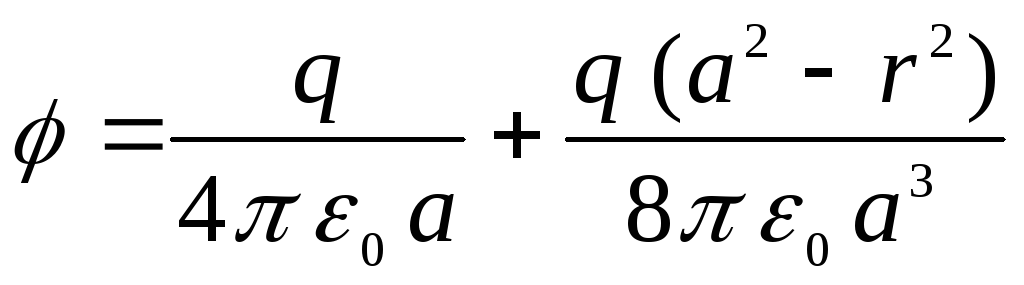 .
.
พิจารณาว่าความหนาแน่นของประจุจำนวนมาก
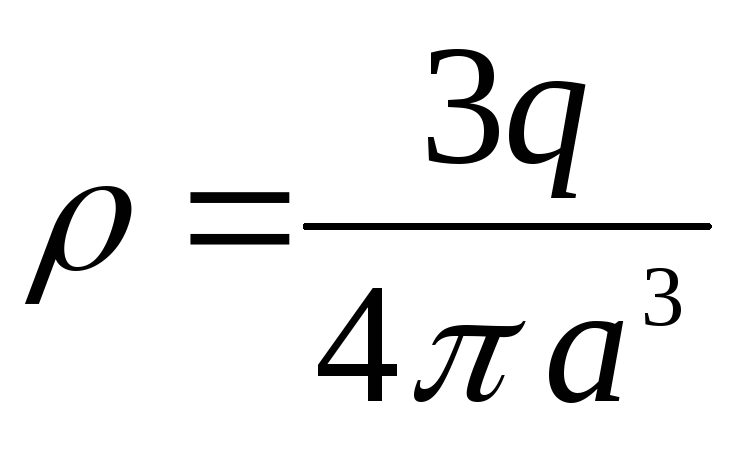 ,
,
เขียนได้
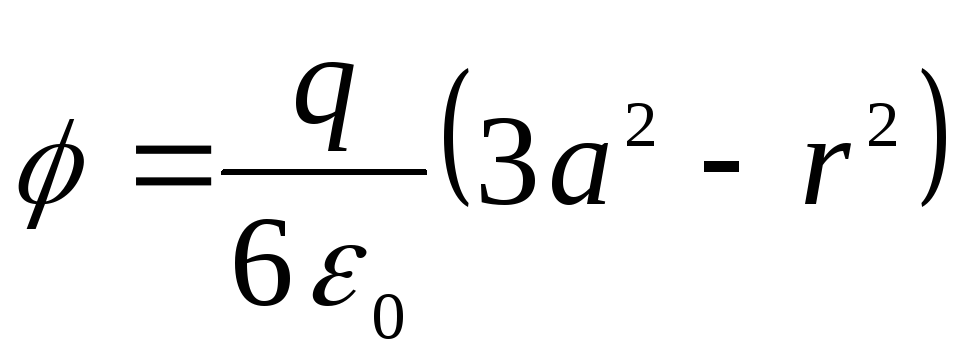 ,
,
เหล่านั้น. เรามาอยู่ในสูตรเดียวกับการแก้ปัญหาโดยการรวมสมการปัวซองเข้าไว้ด้วยกัน
1.7.6. ศักยภาพของสนามผลลัพธ์ที่จุด A
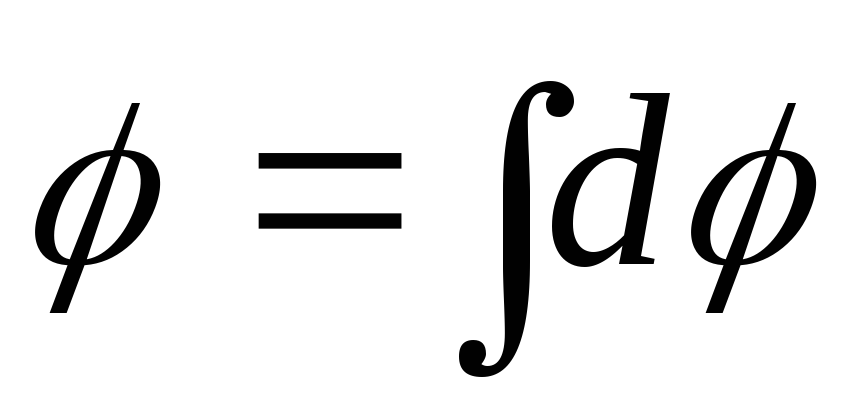 ,
,
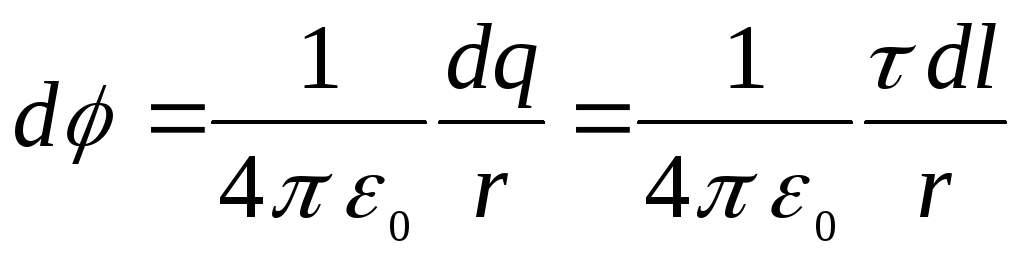
คือศักยภาพของสนามที่สร้างขึ้นโดยประจุ 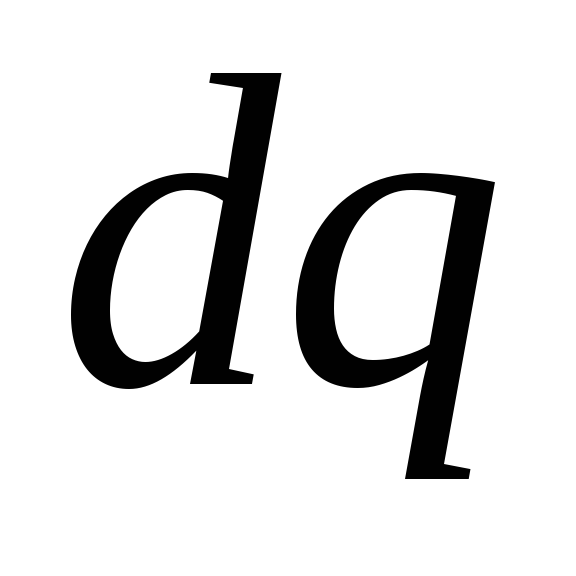 องค์ประกอบแหวน
องค์ประกอบแหวน  .
.
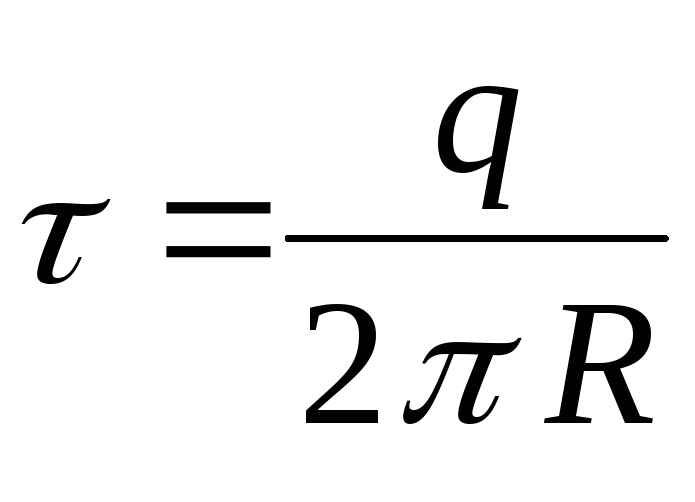
คือความหนาแน่นประจุเชิงเส้น r คือระยะห่างจากองค์ประกอบ  ไปยังจุดที่กำหนด จากสองสูตรสุดท้ายที่เรามี
ไปยังจุดที่กำหนด จากสองสูตรสุดท้ายที่เรามี
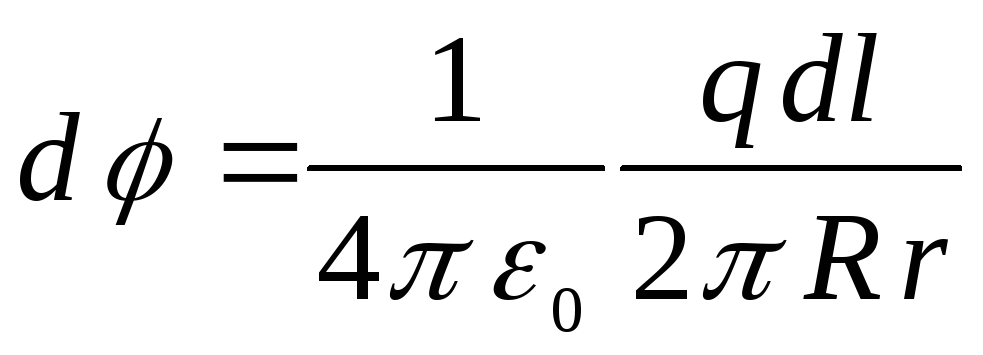 .
.
ผลลัพธ์ที่เป็นไปได้
จากการพิจารณาทางเรขาคณิต จะได้ว่า
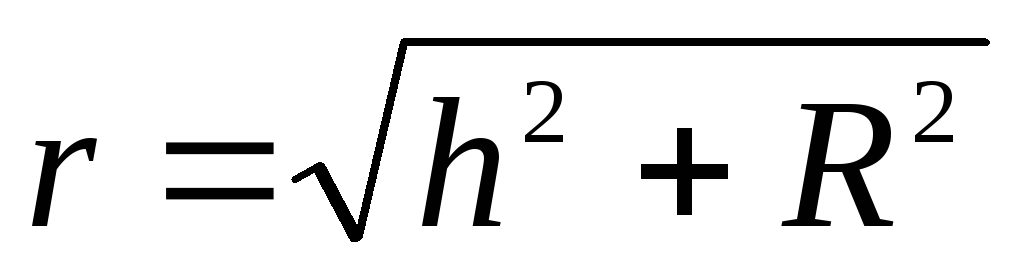 .
.
เพราะเหตุนี้,
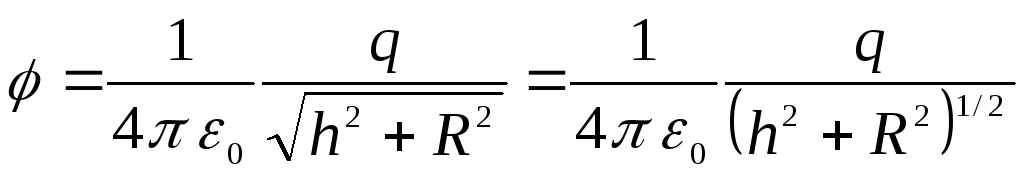 .
.
ความแรงของสนาม
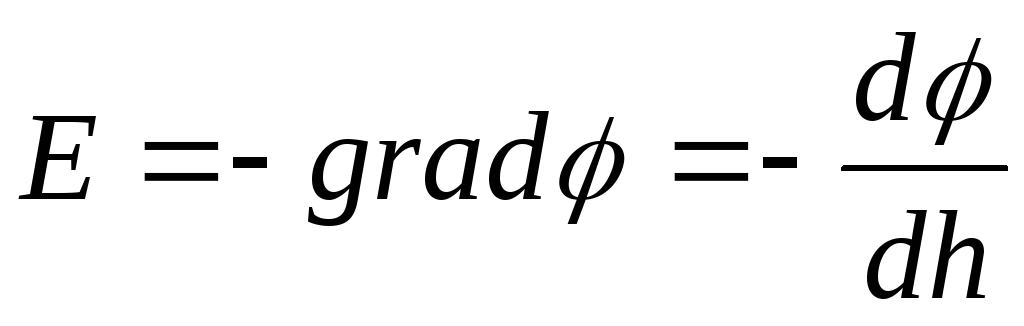 .
.
การแยกวิเคราะห์นิพจน์ 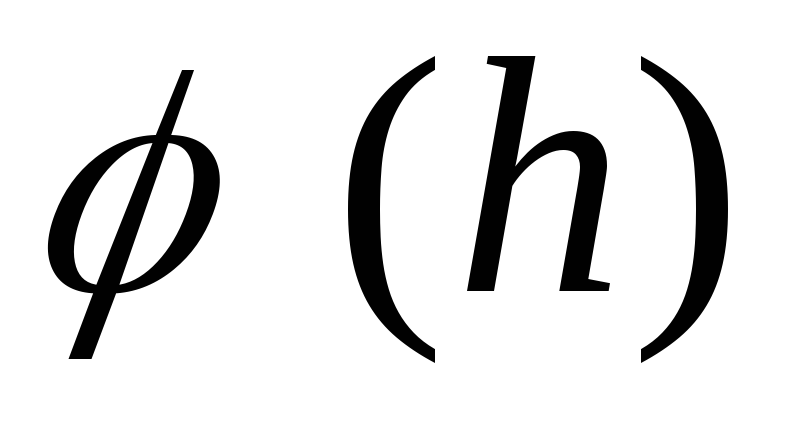 และ
และ ![]() แสดงว่าอยู่ตรงกลางวงแหวน (
แสดงว่าอยู่ตรงกลางวงแหวน ( 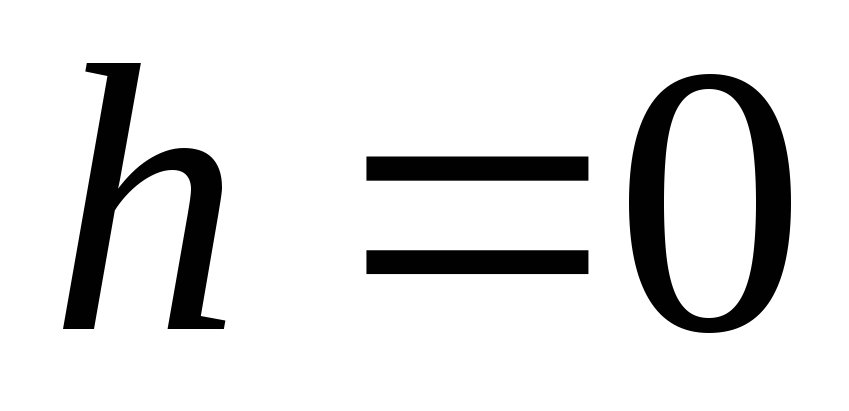 ) ศักยภาพมีค่าสูงสุด และความแรงของสนามจะหายไป
) ศักยภาพมีค่าสูงสุด และความแรงของสนามจะหายไป
ที่ 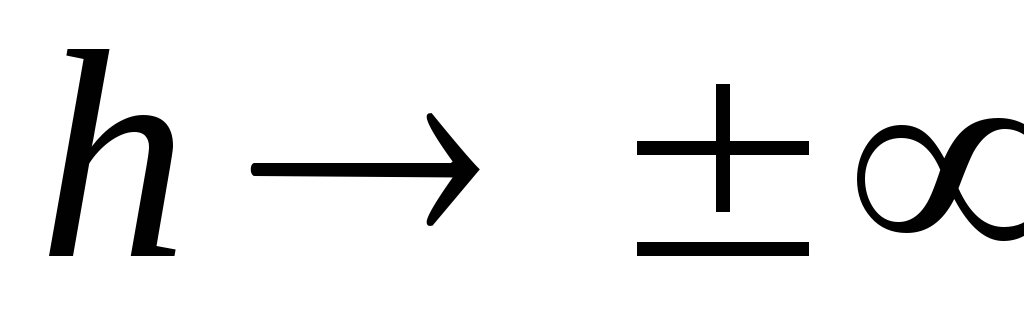 ทั้งศักยภาพและความตึงเครียดมักจะเป็นศูนย์
ทั้งศักยภาพและความตึงเครียดมักจะเป็นศูนย์
ที่ 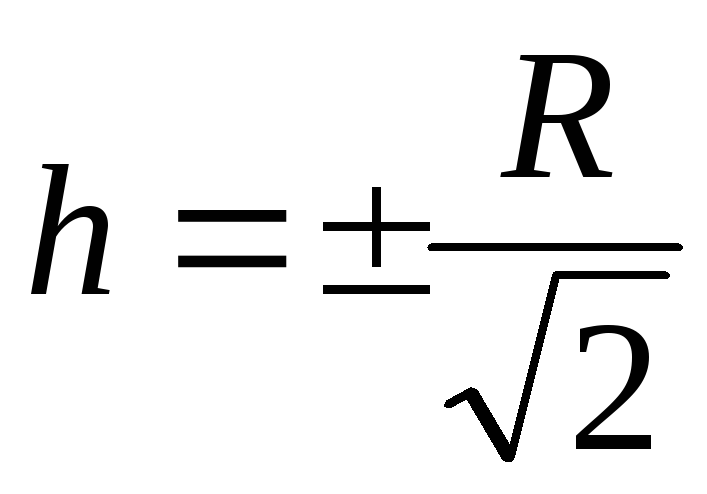 อนุพันธ์
อนุพันธ์ 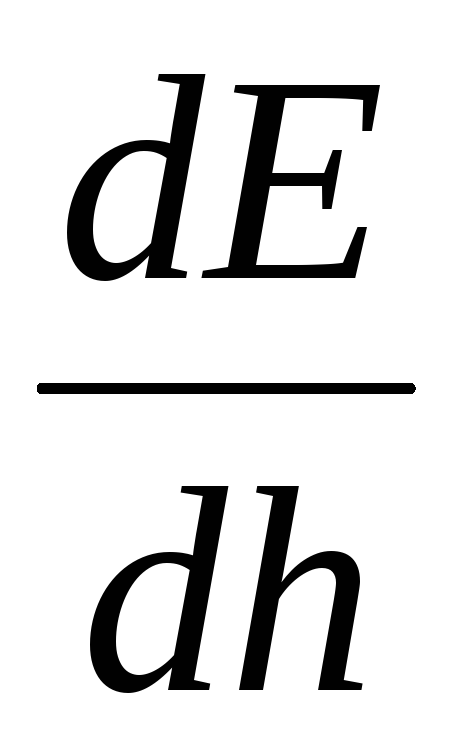 หายไปดังนั้น ณ จุดนี้ความแรงของสนามสูงสุดและบนกราฟ
หายไปดังนั้น ณ จุดนี้ความแรงของสนามสูงสุดและบนกราฟ 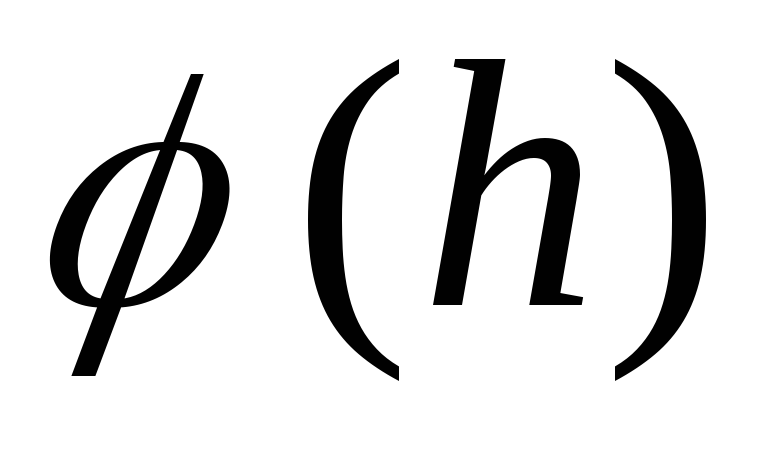 (ดูรูปที่ ____) จะมีจุดเปลี่ยน กำหนดการ
(ดูรูปที่ ____) จะมีจุดเปลี่ยน กำหนดการ ![]() ตั้งอยู่ในไตรมาสที่ 1 และ 3 เช่น
ตั้งอยู่ในไตรมาสที่ 1 และ 3 เช่น 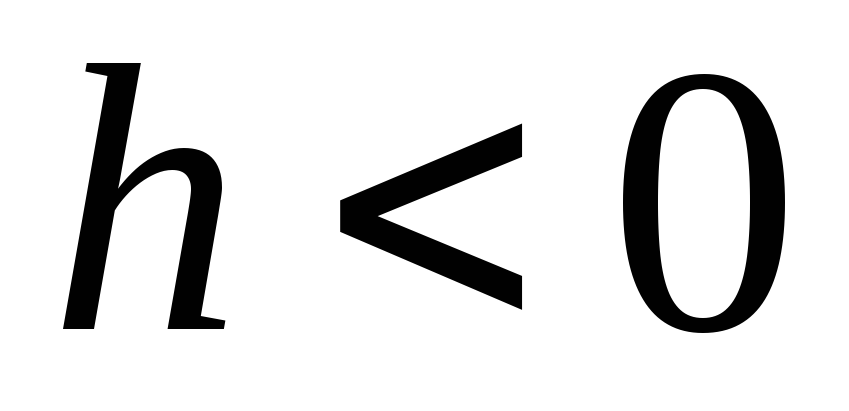 ,
,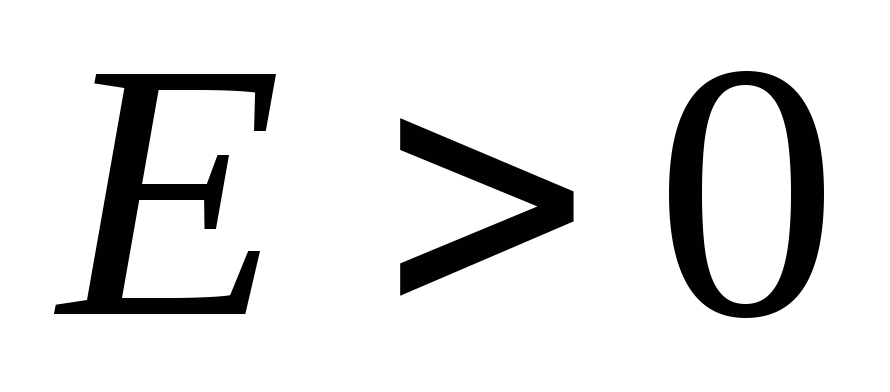 . ซึ่งหมายความว่าเมื่อผ่านศูนย์กลางของวงแหวน (
. ซึ่งหมายความว่าเมื่อผ่านศูนย์กลางของวงแหวน ( 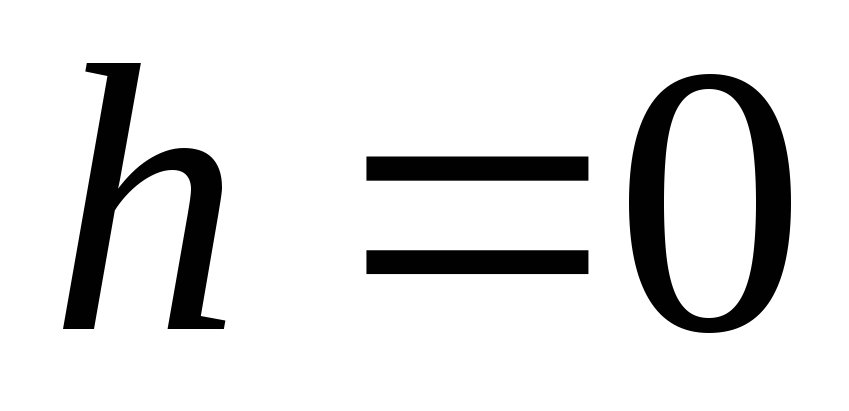 ) เวกเตอร์
) เวกเตอร์  เปลี่ยนทิศทางไปในทางตรงข้าม
เปลี่ยนทิศทางไปในทางตรงข้าม
กำหนดการ 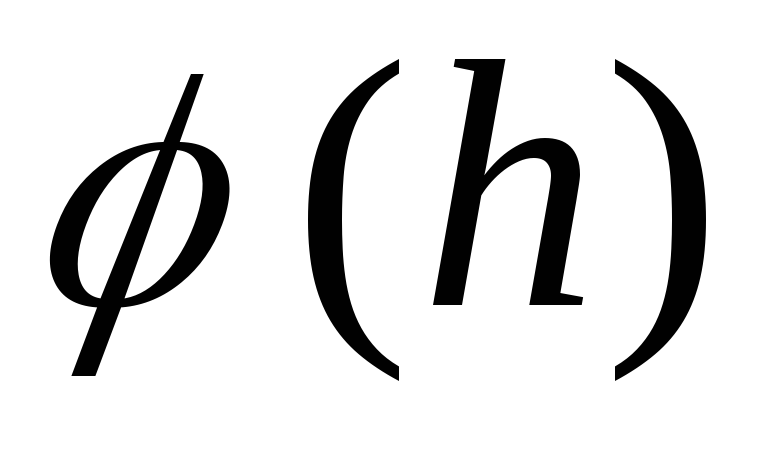 ตั้งอยู่ในไตรมาสที่ 1 และ 2 คือ ทั้งสองด้านของวงแหวนตรงจุดที่อยู่บนแกนของวงแหวน ค่าศักย์ไฟฟ้าเป็นบวก
ตั้งอยู่ในไตรมาสที่ 1 และ 2 คือ ทั้งสองด้านของวงแหวนตรงจุดที่อยู่บนแกนของวงแหวน ค่าศักย์ไฟฟ้าเป็นบวก
โดยใช้ตัวอย่างของการแก้ปัญหานี้ เราสามารถมั่นใจได้ว่าเมื่อการอ้างอิงที่เป็นไปได้เปลี่ยนไป ความต่างศักย์ระหว่างจุดสองจุดใดๆ จะไม่เปลี่ยนแปลง ลักษณะทั้งหมดของการพึ่งพาศักยภาพในระยะทางจะไม่เปลี่ยนแปลงเช่นกัน ตัวอย่างเช่น หากคุณเลือกจุดเริ่มต้นที่อยู่ตรงกลางของวงแหวน นั่นคือ สมมติว่า 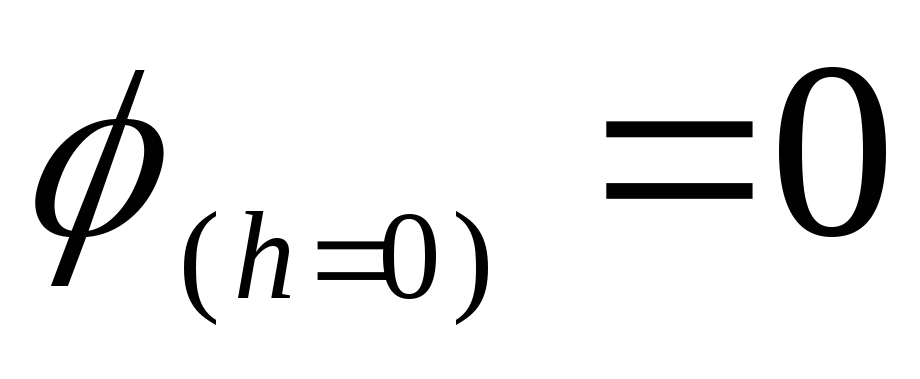 ดังนั้นศักย์ของจุดใดๆ ที่วางอยู่บนแกนของวงแหวนจะเท่ากับ
ดังนั้นศักย์ของจุดใดๆ ที่วางอยู่บนแกนของวงแหวนจะเท่ากับ
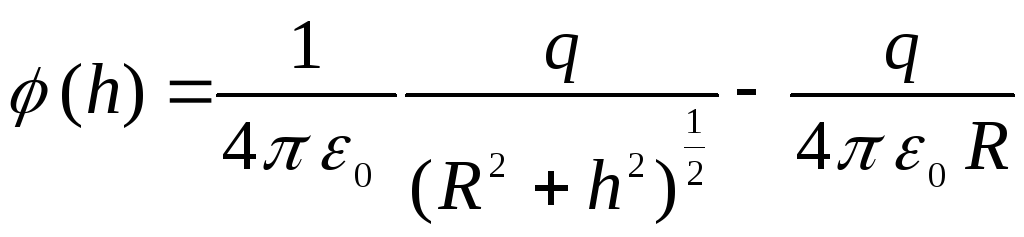 .
.
สูตรนี้สามารถหาได้ง่ายโดยอาศัยหลักการทับซ้อน
หากเลือกจุดกำเนิดของศักย์ที่ศูนย์กลางของวงแหวน แสดงว่าศักยภาพของสนามที่สร้างขึ้นโดยประจุพื้นฐาน 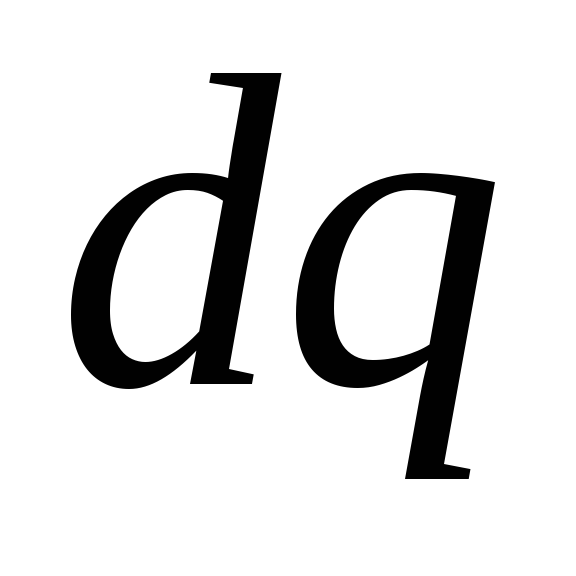 ที่จุด A สามารถแสดงเป็น
ที่จุด A สามารถแสดงเป็น
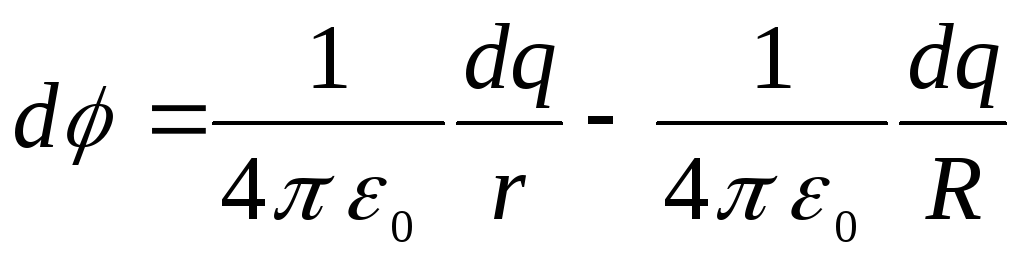 .
.
เมื่อรวมนิพจน์นี้เข้ากับวงแหวนทั้งหมด เราจะได้สูตร
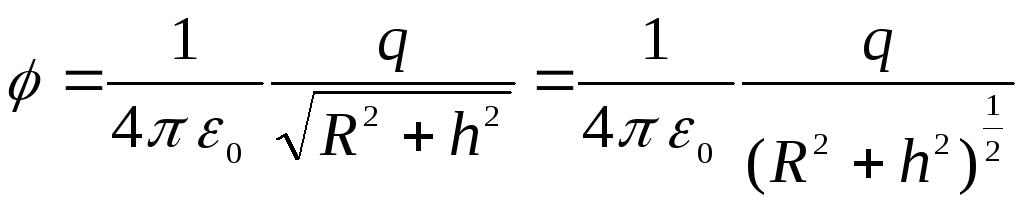 .
.
กราฟการพึ่งพา 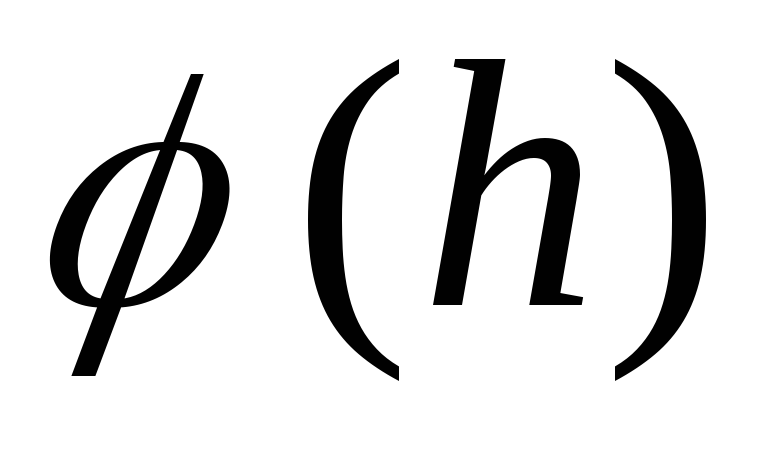 โดยไม่ต้องเปลี่ยนอักขระ เลื่อนลงขนานกับตัวเองตามจำนวน
โดยไม่ต้องเปลี่ยนอักขระ เลื่อนลงขนานกับตัวเองตามจำนวน 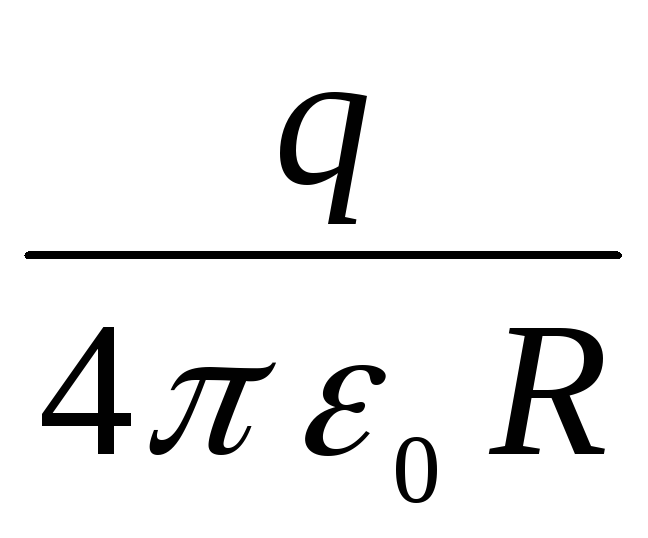 (เส้นประในรูป _____2) ที่
(เส้นประในรูป _____2) ที่ 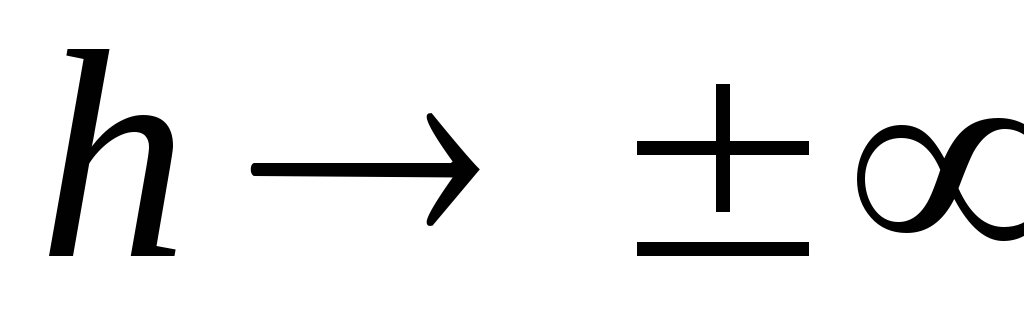 ศักยภาพมีแนวโน้มที่จะให้คุณค่า
ศักยภาพมีแนวโน้มที่จะให้คุณค่า 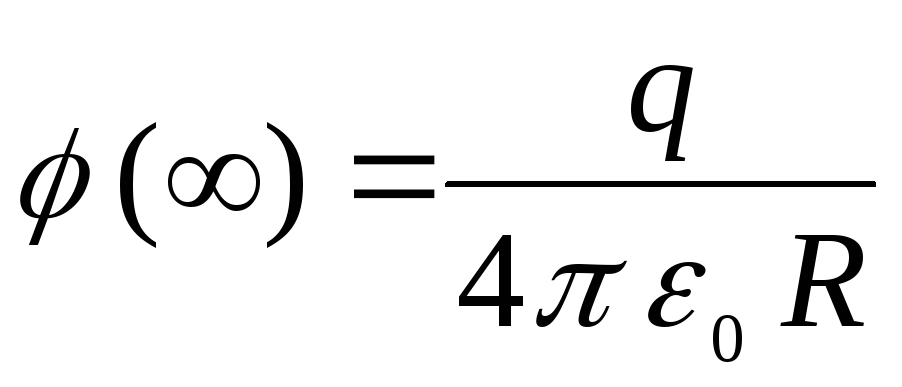 .
.
7.7. ศักยภาพเชิงตัวเลข เท่ากับงานดำเนินการโดยแรงของสนามไฟฟ้าเมื่อเคลื่อนที่ประจุบวกของหน่วยจากจุดที่กำหนดของสนาม
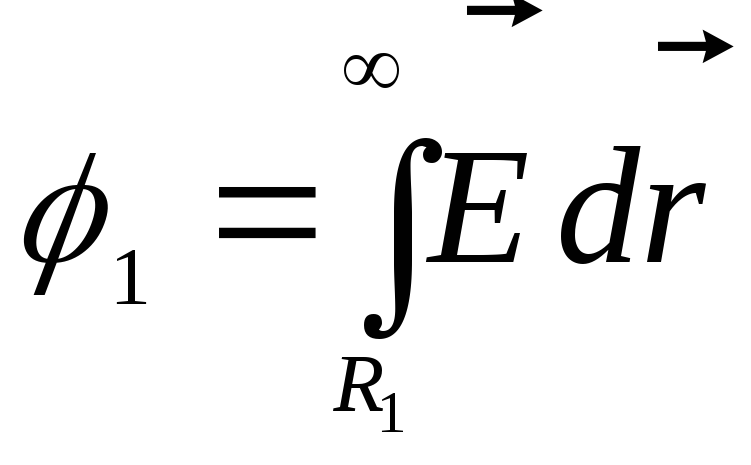 ,
,
ที่ไหน  คือความแรงของสนามที่เกิดในทุกจุดของช่วงการรวม
คือความแรงของสนามที่เกิดในทุกจุดของช่วงการรวม
ในช่วงเวลา 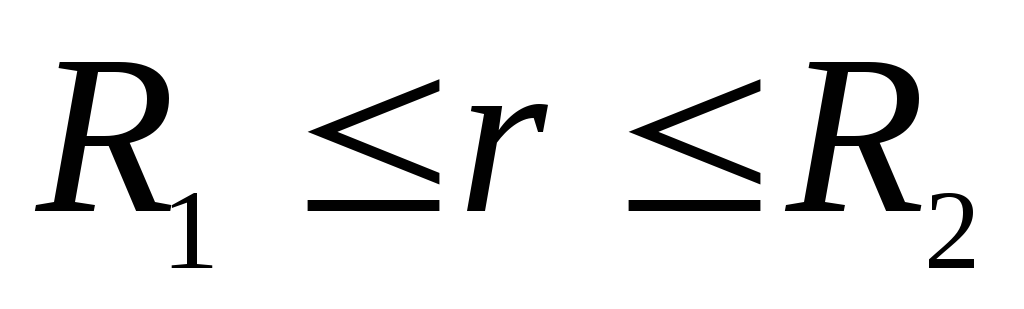 สนามถูกสร้างขึ้นโดยประจุของทรงกลมภายในเท่านั้น เวกเตอร์
สนามถูกสร้างขึ้นโดยประจุของทรงกลมภายในเท่านั้น เวกเตอร์  โดยไม่คำนึงถึงขนาดและเครื่องหมายของประจุ
โดยไม่คำนึงถึงขนาดและเครื่องหมายของประจุ 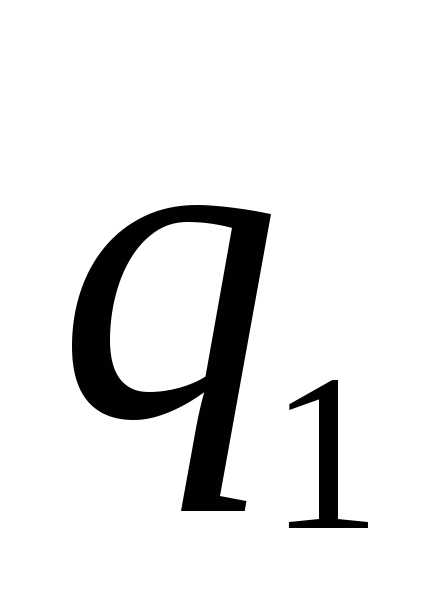 ชี้ไปตามรัศมีจากจุดศูนย์กลาง เมื่อย้ายประจุบวกหน่วยจาก
ชี้ไปตามรัศมีจากจุดศูนย์กลาง เมื่อย้ายประจุบวกหน่วยจาก  ก่อน
ก่อน 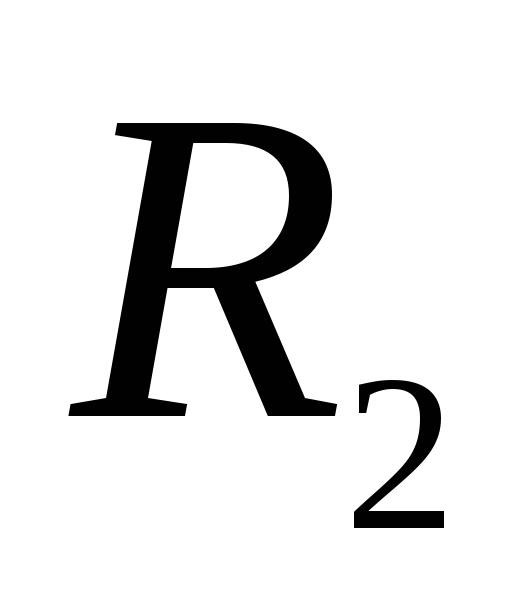 กองกำลังภาคสนามทำงานในเชิงบวก ที่
กองกำลังภาคสนามทำงานในเชิงบวก ที่ 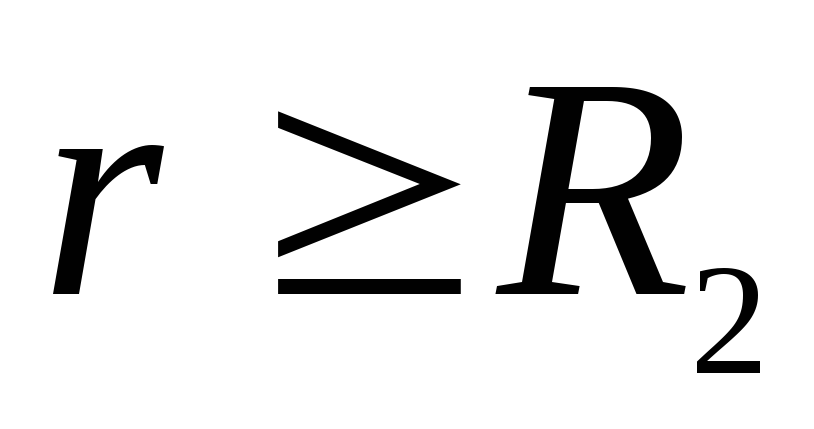 , เช่น. นอกทรงกลมที่สอง การทำงานของกองกำลังภาคสนามเป็นลบ ดังนั้น เวกเตอร์
, เช่น. นอกทรงกลมที่สอง การทำงานของกองกำลังภาคสนามเป็นลบ ดังนั้น เวกเตอร์  ชี้ไปตามรัศมีไปยังจุดศูนย์กลางของทรงกลม ณ จุด
ชี้ไปตามรัศมีไปยังจุดศูนย์กลางของทรงกลม ณ จุด 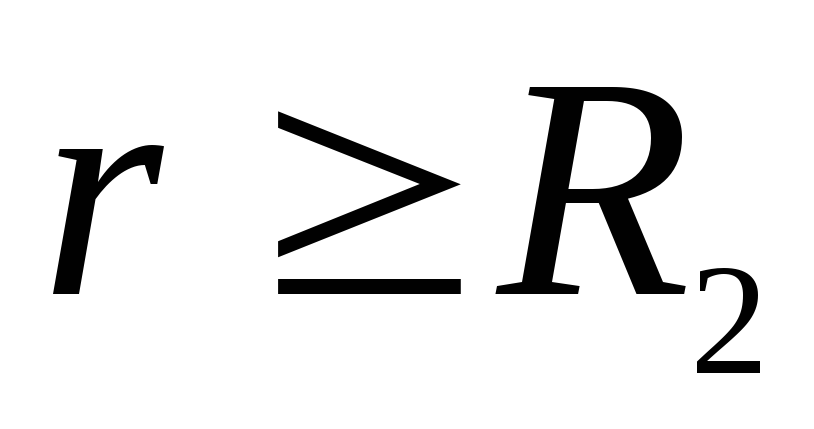 สนามถูกกำหนดโดยผลรวมเชิงพีชคณิตของประจุบนทรงกลมทั้งสอง ค่าใช้จ่าย
สนามถูกกำหนดโดยผลรวมเชิงพีชคณิตของประจุบนทรงกลมทั้งสอง ค่าใช้จ่าย 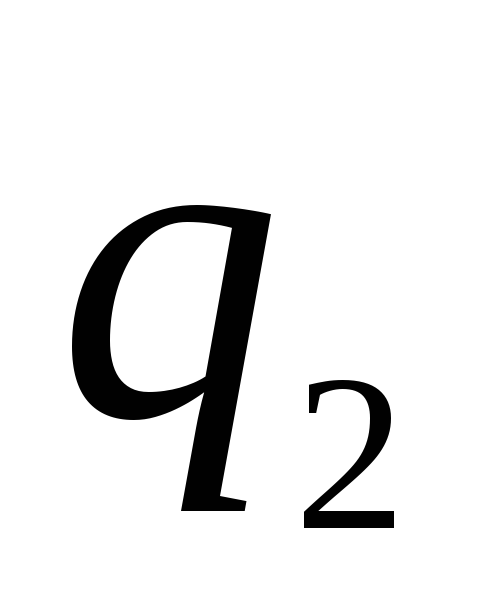 ต้องเป็นค่าลบและต้องมากกว่าประจุ
ต้องเป็นค่าลบและต้องมากกว่าประจุ 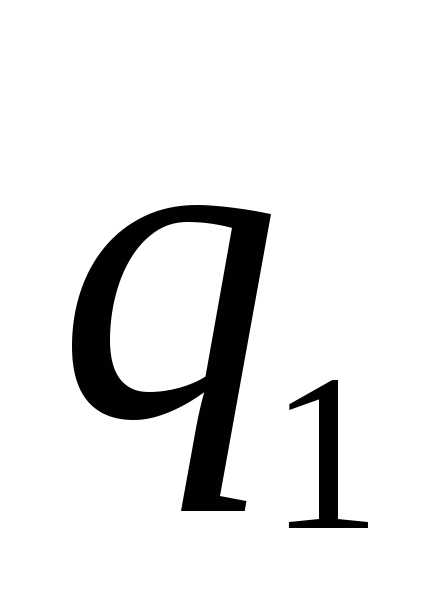 . เนื่องจากเวกเตอร์
. เนื่องจากเวกเตอร์  และ
และ 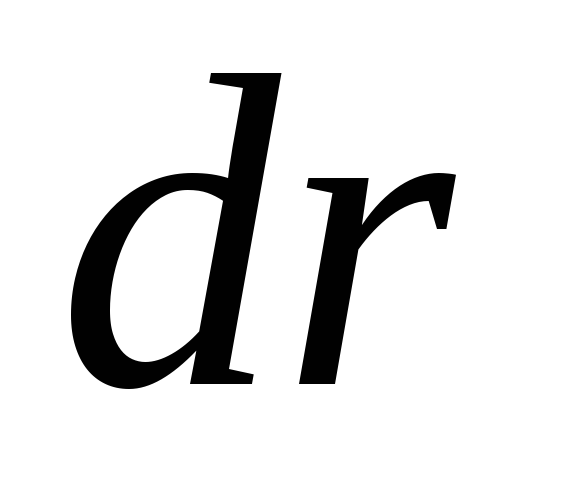 collinear (หรือ anticolinear if
collinear (หรือ anticolinear if 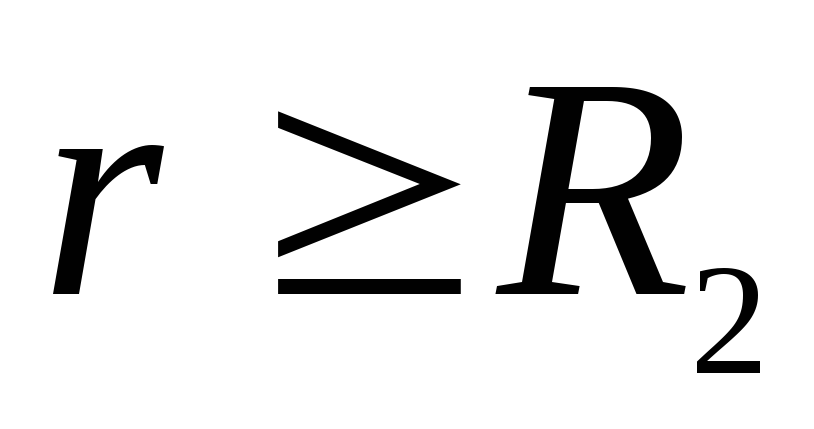 ) แล้วผลคูณสเกลาร์
) แล้วผลคูณสเกลาร์ ![]() สามารถแทนที่ด้วย
สามารถแทนที่ด้วย 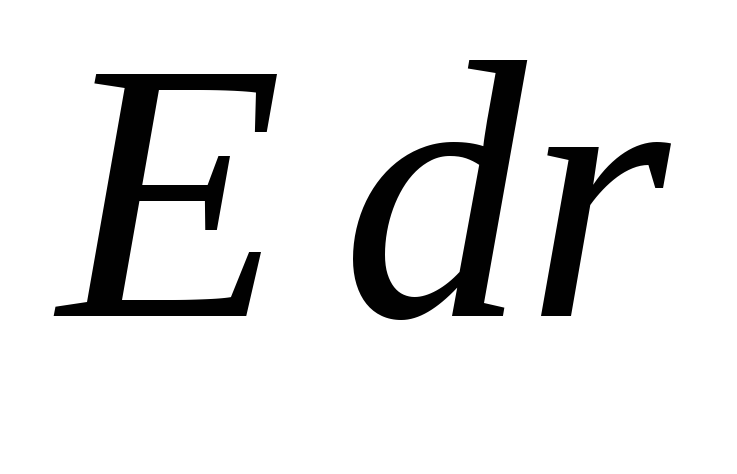 (ในกรณีที่เวกเตอร์ทั้งสองนี้มีทิศทางตรงกันข้าม ควรพิจารณาความแรงของสนามเป็นลบ) ในสูตร
(ในกรณีที่เวกเตอร์ทั้งสองนี้มีทิศทางตรงกันข้าม ควรพิจารณาความแรงของสนามเป็นลบ) ในสูตร 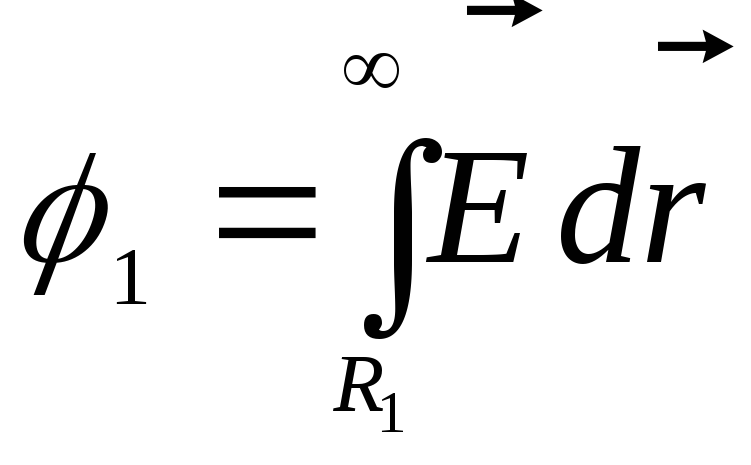 integrand
integrand 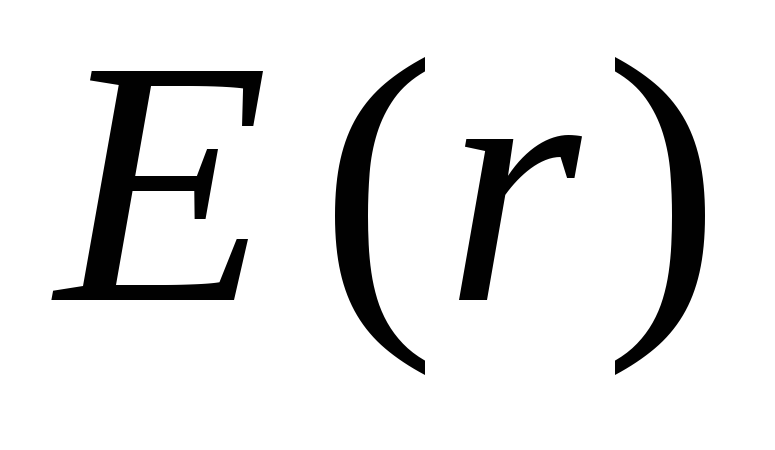 แตกในจุดหนึ่ง
แตกในจุดหนึ่ง 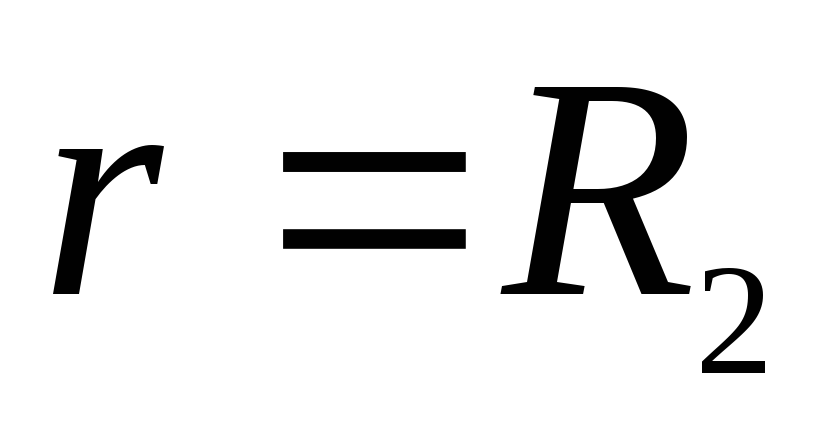 . ดังนั้นอินทิกรัลต้องแบ่งออกเป็นสองอินทิกรัลตั้งแต่
. ดังนั้นอินทิกรัลต้องแบ่งออกเป็นสองอินทิกรัลตั้งแต่  ก่อน
ก่อน 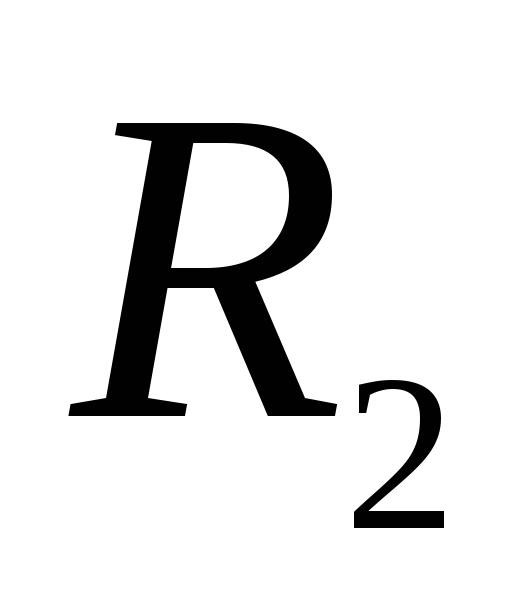 และจาก
และจาก 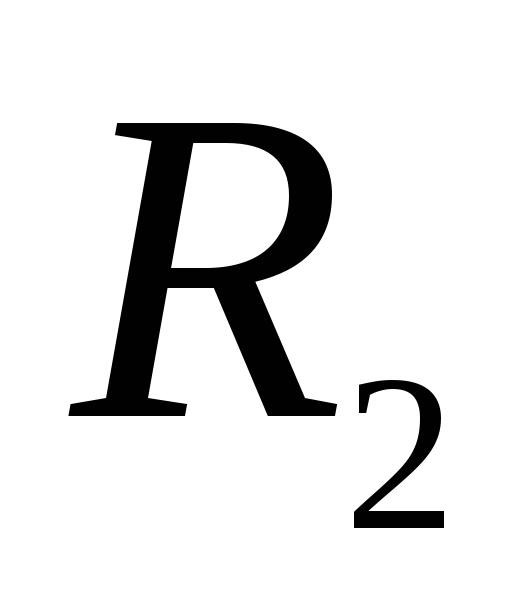 ก่อน
ก่อน  :
:
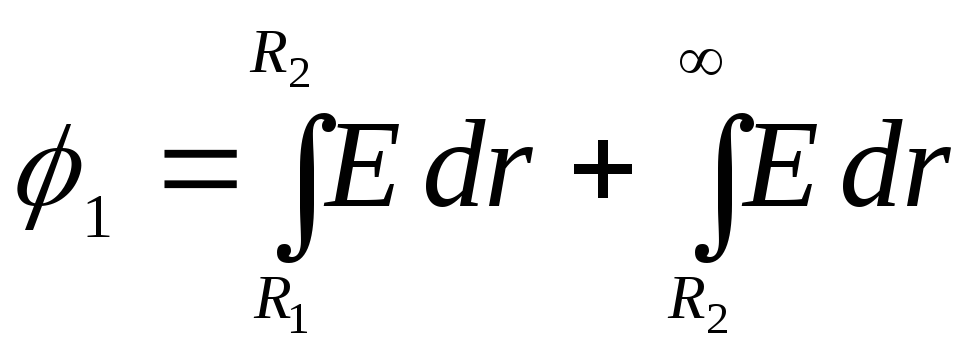 .
.
ที่ 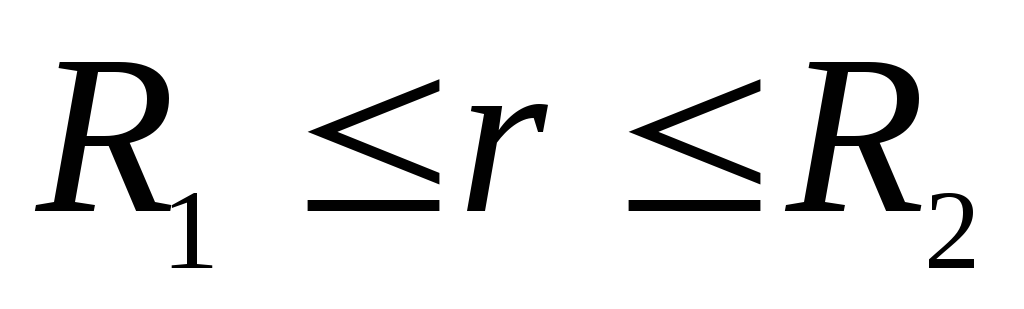 ความเครียด
ความเครียด
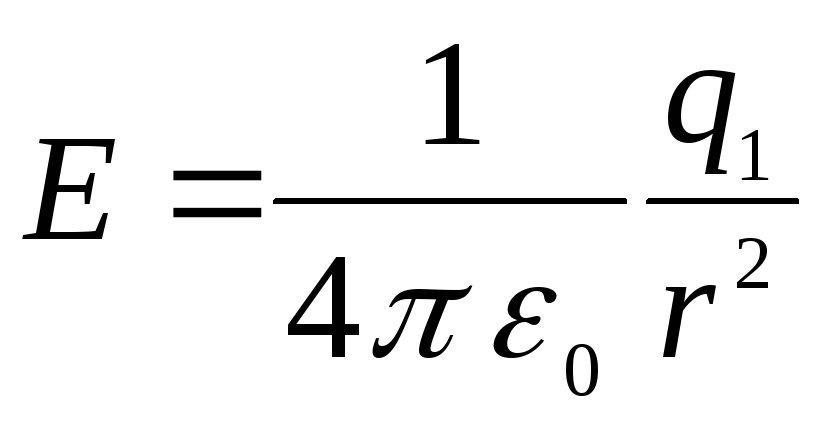 ,
,
และที่ 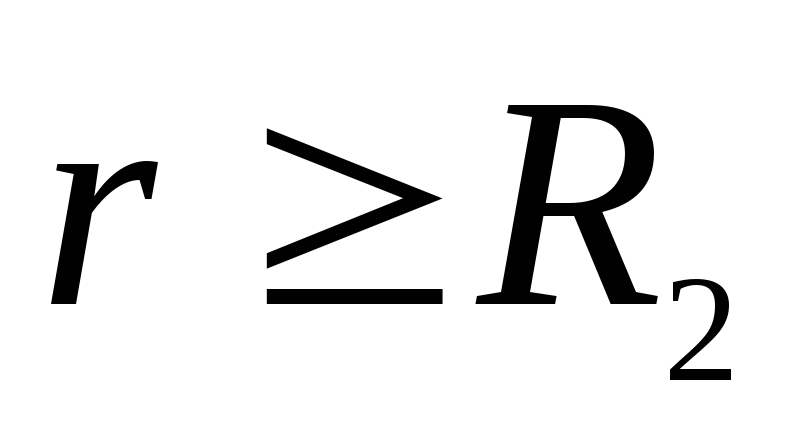
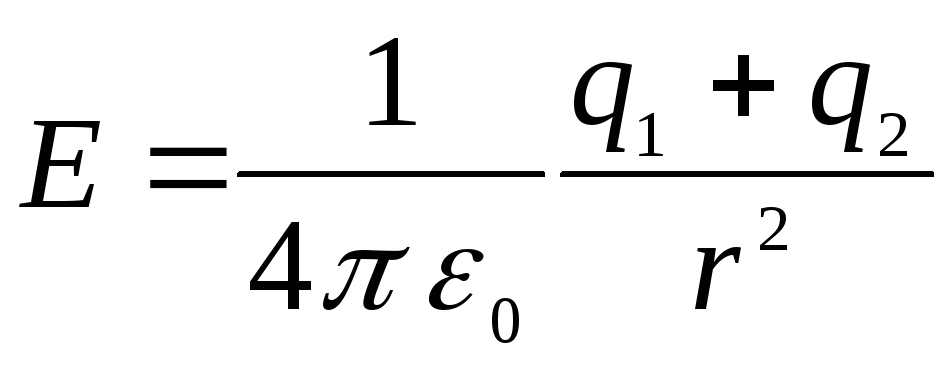 .
.
แทนนิพจน์เหล่านี้เป็นอินทิกรัลที่สอดคล้องกัน เราได้รับ
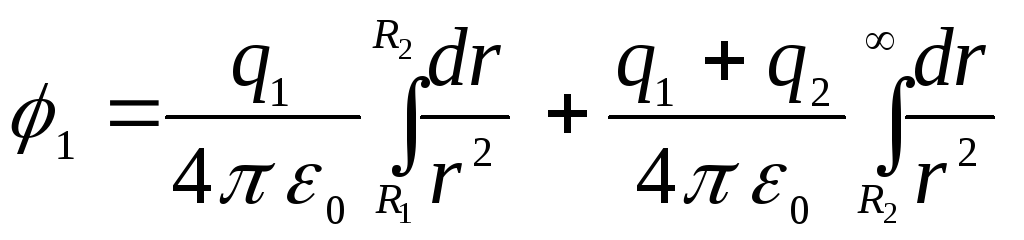 .
.
บูรณาการและลดเงื่อนไขเหมือนเราได้รับ
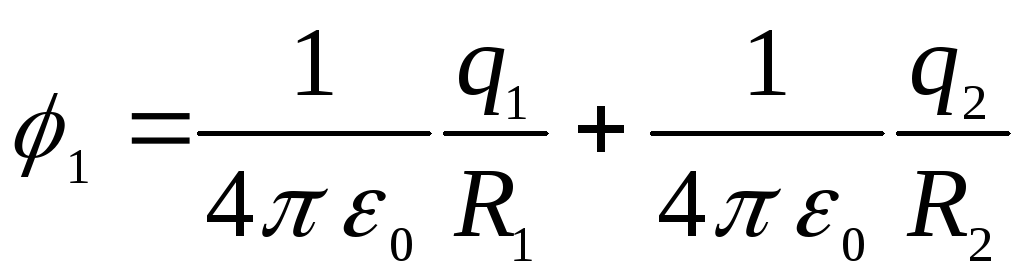 .
.
เนื่องจากตามสภาพของปัญหา 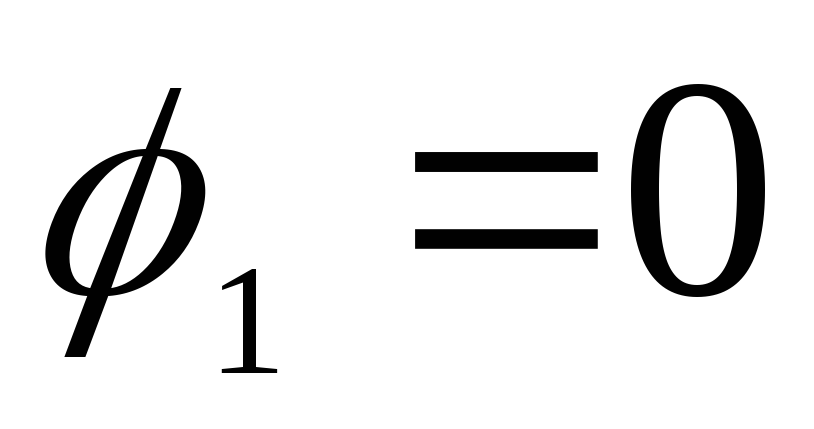 , แล้ว
, แล้ว
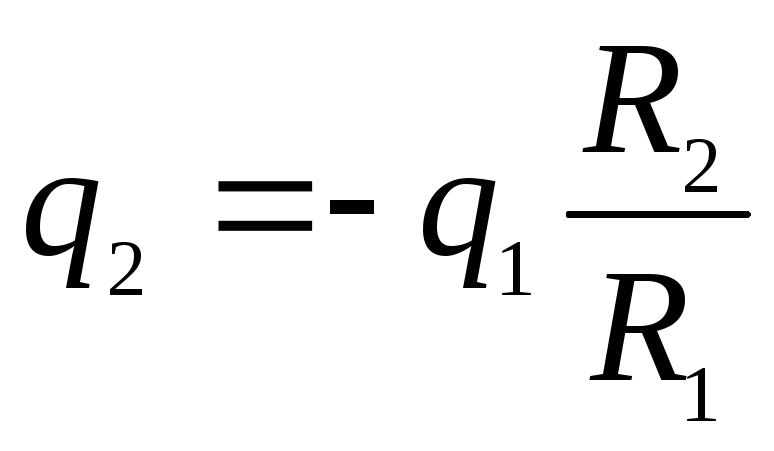 .
.
กราฟการพึ่งพา 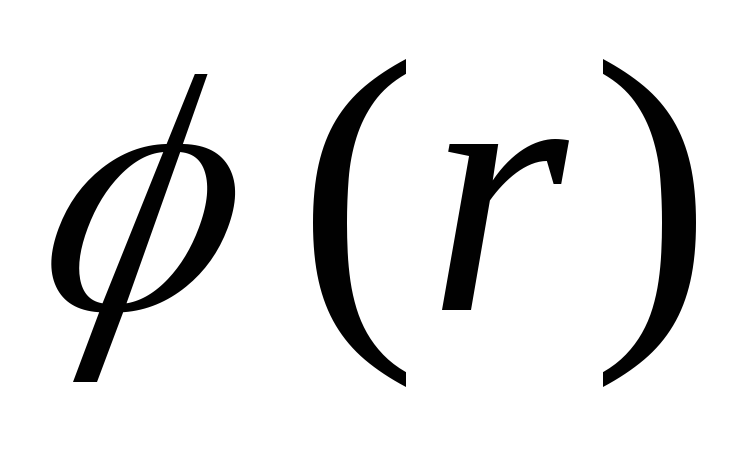 แสดงในรูปที่ ____
แสดงในรูปที่ ____
มาวิเคราะห์กราฟผลลัพธ์กัน
ตามเงื่อนไขของปัญหาสำหรับค่าที่กำหนด 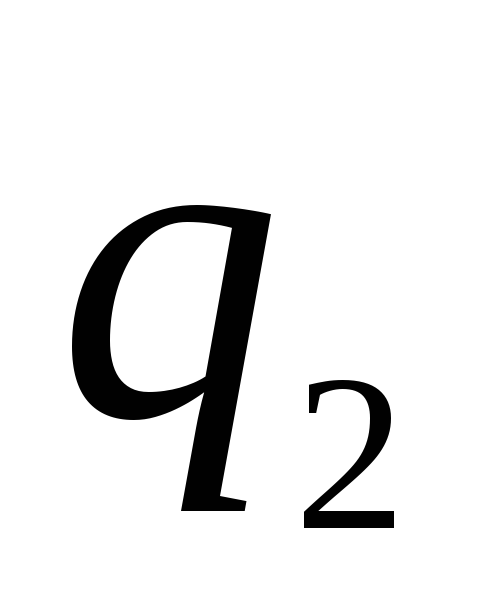 ศักยภาพบนพื้นผิวของทรงกลมชั้นใน
ศักยภาพบนพื้นผิวของทรงกลมชั้นใน 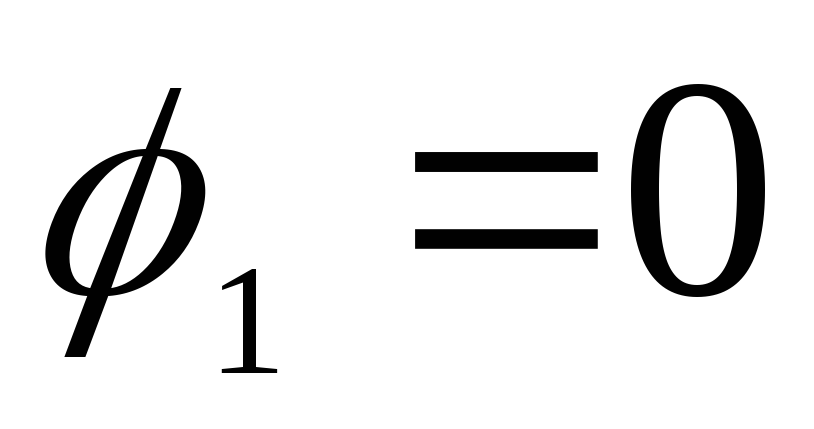 . ที่
. ที่ 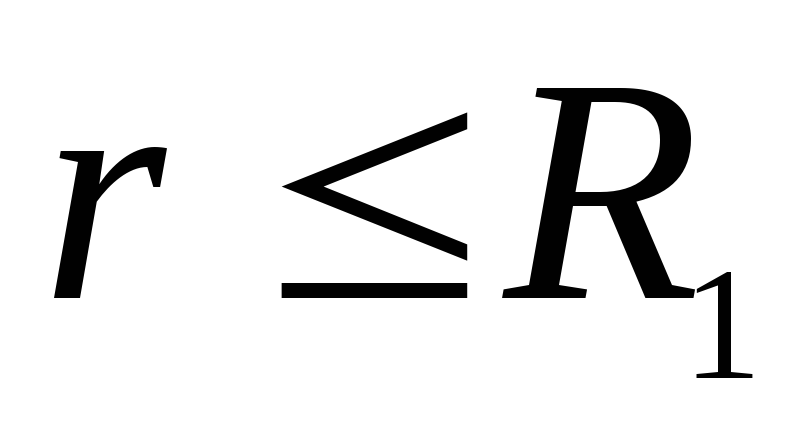 ศักย์จะคงที่และเท่ากับศักย์บนพื้นผิว ดังนั้น กราฟในพื้นที่จาก
ศักย์จะคงที่และเท่ากับศักย์บนพื้นผิว ดังนั้น กราฟในพื้นที่จาก 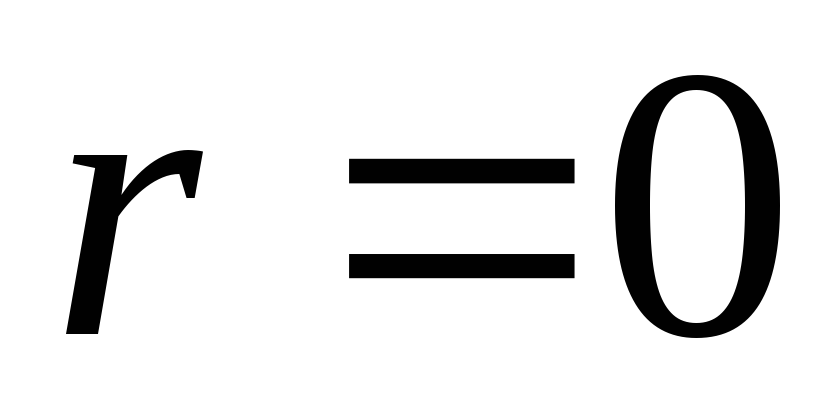 ก่อน
ก่อน 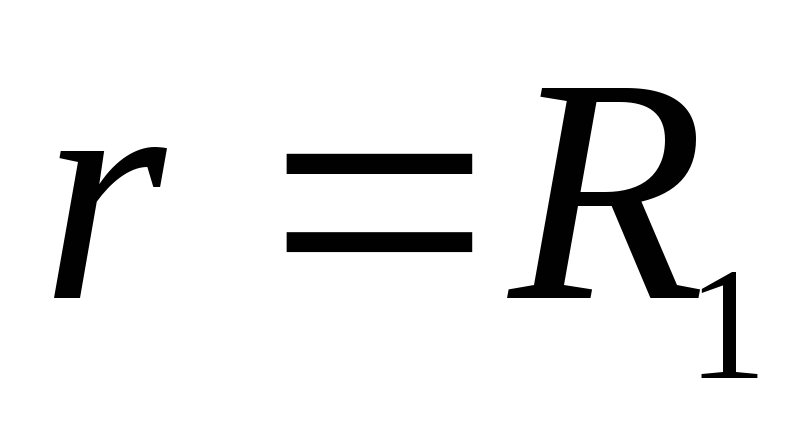 เป็นเส้นตรงประจวบกับแกน x ที่
เป็นเส้นตรงประจวบกับแกน x ที่ 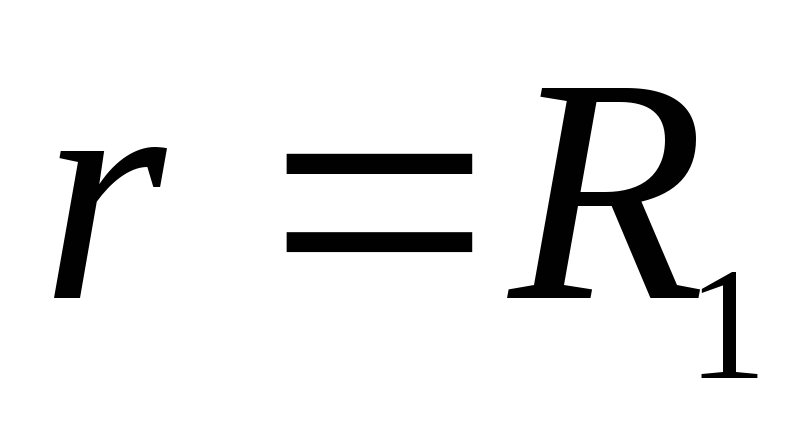 เวกเตอร์
เวกเตอร์  ทนทุกข์ทรมานจากการหยุดพัก เพราะ
ทนทุกข์ทรมานจากการหยุดพัก เพราะ 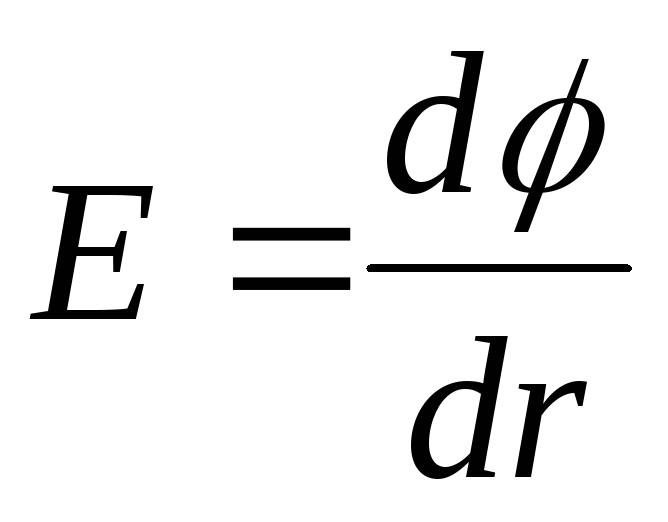 จากนั้นบนกราฟจุด
จากนั้นบนกราฟจุด 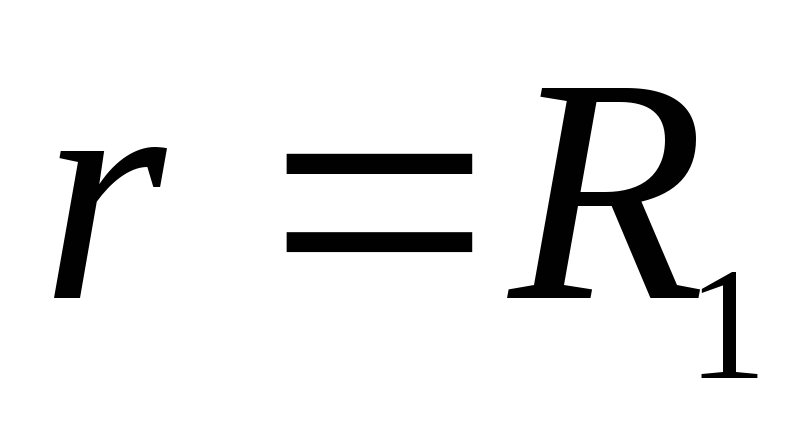 (เหมือนกับ dot
(เหมือนกับ dot 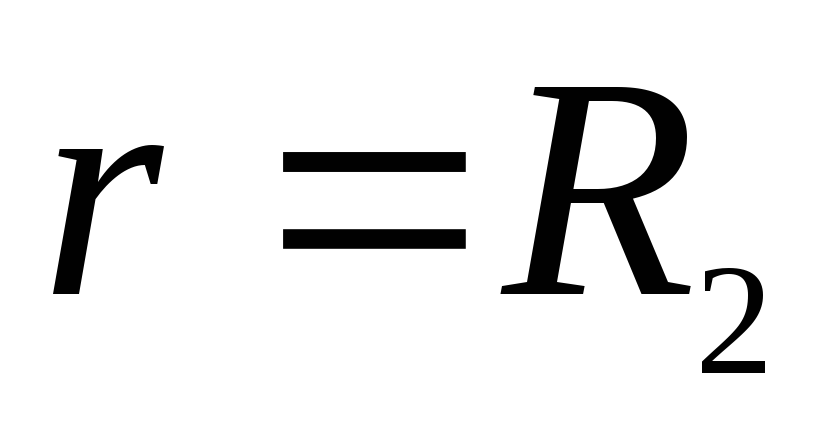 ) แทนจุดเอกพจน์ ตำแหน่งบน
) แทนจุดเอกพจน์ ตำแหน่งบน 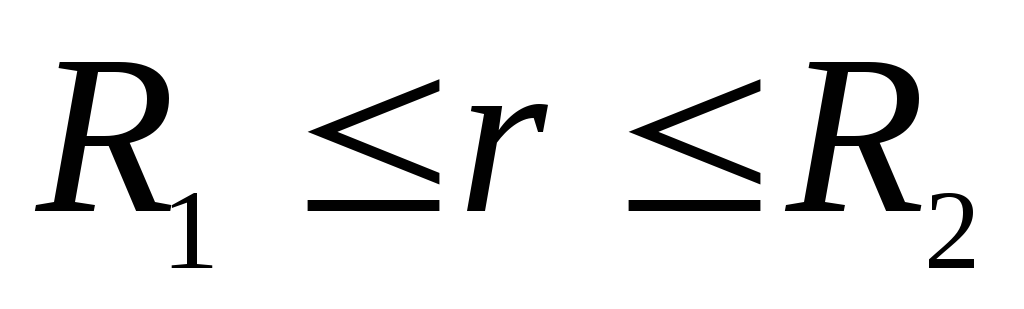 เวกเตอร์
เวกเตอร์  กำกับตามรัศมีเวกเตอร์
กำกับตามรัศมีเวกเตอร์ 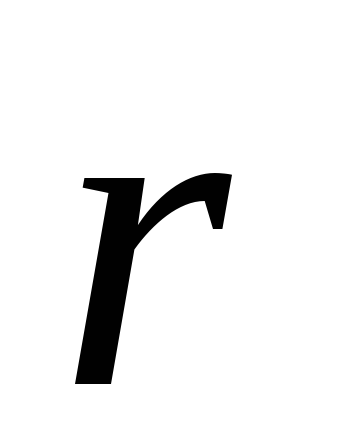 . ดังนั้น เมื่อเราเคลื่อนตัวออกจากพื้นผิวของทรงกลมชั้นใน ศักย์จะลดลงเป็นค่าหนึ่ง
. ดังนั้น เมื่อเราเคลื่อนตัวออกจากพื้นผิวของทรงกลมชั้นใน ศักย์จะลดลงเป็นค่าหนึ่ง 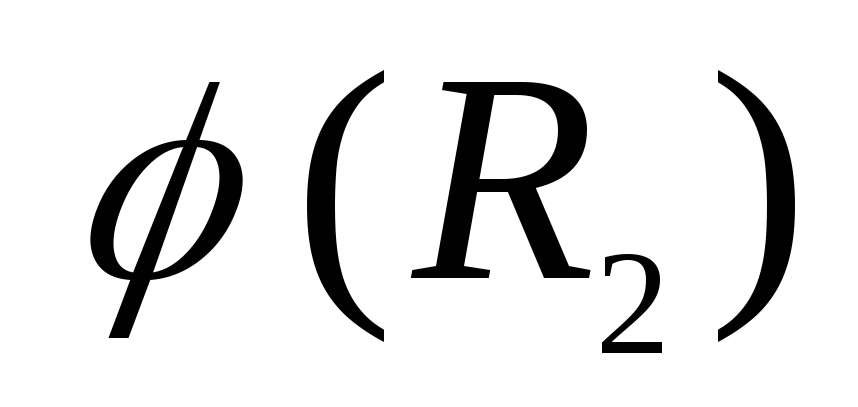 . ตำแหน่งบน
. ตำแหน่งบน 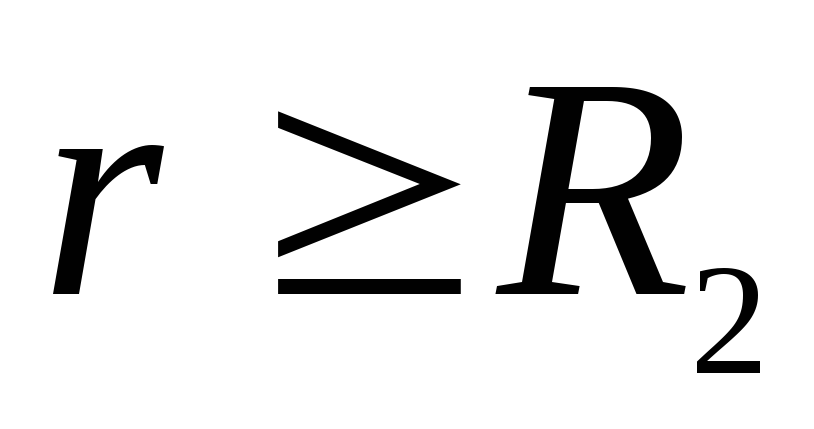 เวกเตอร์
เวกเตอร์  มุ่งสู่รัศมีเวกเตอร์
มุ่งสู่รัศมีเวกเตอร์ 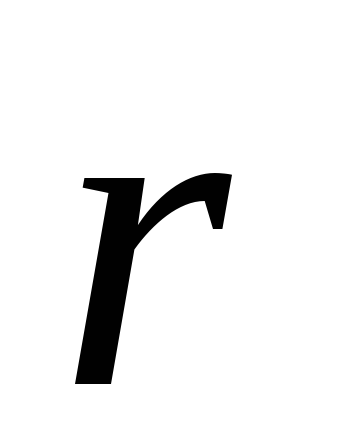 ดังนั้น เมื่อระยะห่างจากพื้นผิวของทรงกลมชั้นนอกเพิ่มขึ้น ศักยภาพจะเพิ่มขึ้น และที่
ดังนั้น เมื่อระยะห่างจากพื้นผิวของทรงกลมชั้นนอกเพิ่มขึ้น ศักยภาพจะเพิ่มขึ้น และที่ 
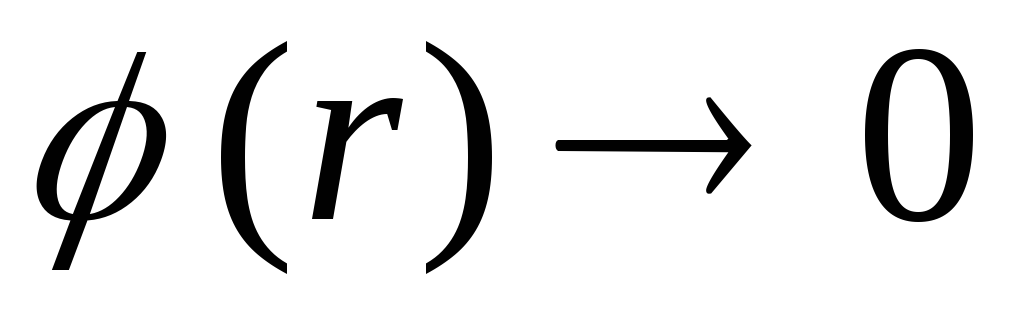 . แม้ว่า ณ จุดนั้น
. แม้ว่า ณ จุดนั้น 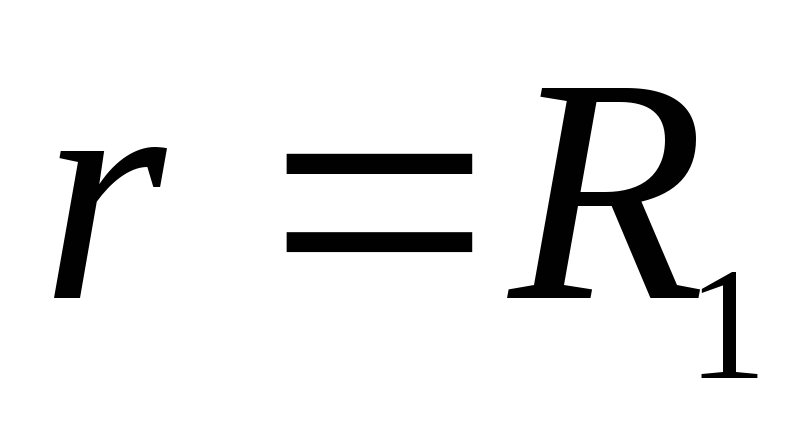 และ
และ 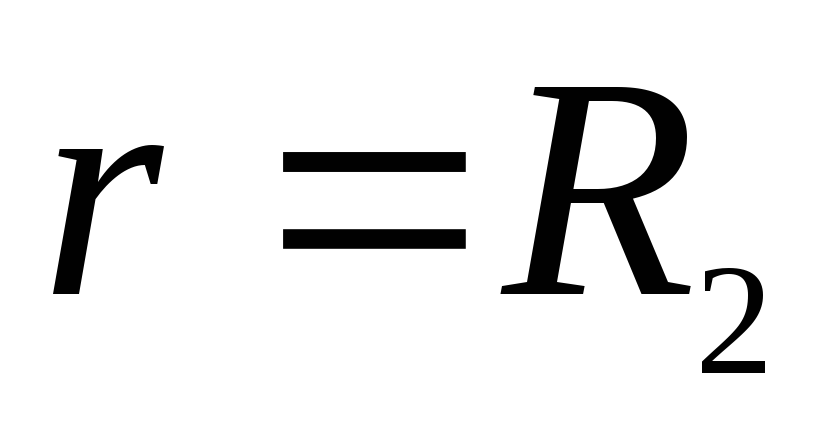 เวกเตอร์
เวกเตอร์  แบ่งการทำงาน
แบ่งการทำงาน 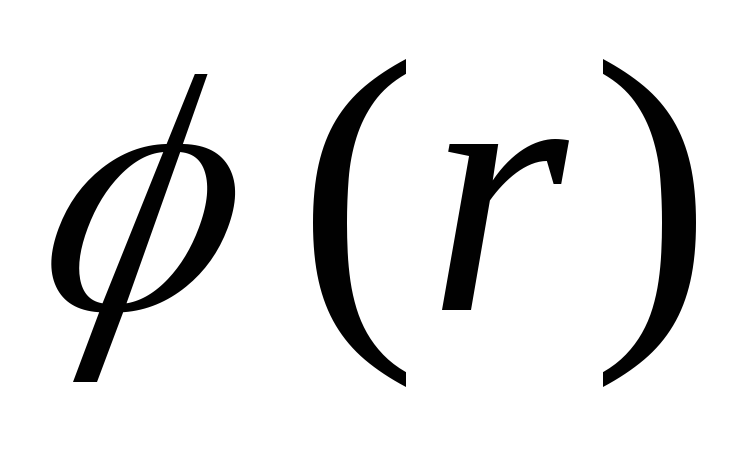 เป็นแบบต่อเนื่อง
เป็นแบบต่อเนื่อง
ในบรรดาปัญหาของโรงเรียนในวิชาฟิสิกส์ ผู้ที่เกี่ยวข้องกับทรงกลมที่มีศูนย์กลางเป็นศูนย์กลางนั้นแยกออกจากกัน ทรงกลมเหล่านี้สามารถชาร์จ, ต่อสายดิน, พวกเขาสามารถอยู่ในสนามของประจุภายนอก ฯลฯ มีหลายแบบ ที่ หลักสูตรโรงเรียนฟิสิกส์ ปัญหาเหล่านี้เป็นปัญหาที่ยากที่สุด สุดท้ายแต่ไม่ท้ายสุด แน่นอนว่าความเข้าใจผิดของเนื้อหานี้เกิดจากการที่ครูไม่สามารถอธิบายได้อย่างมีประสิทธิภาพและในลักษณะที่เข้าถึงได้ ลองหาว่าทรงกลมนำไฟฟ้าเหล่านี้คืออะไรและกินกับอะไร
ศักยภาพของทรงกลมชั้นใน φ 2 ถูกกำหนดโดยความสัมพันธ์ที่รู้จัก:
![]()
แล้วศักยภาพทั้งหมด φ บนพื้นผิวของทรงกลมชั้นในคือ:
ศักย์บนพื้นผิวของทรงกลมชั้นนอกยังประกอบด้วยศักย์อยู่สองอย่างคือ ทรงกลมชั้นใน φ’ 1 และทรงกลมชั้นนอกที่เหมาะสม φ’ 2 .
ศักยภาพของทรงกลมชั้นใน φ’ ห่างกัน1ที Rจากศูนย์กลางถูกกำหนดโดยความสัมพันธ์ที่รู้จัก:
![]()
สูตรที่กำหนดศักยภาพของทรงกลมชั้นนอก φ’ 2 บนพื้นผิวของมันยังเป็นที่รู้จักกันดี:
![]()
จากนั้นศักยภาพทั้งหมดบนพื้นผิวของทรงกลมชั้นนอกคือ:
![]()
วิธีการแก้.ก่อนเชื่อมต่อทรงกลมกับตัวนำ ประจุของอันแรกจะเท่ากับ:
หลังจากเชื่อมต่อแล้ว ประจุบางส่วนจากทรงกลมชั้นในจะไหลไปยังชั้นนอก กระแสหยุดในขณะที่ศักยภาพของลูกบอลเท่ากับศักยภาพของเปลือกนอก ดังนั้นจึงสะดวกกว่าที่จะไม่มองหาศักยภาพของลูกบอล แต่มองหาศักยภาพของเปลือกนอกเท่ากับมัน ตามผลลัพธ์ที่ได้รับในงานก่อนหน้านี้ ศักยภาพนี้ถูกกำหนดโดยนิพจน์:
![]()
ที่ไหน q 1 และ q 2 - ประจุของลูกบอลและเปลือกนอกหลังจากเชื่อมต่อกับตัวนำตามลำดับ ตามกฎการอนุรักษ์ประจุ q = q 1 + q 2. หลังจากแปลงอย่างง่าย เราได้รับ:
![]()
เริ่มต้นด้วยภาพเพื่อแก้ปัญหา:
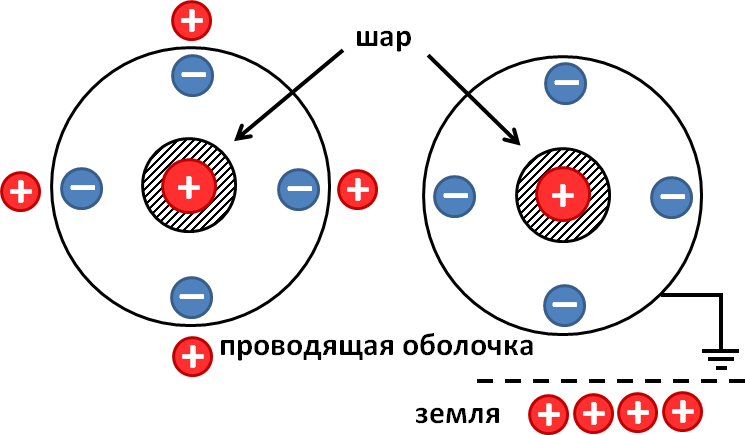
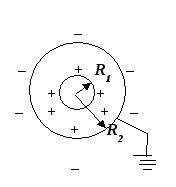
หลังจากการต่อสายดินของเปลือกนำไฟฟ้า ประจุบวกทั้งหมดจะเกิดขึ้นเนื่องจากปรากฏการณ์ของการเหนี่ยวนำไฟฟ้าสถิตที่ไหลลงสู่พื้น มีเพียงประจุลบเท่านั้นที่ยังคงอยู่เนื่องจากถูกดึงดูดไปยังประจุบวกของทรงกลมชั้นใน
วิธีการแก้.เมื่อทราบถึงศักยภาพของลูกบอลในช่วงเวลาเริ่มต้นและรัศมีของลูกบอล เราสามารถหาประจุบนลูกบอลได้:
เนื่องจากปรากฏการณ์การเหนี่ยวนำไฟฟ้าสถิตบนเปลือกนอก จึงต้องเกิดการแยกประจุ ประจุลบจะไหลไปยังพื้นผิวด้านในของเปลือก ประจุบวกไปยังประจุภายนอก (ดูรูป) ปรากฏการณ์เดียวกันนี้เกิดขึ้นในปัญหาก่อนหน้านี้ แต่เราไม่ได้คำนึงถึง ทำไม ในสภาวะของปัญหา พบว่าเปลือกบาง และประจุที่ "วิ่งหนี" ดังกล่าวไม่ได้นำไปสู่การเปลี่ยนแปลงที่สำคัญในการกำหนดค่าของสนามไฟฟ้าสถิต
ในงานนี้การบัญชี ปรากฏการณ์นี้สำคัญเพราะเปลือกมีสายดิน หลังจากต่อสายดินแล้ว ประจุบวกจากเปลือกจะระบายลงสู่พื้น แต่จะเหลือเพียงประจุลบเท่านั้น q 2 เพราะถูกดึงดูดด้วยประจุบวก q 1 วงใน. ศักยภาพของเปลือกที่ลงกราวด์จะเท่ากับศักยภาพของโลก นั่นคือศูนย์ ในเรื่องนี้และตามผลที่ได้รับในการแก้ปัญหาแรกเราได้รับความเท่าเทียมกัน:
การใช้นิพจน์เพื่อคำนวณศักยภาพของทรงกลมชั้นในของระบบดังกล่าว ซึ่งได้จากปัญหาแรก ในที่สุดเราก็พบศักยภาพที่ต้องการของลูกบอล:
![]()
![]()
ประสบการณ์แสดงให้เห็นว่าแทบไม่มีใครเข้าใจวิธีแก้ปัญหาเหล่านี้ในทุกรายละเอียดในครั้งแรก โดยปกติแล้วจะใช้เวลานานและสม่ำเสมอในการอธิบายสิ่งเล็กๆ น้อยๆ เหล่านั้นให้นักเรียนฟัง โดยไม่เข้าใจว่าวิธีแก้ปัญหานั้นถูกลดทอนเป็นการเปลี่ยนแปลงที่ว่างเปล่าของนิพจน์ตามตัวอักษร เพื่อให้ได้คำตอบที่ให้ไว้ท้ายหนังสือเรียน ไม่ใช่เรื่องง่ายที่จะเข้าใจสาระสำคัญทางกายภาพของงานเหล่านี้และเรียนรู้วิธีใช้ความรู้ที่ได้รับในอนาคต อย่างไรก็ตาม นี่คือคุณค่าวิธีการหลักของหัวข้อนี้ในหลักสูตรฟิสิกส์ของโรงเรียน ผู้ช่วยที่ดีที่สุดในการศึกษาจะต้องเป็นติวเตอร์มืออาชีพ ที่ปรึกษาที่มีความสามารถ ซึ่งสามารถให้คำอธิบายที่เข้าใจได้สำหรับคุณและตอบทุกคำถามของคุณ อย่างไรก็ตาม หากมี คุณสามารถถามพวกเขาด้านล่างในความคิดเห็น
Sergey Valerievich