Графік функції y=f(x)називається опуклимна інтервалі (a; b), якщо він розташований нижче за будь-яку свою дотичну на цьому інтервалі.
Графік функції y=f(x)називається увігнутимна інтервалі (a; b)якщо він розташований вище будь-якої своєї дотичної на цьому інтервалі.
На малюнку показана крива, опукла на (a; b)і увігнута на (b; c).
приклади.
Розглянемо достатню ознаку, що дозволяє встановити, чи графік функції у цьому інтервалі опуклим чи увігнутим.
Теорема. Нехай y=f(x)диференційована на (a; b). Якщо у всіх точках інтервалу (a; b)друга похідна функції y = f(x)негативна, тобто. f ""(x) < 0, то график функции на этом интервале выпуклый, если же f""(x) > 0 – увігнутий.
Доведення. Припустимо для певності, що f""(x) < 0 и докажем, что график функции будет выпуклым.
Візьмемо на графіку функції y = f(x)довільну точку M 0з абсцисою x 0 Î ( a; b) і проведемо через точку M 0дотичну. Її рівняння. Ми повинні показати, що графік функції на (a; b)лежить нижче від цієї дотичної, тобто. при тому самому значенні xордината кривої y = f(x)буде менше ординату дотичної.
Отже, рівняння кривої має вигляд y = f(x). Позначимо ординату щодо, відповідну абсцисі x. Тоді. Отже, різниця ординат кривої і дотичної при тому самому значенні xбуде.
Різниця f(x) – f(x 0)перетворимо за теоремою Лагранжа, де cміж xі x 0.
Таким чином,
До виразу, що стоїть у квадратних дужках, знову застосуємо теорему Лагранжа: , де з 1між з 0і x 0. За умовою теореми f ""(x) < 0. Определим знак произведения второго и третьего сомножителей.
Таким чином, будь-яка точка кривої лежить нижче за дотичну до кривої при всіх значеннях xі x 0 Î ( a; b), а це означає, що крива випукла. Друга частина теореми доводиться аналогічно.
Приклади.
Точка графіка безперервної функції, що відокремлює його опуклу частину від увігнутої, називається точкою перегину.
Вочевидь, що у точці перегину дотична, якщо вона існує, перетинає криву, т.к. з одного боку від цієї точки крива лежить під дотичною, з другого боку – з неї.
Визначимо достатні умови того, що дана точкакривою є точкою перегину.
Теорема. Нехай крива визначається рівнянням y = f(x). Якщо f ""(x 0) = 0 або f ""(x 0) немає і під час переходу через значення x = x 0похідна f ""(x) змінює знак, то точка графіка функції з абсцисою x = x 0є точка перегину.
Доведення. Нехай f ""(x) < 0 при x < x 0і f ""(x) > 0 при x > x 0. Тоді при x < x 0крива випукла, а при x > x 0- Увігнута. Отже, точка A, що лежить на кривій, з абсцисою x 0є точка перегину. Аналогічно можна розглядати другий випадок, коли f ""(x) > 0 при x < x 0і f ""(x) < 0 при x > x 0.
Таким чином, точки перегину слід шукати тільки серед таких точок, де друга похідна перетворюється на нуль або не існує.
приклади.Знайти точки перегину та визначити інтервали опуклості та увігнутості кривих.
АСИМПТОТИ ГРАФІКА ФУНКЦІЇ
Під час дослідження функції важливо встановити форму її графіка при необмеженому видаленні точки графіка від початку координат.
Особливий інтерес представляє випадок, коли графік функції при видаленні його змінної точки в безкінечність необмежено наближається до деякої прямої.
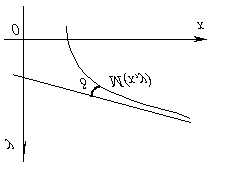
Пряма називається асимптотоюграфіка функції y = f(x), якщо відстань від змінної точки Mграфіка до цієї прямої при видаленні точки Mу нескінченність прагне нулю, тобто. точка графіка функції при своєму прагненні до нескінченності повинна необмежено наближатися до асимптота.
Крива може наближатися до своєї асимптоти, залишаючись з одного боку від неї або з різних боків, безліч разів перетинаючи асимптоту і переходячи з одного її боку на іншу.
Якщо позначимо через d відстань від точки Mкривою до асимптоти, то ясно, що d прагне нуля при видаленні точки Mу нескінченність.
Будемо надалі розрізняти асимптоти вертикальні та похилі.
ВЕРТИКАЛЬНІ АСИМПТОТИ
Нехай при x→ x 0з будь-якої сторони функція y = f(x)необмежено збільшується за абсолютною величиною, тобто. або або 
. Тоді з визначення асимптоти випливає, що пряма x = x 0є асимптотою. Очевидно і зворотне, якщо пряма x = x 0є асимптотою, т.ч. .
Таким чином, вертикальною асимптотою графіка функції y = f(x)називається пряма, якщо f(x)→ ∞ хоча б за однієї з умов x→ x 0- 0 або x → x 0 + 0, x = x 0
Отже, для відшукання вертикальних асимптот графіка функції y = f(x)потрібно знайти ті значення x = x 0, при яких функція перетворюється на нескінченність (терпить нескінченний розрив). Тоді вертикальна асимптота має рівняння x = x 0.
приклади.
НАКЛОННІ АСИМПТОТИ
Оскільки асимптота – це пряма, якщо крива y = f(x)має похилу асимптоту, то її рівняння буде y = kx + b. Наше завдання знайти коефіцієнти kі b.
Теорема. Пряма y = kx + bслужить похилою асимптотою при x→ +∞ для графіка функції y
= f(x)тоді і лише тоді, коли 
. Аналогічне твердження вірне і при x → –∞.
Доведення. Нехай MP- Довжина відрізка, що дорівнює відстані від точки Mдо асимптоти. За умовою . Позначимо через φ кут нахилу асимптоти до осі Ox. Тоді з ΔMNPвипливає, що . Оскільки φ постійний кут (φ ≠ π/2), то , але
За допомогою онлайн-калькулятора можна знайти точки перегину та проміжки опуклості графіка функціїз оформленням рішення у Word. Чи є функція двох змінних f(x1,x2) опуклою вирішується за допомогою матриці Гессе.
Правила введення функцій:
Напрямок опуклості графіка функції. Точки перегину
Визначення : Крива y=f(x) називається опуклою вниз у проміжку (a; b), якщо вона лежить вище за дотичну в будь-якій точці цього проміжку.Визначення: Крива y=f(x) називається опуклою вгору в проміжку (a; b), якщо вона лежить нижче за дотичну в будь-якій точці цього проміжку. 
Визначення: Проміжки, в яких графік функції звернений опуклістю вгору або вниз, називаються проміжками опуклості графіка функції.
Випуклість вниз або вгору кривої, що є графіком функції y=f(x) , характеризується знаком її другий похідної: якщо в деякому проміжку f'(x) > 0, то крива опукла вниз на цьому проміжку; якщо ж f’’(x)< 0, то кривая выпукла вверх на этом промежутке.
Визначення: Точка графіка функції y = f (x), що розділяє проміжки опуклості протилежних напрямів цього графіка, називається точкою перегину. 
Точками перегину можуть лише критичні точки II роду, тобто. точки, що належать області визначення функції y = f(x) , у яких друга похідна f''(x) звертається в нуль або зазнає розриву.
Правило знаходження точок перегину графіка функції y = f(x)
- Знайти другу похідну f''(x) .
- Визначити критичні точки II роду функції y=f(x) , тобто. точки, в якій f''(x) перетворюється на нуль або терпить розрив.
- Дослідити знак другої похідної f''(x) у проміжку, на які знайдені критичні точки ділять область визначення функції f(x) . Якщо у своїй критична точка x 0 поділяє проміжки опуклості протилежних напрямів, то x 0 є абсцисою точки перегину графіка функції.
- Обчислити значення функції у точках перегину.
приклад 1 . Знайти проміжки опуклості та точки перегину наступної кривої: f(x) = 6x2 –x3.
Рішення: Знаходимо f '(x) = 12x - 3x 2, f ''(x) = 12 - 6x.
Знайдемо критичні точки по другій похідній, розв'язавши рівняння 12-6x = 0. x=2. 
f(2) = 6*2 2 – 2 3 = 16
Відповідь: Функція опукла вгору при x∈(2; +∞); функція опукла вниз при x∈(-∞; 2); точка перегину (2; 16).
Приклад 2 . Чи має точки перегину функція: f(x)=x 3 -6x 2 +2x-1
Приклад 3 . Знайти проміжки, на яких графік функції опуклий і вигнутий: f(x)=x 3 -6x 2 +12x+4
диференційована на інтервалі (а, в). Тоді існує дотична до графіка функції у будь-якій точці 
цього графіка ( 
), причому дотична не паралельна осі OY , так як її кутовий коефіцієнт, що дорівнює 
, Кінцевий.
розподіл
на (а, в) має випускати, спрямовану вниз (вгору), якщо він розташований не нижче (не вище) будь-якої щодо графіку функції на (а, в). 
(
) у всіх точках цього інтервалу, то крива, що є графіком функції опукла (увігнута) на цьому інтервалі.
називається точкою перегину графіка функції, якщо в точці 
графік має дотичну, і існує така околиця точки 
, в межах якої графік функції ліворуч і праворуч точки має різні напрями опуклості.
Вочевидь, що у точці перегину дотична перетинає графік функції, оскільки з одного боку від цієї точки графік лежить над дотичною, з другого – під нею, т. е. на околиці точки перегину графік функції геометрично перетворюється з одного боку дотичної на іншу "перегинається" через неї. Звідси і походить назва «точки перегину».
безперервну другу похідну. Тоді 
.
не має перегину в точці (0, 0), хоча 
при 
. Тому рівність нулю другої похідної є лише необхідною умовою перегину. 
має 
має другу похідну в околиці точки, за винятком самої точки, і існує дотична до графіка функції в точці 
. Тоді, якщо в межах зазначеної околиці має різні знаки зліва і праворуч від точки, то графік функції має перегин у точці . 
на опуклість, увігнутість, точки перегину. 
, 
=
не існує при 
)
)
або поблизу точок розриву 2-го роду, часто виявляється, що графік функції скільки завгодно близько наближається до тієї чи іншої прямої. Такі прямі називають.
розподіл 1.
називається асимптотою кривої L, якщо відстань від точки кривої до цієї прямої прагне нуля при видаленні точки по кривій до нескінченності. Існує три види асимптоту: вертикальні, горизонтальні, похилі. 
називається вертикальною асимптотою графіка функції, якщо хоча б одна з односторонніх меж дорівнює 
, тобто 
має вертикальну асимптоту 
, т. до. 
, а 
.
якщо 
.
.
(
) називається похилою асимптотою графіка функції при 
якщо 
; 
.
; х = 0 - вертикальна асимптота
.
- похила асимптота. 
та побудувати її графік. 
функція ні парна ні непарна-
-
+
+
y
-4
т р.
0
Висновок.
Важливою особливістю розглянутого способу є те, що в його основі лежить насамперед виявлення та вивчення характерних рис у поведінці кривої. Місця, де функція змінюється плавно, не вивчаються особливо докладно, та й немає потреби у такому вивченні. Натомість ті місця, де функція має якісь особливості у поведінці, підлягають повному дослідженню та максимально точному графічному зображенню. Цими особливостями є точки максимуму, мінімуму, точки розриву функції та ін.
Визначення напрямку увігнутості та перегинів, а також зазначений спосіб знаходження асимптоту дають можливість провести дослідження функцій ще більш детально та отримати більш точне уявлення про їх графіки.
Поняття опуклості функції
Розглянемо функцію \(y = f\left(x \right),\) яка передбачається безперервною на відрізку \(\left[(a,b) \right].\) Функція \(y = f\left(x \right) )\) називається опуклою вниз (або просто опуклою), якщо для будь-яких точок \((x_1)\) і \((x_2)\) з \(\left[ (a,b) \right]\) виконується нерівність \ Якщо дана нерівність є суворою за будь-яких \(( x_1),(x_2) \in \left[ (a,b) \right],\) таких, що \((x_1) \ne (x_2),\) то функцію \(f\left(x \right) \) називають суворо опуклою вниз
Аналогічно визначається опукла догори функція. Функція \(f\left(x \right)\) називається опуклою вгору (або увігнутою), якщо для будь-яких точок \((x_1)\) і \((x_2)\) відрізка \(\left[(a,b) \right]\) справедлива нерівність \ Якщо ця нерівність є суворою за будь-яких \(( x_1),(x_2) \in \left[ (a,b) \right],\) таких, що \((x_1) \ne (x_2),\) то функцію \(f\left(x \right) \) називають суворо опуклою вгору на відрізку \(\left[(a,b)\right].\)
Геометрична інтерпретація опуклості функції
Введені визначення опуклої функції мають просту геометричну інтерпретацію.
Для функції, опуклою вниз (малюнок \(1\)), середина \(B\) будь-якої хорди \((A_1)(A_2)\) лежить вище
Аналогічно, для функції, опуклою вгору (малюнок \(2\)), середина \(B\) будь-якої хорди \((A_1)(A_2)\) лежить нижчевідповідної точки \((A_0)\) графіка функції або збігається з цією точкою.
Випуклі функції мають ще одну наочну властивість, яка пов'язана з розташуванням дотичної до графіка функції. Функція \(f\left(x \right)\) є опуклою вниз на відрізку \(\left[ (a,b) \right]\) тоді і тільки тоді, коли її графік лежить не нижче дотичної проведеної до нього в будь-якій точці \((x_0)\) відрізка \(\left[ (a ,b) \right]\) (малюнок \(3\)).
Відповідно, функція \(f\left(x \right)\) є опуклою вгору на відрізку \(\left[ (a,b) \right]\) тоді і тільки тоді, коли її графік лежить не вище за дотичну проведену до нього в будь-якій точці \((x_0)\) відрізка \(\left[ (a ,b) \right]\) (малюнок \(4\)). Дані властивості є теорему і можуть бути доведені з використанням визначення опуклості функції.
Достатні умови опуклості
Нехай для функції \(f\left(x \right)\) перша похідна \(f"\left(x \right)\) існує на відрізку \(\left[(a,b) \right],\) а друга похідна \(f""\left(x \right)\) − на інтервалі \(\left((a,b) \right).\) Тоді справедливі такі достатні ознаки опуклості:
Якщо \(f""\left(x \right) \ge 0\) при всіх \(x \in \left((a,b) \right),\) то функція \(f\left(x \right) )\) випукла вниз на відрізку \(\left[(a,b) \right];\)
Якщо \(f""\left(x \right) \le 0\) при всіх \(x \in \left((a,b) \right),\) то функція \(f\left(x \right) )\) випукла вгору на відрізку \(\left[(a,b)\right].\)
Доведемо наведену теорему для випадку опуклої функції вниз. Нехай функція \(f\left(x \right)\) має невід'ємну другу похідну на інтервалі \(\left((a,b) \right):\) \(f""\left(x \right) \ge 0.\) Позначимо через \((x_0)\) середину відрізка \(\left[((x_1),(x_2)) \right].\) Припустимо, що довжина цього відрізка дорівнює \(2h.\) Тоді координати \((x_1)\) і \((x_2)\) можна записати у вигляді: \[(x_1) = (x_0) - h,\;\;(x_2) = (x_0) + h.\] Розкладемо функцію \ (f \ left (x \ right) \) в точці \ ((x_0) \) в ряд Тейлора з залишковим членом у формі Лагранжа. Отримуємо наступні вирази: \[(f\left(((x_1)) \right) = f\left(((x_0) - h) \right) ) = (f\left(((x_0)) \right) - f"\left(((x_0)) \right)h + \frac((f""\left(((\xi _1)) \right)(h^2)))((2},}
\]
\[
{f\left({{x_2}} \right) = f\left({{x_0} + h} \right) }
= {f\left({{x_0}} \right) + f"\left({{x_0}} \right)h + \frac{{f""\left({{\xi _2}} \right){h^2}}}{{2!}},}
\]
где \({x_0} - h !}
Складемо обидві рівності: \[ (f\left(((x_1)) \right) + f\left(((x_2)) \right) ) = (2f\left(((x_0)) \right) + \frac (((h^2)))(2)\left[ (f""\left(((\xi _1)) \right) + f""\left(((\xi _2)) \right)) \right].) \] Оскільки \((\xi _1),(\xi _2) \in \left((a,b) \right),\) то другі похідні у правій частині невід'ємні. Отже, \ або \ тобто, відповідно до визначення, функція \(f\left(x \right)\) випукла вниз
.
Зазначимо, що необхідна умова опуклості функції (тобто. пряма теорема, у якій, наприклад, з умови опуклості вниз випливає, що (f"" \ left (x \ right) \ ge 0 \)) виконується лише для суворого нерівності. У разі суворої опуклості необхідна умова, власне кажучи, не дотримується. Наприклад, функція \(f\left(x \right) = (x^4)\) є строго опуклою вниз. Однак у точці (x = 0) її друга похідна дорівнює нулю, тобто. Сувора нерівність \(f""\left(x \right) \gt 0\) у цьому випадку не виконується.
Властивості опуклих функцій
Перерахуємо деякі властивості опуклих функцій, припускаючи, що всі функції визначені та безперервні на відрізку \(\left[(a,b)\right].\)
Якщо функції (f) і (g) опуклі вниз (вгору), то будь-яка їх лінійна комбінація \(af + bg,\) де \(a\), \(b\) - позитивні дійсні числа, також випукла вниз (вгору).
Якщо функція \(u = g\left(x \right)\) опукла вниз, а функція \(y = f\left(u \right)\) є опуклою вниз і незниженою, то складна функція \(y = f\left((g\left(x \right)) \right)\) буде також опуклою вниз.
Якщо функція \(u = g\left(x \right)\) опукла вгору, а функція \(y = f\left(u \right)\) є опуклою вниз і незростаючою, то складна функція \(y = f\left((g\left(x \right)) \right)\) буде опуклою вниз.
Локальний максимум опуклою вгору функції, заданої на відрізку \(\left[ (a,b) \right],\) є одночасно її найбільшим значенням на цьому відрізку.
Локальний мінімум опуклою вниз функції, заданої на відрізку \(\left[ (a,b) \right],\) є одночасно її найменшим значенням на цьому відрізку.
Коли ми креслимо графік функції, важливо визначити інтервали опуклості та точки перегину. Вони, поряд з проміжками спадання та зростання, потрібні нам для чіткого представлення функції у графічному вигляді.
Розуміння цієї теми вимагає знання того, що таке похідна функції та як її обчислити до певного порядку, а також уміння вирішувати різні видинерівностей.
На початку статті визначаються основні поняття. Потім ми покажемо, який зв'язок існує між напрямом опуклості та значенням другої похідної певному інтервалі. Далі ми зазначимо умови, у яких можна визначити точки перегину графіка. Усі міркування будуть проілюстровані прикладами розв'язання завдань.
Визначення 1У напрямку вниз на деякому інтервалі в тому випадку, коли її графік розташовується не нижче, ніж до нього до нього в будь-якій точці цього інтервалу.
Визначення 2
Диференційована функція є опуклоюу напрямку вгору на деякому інтервалі в тому випадку, якщо графік цієї функції розташовується не вище, ніж до нього до будь-якої точки цього інтервалу.
Опуклу вниз функцію можна назвати увігнутою. Обидва визначення наочно показані на графіку нижче:
Визначення 3
Точка перегину функції– це точка M (x 0 ; f (x 0)) , в якій існує дотична до графіка функції, за умови існування похідної на околиці точки x 0 , де з лівого та правого боку графік функції приймає різні напрями опуклості.
Простіше кажучи, точка перегину - це місце на графіку, в якому є дотична, і напрям опуклості графіка при проходженні через це місце буде змінювати напрям опуклості. Якщо ви не пам'ятаєте, за яких умов можливе існування вертикальної та невертикальної дотичної, радимо повторити розділ про дотичну графіку функції у точці.
Нижче наведено графік функції, що має кілька точок перегину, які виділені червоним. Уточнимо, що наявність точок перегину не є обов'язковою. На графіку однієї функції їх може бути одна, дві, кілька, нескінченно багато чи жодної.
У цьому пункті ми розповімо про теорему, за допомогою якої можна визначити проміжки опуклості на графіку конкретної функції.
Визначення 4
Графік функції матиме опуклість у напрямку вниз або вгору в тому випадку, якщо відповідна йому функція y = f (x) матиме другу кінцеву похідну на вказаному інтервалі x за умови, що нерівність f "" (x) ≥ 0 ∀ x ∈ X (f "" (x) ≤ 0 ∀ x ∈ X) буде вірним.
Використовуючи цю теорему, можна знайти проміжки увігнутості та опуклості на будь-якому графіку функції. Для цього потрібно просто вирішити нерівності f "" (x) ≥ 0 і f "" (x) ≤ 0 на ділянці визначення відповідної функції.
Уточнимо, що ті точки, в яких друга похідна не існує, але функція y = f(x) визначена, включатимуться в інтервали опуклості та увігнутості.
Подивимося на прикладі конкретного завданняяк правильно застосовувати цю теорему.
Приклад 1
Умова:дана функція y = x 3 6 - x 2 + 3 x - 1. Визначте, на яких проміжках її графік матиме опуклості та увігнутості.
Рішення
Областью визначення цієї функції є безліч дійсних чисел. Почнемо з обчислення другої похідної.
y " = x 3 6 - x 2 + 3 x - 1 " = x 2 2 - 2 x + 3 ⇒ y " " = x 2 2 - 2 x + 3 = x - 2
Ми бачимо, що область визначення другої похідної збіглася з областю самої функції. Отже, для виявлення інтервалів опуклостей нам треба вирішити нерівності f "" (x) ≥ 0 і f "" (x) ≤ 0 .
y "" ≥ 0 ⇔ x - 2 ≥ 0 ⇔ x ≥ 2 y "" ≤ 0 ⇔ x - 2 ≤ 0 ⇔ x ≤ 2
Ми отримали, що графік заданої функції матиме увігнутість на відрізку [2; + ∞) та опуклість на відрізку (- ∞ ; 2 ] .
Для наочності зобразимо графік функції та відзначимо на ньому опуклу частину синім, а увігнуту – червоним кольором.
Відповідь:графік заданої функції матиме увігнутість на відрізку [2; + ∞) та опуклість на відрізку (- ∞ ; 2 ] .
А що ж робити, якщо область визначення другої похідної не збігається з областю визначення функції? Тут нам знадобиться зауваження, зроблене вище: ті точки, де кінцева друга похідна не існує, ми теж включатимемо у відрізки увігнутості та опуклості.
Приклад 2
Умова:дана функція y = 8 x x - 1. Визначте, у яких проміжках її графік матиме увігнутість, а яких – опуклість.
Рішення
Для початку з'ясуємо область визначення функції.
x ≥ 0 x - 1 ≠ 0 ⇔ x ≥ 0 x ≠ 1 ⇔ x ∈ [0; 1) ∪ (1; + ∞)
Тепер обчислюємо другу похідну:
y " = 8 x x - 1 " = 8 · 1 2 x · (x - 1) - x · 1 (x - 1) 2 = - 4 · x + 1 x · (x - 1) 2 y "" = - 4 · x + 1 x · (x - 1) 2 " = - 4 · 1 · x · x - 1 2 - (x + 1) · x · x - 1 2 " x · (x - 1) 4 = = - 4 · 1 · x · x - 1 2 - x + 1 · 1 2 x · (x - 1) 2 + x · 2 (x - 1) x · x - 1 4 = = 2 · 3 x 2 + 6 x - 1 x 3 2 · (x - 1) 3
Область визначення другої похідної – це множина x ∈ (0 ; 1) ∪ (1 ; + ∞) . Ми бачимо, що x , що дорівнює нулю, буде належати області визначення вихідної функції, але не області визначення другої похідної. Цю точку потрібно обов'язково включити у відрізок увігнутості чи опуклості.
Після цього треба вирішити нерівності f " " (x) ≥ 0 і f " " (x) ≤ 0 області визначення заданої функції. Використовуємо для цього метод інтервалів: при x = - 1 - 2 3 3 ≈ - 2 , 1547 або x = - 1 + 2 3 3 ≈ 0 , 1547 чисельник 2 · (3 x 2 + 6 x - 1) x 2 3 · x - 1 3 звертається до 0 , а знаменник дорівнює 0 при x , що дорівнює нулю або одиниці.
Нанесемо точки на графік, що вийшли, і визначимо знак виразу на всіх інтервалах, які увійдуть в область визначення вихідної функції. На графіці ця область позначена штрихуванням. Якщо значення позитивне, відзначаємо інтервал плюсом, якщо негативним, то мінусом.
Отже,
f "" (x) ≥ 0 x ∈ [ 0 ; 1) ∪ (1; + ∞) ⇔ x ∈ 0; - 1 + 2 3 3 ∪ (1; + ∞), а f "" (x) ≤ 0 x ∈ [0; 1) ∪ (1; + ∞) ⇔ x ∈ [- 1 + 2 3 3; 1)
Включаємо раніше зазначену точку x = 0 і отримуємо відповідь. Графік вихідної функції матиме опуклість у напрямку вниз при 0; - 1 + 2 3 3 ∪ (1 ; + ∞) , і вгору – при x ∈ [- 1 + 2 3 3 ; 1).
Зобразимо графік, відзначивши на ньому опуклу частину синім, а увігнуту червоним кольором. Вертикальна асимптотавідзначена чорним пунктиром.
Відповідь:Графік вихідної функції матиме опуклість у напрямку вниз при 0; - 1 + 2 3 3 ∪ (1 ; + ∞) , і вгору – при x ∈ [- 1 + 2 3 3 ; 1).
Умови перегину графіка функції
Почнемо з формулювання необхідної умови перегину графіка певної функції.
Визначення 5
Припустимо, що ми маємо функцію y = f (x) , графік якої має точку перегину. При x = x 0 він має безперервна друга похідна, отже, виконуватиметься рівність f " " (x 0) = 0 .
Враховуючи цю умову, нам слід пошукати точки перегину серед тих, у яких друга похідна звертатиметься до 0 . Ця умова не буде достатньою: не всі такі точки нам підійдуть.
Також зверніть увагу, що, згідно з загальним визначенням, нам потрібна буде пряма, вертикальна або невертикальна. Насправді це означає, що з знаходження точок перегину слід узяти ті, у яких друга похідна цієї функції звертається до 0 . Отже, щоб знайти абсциси точок перегину, нам потрібно взяти всі x 0 з області визначення функції, де lim x → x 0 - 0 f "(x) = ∞ і lim x → x 0 + 0 f" (x) = ∞ . Найчастіше це такі точки, у яких знаменник першої похідної звертається до 0 .
Перша достатня умова існування точки перегину графіка функції
Ми знайшли всі значення x 0 , які можна взяти як абсцис точок перегину. Після цього нам потрібно застосувати першу достатню умову перегину.
Визначення 6
Припустимо, що ми маємо функцію y = f (x) , яка є безперервною в точці M (x 0 ; f (x 0)) . При цьому вона має на цій точці дотичну, а сама функція має другу похідну на околиці цієї точки x 0 . У такому разі якщо з лівого та правого боку друга похідна набуває протилежних знаків, то дану точку можна вважати точкою перегину.
Ми бачимо, що ця умова не вимагає, що в цій точці неодмінно існувала друга похідна, достатньо її наявності на околиці точки x 0 .
Все сказане вище зручно подати у вигляді послідовності дій.
- Для початку потрібно знайти всі абсциси x 0 можливих точок перегину, де f "" (x 0) = 0 lim x → x 0 - 0 f "(x) = ∞ lim x → x 0 + 0 f " (x) = ∞.
- З'ясуємо, у яких точках похідна мінятиме знак. Ці значення є абсциси точок перегину, а точки M (x 0 ; f (x 0)) , відповідні їм, – це самі точки перегину.
Для наочності розберемо дві задачі.
Приклад 3
Умова:дана функція y = 1 10 · x 4 12 - x 3 6 - 3 x 2 + 2 x. Визначте, де графік цієї функції матиме точки перегину та опуклості.
Рішення
Зазначена функція визначена на всій кількості дійсних чисел. Вважаємо першу похідну:
y " = 1 10 · x 4 12 - x 3 6 - 3 x 2 + 2 x " = 1 10 · 4 x 3 12 - 3 x 2 6 - 6 x + 2 = = 1 10 · x 3 3 - x 2 2 - 6 x + 2
Тепер знайдемо область визначення першої похідної. Це також безліч усіх дійсних чисел. Отже, рівності lim x → x 0 - 0 f "(x) = ∞ і lim x → x 0 + 0 f "(x) = ∞ не можуть бути виконані за жодних значень x 0 .
Обчислюємо другу похідну:
y " " = = 1 10 · x 3 3 - x 2 2 - 6 x + 2 " = 1 10 · 3 x 2 3 - 2 x 2 - 6 = 1 10 · x 2 - x - 6
y "" = 0 ⇔ 1 10 · (x 2 - x - 6) = 0 ⇔ x 2 - x - 6 = 0 D = (- 1) 2 - 4 · 1 · (- 6) = 25 x 1 = 1 - 25 2 = - 2 x 2 = 1 + 25 2 = 3
Ми знайшли абсциси двох ймовірних точок перегину – 2 та 3 . Все, що нам залишилося зробити, – це перевірити, в якій точці похідна змінить свій знак. Зобразимо числову вісь і нанесемо на неї дані точки, після чого розставимо знаки другої похідної на проміжках, що виходять.
Дуги показують напрямок опуклості графіка в кожному інтервалі.
Друга похідна змінює знак на протилежний (з плюса на мінус) в точці з абсцисою 3 проходячи через неї зліва направо, і також робить це (з мінуса на плюс) в точці з абсцисою 3 . Отже, ми можемо дійти невтішного висновку, що x = - 2 і x = 3 – це абсциси точок перегину графіка функції. Їм відповідатимуть точки графіка - 2; - 4 3 і 3; - 15 8 .
Поглянемо знову на зображення числової осі і знаки, що вийшли на інтервалах, щоб зробити висновки про місця увігнутості і опуклості. Виходить, що опуклість буде розташована на відрізку - 2; 3 , а увігнутість на відрізках (- ∞ ; - 2 ) і [ 3 ; + ∞) .
Розв'язання задачі наочно зображено на графіку: синій колір – опуклості, червоний – увігнутість, чорний колір означає точки перегину.
Відповідь:опуклість буде розташована на відрізку - 2; 3 , а увігнутість на відрізках (- ∞ ; - 2 ) і [ 3 ; + ∞) .
Приклад 4
Умова:обчисліть абсциси всіх точок перегину графіка функції y = 1 8 · x 2 + 3 x + 2 · x - 3 3 5 .
Рішення
Область визначення заданої функції – безліч дійсних чисел. Обчислюємо похідну:
y " = 1 8 · (x 2 + 3 x + 2) · x - 3 3 5 " = = 1 8 · x 2 + 3 x + 2 " · (x - 3) 3 5 + (x 2 + 3 x + 2) · x - 3 3 5 " = = 1 8 · 2 x + 3 · (x - 3) 3 5 + (x 2 + 3 x + 2) · 3 5 · x - 3 - 2 5 = 13 x 2 - 6 x - 39 40 · (x - 3) 2 5
На відміну від функції, її перша похідна не буде визначена при значенні x , рівному 3 але:
lim x → 3 - 0 y "(x) = 13 · (3 - 0) 2 - 6 · (3 - 0) - 39 40 · 3 - 0 - 3 2 5 = + ∞ lim x → 3 + 0 y" (x) = 13 · (3 + 0) 2 - 6 · (3 + 0) - 39 40 · 3 + 0 - 3 2 5 = + ∞
Це означає, що через цю точку проходитиме вертикальна дотична до графіка. Отже, 3 може бути абсцисою точки перегину.
Обчислюємо другу похідну. Також знаходимо область її визначення та точки, в яких вона звертається до 0:
y "" = 13 x 2 - 6 x - 39 40 · x - 3 2 5 " = = 1 40 · 13 x 2 - 6 x - 39 " · (x - 3) 2 5 - 13 x 2 - 6 x - 39 · x - 3 2 5 "(x - 3) 4 5 = = 1 25 · 13 x 2 - 51 x + 21 (x - 3) 7 5 , x ∈ (- ∞ ; 3) ∪ (3 ; + ∞ ) y "" (x) = 0 ⇔ 13 x 2 - 51 x + 21 = 0 D = (- 51) 2 - 4 · 13 · 21 = 1509 x 1 = 51 + 1509 26 ≈ 3 , 4556 , x 2 = 51 - 1509 26 ≈ 0 , 4675
У нас вийшло ще дві можливі точки перегину. Нанесемо їх все на числову пряму і розмітимо інтервали, що виходять, знаками:
Зміна знака відбуватиметься при проходженні через кожну вказану точку, отже, всі вони є точками перегину.
Відповідь:Зобразимо графік функції, відзначивши увігнутості червоним, опуклості синім та точки перегину – чорним:
Знаючи першу достатню умову перегину, ми можемо визначити потрібні точки, у яких необов'язково наявність другої похідної. Виходячи з цього, перша умова можна вважати найбільш універсальною та придатною для вирішення різних типів завдань.
Зазначимо, що є ще дві умови перегину, проте їх можна застосовувати лише тоді, коли у зазначеній точці є кінцева похідна.
Якщо маємо f " " (x 0) = 0 і f " " (x 0) ≠ 0 , то x 0 буде абсцисою точки перегину графіка y = f (x) .
Приклад 5
Умова:задана функція y = 160 x 3 - 3 20 x 2 + 7 10 x - 2 5 . Визначте, чи графік функції матиме перегин у точці 3 ; 4 5 .
Рішення
Перше, що потрібно зробити, – це переконатися в тому, що ця точка взагалі належатиме графіку цієї функції.
y(3) = 1 60 · 3 3 - 3 20 · 3 2 - 2 5 = 27 60 - 27 20 + 21 10 - 2 5 = 9 - 27 + 42 - 8 20 = 4 5
Ця функція визначена для всіх аргументів, що є дійсними числами. Обчислимо першу та другу похідні:
y" = 1 60 x 3 - 3 20 x 2 + 7 10 x - 2 5" = 1 20 x 2 - 3 10 x + 7 10 y "" = 1 20 x 2 - 3 10 x + 7 10 " = 1 10 x - 3 10 = 1 10 (x - 3)
Ми отримали, що друга похідна буде звертатися до 0 , якщо x дорівнюватиме 0 . Отже, необхідна умова перегину цієї точки буде виконано. Тепер використовуємо другу умову: знайдемо третю похідну і з'ясуємо, чи звертатиметься вона в 0 при 3:
y " " " = 1 10 (x - 3) " = 1 10
Третя похідна не буде звертатися в нуль за жодного значення x. Тому можна зробити висновок, що дана точка буде точкою перегину графіка функції.
Відповідь:Покажемо рішення на ілюстрації:
Припустимо, що f "(x 0) = 0, f "" (x 0) = 0, ..., f (n) (x 0) = 0 і f (n + 1) (x 0) ≠ 0 . У такому разі при парному n ми отримаємо, що x 0 – це абсцис точки перегину графіка y = f(x).
Приклад 6
Умова:дана функція y = (x – 3) 5 + 1 . Обчисліть точки перегину її графіка.
Рішення
Ця функція є визначеною по всьому множині дійсних чисел. Обчислюємо похідну: y "= ((x - 3) 5 + 1)" = 5 · x - 3 4 . Оскільки вона теж буде визначена для всіх дійсних значень аргументу, то в будь-якій точці її графіка існуватиме невертикальна дотична.
Тепер обчислимо, при яких значеннях друга похідна буде звертатися до 0:
y "" = 5 · (x - 3) 4 " = 20 · x - 3 3 y "" = 0 ⇔ x - 3 = 0 ⇔ x = 3
Ми отримали, що за x = 3 графік функції може мати точку перегину. Використовуємо третю умову, щоб підтвердити це:
y " " " = 20 · (x - 3) 3 " = 60 · x - 3 2 , y " " " (3) = 60 · 3 - 3 2 = 0 y (4) = 60 · (x - 3) 2 "= 120 · (x - 3), y (4) (3) = 120 · (3 - 3) = 0 y (5) = 120 · (x - 3)" = 120, y (5) (3 ) = 120 ≠ 0
Маємо n = 4 за третьою достатньою умовою. Це парне число, отже, x = 3 буде абсцисою точки перегину і відповідає точка графіка функції (3 ; 1) .
Відповідь:Ось графік цієї функції із зазначеними опуклостями, увігнутостями та точкою перегину:
Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter