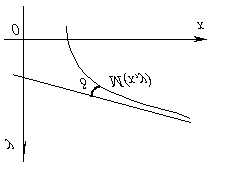
กราฟฟังก์ชัน y=เอฟ(x)เรียกว่า นูนในช่วงเวลา (ก;ข)ถ้าอยู่ต่ำกว่าแทนเจนต์ใดๆ ในช่วงเวลานี้
กราฟฟังก์ชัน y=เอฟ(x)เรียกว่า เว้าในช่วงเวลา (ก;ข)ถ้าอยู่เหนือแทนเจนต์ใดๆ ในช่วงเวลานี้
รูปแสดงเส้นโค้งนูนบน (ก;ข)และเว้าถึง (ข;ค).
ตัวอย่าง.
พิจารณาสัญญาณที่เพียงพอที่ช่วยให้คุณกำหนดได้ว่ากราฟของฟังก์ชันในช่วงเวลาที่กำหนดจะนูนหรือเว้า
ทฤษฎีบท. อนุญาต y=เอฟ(x)แยกความแตกต่างได้โดย (ก;ข). ถ้าทุกจุดของช่วงเวลา (ก;ข)อนุพันธ์อันดับสองของฟังก์ชัน y = เอฟ(x)เชิงลบ กล่าวคือ ฉ ""(x) < 0, то график функции на этом интервале выпуклый, если же ฉ""(x) > 0 คือเว้า
การพิสูจน์. สมมติความแน่วแน่ว่า ฉ""(x) < 0 и докажем, что график функции будет выпуклым.
ใช้กราฟฟังก์ชัน y = ฉ(x)จุดโดยพลการ M0กับ abscissa x0 Î ( เอ; ข) และลากผ่านจุด M0แทนเจนต์ สมการของเธอ เราต้องแสดงว่ากราฟของฟังก์ชันบน (ก;ข)อยู่ใต้แทนเจนต์นี้ กล่าวคือ มีค่าเท่ากัน xการปรับเส้นโค้ง y = ฉ(x)จะน้อยกว่าพิกัดของแทนเจนต์
ดังนั้นสมการของเส้นโค้งคือ y = ฉ(x). ให้เราแสดงแทนเจนต์ที่สอดคล้องกับ abscissa x. แล้ว . ดังนั้นความแตกต่างระหว่างพิกัดของเส้นโค้งและแทนเจนต์ที่ค่าเดียวกัน xจะ .
ความแตกต่าง ฉ(x) – ฉ(x0)แปลงตามทฤษฎีบทลากรองจ์ โดยที่ คระหว่าง xและ x0.
ทางนี้,
เราใช้ทฤษฎีบทลากรองจ์อีกครั้งกับนิพจน์ในวงเล็บเหลี่ยม: , โดยที่ ค 1ระหว่าง ค 0และ x0. ตามทฤษฎีบท ฉ ""(x) < 0. Определим знак произведения второго и третьего сомножителей.
ดังนั้น จุดใดๆ ของเส้นโค้งจะอยู่ใต้เส้นสัมผัสของเส้นโค้งสำหรับค่าทั้งหมด xและ x0 Î ( เอ; ข) ซึ่งหมายความว่าส่วนโค้งนูน ส่วนที่สองของทฤษฎีบทได้รับการพิสูจน์ในทำนองเดียวกัน
ตัวอย่าง.
จุดบนกราฟของฟังก์ชันต่อเนื่องที่แยกส่วนที่นูนออกจากส่วนที่เว้าเรียกว่า จุดสะท้อน.
แน่นอน ที่จุดเปลี่ยนเว้า แทนเจนต์ ถ้ามี จะตัดกับเส้นโค้ง เพราะ ด้านหนึ่งของจุดนี้ เส้นโค้งอยู่ใต้เส้นสัมผัส และอีกด้านหนึ่ง เหนือจุดนั้น
ให้เรากำหนดเงื่อนไขที่เพียงพอสำหรับข้อเท็จจริงที่ว่า คะแนนที่กำหนดเส้นโค้งเป็นจุดเปลี่ยน
ทฤษฎีบท. ให้เส้นโค้งถูกกำหนดโดยสมการ y = ฉ(x). ถ้า ฉ ""(x 0) = 0 หรือ ฉ ""(x 0) ไม่มีอยู่และเมื่อผ่านค่า x = x0อนุพันธ์ ฉ ""(x) เปลี่ยนเครื่องหมาย จากนั้นจุดกราฟของฟังก์ชันด้วย abscissa x = x0มีจุดเปลี่ยน
การพิสูจน์. อนุญาต ฉ ""(x) < 0 при x < x0และ ฉ ""(x) > 0 at x > x0. แล้วที่ x < x0เส้นโค้งนูนและ x > x0- เว้า ดังนั้นประเด็น อา, นอนบนโค้ง, มี abscissa x0มีจุดเปลี่ยน ในทำนองเดียวกัน เราสามารถพิจารณากรณีที่สองเมื่อ ฉ ""(x) > 0 at x < x0และ ฉ ""(x) < 0 при x > x0.
ดังนั้น ควรหาจุดเปลี่ยนเว้าเฉพาะในจุดที่อนุพันธ์อันดับสองหายไปหรือไม่มีอยู่จริง
ตัวอย่าง.หาจุดเปลี่ยนเว้าและกำหนดช่วงเวลานูนและความเว้าของเส้นโค้ง
สมการของกราฟของฟังก์ชัน
ในการตรวจสอบฟังก์ชัน สิ่งสำคัญคือต้องสร้างรูปร่างของกราฟด้วยการนำจุดกราฟออกจากจุดเริ่มต้นอย่างไม่จำกัด
สิ่งที่น่าสนใจเป็นพิเศษคือกรณีที่กราฟของฟังก์ชัน เมื่อจุดตัวแปรถูกลบออกจนเป็นอนันต์ จะเข้าใกล้เส้นตรงเส้นหนึ่งอย่างไม่มีกำหนด
เรียกตรงว่า เส้นกำกับกราฟฟังก์ชัน y = เอฟ(x)ถ้าระยะห่างจากจุดแปรผัน เอ็มกราฟเส้นนี้เมื่อจุดถูกลบออก เอ็มถึงอินฟินิตี้มีแนวโน้มที่จะเป็นศูนย์เช่น จุดของกราฟของฟังก์ชัน เนื่องจากมีแนวโน้มเป็นอนันต์ ต้องเข้าใกล้เส้นกำกับอย่างไม่มีกำหนด
เส้นโค้งสามารถเข้าใกล้เส้นกำกับของมัน โดยคงอยู่ด้านใดด้านหนึ่งหรือด้านต่างๆ กัน ตัดเส้นกำกับเป็นจำนวนอนันต์และเคลื่อนจากด้านหนึ่งไปอีกด้านหนึ่ง
หากเราแทนด้วย d ระยะทางจากจุดนั้น เอ็มโค้งไปยังเส้นกำกับเป็นที่ชัดเจนว่า d มีแนวโน้มที่จะเป็นศูนย์เมื่อจุดนั้นถูกลบออก เอ็มไม่มีที่สิ้นสุด.
เราจะแยกความแตกต่างระหว่างเส้นกำกับแนวตั้งและแนวเฉียงเพิ่มเติม
เส้นกำกับแนวตั้ง
ให้ที่ x→ x0ด้านใดด้านหนึ่งของฟังก์ชัน y = เอฟ(x)ค่าสัมบูรณ์เพิ่มขึ้นอย่างไม่มีกำหนด กล่าวคือ หรือหรือ 
. ต่อจากนิยามของเส้นกำกับว่าเส้น x = x0เป็นเส้นกำกับ การสนทนาก็ชัดเจนเช่นกันถ้าบรรทัด x = x0เป็นเส้นกำกับ ดังนั้น .
ดังนั้นเส้นกำกับแนวตั้งของกราฟของฟังก์ชัน y = ฉ(x)เรียกว่าเส้น if เอฟ(x)→ ∞ ภายใต้เงื่อนไขอย่างน้อยหนึ่งข้อ x→ x0– 0 หรือ x → x0 + 0, x = x0
ดังนั้น ในการหาเส้นกำกับแนวตั้งของกราฟของฟังก์ชัน y = เอฟ(x)ต้องหาค่าเหล่านั้น x = x0ที่ฟังก์ชันไปที่อนันต์ (ประสบกับความไม่ต่อเนื่องที่ไม่มีที่สิ้นสุด) จากนั้นเส้นกำกับแนวตั้งจะมีสมการ x = x0.
ตัวอย่าง.
อาการเอียง
เนื่องจากเส้นกำกับเป็นเส้นตรง ถ้าเส้นโค้ง y = เอฟ(x)มีเส้นกำกับเฉียง สมการของมันจะเป็น y = kx + ข. งานของเราคือการหาสัมประสิทธิ์ kและ ข.
ทฤษฎีบท. ตรง y = kx + ขทำหน้าที่เป็นเส้นกำกับเฉียงที่ x→ +∞ สำหรับกราฟของฟังก์ชัน y
= เอฟ(x)ถ้าและเฉพาะถ้า 
. ข้อความที่คล้ายกันนี้เป็นจริงสำหรับ x → –∞.
การพิสูจน์. อนุญาต ส.ส- ความยาวของส่วนเท่ากับระยะทางจากจุด เอ็มไปยังเส้นกำกับ ตามเงื่อนไข. ระบุโดย φ มุมเอียงของเส้นกำกับกับแกน วัว. จากนั้นจาก ΔMNPตามนั้น. เนื่องจาก φ เป็นมุมคงที่ (φ ≠ π/2) ดังนั้น , และ
ด้วยเครื่องคิดเลขออนไลน์ คุณสามารถค้นหา จุดเปลี่ยนเว้าและช่วงนูนของกราฟฟังก์ชันด้วยการออกแบบโซลูชันใน Word ไม่ว่าฟังก์ชันของตัวแปรสองตัว f(x1,x2) จะเป็นนูนหรือไม่ก็ตามโดยใช้เมทริกซ์เฮสเซียน
กฎการป้อนฟังก์ชัน:
ทิศทางความนูนของกราฟของฟังก์ชัน จุดเปลี่ยน
คำนิยาม: เส้นโค้ง y=f(x) เรียกว่า นูนลงในช่วงเวลา (a; b) หากอยู่เหนือแทนเจนต์ ณ จุดใดๆ ของช่วงเวลานี้คำจำกัดความ: เส้นโค้ง y=f(x) เรียกว่า นูนขึ้นในช่วงเวลา (a; b) หากอยู่ใต้เส้นสัมผัส ณ จุดใด ๆ ของช่วงเวลานี้ 
คำนิยาม: ช่วงเวลาที่กราฟของฟังก์ชันนูนขึ้นหรือลงเรียกว่าช่วงเวลาของการนูนของกราฟของฟังก์ชัน
ความนูนขึ้นหรือลงของเส้นโค้ง ซึ่งเป็นกราฟของฟังก์ชัน y=f(x) มีลักษณะเป็นสัญญาณของอนุพันธ์อันดับสองของมัน: ถ้าในช่วงเวลาใดช่วงหนึ่ง f''(x) > 0 แสดงว่าเส้นโค้งนั้นนูน ลงในช่วงเวลานี้; ถ้า f''(x)< 0, то кривая выпукла вверх на этом промежутке.
คำนิยาม: จุดของกราฟของฟังก์ชัน y=f(x) ที่แยกช่วงนูนของทิศทางตรงข้ามของกราฟนี้เรียกว่าจุดเปลี่ยนเว้า 
เฉพาะจุดวิกฤตของประเภทที่สองเท่านั้นที่สามารถทำหน้าที่เป็นจุดเปลี่ยนได้ คะแนนที่เป็นของโดเมนของฟังก์ชัน y = f(x) ซึ่งอนุพันธ์อันดับสอง f''(x) หายไปหรือแตก
กฎการหาจุดเปลี่ยนของกราฟฟังก์ชัน y = f(x)
- หาอนุพันธ์อันดับสอง f''(x)
- ค้นหาจุดวิกฤตของฟังก์ชันประเภทที่สอง y=f(x) เช่น จุดที่ f''(x) หายไปหรือหัก
- ตรวจสอบเครื่องหมายของอนุพันธ์อันดับสอง f''(x) ในช่วงเวลาที่จุดวิกฤตที่พบแบ่งโดเมนของฟังก์ชัน f(x) ถ้าในกรณีนี้ จุดวิกฤต x 0 แยกช่วงนูนของทิศทางตรงกันข้าม x 0 คือ abscissa ของจุดเปลี่ยนเว้าของกราฟฟังก์ชัน
- คำนวณค่าฟังก์ชันที่จุดเปลี่ยน
ตัวอย่างที่ 1 . ค้นหาช่องว่างนูนและจุดเปลี่ยนเว้าของเส้นโค้งต่อไปนี้: f(x) = 6x 2 –x 3
วิธีแก้ปัญหา: ค้นหา f '(x) = 12x - 3x 2 , f ''(x) = 12 - 6x
หาจุดวิกฤตด้วยอนุพันธ์อันดับสองโดยแก้สมการ 12-6x=0 กัน x=2 . 
f(2) = 6*2 2 - 2 3 = 16
คำตอบ: ฟังก์ชันนูนขึ้นสำหรับ x∈(2; +∞) ; ฟังก์ชั่นนูนลงสำหรับ x∈(-∞; 2 ; จุดเปลี่ยน (2;16) .
ตัวอย่างที่ 2 . ฟังก์ชันมีจุดเปลี่ยนหรือไม่: f(x)=x 3 -6x 2 +2x-1
ตัวอย่างที่ 3 . ค้นหาช่วงเวลาที่กราฟฟังก์ชันนูนและนูน: f(x)=x 3 -6x 2 +12x+4
สามารถหาอนุพันธ์ได้บนช่วง (a, c) จากนั้นจะมีแทนเจนต์ของกราฟของฟังก์ชัน ณ จุดใด ๆ 
กราฟนี้ ( 
) และแทนเจนต์ไม่ขนานกับแกน OY เนื่องจากความชันของมันเท่ากับ 
, แน่นอน.
คำนิยาม
บน (a, c) มีการปลดปล่อยชี้ลง (ขึ้น) หากไม่อยู่ต่ำกว่า (ไม่อยู่เหนือ) สัมผัสกับกราฟของฟังก์ชันบน (a, c) 
(
) ในทุกจุดของช่วงเวลานี้ จากนั้นเส้นโค้งที่เป็นกราฟของฟังก์ชันจะนูน (เว้า) ในช่วงเวลานี้
เรียกว่าจุดเปลี่ยนเว้าของกราฟฟังก์ชัน ถ้าอยู่ที่จุด 
กราฟมีแทนเจนต์และมีบริเวณใกล้เคียงของจุดดังกล่าว 
ซึ่งกราฟของฟังก์ชันทางด้านซ้ายและด้านขวาของจุดนั้นมีทิศทางนูนต่างกัน
เป็นที่แน่ชัดว่าที่จุดเปลี่ยน แทนเจนต์ตัดกับกราฟของฟังก์ชัน เนื่องจากด้านหนึ่งของจุดนี้ กราฟจะอยู่เหนือแทนเจนต์ และอีกด้านหนึ่ง - ข้างใต้นั้น นั่นคือ ในบริเวณใกล้เคียงกับจุดเปลี่ยน กราฟของฟังก์ชันจะส่งผ่านทางเรขาคณิตจากด้านหนึ่งของเส้นสัมผัสไปยังอีกด้านหนึ่ง และ "โค้ง" ผ่านมัน นี่คือที่มาของชื่อ "จุดเปลี่ยน"
อนุพันธ์อันดับสองต่อเนื่อง แล้ว 
.
ไม่มีจุดเปลี่ยนที่ (0, 0) แม้ว่า 
ที่ 
. ดังนั้น ความเท่าเทียมกันของอนุพันธ์อันดับสองถึงศูนย์จึงเป็นเพียงเงื่อนไขที่จำเป็นสำหรับการผันแปร 
มันมี 
มีอนุพันธ์อันดับสองในย่านใกล้เคียงของจุด ยกเว้นจุดนั้นเอง และมีแทนเจนต์ของกราฟของฟังก์ชันที่จุด 
. จากนั้น หากภายในย่านที่ระบุ มีสัญญาณต่างกันทางด้านซ้ายและด้านขวาของจุด กราฟของฟังก์ชันจะมีการเปลี่ยนแปลงที่จุด 
ความนูน, ความเว้า, จุดเปลี่ยน 
, 
=
ไม่มีอยู่ที่ 
)
)
หรือใกล้จุดที่ไม่ต่อเนื่องกันของประเภทที่ 2 มักจะปรากฏว่ากราฟของฟังก์ชันเข้าใกล้เส้นตรงเส้นเดียวหรือเส้นอื่นที่ใกล้เคียงที่สุด เส้นดังกล่าวเรียกว่า
คำจำกัดความ 1
เรียกว่าเส้นกำกับของเส้นโค้ง L ถ้าระยะห่างจากจุดของเส้นโค้งถึงเส้นนี้มีแนวโน้มเป็นศูนย์เมื่อจุดเคลื่อนออกไปตามเส้นโค้งจนถึงอนันต์ เส้นกำกับมีสามประเภท: แนวตั้ง, แนวนอน, เฉียง 
เรียกว่าเส้นกำกับแนวดิ่งของกราฟฟังก์ชัน ถ้าขีดจำกัดด้านเดียวอย่างน้อยหนึ่งค่าเท่ากับ 
, กล่าวคือ, หรือ 
มีเส้นกำกับแนวตั้ง 
, เพราะ 
, แ 
.
ถ้า 
.
.
(
) เรียกว่าเส้นกำกับเฉียงของกราฟของฟังก์ชันสำหรับ 
ถ้า 
; 
.
; x=0 – เส้นกำกับแนวตั้ง
.
เป็นเส้นกำกับเฉียง 
และพล็อตมัน 
ฟังก์ชันไม่คู่หรือคี่-
-
+
+
y
-4
ที อาร์
0
บทสรุป.
คุณลักษณะที่สำคัญของวิธีการที่พิจารณาคือขึ้นอยู่กับการตรวจจับและศึกษาคุณลักษณะเฉพาะในพฤติกรรมของเส้นโค้งเป็นหลัก สถานที่ที่ฟังก์ชันเปลี่ยนแปลงไปอย่างราบรื่นจะไม่ได้รับการศึกษาในรายละเอียดโดยเฉพาะ และไม่มีความจำเป็นสำหรับการศึกษาดังกล่าว แต่สถานที่เหล่านั้นที่ฟังก์ชันมีลักษณะเฉพาะใด ๆ จะต้องได้รับการวิจัยอย่างเต็มรูปแบบและการแสดงภาพกราฟิกที่แม่นยำที่สุด คุณลักษณะเหล่านี้คือจุดสูงสุด ต่ำสุด จุดที่ไม่ต่อเนื่องของฟังก์ชัน ฯลฯ
การกำหนดทิศทางของการเว้าและการผันแปรตลอดจนวิธีการระบุในการค้นหาเส้นกำกับทำให้สามารถศึกษาฟังก์ชันโดยละเอียดยิ่งขึ้นและรับแนวคิดเกี่ยวกับกราฟที่แม่นยำยิ่งขึ้น
แนวคิดของการนูนของฟังก์ชัน
พิจารณาฟังก์ชัน \(y = f\left(x \right),\) ซึ่งถือว่าต่อเนื่องในส่วน \(\left[ (a,b) \right].\) ฟังก์ชัน \(y = f \left(x \right),\) )\) เรียกว่า นูนลง (หรือง่ายๆ นูน) ถ้าจุดใด ๆ \((x_1)\) และ \((x_2)\) จาก \(\left[ (a,b) \right]\) x_1),(x_2) \in \left[ (a, b) \right],\) เช่นนั้น \((x_1) \ne (x_2),\) จากนั้นฟังก์ชัน \(f\left(x \right) \) จะถูกเรียก นูนลงอย่างเคร่งครัด
ฟังก์ชันนูนขึ้นมีการกำหนดในทำนองเดียวกัน ฟังก์ชั่น \(f\left(x \right)\) เรียกว่า นูนขึ้น (หรือ เว้า) ถ้าจุดใด ๆ \((x_1)\) และ \((x_2)\) ของส่วน \(\left[ (a,b) \right]\) ความไม่เท่าเทียมกัน \ หากความไม่เท่าเทียมกันนี้เข้มงวดสำหรับใด ๆ \( ( x_1),(x_2) \in \left[ (a,b) \right],\) เช่นนั้น \((x_1) \ne (x_2),\) จากนั้นฟังก์ชัน \(f\left(x \right ) \) เรียกว่า นูนขึ้นอย่างเคร่งครัด บนเซ็กเมนต์ \(\left[ (a,b) \right].\)
การตีความทางเรขาคณิตของการนูนของฟังก์ชัน
คำจำกัดความที่แนะนำของฟังก์ชันนูนมีการตีความทางเรขาคณิตอย่างง่าย
สำหรับฟังก์ชั่น นูนลง (วาด \(1\)) จุดกึ่งกลาง \(B\) ของคอร์ดใด ๆ \((A_1)(A_2)\) อยู่ ข้างบน
ในทำนองเดียวกันสำหรับฟังก์ชัน นูนขึ้น (วาด \(2\)), จุดกึ่งกลาง \(B\) ของคอร์ดใด ๆ \((A_1)(A_2)\) อยู่ ด้านล่างจุดที่สอดคล้องกัน \((A_0)\) ของกราฟของฟังก์ชันหรือตรงกับจุดนี้
ฟังก์ชันนูนมีคุณสมบัติการมองเห็นอื่นซึ่งเกี่ยวข้องกับตำแหน่ง แทนเจนต์ ไปยังกราฟของฟังก์ชัน ฟังก์ชัน \(f\left(x \right)\) is นูนลง บนเซ็กเมนต์ \(\left[ (a,b) \right]\) ถ้ากราฟไม่ต่ำกว่าเส้นสัมผัสที่จุดใด ๆ \((x_0)\) ของเซ็กเมนต์ \(\left [ (a ,b) \right]\) (รูปที่ \(3\))
ดังนั้น ฟังก์ชัน \(f\left(x \right)\) คือ นูนขึ้น บนเซ็กเมนต์ \(\left[ (a,b) \right]\) ถ้ากราฟไม่สูงกว่าเส้นสัมผัสที่จุดใด ๆ \((x_0)\) ของเซ็กเมนต์ \(\left [ (a ,b) \right]\) (รูป \(4\)) คุณสมบัติเหล่านี้เป็นทฤษฎีบทและสามารถพิสูจน์ได้โดยใช้นิยามความนูนของฟังก์ชัน
เงื่อนไขเพียงพอสำหรับการนูน
ให้ฟังก์ชัน \(f\left(x \right)\) อนุพันธ์แรก \(f"\left(x \right)\) มีอยู่ในเซ็กเมนต์ \(\left[ (a,b) \right], \) และอนุพันธ์อันดับสอง \(f""\left(x \right)\) − ในช่วงเวลา \(\left((a,b) \right).\) จากนั้น เกณฑ์ที่เพียงพอสำหรับการคงความนูนดังต่อไปนี้:
ถ้า \(f""\left(x \right) \ge 0\) สำหรับทั้งหมด \(x \in \left((a,b) \right),\) ดังนั้นฟังก์ชัน \(f\left(x \ ขวา )\) นูนลง บนเซ็กเมนต์ \(\left[ (a,b) \right];\)
ถ้า \(f""\left(x \right) \le 0\) สำหรับทั้งหมด \(x \in \left((a,b) \right),\) ดังนั้นฟังก์ชัน \(f\left(x \ ขวา )\) นูนขึ้น บนเซ็กเมนต์ \(\left[ (a,b) \right].\)
ให้เราพิสูจน์ทฤษฎีบทข้างต้นสำหรับกรณีของฟังก์ชันนูนลง ให้ฟังก์ชัน \(f\left(x \right)\) มีอนุพันธ์อันดับสองที่ไม่เป็นลบในช่วงเวลา \(\left((a,b) \right):\) \(f""\left(x \right) \ge 0.\) แทนด้วย \((x_0)\) จุดกึ่งกลางของกลุ่ม \(\left[ ((x_1),(x_2)) \right].\) สมมติว่าความยาวของส่วนนี้ เท่ากับ \(2h.\) จากนั้นพิกัด \((x_1)\) และ \((x_2)\) สามารถเขียนได้ดังนี้: \[(x_1) = (x_0) - h,\;\;(x_2 ) = (x_0) + h.\] ขยายฟังก์ชัน \(f\left(x \right)\) ที่จุด \((x_0)\) ลงในอนุกรมเทย์เลอร์ที่มีพจน์ที่เหลือในรูปแบบลากรองจ์ เราได้รับนิพจน์ต่อไปนี้: \[ (f\left(((x_1))) \right) = f\left(((x_0) - h) \right) ) = (f\left((x_0)) \right ) - f"\left(((x_0)) \right)h + \frac((f""\left(((\xi _1)) \right)(h^2)))((2},}
\]
\[
{f\left({{x_2}} \right) = f\left({{x_0} + h} \right) }
= {f\left({{x_0}} \right) + f"\left({{x_0}} \right)h + \frac{{f""\left({{\xi _2}} \right){h^2}}}{{2!}},}
\]
где \({x_0} - h !}
เพิ่มความเท่าเทียมกันทั้งสอง: \[ (f\left((x_1)) \right) + f\left((x_2)) \right) ) = (2f\left(((x_0)) \right) + \frac (((h^2)))(2)\left[ (f""\left(((\xi _1)) \right) + f""\left(((\xi _2)) \right)) \right].) \] เนื่องจาก \((\xi _1),(\xi _2) \in \left((a,b) \right),\) อนุพันธ์อันดับสองทางด้านขวามือไม่เป็นลบ . ดังนั้น \ หรือ \ นั่นคือตามคำจำกัดความของฟังก์ชัน \(f\left(x \right)\) นูนลง
.
โปรดทราบว่าเงื่อนไขการนูนที่จำเป็นสำหรับฟังก์ชัน (เช่น ทฤษฎีบทโดยตรง เช่น จากเงื่อนไขนูนจะเป็นไปตามที่ \(f""\left(x \right) \ge 0\)) เป็นที่พอใจสำหรับ ความไม่เท่าเทียมกันที่ไม่เข้มงวด ในกรณีของการนูนอย่างเข้มงวด เงื่อนไขที่จำเป็นโดยทั่วไปจะไม่เป็นที่พอใจ ตัวอย่างเช่น ฟังก์ชัน \(f\left(x \right) = (x^4)\) จะนูนลงอย่างเคร่งครัด อย่างไรก็ตาม ณ จุด \(x = 0\) อนุพันธ์อันดับสองมีค่าเท่ากับศูนย์ นั่นคือ ความไม่เท่าเทียมกันอย่างเข้มงวด \(f""\left(x \right) \gt 0\) ไม่พอใจในกรณีนี้
คุณสมบัติของฟังก์ชันนูน
เราแสดงรายการคุณสมบัติบางอย่างของฟังก์ชันนูน สมมติว่าฟังก์ชันทั้งหมดถูกกำหนดและต่อเนื่องบนเซ็กเมนต์ \(\left[ (a,b) \right].\)
หากฟังก์ชัน \(f\) และ \(g\) นูนขึ้น (ขึ้นด้านบน) แสดงว่าฟังก์ชันใด ๆ ชุดค่าผสมเชิงเส้น \(af + bg,\) โดยที่ \(a\), \(b\) เป็นจำนวนจริงบวก และนูนลง (ขึ้นด้านบน)
หากฟังก์ชัน \(u = g\left(x \right)\) นูนลง และฟังก์ชัน \(y = f\left(u \right)\) นูนลงและไม่ลดลง ดังนั้น ฟังก์ชั่นที่ซับซ้อน \(y = f\left((g\left(x \right)) \right)\) จะนูนลงมาเช่นกัน
หากฟังก์ชัน \(u = g\left(x \right)\) นูนขึ้นและฟังก์ชัน \(y = f\left(u \right)\) นูนลงและไม่เพิ่มขึ้น ดังนั้น ฟังก์ชั่นที่ซับซ้อน \(y = f\left((g\left(x \right)) \right)\) จะนูนลง
สูงสุดในพื้นที่ ฟังก์ชันนูนขึ้นที่กำหนดไว้ในส่วน \(\left[ (a,b) \right],\) พร้อมกัน มูลค่าสูงสุด ในส่วนนี้
ขั้นต่ำในท้องถิ่น ฟังก์ชันนูนล่างที่กำหนดไว้ในส่วน \(\left[ (a,b) \right],\) พร้อมกัน ค่าที่น้อยที่สุด ในส่วนนี้
เมื่อเราพล็อตฟังก์ชัน สิ่งสำคัญคือต้องกำหนดช่วงนูนและจุดเปลี่ยนเว้า เราต้องการมันพร้อมกับช่วงเวลาของการลดลงและเพิ่มขึ้นสำหรับการแสดงฟังก์ชันในรูปแบบกราฟิกที่ชัดเจน
การทำความเข้าใจหัวข้อนี้จำเป็นต้องรู้ว่าอนุพันธ์ของฟังก์ชันคืออะไรและจะคำนวณตามลำดับใด ตลอดจนสามารถแก้ไขได้ ประเภทต่างๆความไม่เท่าเทียมกัน
ในตอนต้นของบทความ มีการกำหนดแนวคิดหลัก จากนั้นเราจะแสดงความสัมพันธ์ระหว่างทิศทางของความนูนกับค่าของอนุพันธ์อันดับสองในช่วงเวลาหนึ่ง ต่อไป เราจะระบุเงื่อนไขที่สามารถกำหนดจุดเปลี่ยนเว้าของกราฟได้ การให้เหตุผลทั้งหมดจะแสดงด้วยตัวอย่างการแก้ปัญหา
คำจำกัดความ 1ในทิศทางขาลงในช่วงเวลาหนึ่งในกรณีที่กราฟของมันตั้งอยู่ไม่ต่ำกว่าแทนเจนต์ที่จุดใด ๆ ของช่วงเวลานี้
คำจำกัดความ 2
ฟังก์ชันดิฟเฟอเรนติเอเบิลคือนูนขึ้นไปในช่วงเวลาหนึ่งถ้ากราฟของฟังก์ชันนี้ไม่สูงกว่าค่าสัมผัส ณ จุดใดๆ ของช่วงเวลานี้
ฟังก์ชันนูนลงสามารถเรียกได้ว่าเว้า คำจำกัดความทั้งสองแสดงไว้อย่างชัดเจนในกราฟด้านล่าง:
คำจำกัดความ 3
ฟังก์ชันจุดเปลี่ยนคือจุด M (x 0 ; f (x 0)) ซึ่งมีแทนเจนต์กับกราฟของฟังก์ชัน โดยมีเงื่อนไขว่าอนุพันธ์มีอยู่ในบริเวณใกล้เคียงจุด x 0 โดยที่กราฟของฟังก์ชันใช้ทิศทางต่างกัน นูนออกมาทางด้านซ้ายและขวา
พูดง่ายๆ คือ จุดเปลี่ยนเว้าคือตำแหน่งบนกราฟที่มีแทนเจนต์ และทิศทางของความนูนของกราฟเมื่อผ่านสถานที่นี้จะเปลี่ยนทิศทางของส่วนนูน หากคุณจำไม่ได้ว่าภายใต้เงื่อนไขใดที่การมีอยู่ของแทนเจนต์แนวตั้งและไม่ใช่แนวดิ่งเป็นไปได้ เราขอแนะนำให้คุณทำซ้ำส่วนบนแทนเจนต์ของกราฟของฟังก์ชัน ณ จุดหนึ่ง
ด้านล่างเป็นกราฟของฟังก์ชันที่มีจุดเปลี่ยนหลายจุดเน้นด้วยสีแดง ให้เราชี้แจงว่าไม่จำเป็นต้องมีจุดเปลี่ยน บนกราฟของฟังก์ชันหนึ่ง สามารถมีได้หนึ่ง สอง หลาย อันเป็นอนันต์ หรือไม่มีเลย
ในส่วนนี้ เราจะพูดถึงทฤษฎีบทที่คุณสามารถกำหนดช่วงนูนบนกราฟของฟังก์ชันเฉพาะได้
คำจำกัดความ 4
กราฟของฟังก์ชันจะมีส่วนนูนในทิศทางขึ้นหรือลง หากฟังก์ชันที่สอดคล้องกัน y = f (x) มีอนุพันธ์อันดับสองบนช่วงที่กำหนด x โดยที่อสมการ f "" (x) ≥ 0 ∀ x ∈ X (f "" (x) ≤ 0 ∀ x ∈ X) จะเป็นจริง
เมื่อใช้ทฤษฎีบทนี้ คุณสามารถค้นหาช่วงเวลาของความเว้าและความนูนบนกราฟของฟังก์ชันใดก็ได้ ในการทำเช่นนี้ คุณเพียงแค่ต้องแก้อสมการ f "" (x) ≥ 0 และ f "" (x) ≤ 0 บนโดเมนของฟังก์ชันที่เกี่ยวข้อง
ให้เราชี้แจงว่าจุดเหล่านั้นที่ไม่มีอนุพันธ์อันดับสอง แต่มีการกำหนดฟังก์ชัน y = f (x) ไว้ในช่วงเวลาของการนูนและความเว้า
มาดูตัวอย่างกัน งานเฉพาะวิธีการใช้ทฤษฎีบทนี้อย่างถูกต้อง
ตัวอย่างที่ 1
สภาพ:กำหนดฟังก์ชัน y = x 3 6 - x 2 + 3 x - 1 . กำหนดว่าช่วงใดที่กราฟจะมีส่วนนูนและความเว้า
วิธีการแก้
โดเมนของฟังก์ชันนี้คือเซตของจำนวนจริงทั้งหมด เริ่มจากการคำนวณอนุพันธ์อันดับสองกัน
y "= x 3 6 - x 2 + 3 x - 1" = x 2 2 - 2 x + 3 ⇒ y "" = x 2 2 - 2 x + 3 = x - 2
เราเห็นว่าโดเมนของอนุพันธ์อันดับสองใกล้เคียงกับโดเมนของฟังก์ชัน ดังนั้น ในการระบุช่วงเวลาของการนูน เราจำเป็นต้องแก้อสมการ f "" (x) ≥ 0 และ f "" (x) ≤ 0 .
y "" ≥ 0 ⇔ x - 2 ≥ 0 ⇔ x ≥ 2 y "" ≤ 0 ⇔ x - 2 ≤ 0 ⇔ x ≤ 2
เราได้กราฟของฟังก์ชันที่กำหนดจะมีเว้าบนเซ็กเมนต์[ 2 ; + ∞) และความนูนบนส่วน (- ∞ ; 2 ] .
เพื่อความชัดเจน เราจะวาดกราฟของฟังก์ชันและทำเครื่องหมายส่วนที่นูนเป็นสีน้ำเงินบนนั้น และส่วนที่เว้าเป็นสีแดง
ตอบ:กราฟของฟังก์ชันที่กำหนดจะมีความเว้าบนเซ็กเมนต์ [2 ; + ∞) และความนูนบนส่วน (- ∞ ; 2 ] .
แต่จะทำอย่างไรถ้าโดเมนของอนุพันธ์อันดับสองไม่ตรงกับโดเมนของฟังก์ชัน? ข้อสังเกตข้างต้นมีประโยชน์สำหรับเรา: จุดที่ไม่มีอนุพันธ์อันดับสองสุดท้าย เราจะรวมในส่วนความเว้าและความนูนด้วย
ตัวอย่าง 2
สภาพ:ให้ฟังก์ชัน y = 8 x x - 1 . กำหนดว่าช่วงใดที่กราฟจะเว้าและในช่วงเวลาใดที่กราฟจะนูน
วิธีการแก้
ก่อนอื่น มาดูขอบเขตของฟังก์ชันกันก่อน
x ≥ 0 x - 1 ≠ 0 ⇔ x ≥ 0 x ≠ 1 ⇔ x ∈ [ 0 ; 1) ∪ (1 ; + ∞)
ตอนนี้เราคำนวณอนุพันธ์อันดับสอง:
y "= 8 x x - 1" = 8 1 2 x (x - 1) - x 1 (x - 1) 2 = - 4 x + 1 x (x - 1) 2 y "" = - 4 x + 1 x (x - 1) 2 "= - 4 1 x x - 1 2 - (x + 1) x x - 1 2" x (x - 1) 4 = = - 4 1 x x - 1 2 - x + 1 1 2 x ( x - 1) 2 + x 2 (x - 1) x x - 1 4 = = 2 3 x 2 + 6 x - 1 x 3 2 (x - 1) 3
โดเมนของอนุพันธ์อันดับสองคือเซต x ∈ (0 ; 1) ∪ (1 ; + ∞) เราจะเห็นว่า x เท่ากับศูนย์จะอยู่ในโดเมนของฟังก์ชันดั้งเดิม แต่ไม่อยู่ในโดเมนของอนุพันธ์อันดับสอง จุดนี้ต้องรวมอยู่ในส่วนของเว้าหรือนูน
หลังจากนั้น เราต้องแก้อสมการ f "" (x) ≥ 0 และ f "" (x) ≤ 0 บนโดเมนของฟังก์ชันที่กำหนด เราใช้วิธีช่วงเวลาสำหรับสิ่งนี้: ที่ x \u003d - 1 - 2 3 3 ≈ - 2, 1547 หรือ x \u003d - 1 + 2 3 3 ≈ 0, 1547 ตัวเศษ 2 (3 x 2 + 6 x - 1) x 2 3 x - 1 3 กลายเป็น 0 และตัวส่วนจะเป็น 0 เมื่อ x เป็นศูนย์หรือหนึ่ง
มาใส่จุดที่เป็นผลลัพธ์บนกราฟและกำหนดเครื่องหมายของนิพจน์ในทุกช่วงที่จะรวมอยู่ในโดเมนของฟังก์ชันดั้งเดิม บนกราฟ พื้นที่นี้แสดงโดยการฟักไข่ หากค่าเป็นบวก ให้ทำเครื่องหมายช่วงเวลาด้วยเครื่องหมายบวก หากเป็นค่าลบ ตามด้วยเครื่องหมายลบ
เพราะเหตุนี้,
f "" (x) ≥ 0 x ∈ [ 0 ; 1) ∪ (1 ; + ∞) ⇔ x ∈ 0 ; - 1 + 2 3 3 ∪ (1 ; + ∞) และ f "" (x) ≤ 0 x ∈ [ 0 ; 1) ∪ (1 ; + ∞) ⇔ x ∈ [ - 1 + 2 3 3 ; หนึ่ง)
เราเปิดจุดที่ทำเครื่องหมายไว้ก่อนหน้านี้ x = 0 และรับคำตอบที่ต้องการ กราฟของฟังก์ชันเดิมจะมีส่วนนูนลงที่ 0 ; - 1 + 2 3 3 ∪ (1 ; + ∞) และสูงกว่า - สำหรับ x ∈ [ - 1 + 2 3 3 ; หนึ่ง) .
ลองวาดกราฟ ทำเครื่องหมายส่วนที่นูนเป็นสีน้ำเงิน และเว้าเป็นสีแดง เส้นกำกับแนวตั้งทำเครื่องหมายด้วยเส้นประสีดำ
ตอบ:กราฟของฟังก์ชันเดิมจะมีส่วนนูนลงที่ 0 ; - 1 + 2 3 3 ∪ (1 ; + ∞) และสูงกว่า - สำหรับ x ∈ [ - 1 + 2 3 3 ; หนึ่ง) .
เงื่อนไขการผันแปรของกราฟฟังก์ชัน
เริ่มจากการกำหนดเงื่อนไขที่จำเป็นสำหรับการผันแปรของกราฟของฟังก์ชันบางอย่าง
คำจำกัดความ 5
สมมติว่าเรามีฟังก์ชัน y = f(x) ซึ่งกราฟมีจุดเปลี่ยนเว้า สำหรับ x = x 0 มันมีอนุพันธ์อันดับสองที่ต่อเนื่องกัน ดังนั้น f "" (x 0) = 0 จะคงค่าเท่ากัน
จากเงื่อนไขนี้ เราควรมองหาจุดเปลี่ยนเว้าระหว่างจุดที่อนุพันธ์อันดับสองเปลี่ยนเป็น 0 เงื่อนไขนี้จะไม่เพียงพอ: ไม่ใช่ประเด็นทั้งหมดที่จะเหมาะกับเรา
นอกจากนี้ โปรดทราบด้วยว่า ตามคำจำกัดความทั่วไป เราจะต้องมีเส้นสัมผัสกัน แนวตั้งหรือไม่ใช่แนวตั้ง ในทางปฏิบัติ นี่หมายความว่าในการหาจุดเปลี่ยน เราควรหาจุดที่อนุพันธ์อันดับสองของฟังก์ชันนี้กลายเป็น 0 ดังนั้น ในการค้นหา abscissas ของจุดเปลี่ยน เราจำเป็นต้องนำ x 0 ทั้งหมดจากโดเมนของฟังก์ชัน โดยที่ lim x → x 0 - 0 f " (x) = ∞ และ lim x → x 0 + 0 f " (x) = ∞ . ส่วนใหญ่ จุดเหล่านี้คือจุดที่ตัวส่วนของอนุพันธ์อันดับ 1 เปลี่ยนเป็น 0
เงื่อนไขแรกเพียงพอสำหรับการมีอยู่ของจุดเปลี่ยนเว้าของกราฟฟังก์ชัน
เราพบค่า x 0 ทั้งหมดที่สามารถนำมาเป็น abscissa ของจุดผันแปรได้ หลังจากนั้นเราต้องใช้เงื่อนไขการผันแปรที่เพียงพอก่อน
คำจำกัดความ 6
สมมติว่าเรามีฟังก์ชัน y = f (x) ที่ต่อเนื่องที่จุด M (x 0 ; f (x 0)) ยิ่งไปกว่านั้น มันมีแทนเจนต์ ณ จุดนี้ และฟังก์ชันเองก็มีอนุพันธ์อันดับสองในบริเวณใกล้เคียงจุดนี้ x 0 . ในกรณีนี้ หากอนุพันธ์อันดับสองได้เครื่องหมายตรงข้ามทางด้านซ้ายและด้านขวา จุดนี้ก็ถือได้ว่าเป็นจุดเปลี่ยนเว้า
เราเห็นว่าเงื่อนไขนี้ไม่ต้องการอนุพันธ์อันดับสองที่จำเป็นต้องมีอยู่ ณ จุดนี้ การมีอยู่ของมันในละแวกใกล้เคียงของจุด x 0 ก็เพียงพอแล้ว
ทั้งหมดข้างต้นสามารถนำเสนอได้อย่างสะดวกเป็นลำดับของการกระทำ
- ก่อนอื่นคุณต้องหาจุดเปลี่ยนที่เป็นไปได้ทั้งหมด x 0 โดยที่ f "" (x 0) = 0, lim x → x 0 - 0 f "(x) = ∞, lim x → x 0 + 0 f " (x) = ∞ .
- ค้นหาว่าอนุพันธ์จะเปลี่ยนเครื่องหมาย ณ จุดใด ค่าเหล่านี้คือ abscissas ของจุดเปลี่ยนเว้าและจุด M (x 0 ; f (x 0)) ที่สอดคล้องกับค่าเหล่านี้คือจุดเปลี่ยนเอง
เพื่อความชัดเจน ลองพิจารณาปัญหาสองประการ
ตัวอย่างที่ 3
สภาพ:กำหนดฟังก์ชัน y = 1 10 x 4 12 - x 3 6 - 3 x 2 + 2 x . กำหนดว่ากราฟของฟังก์ชันนี้จะมีจุดโค้งและจุดนูนอยู่ที่ใด
วิธีการแก้
ฟังก์ชันนี้ถูกกำหนดบนชุดของจำนวนจริงทั้งหมด เราพิจารณาอนุพันธ์อันดับแรก:
y "= 1 10 x 4 12 - x 3 6 - 3 x 2 + 2 x" = 1 10 4 x 3 12 - 3 x 2 6 - 6 x + 2 = = 1 10 x 3 3 - x 2 2 - 6 x + 2
ทีนี้ลองหาโดเมนของอนุพันธ์อันดับแรกกัน เป็นเซตของจำนวนจริงทั้งหมดด้วย ดังนั้นความเท่าเทียมกัน lim x → x 0 - 0 f "(x) = ∞ และ lim x → x 0 + 0 f" (x) = ∞ ไม่เป็นที่น่าพอใจสำหรับค่าใด ๆ ของ x 0 .
เราคำนวณอนุพันธ์อันดับสอง:
y "" = = 1 10 x 3 3 - x 2 2 - 6 x + 2 " = 1 10 3 x 2 3 - 2 x 2 - 6 = 1 10 x 2 - x - 6
y "" = 0 ⇔ 1 10 (x 2 - x - 6) = 0 ⇔ x 2 - x - 6 = 0 D = (- 1) 2 - 4 1 (- 6) = 25 x 1 = 1 - 25 2 \u003d - 2, x 2 \u003d 1 + 25 2 \u003d 3
เราพบจุดเปลี่ยนที่น่าจะเป็นไปได้สองจุด - 2 และ 3 สิ่งที่เราต้องทำคือตรวจสอบว่าอนุพันธ์เปลี่ยนเครื่องหมาย ณ จุดใด ลองวาดแกนตัวเลขและพล็อตจุดเหล่านี้ หลังจากนั้นเราจะวางเครื่องหมายของอนุพันธ์อันดับสองในช่วงเวลาผลลัพธ์
ส่วนโค้งแสดงทิศทางความนูนของกราฟในแต่ละช่วง
อนุพันธ์อันดับสองกลับเครื่องหมาย (จากบวกเป็นลบ) ที่จุดที่มี abscissa 3 ผ่านจากซ้ายไปขวาและทำเช่นเดียวกัน (จากลบเป็นบวก) ที่จุดด้วย abscissa 3 ดังนั้น เราสามารถสรุปได้ว่า x = - 2 และ x = 3 เป็น abscissas ของจุดเปลี่ยนเว้าของกราฟฟังก์ชัน พวกเขาจะสอดคล้องกับจุดของกราฟ - 2; - 4 3 และ 3 ; - 15 8 .
เรามาดูรูปภาพของแกนตัวเลขอีกครั้งและเครื่องหมายผลลัพธ์บนช่วงเวลาเพื่อสรุปเกี่ยวกับตำแหน่งเว้าและส่วนนูน ปรากฎว่าส่วนนูนจะอยู่ที่ส่วน - 2; 3 และเว้าบนเซ็กเมนต์ (- ∞ ; - 2 ] และ [ 3 ; + ∞)
วิธีแก้ปัญหาแสดงไว้อย่างชัดเจนบนกราฟ: สีน้ำเงิน - ความนูน, สีแดง - ความเว้า, สีดำหมายถึงจุดเปลี่ยน
ตอบ:ส่วนนูนจะอยู่ที่ส่วน - 2; 3 และเว้าบนเซ็กเมนต์ (- ∞ ; - 2 ] และ [ 3 ; + ∞)
ตัวอย่างที่ 4
สภาพ:คำนวณ abscissas ของจุดเปลี่ยนทั้งหมดของกราฟของฟังก์ชัน y = 1 8 · x 2 + 3 x + 2 · x - 3 3 5 .
วิธีการแก้
โดเมนของฟังก์ชันที่กำหนดคือเซตของจำนวนจริงทั้งหมด เราคำนวณอนุพันธ์:
y "= 1 8 (x 2 + 3 x + 2) x - 3 3 5" = = 1 8 x 2 + 3 x + 2 " (x - 3) 3 5 + (x 2 + 3 x + 2) x - 3 3 5 " = = 1 8 2 x + 3 (x - 3) 3 5 + (x 2 + 3 x + 2) 3 5 x - 3 - 2 5 = 13 x 2 - 6 x - 39 40 (x - 3) 2 5
ไม่เหมือนกับฟังก์ชัน อนุพันธ์อันดับแรกจะไม่ถูกกำหนดที่ค่า x เท่ากับ 3 แต่:
ลิม x → 3 - 0 y "(x) = 13 (3 - 0) 2 - 6 (3 - 0) - 39 40 3 - 0 - 3 2 5 = + ∞ ลิม x → 3 + 0 y " (x) = 13 (3 + 0) 2 - 6 (3 + 0) - 39 40 3 + 0 - 3 2 5 = + ∞
ซึ่งหมายความว่าเส้นสัมผัสแนวตั้งของกราฟจะผ่านจุดนี้ ดังนั้น 3 สามารถเป็น abscissa ของจุดเปลี่ยนได้
เราคำนวณอนุพันธ์อันดับสอง นอกจากนี้เรายังพบพื้นที่ของคำจำกัดความและจุดที่เปลี่ยนเป็น 0:
y "" = 13 x 2 - 6 x - 39 40 x - 3 2 5 " = = 1 40 13 x 2 - 6 x - 39 " (x - 3) 2 5 - 13 x 2 - 6 x - 39 x - 3 2 5 " (x - 3) 4 5 = = 1 25 13 x 2 - 51 x + 21 (x - 3) 7 5 , x ∈ (- ∞ ; 3) ∪ (3 ; + ∞ ) y "" ( x) = 0 ⇔ 13 x 2 - 51 x + 21 = 0 D = (- 51) 2 - 4 13 21 = 1509 x 1 = 51 + 1509 26 ≈ 3 , 4556 , x 2 = 51 - 1509 26 ≈ 0.4675
เรามีจุดเปลี่ยนที่เป็นไปได้อีกสองจุด เราวางทั้งหมดบนเส้นจำนวนและทำเครื่องหมายช่วงเวลาผลลัพธ์ด้วยเครื่องหมาย:
การเปลี่ยนแปลงของเครื่องหมายจะเกิดขึ้นเมื่อผ่านแต่ละจุดที่กำหนด ซึ่งหมายความว่าเป็นจุดเปลี่ยนทั้งหมด
ตอบ:ลองวาดกราฟของฟังก์ชัน ทำเครื่องหมายส่วนเว้าเป็นสีแดง ส่วนนูนเป็นสีน้ำเงิน และจุดเปลี่ยนเว้าเป็นสีดำ
เมื่อทราบเงื่อนไขการผันแปรที่เพียงพอครั้งแรก เราสามารถกำหนดจุดที่จำเป็นโดยไม่จำเป็นต้องมีอนุพันธ์อันดับสอง จากนี้เงื่อนไขแรกถือได้ว่าเป็นสากลมากที่สุดและเหมาะสำหรับการแก้ปัญหาประเภทต่างๆ
โปรดทราบว่ามีเงื่อนไขการผันแปรอีกสองเงื่อนไข แต่สามารถใช้ได้เมื่อมีอนุพันธ์ จำกัด ที่จุดที่ระบุเท่านั้น
ถ้าเรามี f "" (x 0) = 0 และ f """ (x 0) ≠ 0 แล้ว x 0 จะเป็น abscissa ของจุดเปลี่ยนเว้าของกราฟ y = f (x)
ตัวอย่างที่ 5
สภาพ:ฟังก์ชัน y = 1 60 x 3 - 3 20 x 2 + 7 10 x - 2 5 ตรวจสอบว่ากราฟฟังก์ชันจะมีการผันผวนที่จุดที่ 3 หรือไม่ 4 5 .
วิธีการแก้
สิ่งแรกที่ต้องทำคือต้องแน่ใจว่าจุดที่กำหนดจะเป็นของกราฟของฟังก์ชันนี้เลย
y (3) = 1 60 3 3 - 3 20 3 2 - 2 5 = 27 60 - 27 20 + 21 10 - 2 5 = 9 - 27 + 42 - 8 20 = 4 5
ฟังก์ชันที่ระบุถูกกำหนดไว้สำหรับอาร์กิวเมนต์ทั้งหมดที่เป็นจำนวนจริง เราคำนวณอนุพันธ์อันดับหนึ่งและสอง:
y "= 1 60 x 3 - 3 20 x 2 + 7 10 x - 2 5" = 1 20 x 2 - 3 10 x + 7 10 y "" = 1 20 x 2 - 3 10 x + 7 10" = 1 10 x - 3 10 = 1 10 (x - 3)
เราได้อนุพันธ์อันดับสองไปที่ 0 ถ้า x เท่ากับ 0 ซึ่งหมายความว่าจะเป็นไปตามเงื่อนไขการเปลี่ยนแปลงที่จำเป็นสำหรับจุดนี้ ตอนนี้เราใช้เงื่อนไขที่สอง: เราหาอนุพันธ์อันดับสามและหาว่ามันจะเปลี่ยนเป็น 0 ที่ 3:
y " " " = 1 10 (x - 3) " = 1 10
อนุพันธ์อันดับสามจะไม่หายไปสำหรับค่าใดๆ ของ x ดังนั้นเราจึงสรุปได้ว่าจุดนี้จะเป็นจุดเปลี่ยนของกราฟของฟังก์ชัน
ตอบ:ขอแสดงวิธีแก้ปัญหาในภาพประกอบ:
สมมติว่า f "(x 0) = 0, f "" (x 0) = 0, . . . , f (n) (x 0) = 0 และ f (n + 1) (x 0) ≠ 0 . ในกรณีนี้ สำหรับแม้แต่ n เราพบว่า x 0 คือ abscissa ของจุดเปลี่ยนเว้าของกราฟ y \u003d f (x) .
ตัวอย่างที่ 6
สภาพ:ให้ฟังก์ชัน y = (x - 3) 5 + 1 . คำนวณจุดเปลี่ยนของกราฟ
วิธีการแก้
ฟังก์ชันนี้ถูกกำหนดบนชุดของจำนวนจริงทั้งหมด คำนวณอนุพันธ์: y " = ((x - 3) 5 + 1) " = 5 x - 3 4 . เนื่องจากมันจะถูกกำหนดให้กับค่าจริงทั้งหมดของอาร์กิวเมนต์ ดังนั้น ณ จุดใด ๆ ในกราฟจะมีแทนเจนต์ที่ไม่ใช่แนวตั้ง
ทีนี้ลองคำนวณว่าค่าอนุพันธ์อันดับสองจะเปลี่ยนเป็น 0 อะไร:
y "" = 5 (x - 3) 4 " = 20 x - 3 3 y "" = 0 ⇔ x - 3 = 0 ⇔ x = 3
เราพบว่าสำหรับ x = 3 กราฟของฟังก์ชันอาจมีจุดเปลี่ยนเว้า เราใช้เงื่อนไขที่สามเพื่อยืนยันสิ่งนี้:
y " " " = 20 (x - 3) 3 " = 60 x - 3 2 , y " " " (3) = 60 3 - 3 2 = 0 y (4) = 60 (x - 3) 2" = 120 (x - 3) , y (4) (3) = 120 (3 - 3) = 0 y (5) = 120 (x - 3) " = 120 , y (5) (3) = 120 ≠ 0
เรามี n = 4 โดยเงื่อนไขเพียงพอที่สาม นี่คือจำนวนคู่ ดังนั้น x \u003d 3 จะเป็น abscissa ของจุดเปลี่ยนเว้าและจุดของกราฟของฟังก์ชัน (3; 1) จะสอดคล้องกับมัน
ตอบ:นี่คือกราฟของฟังก์ชันนี้โดยมีจุดนูน ความเว้า และจุดเปลี่ยนเว้า:
หากคุณสังเกตเห็นข้อผิดพลาดในข้อความ โปรดไฮไลต์แล้วกด Ctrl+Enter