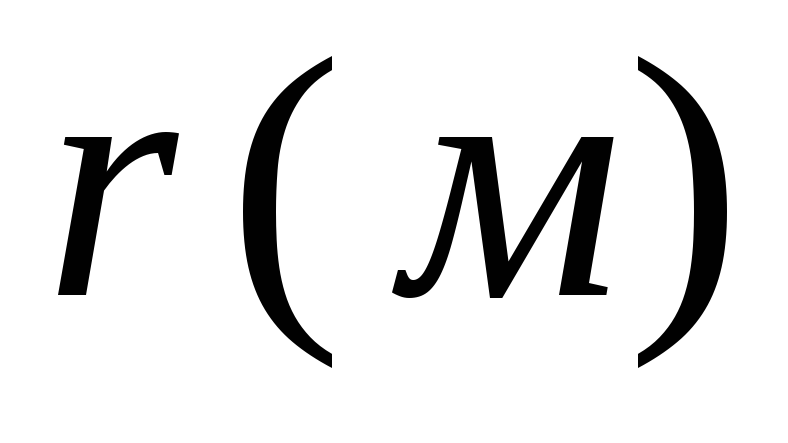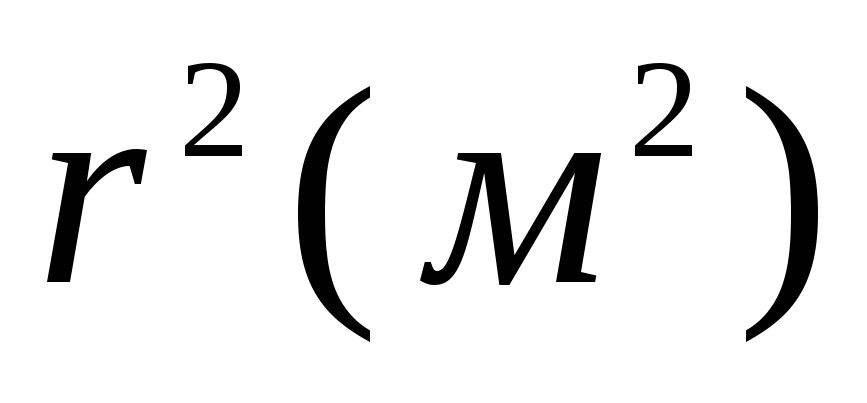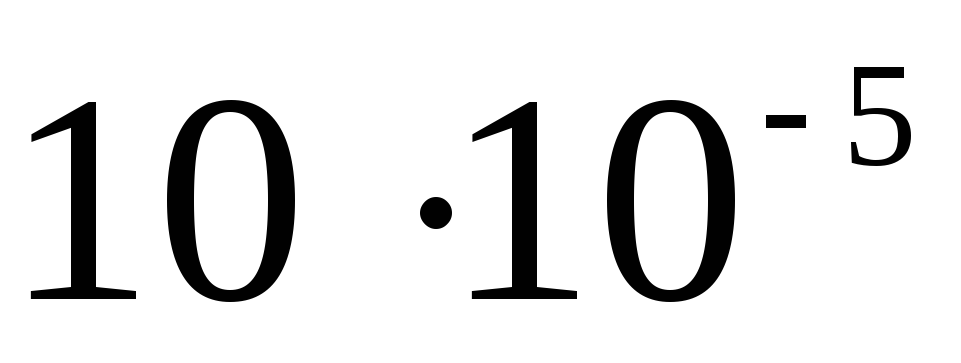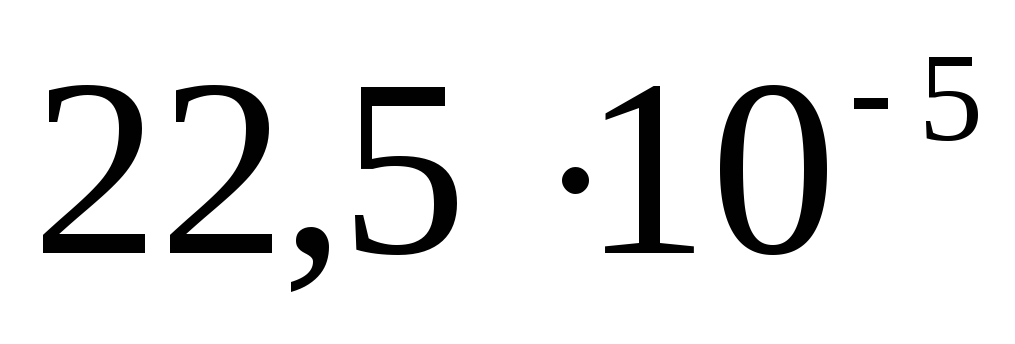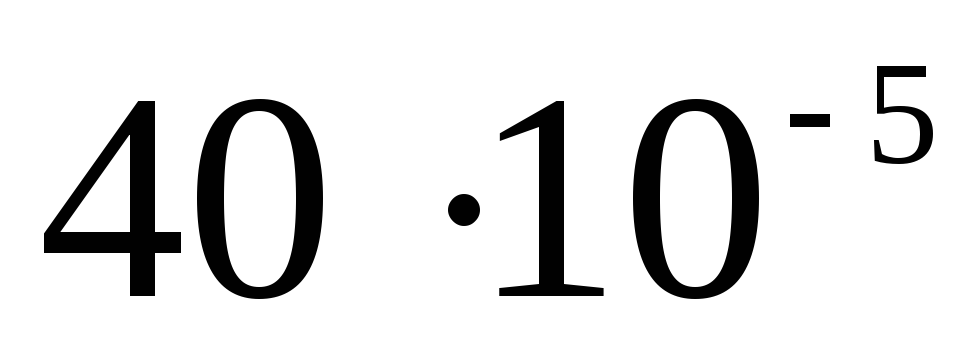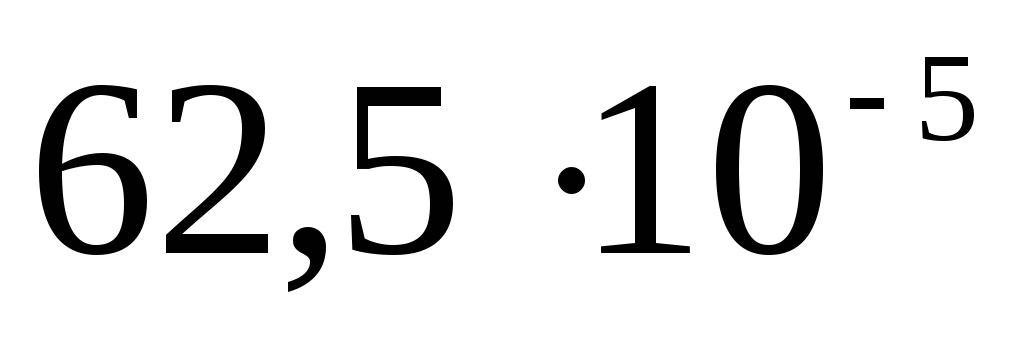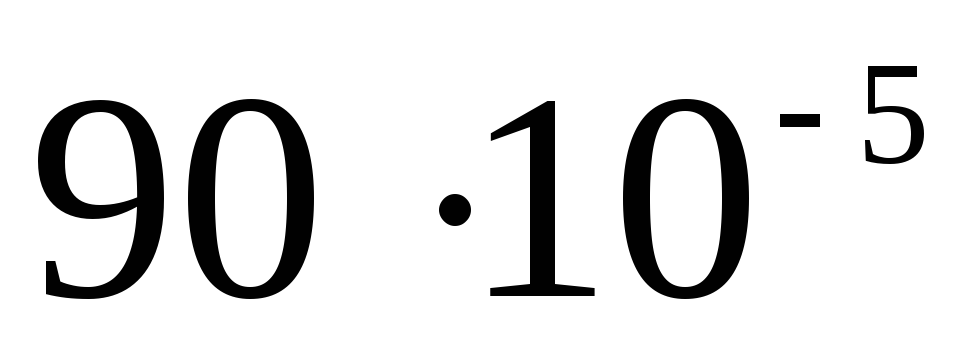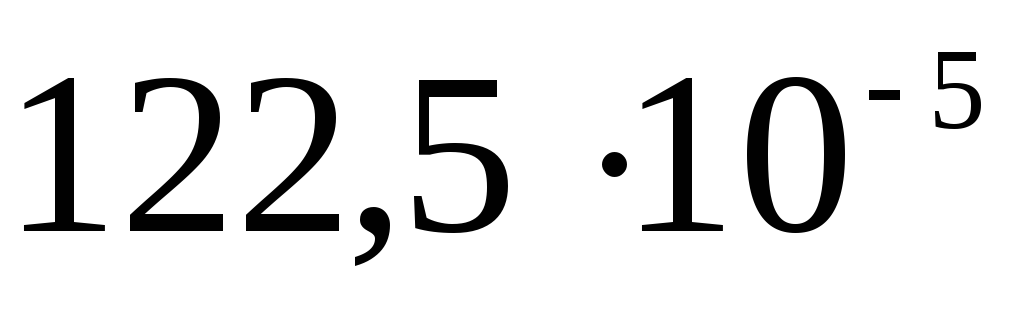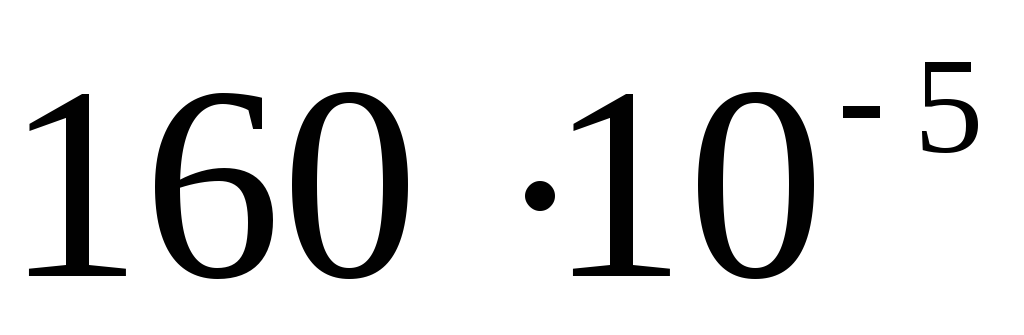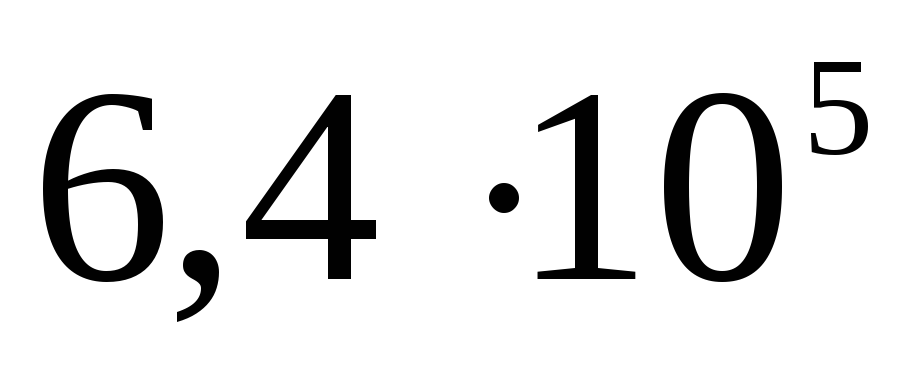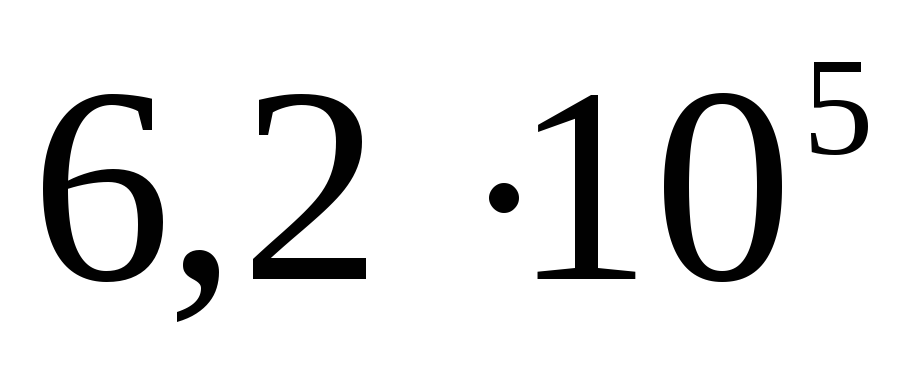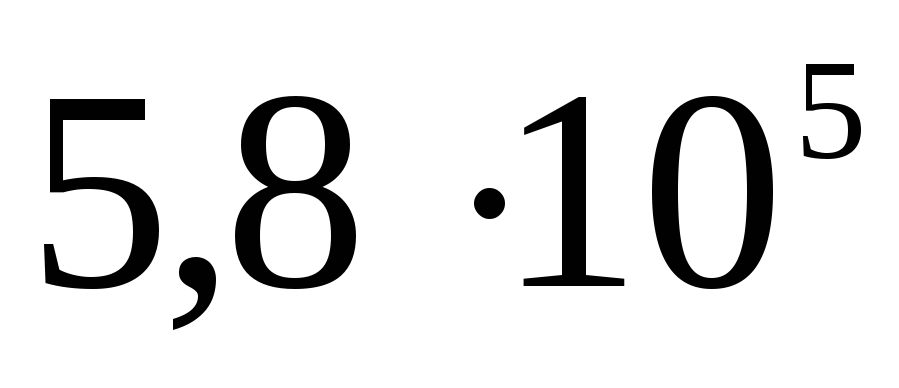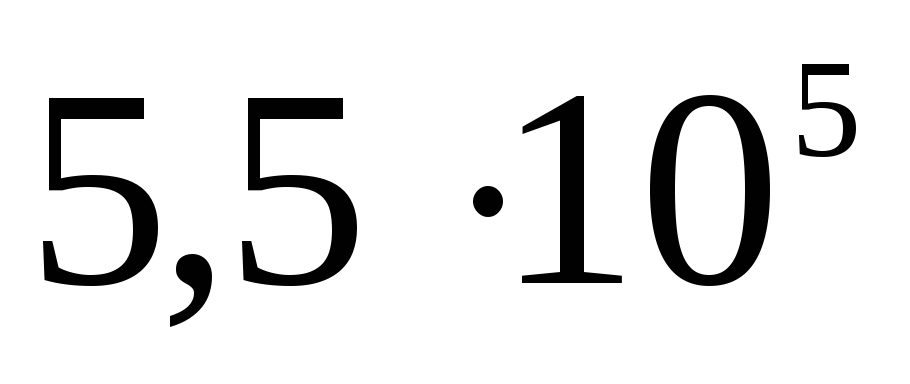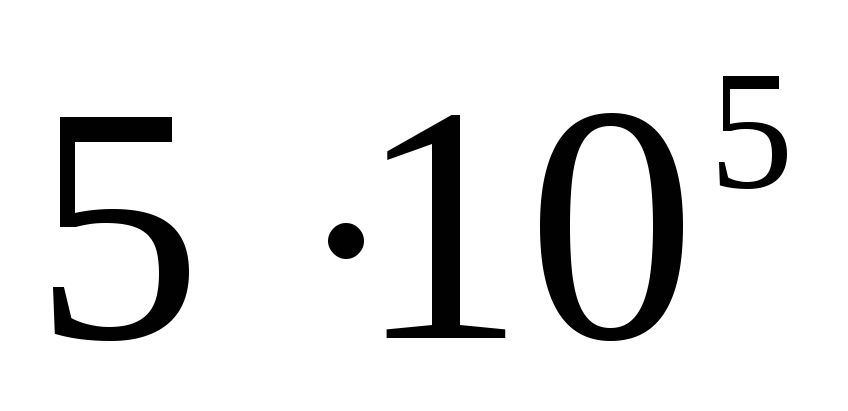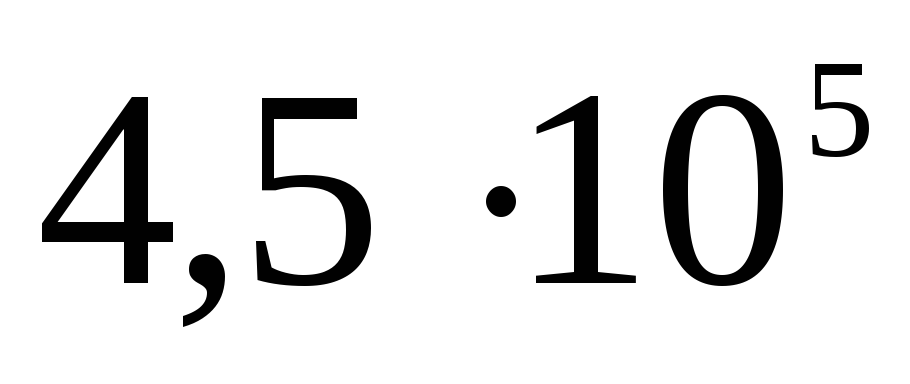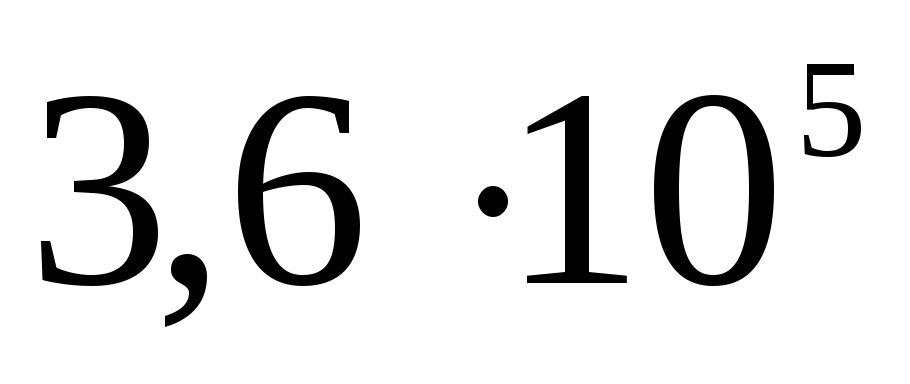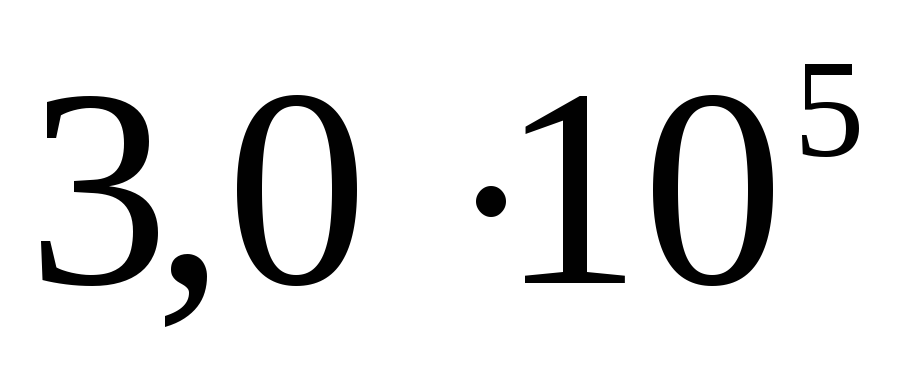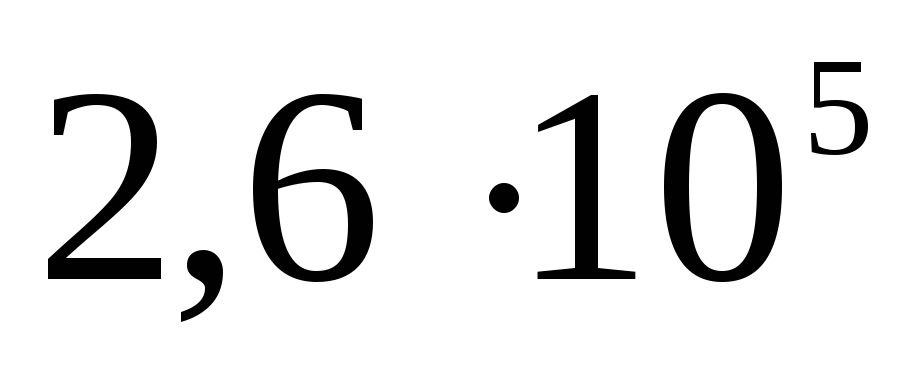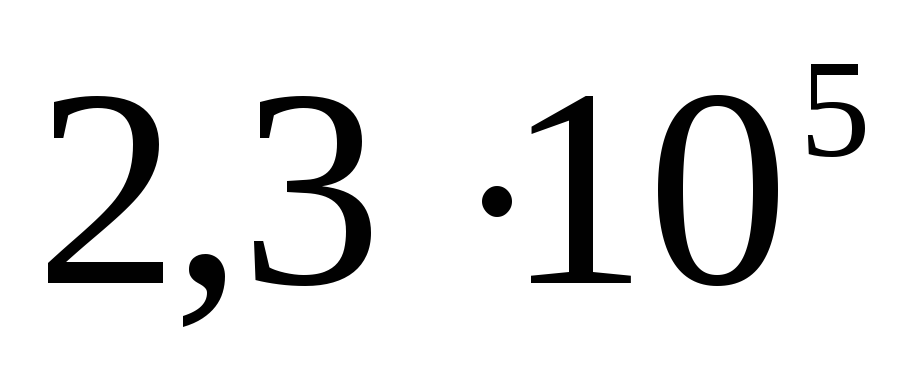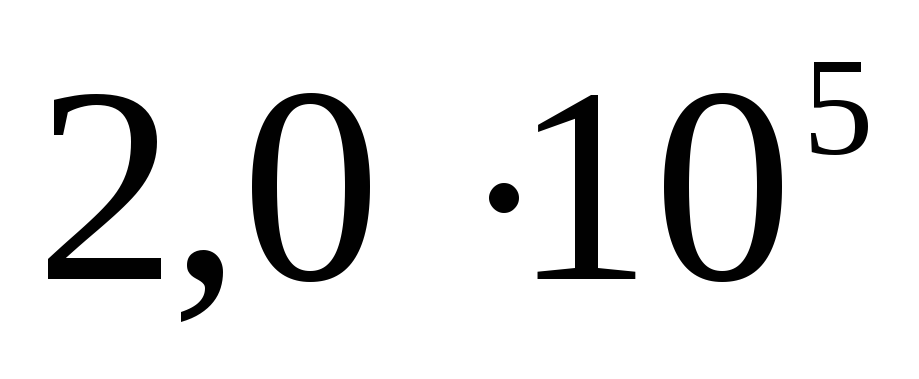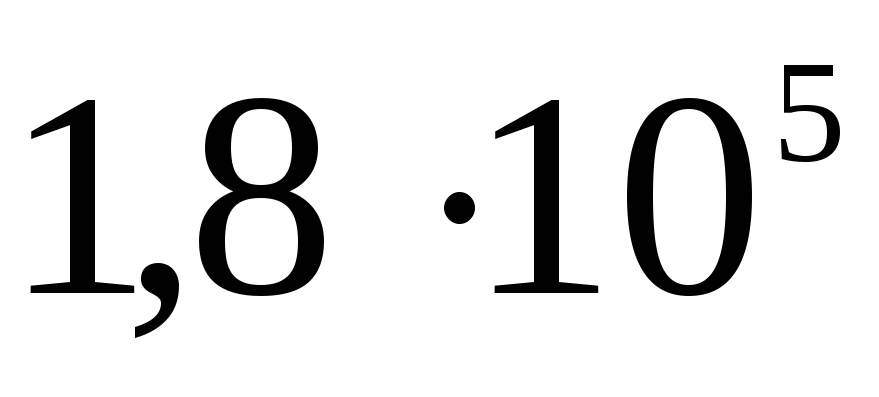Електростатика
1
(ЦТ 2001 Тест 9. А19). Провідна куля радіусу R
має позитивний заряд +
q
. Якщо на відстані 2 Rвід центру кулі помістити точковий негативний заряд –2 q, то потенціал у центрі кулі
Типова помилкапри вирішенні походить з неправильного тлумачення формулювання: «поле всередині провідної кулі відсутнє». З цього твердження робиться хибний висновок: обидві властивості поля: і напруженість, і потенціал – дорівнюють нулю. Насправді у разі нулю дорівнює лише напруженість поля, т.к. вільні заряди перестають переміщатися поверхнею провідника тоді, коли вектор 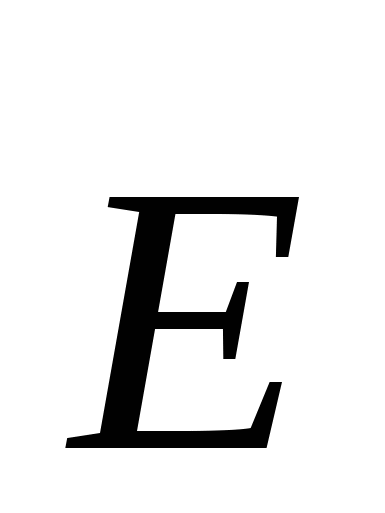 у будь-якій точці поверхні перпендикулярний їй. Поверхня провідника в цьому випадку є еквіпотенційною. Робота переміщення пробного заряду обсягом, обмеженому поверхнею, дорівнює нулю, т.к. дорівнює нулю сила, що діє на заряд; з цього випливає, що потенційна енергія заряду при переміщенні від точки до точки не змінюється: електричний потенціалв обсязі, обмеженому провідною поверхнею, постійний і дорівнює потенціалу на самій поверхні. Зміна напруженості та потенціалу зарядженої сфери з відстанню від центру заряду можна проілюструвати графіками (див. рис.).
у будь-якій точці поверхні перпендикулярний їй. Поверхня провідника в цьому випадку є еквіпотенційною. Робота переміщення пробного заряду обсягом, обмеженому поверхнею, дорівнює нулю, т.к. дорівнює нулю сила, що діє на заряд; з цього випливає, що потенційна енергія заряду при переміщенні від точки до точки не змінюється: електричний потенціалв обсязі, обмеженому провідною поверхнею, постійний і дорівнює потенціалу на самій поверхні. Зміна напруженості та потенціалу зарядженої сфери з відстанню від центру заряду можна проілюструвати графіками (див. рис.).
Рішення
Потенціал, що створюється сферично-симетрично розподіленим зарядом qв центрі кулі, такий же, як на її поверхні і дорівнює φ 1 = q/4 πε 0 R; потенціал, створюваний у цій самій точці точковим зарядом –2 q , розташованим поза сферою на відстані 2 R від її центру, дорівнює φ 2 = – 2 q/4 πε 0 2 R; потенціал у центрі кулі – результат суперпозиції двох полів, тобто. φ = φ 1 + φ 2 = q/4 πε 0 R–2 q/4 πε 0 2 R= 0 .
При виконанні тестових завданьзручно зробити запис якомога коротшим. Наприклад, у цьому випадку достатньо одного загального рівняння φ = q/4 πε 0 r.
Т.к. точковий негативний заряд вдвічі більше заряду, розподіленого на сфері і знаходиться від центру сфери вдвічі далі, із записаного рівняння видно, що потенціали обох зарядів рівні за величиною і протилежні за знаком, отже, результуючий потенціал дорівнює 0.
2 (ЦТ 2001 Тест 11. А 19).
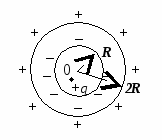 Всередині шарового металевого шару, внутрішній і зовнішній радіуси якого відповідного рівні R
і 2
R
,
на відстані R/
2
q
.
Потенціал у центрі сфери дорівнює…
Всередині шарового металевого шару, внутрішній і зовнішній радіуси якого відповідного рівні R
і 2
R
,
на відстані R/
2
q
.
Потенціал у центрі сфери дорівнює…
Рішення
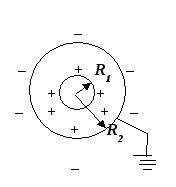
Труднощівикликає побудову картини розподілу зарядів на поверхнях шарового шару.
Завдяки електростатичній індукції на внутрішній поверхні сфери з'являється заряд –
q
, а на зовнішній + q
.
Потенціал у центрі сфери 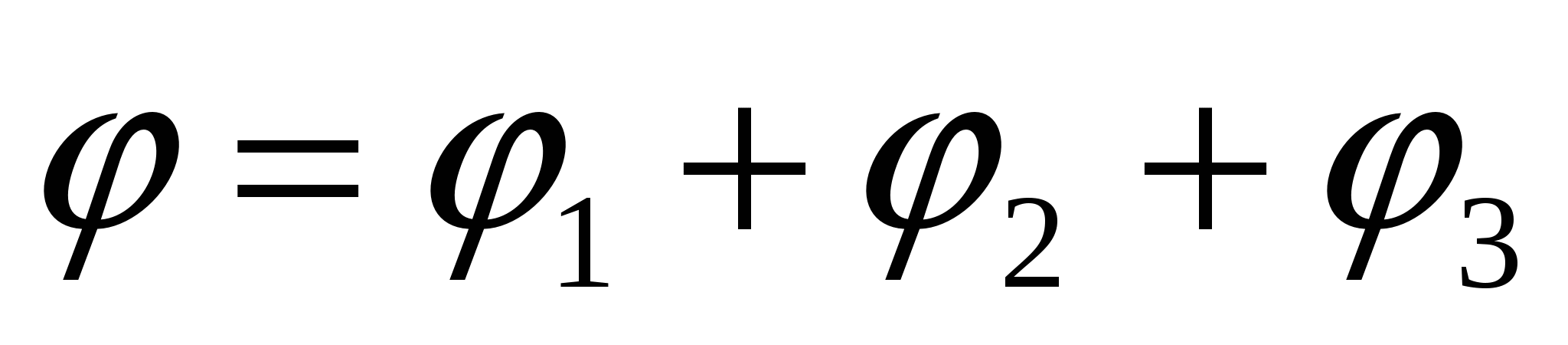 ;
;
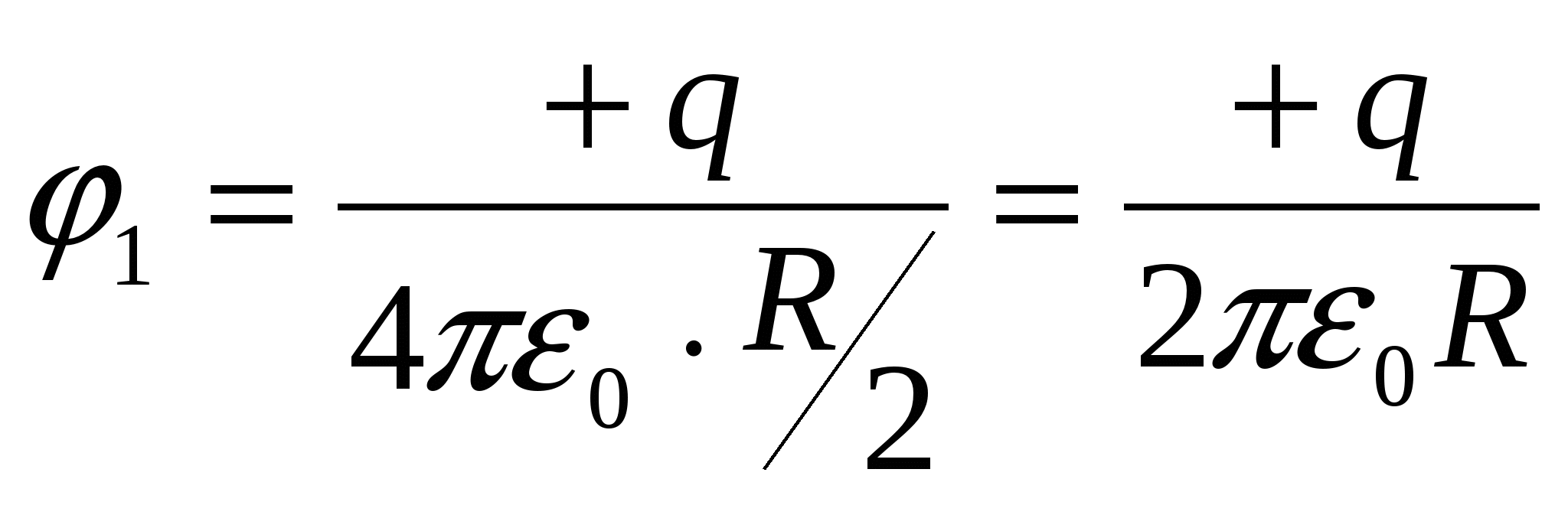 ;
; 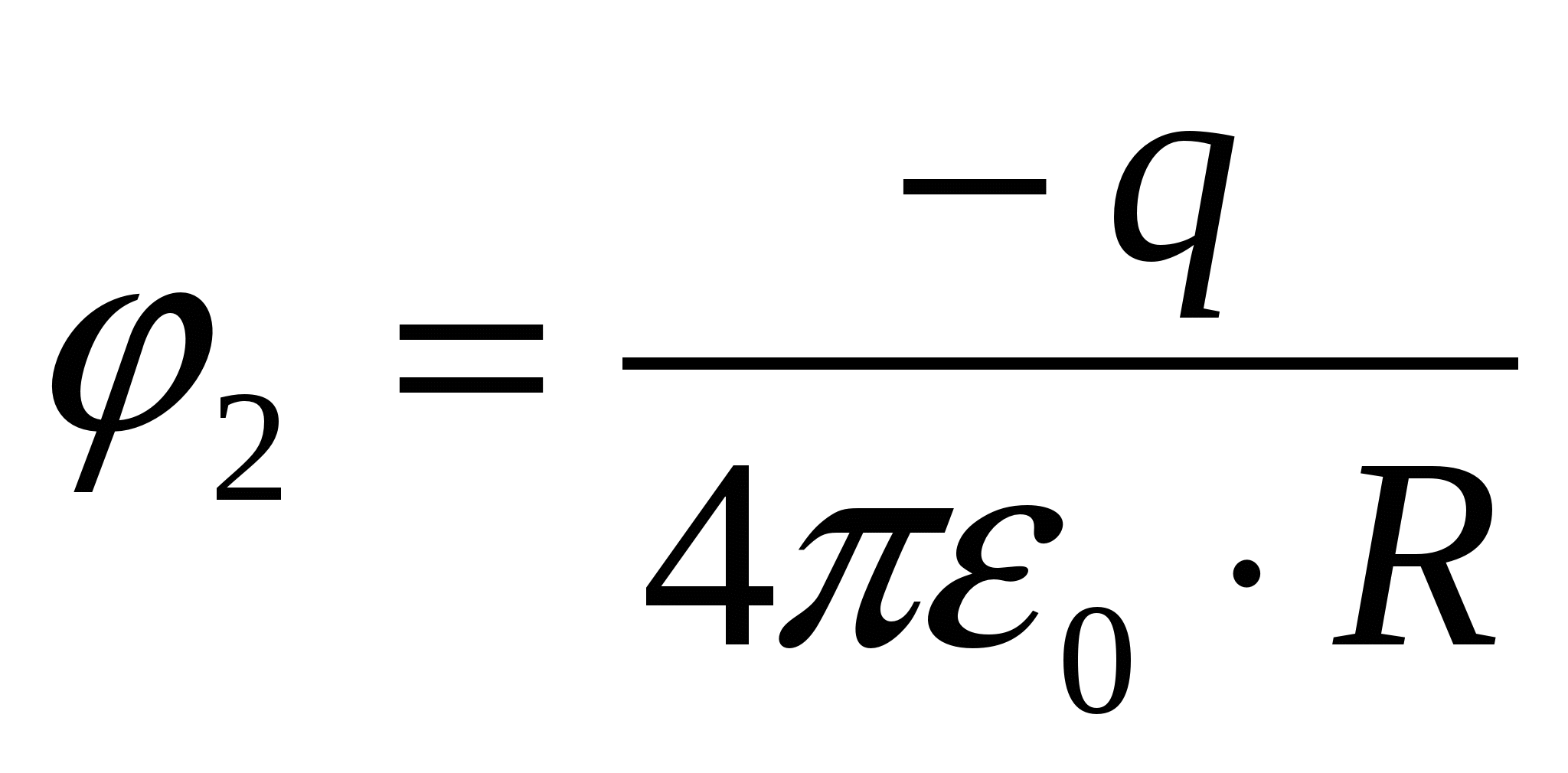 ;
; 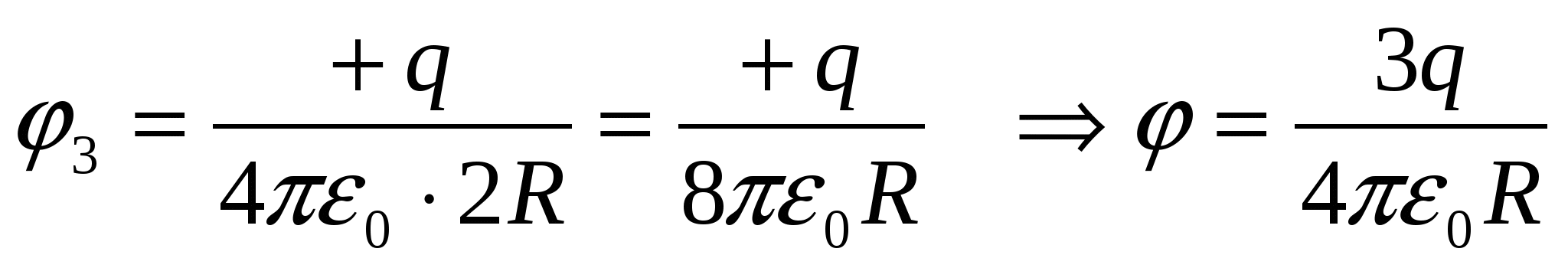 – відповідь 1.
– відповідь 1.
Подібне завдання – А 19 у тесті № 12, 2001 р. :
Всередині кульового металевого шару, внутрішній та зовнішній радіуси якого відповідно дорівнюють. R та 4 R , на відстані R від центру знаходиться точковий позитивний заряд q . Потенціал у центрі сфери дорівнює ….
Відповідь: 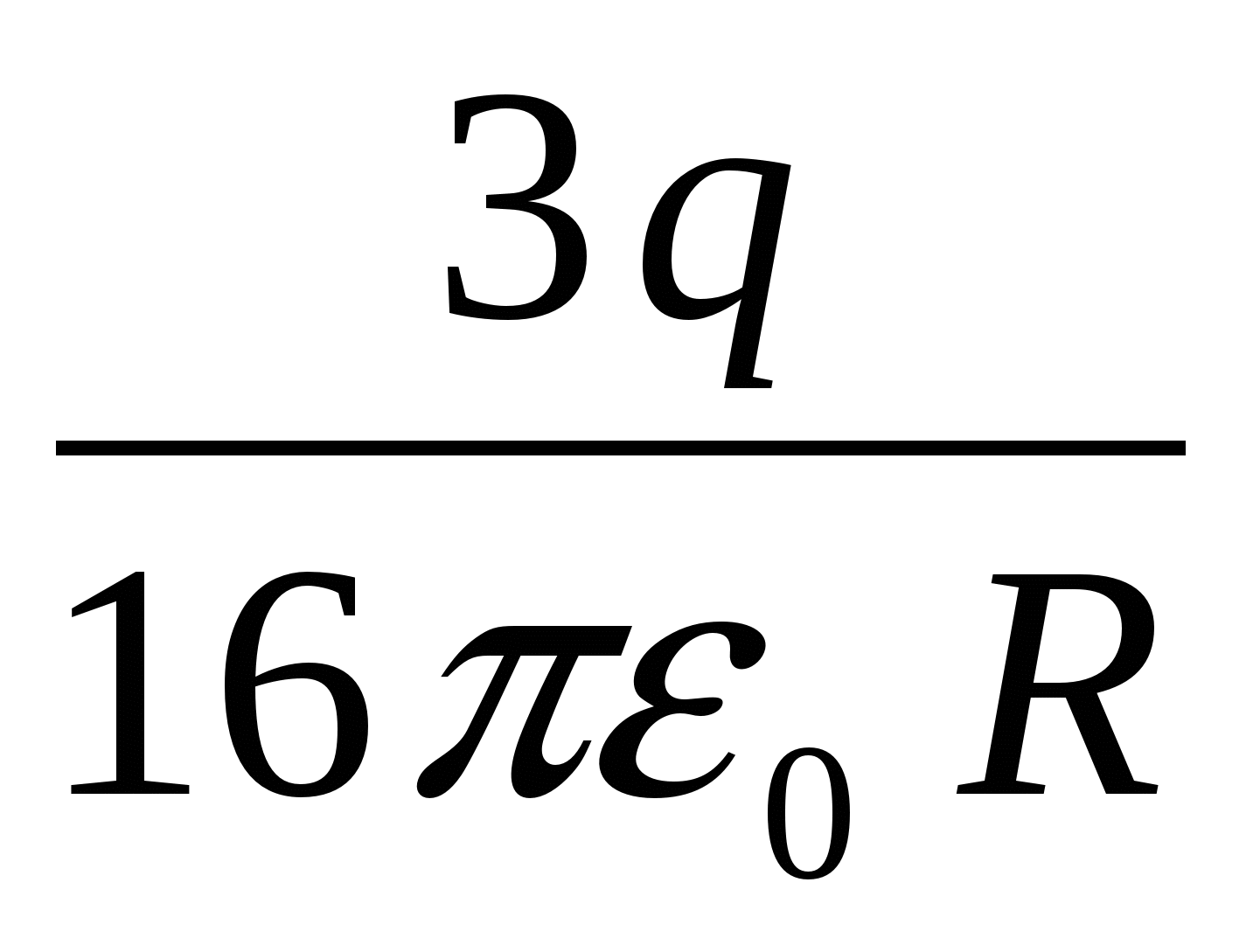
3 (ЦТ 2000 Тест ... А19). Металева куля радіусом R 1 , що має потенціал φ 1 , оточують незарядженою сферичною провідною оболонкою радіусом. R 2 . Знайдіть потенціал кулі після того, як вона буде на деякий час з'єднана з оболонкою?
Рішення
Потенціал зарядженої кулі 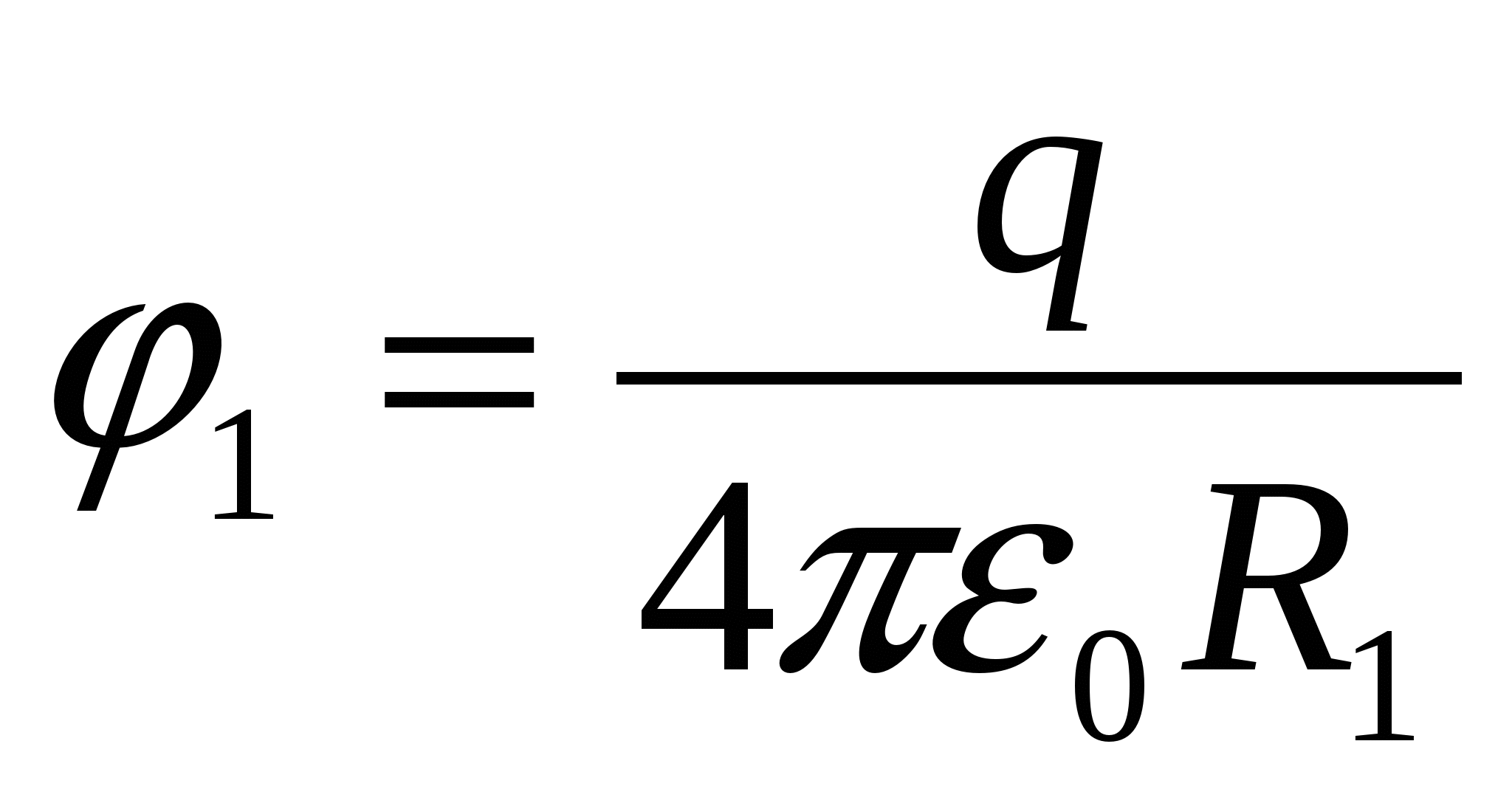 .
.
Якщо заряджений шар стосується внутрішньої поверхні оболонки, заряди, прагнучи розташуватися на можливо великих відстаняходин від одного, переходять на оболонку. Напруженість поля всередині оболонки дорівнює 0, потенціал поля в точках оболонки і всередині неї дорівнює 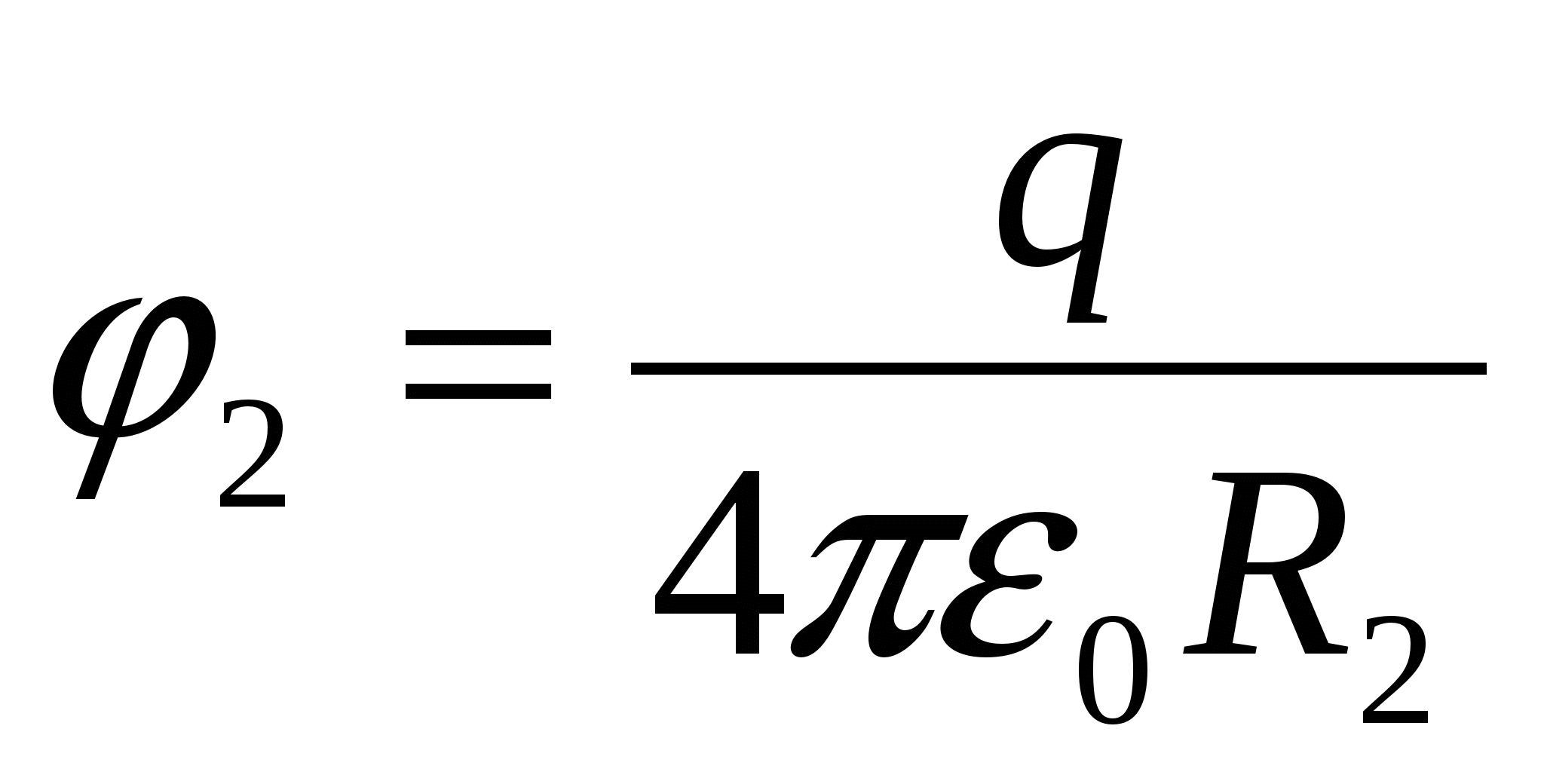 (але не 0!див. попередню задачу), де
(але не 0!див. попередню задачу), де  . Таким чином, потенціал оболонки і кулі, що знаходиться всередині неї і з'єднаної з нею, дорівнює
. Таким чином, потенціал оболонки і кулі, що знаходиться всередині неї і з'єднаної з нею, дорівнює 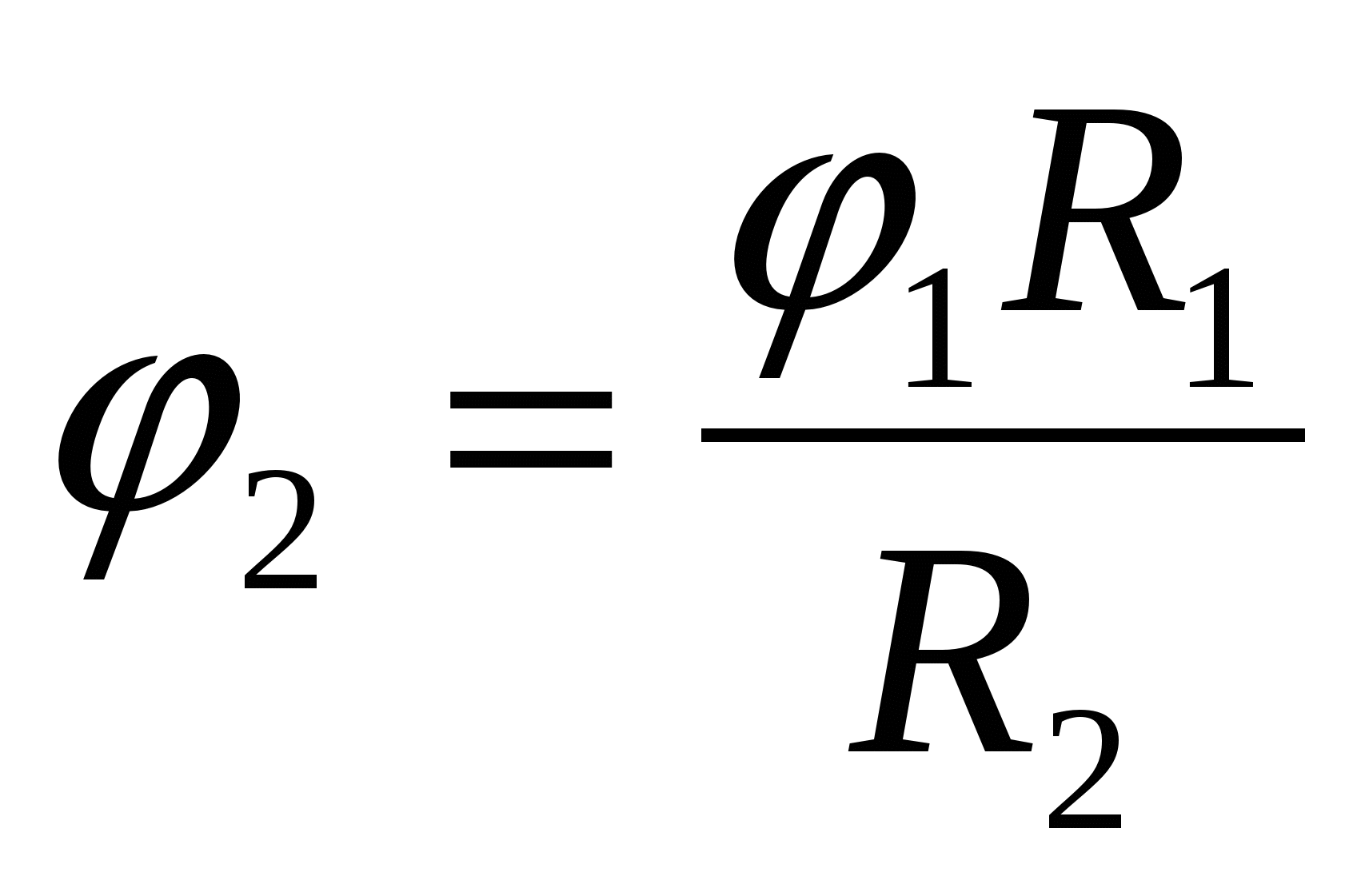 – відповідь.
– відповідь.
Правильний відповідь -1.
4 (ЦТ 2000 Тест ... А19). Металева куля радіусу R 1 , що має потенціал φ 1 , оточують сферичною провідною оболонкою радіусу. R 2 . Чому дорівнюватиме потенціал кулі, якщо заземлити оболонку?
Рішення
Найчастіша помилкаполягає в тому, що не враховується потенціал поля, створеного зарядами, наведеними на оболонці під час її заземлення.
Перший варіант рішення. Потенціал на поверхні кулі, створений зарядом кулі 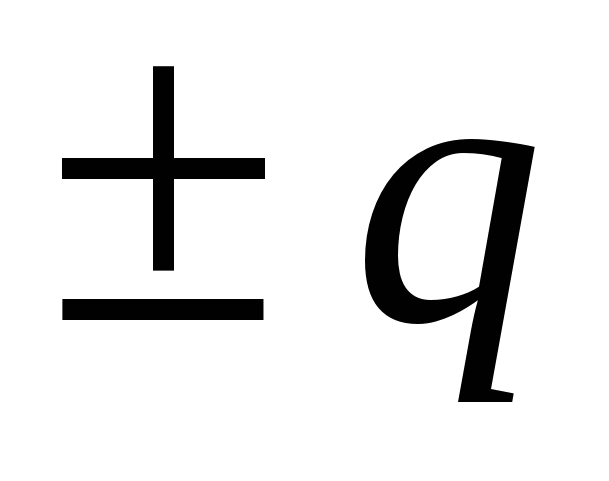 , дорівнює
, дорівнює 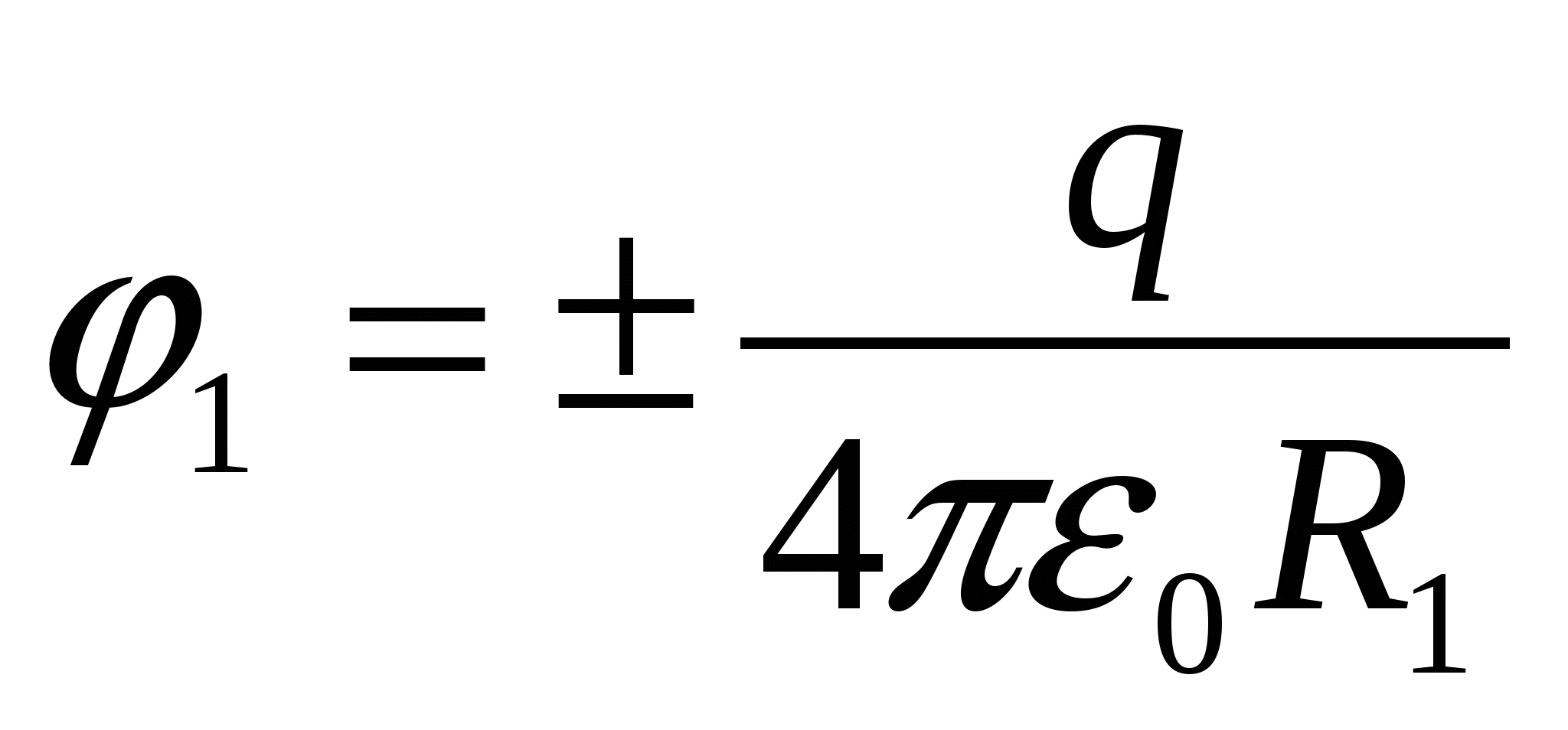 . Після заземлення оболонки на ній утворюється індукований заряд
. Після заземлення оболонки на ній утворюється індукований заряд 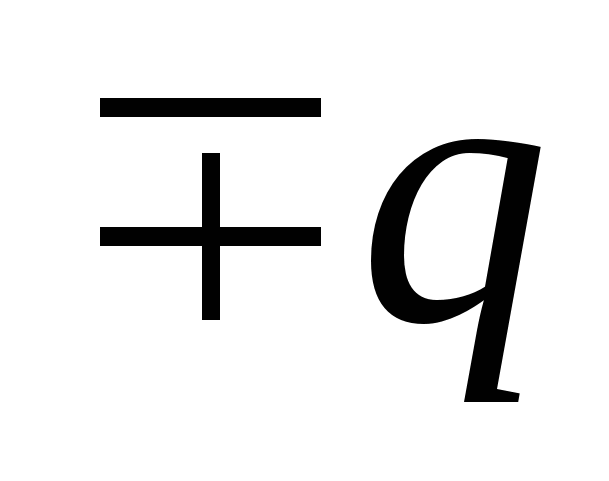 , який на оболонці та всередині неї створює потенціал
, який на оболонці та всередині неї створює потенціал 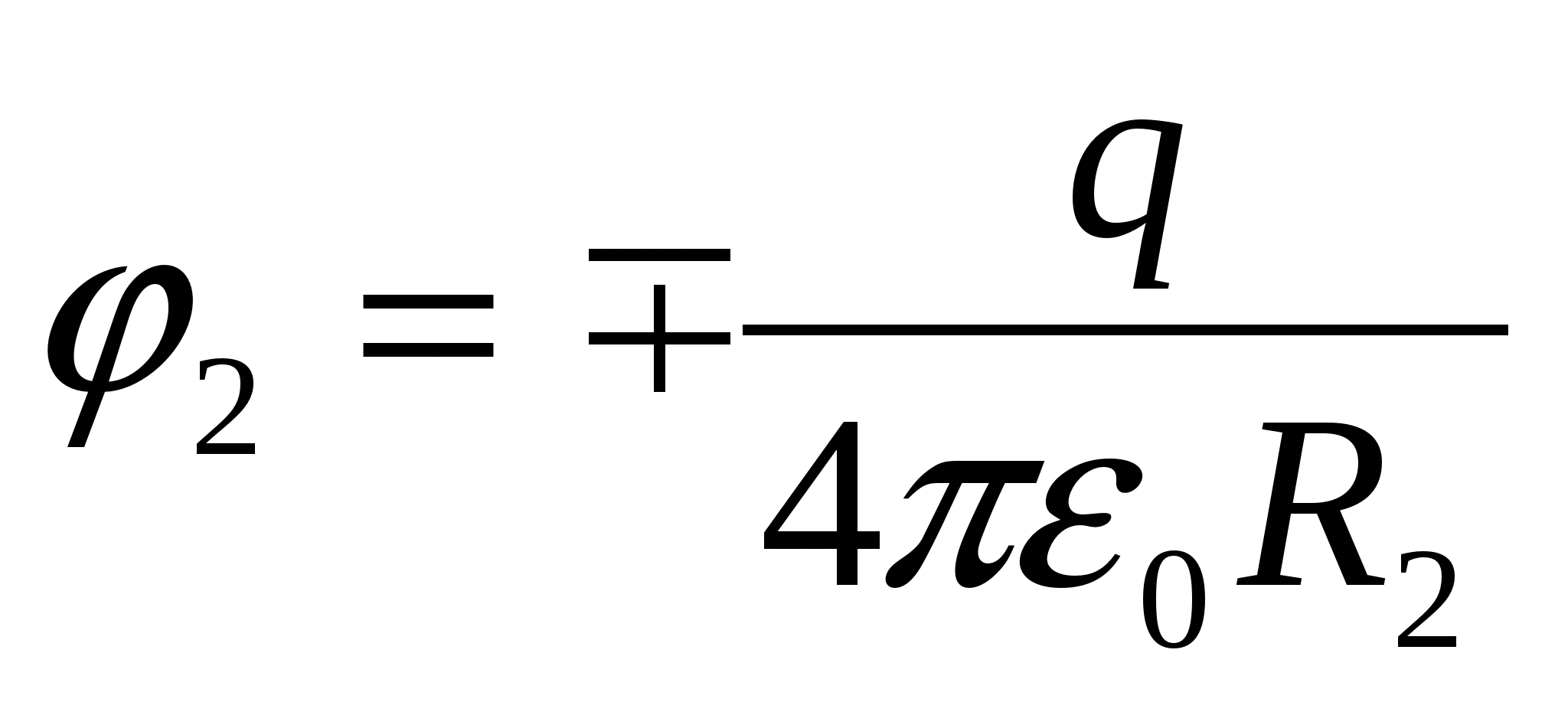 .
.
Суперпозиція вихідного поля кулі та поля, створеного наведеним зарядом оболонки, дає на поверхні кулі потенціал
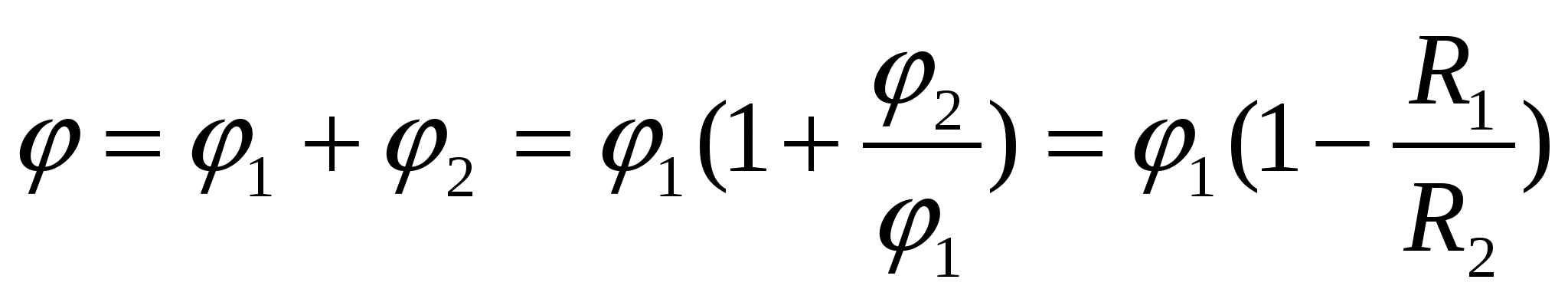 – відповідь.
– відповідь.
Другий варіант рішення. Можна в міркуваннях виходити з того, що потенціал оболонки після заземлення дорівнює 0,як це прийнято в техніці (заземлена оболонка приймається за початок відліку потенційної енергії), з цієї умови знаходиться величина та знак наведеного заряду. Потенціал оболонки φ 2 складається з потенціалу, зумовленого наведеним на ній зарядом q 2 та потенціалом поля кулі φ 1 :
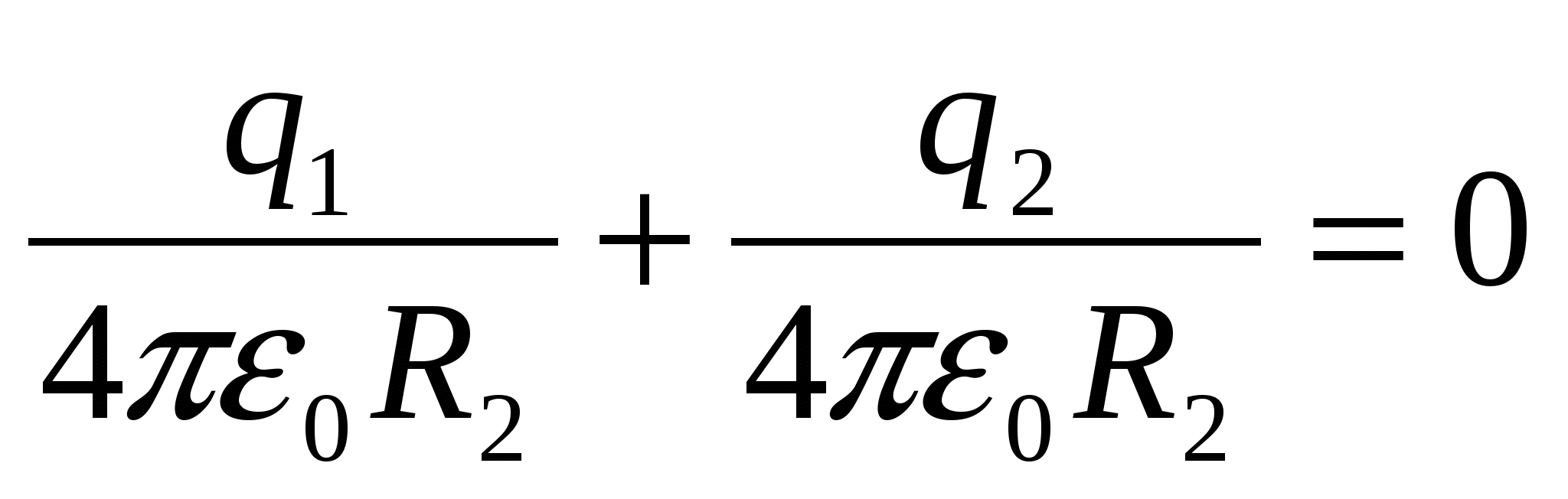 ,
,  q 1
= –
q 2.
.
q 1
= –
q 2.
.
Знаходимо потенціал кулі після заземлення оболонки:
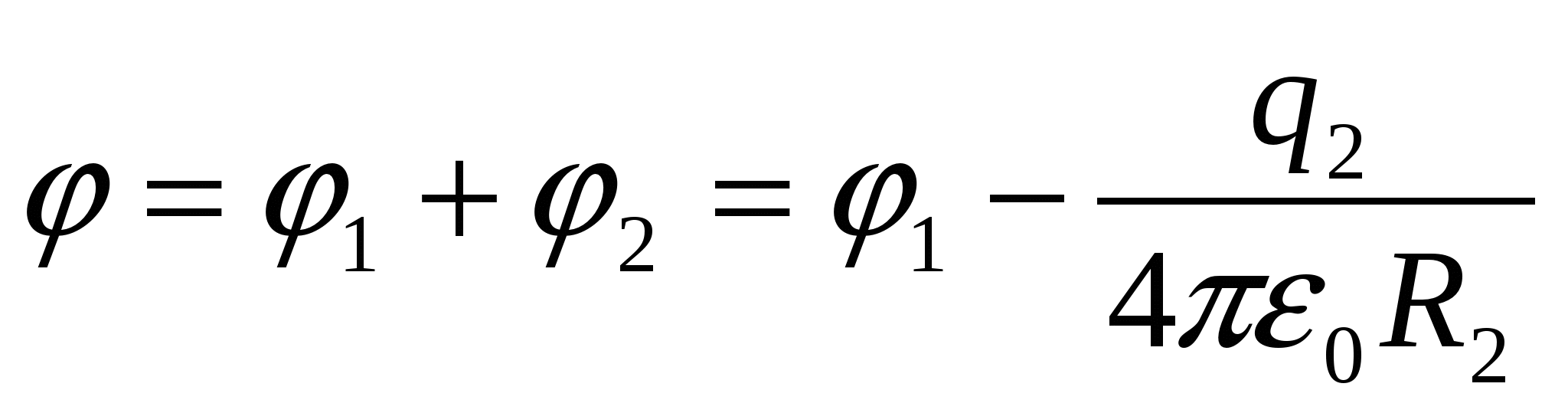 (1).
(1).
З 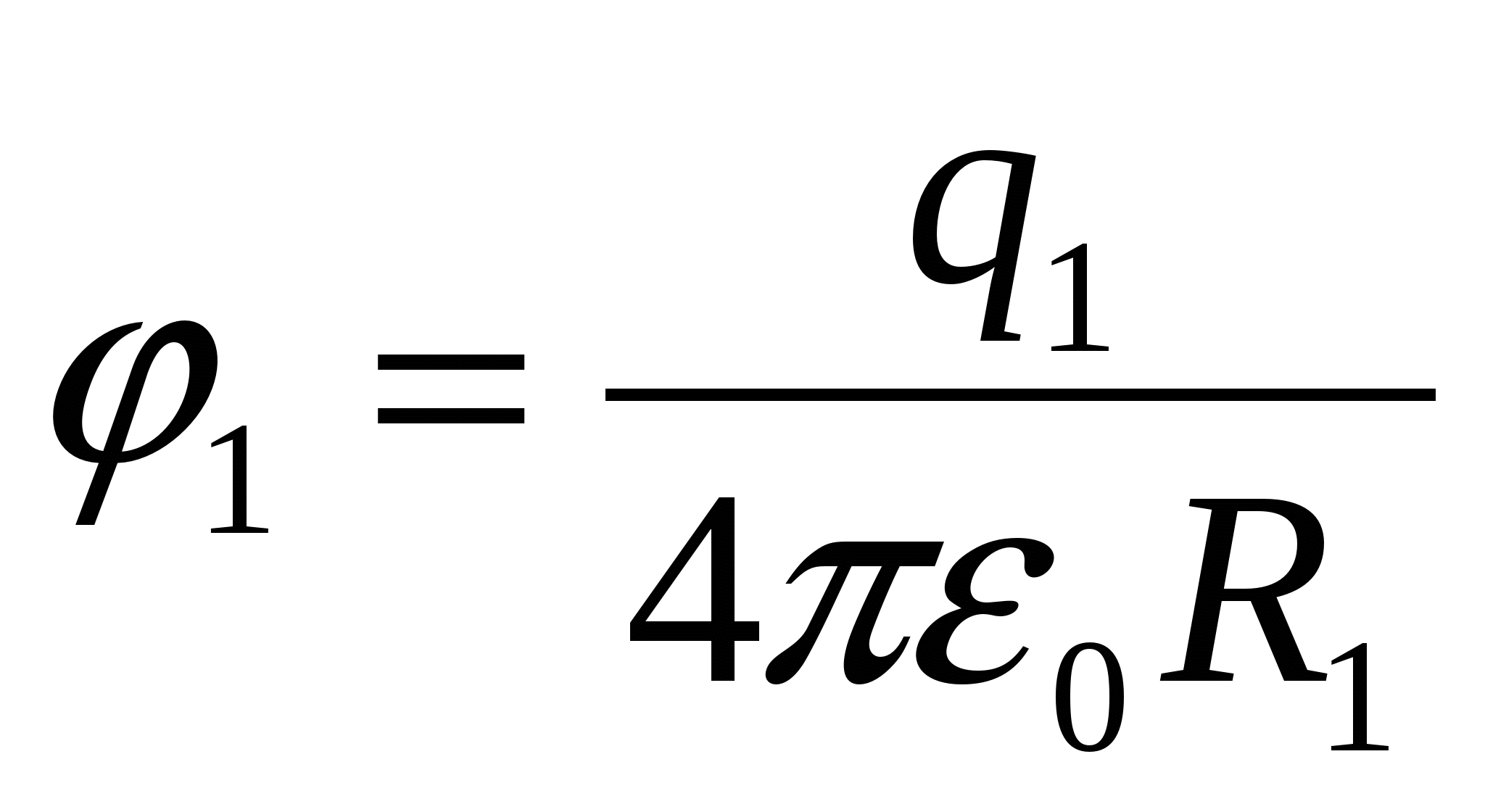 знайдемо
знайдемо 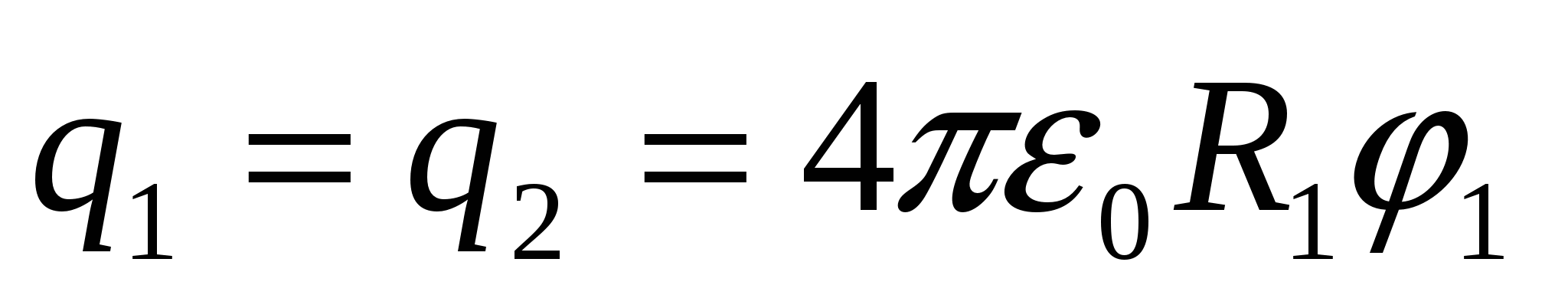 , підставляємо (1), отримуємо відповідь:
, підставляємо (1), отримуємо відповідь: 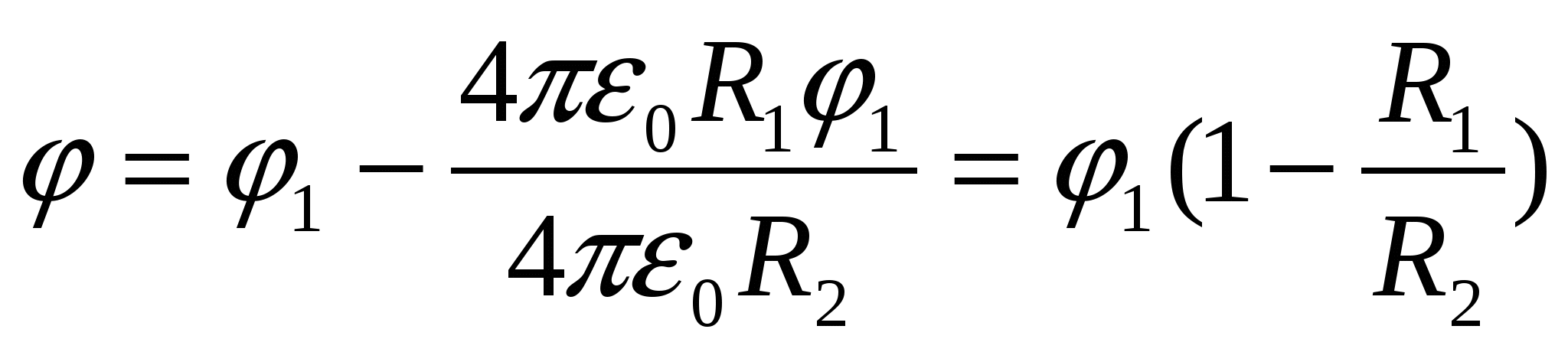 .
.
Цей варіант рішення має мінуси:
- у раніше вирішених завданнях відраховували потенціал (потенційну енергію) від точки, нескінченно віддаленої від заряду, що має ясний фізичний зміст; логічно завжди використовувати один і той же початок відліку;
- Рішення вийшло більш громіздким.
5
(ЦТ 2001 Тест 3. А19). Тонке закріплене кільце радіусу Rрівномірно заряджено так, що на одиницю довжини кільця припадає заряд + γ .
У вакуумі на осі кільця на відстані lвід його центру поміщена маленька кулька, що має заряд + q. Якщо кульку звільнити, то в процесі руху вона придбає максимальну кінетичну енергію, рівну
| 1) 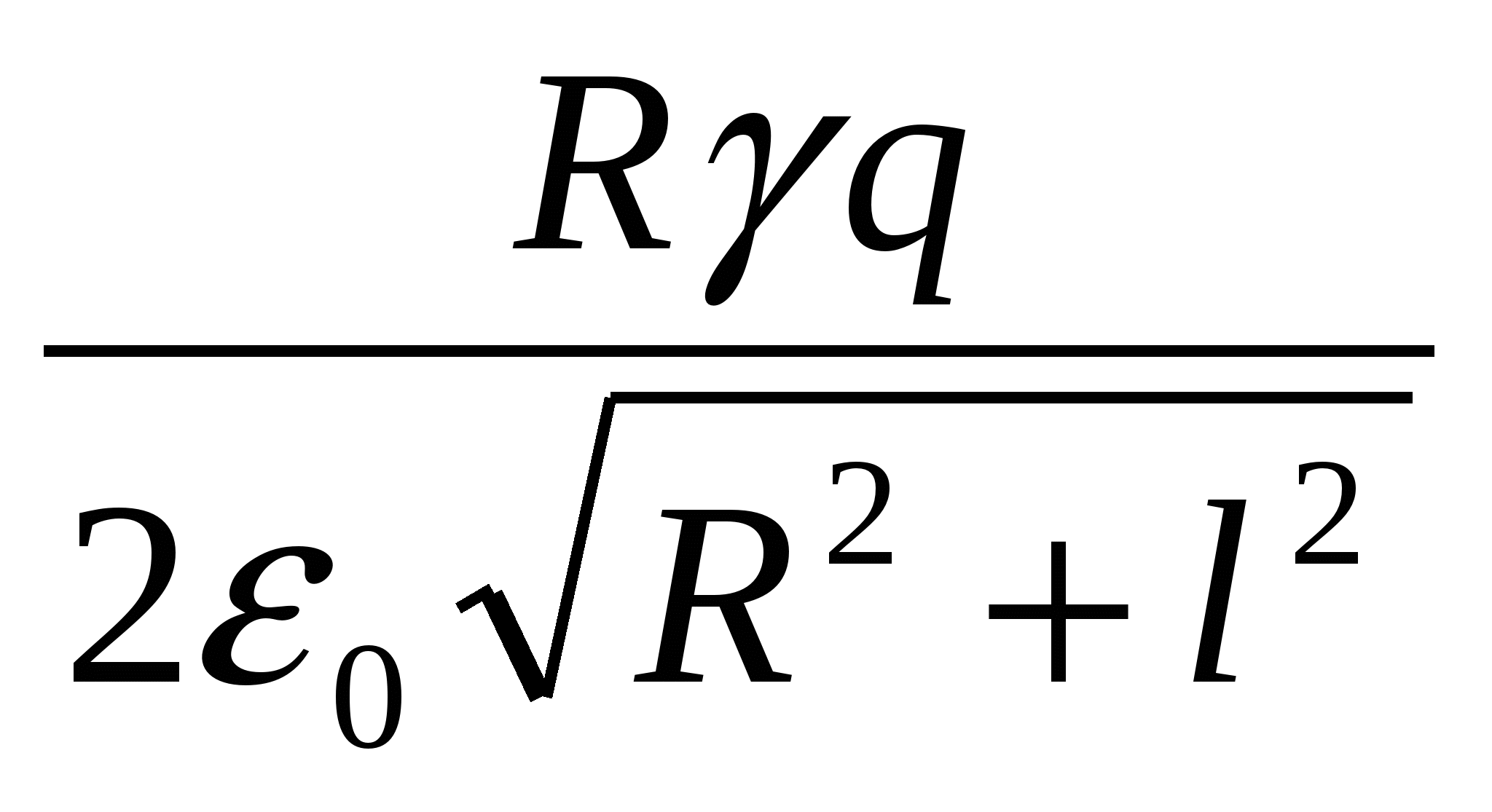 | 2) 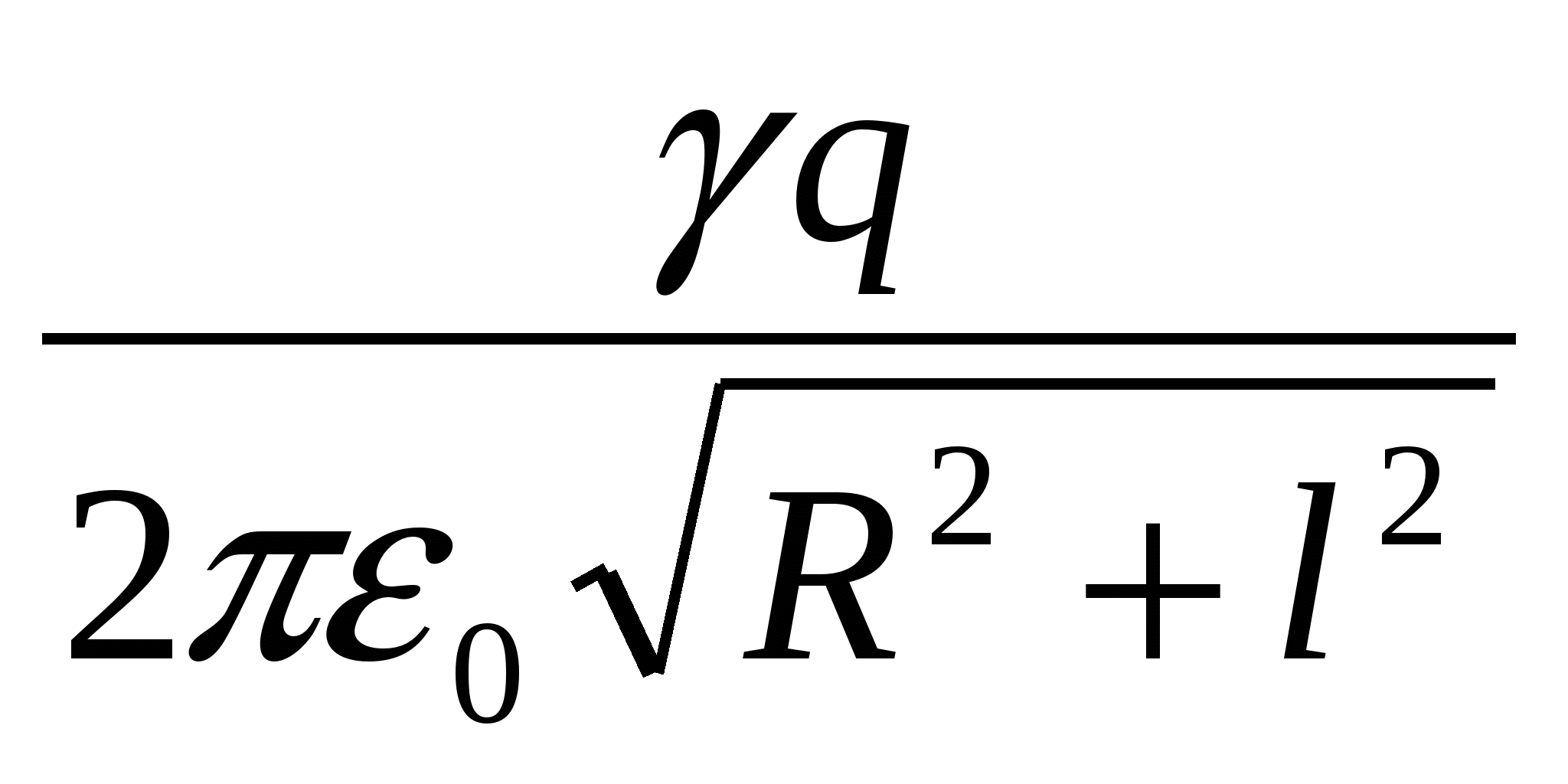 | 3) 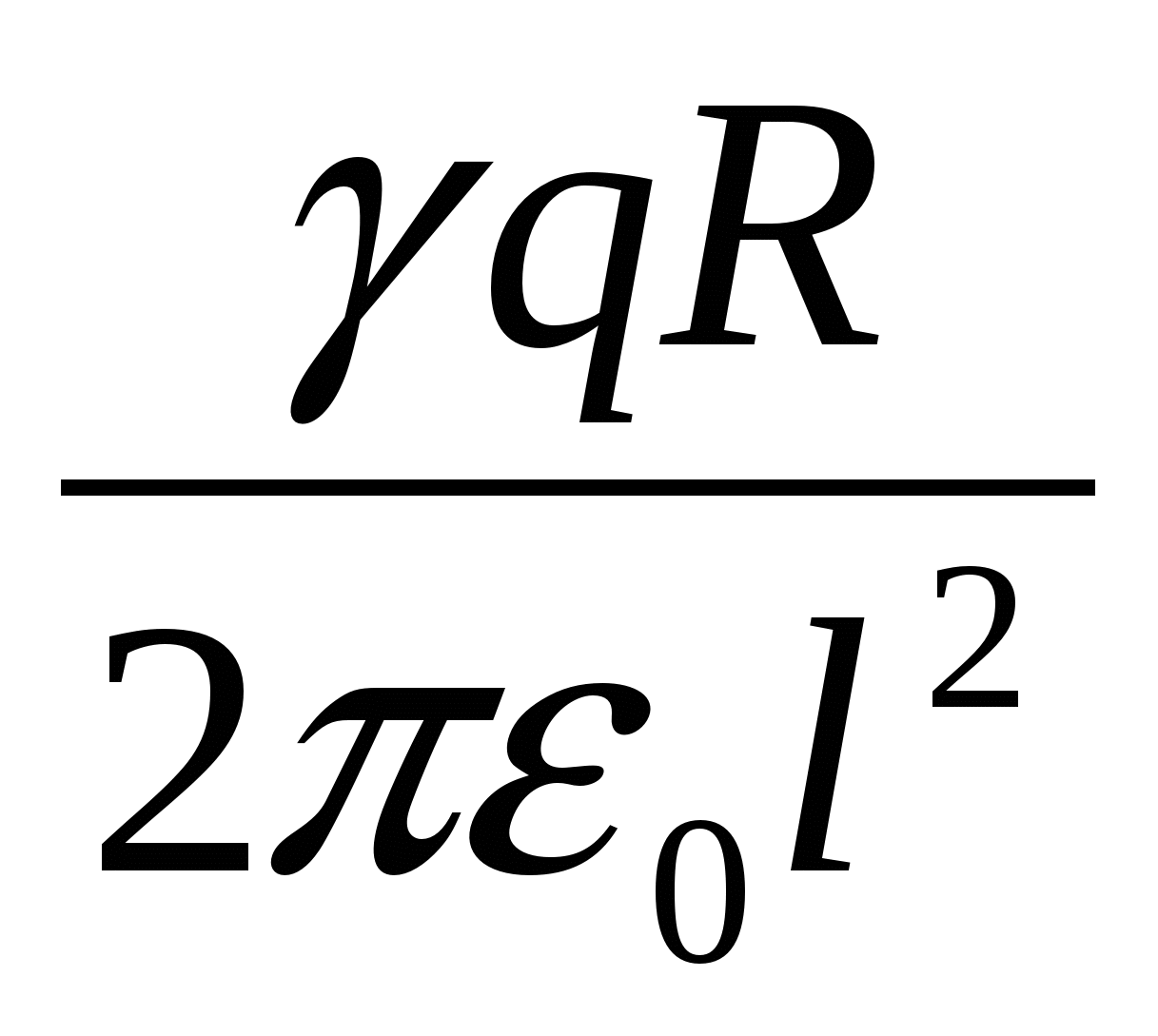 |
| 4) 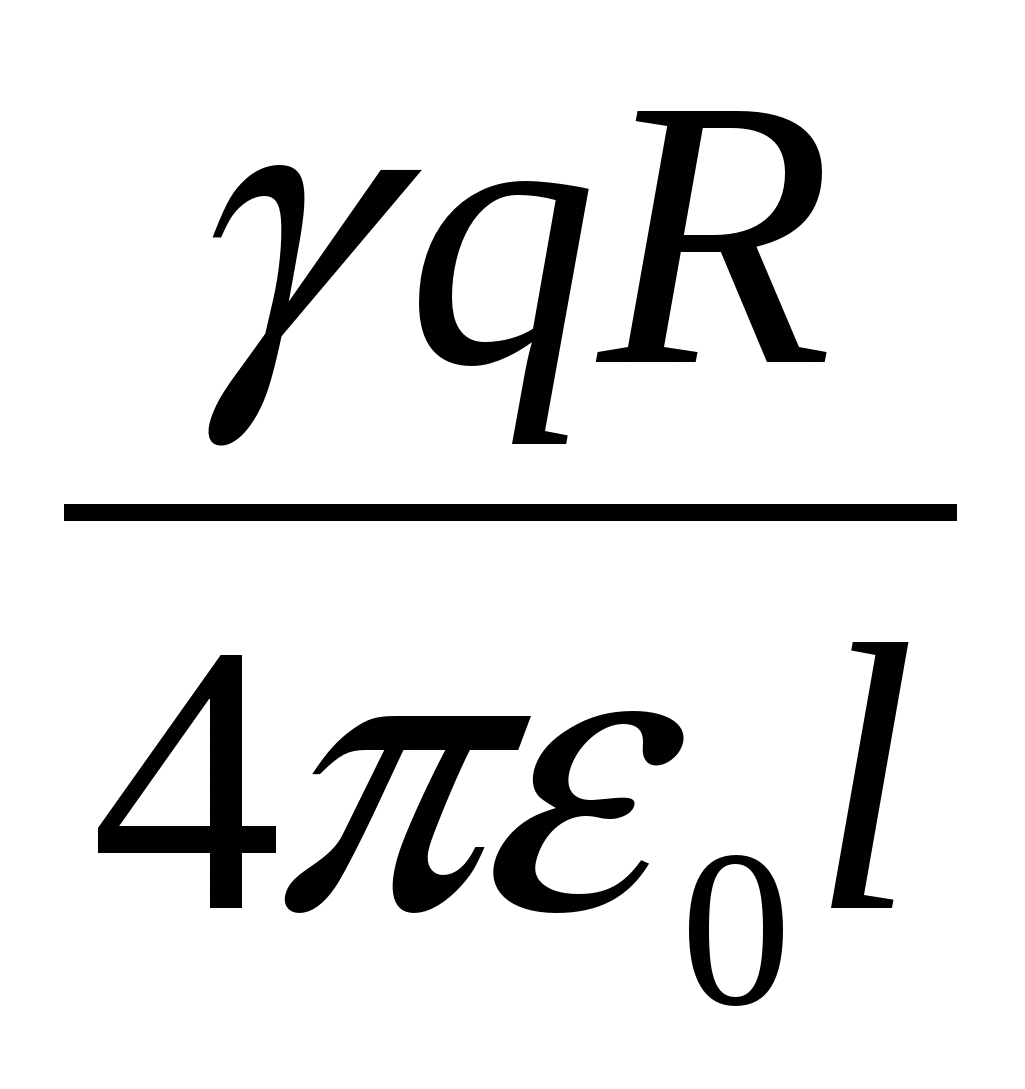 | 5) 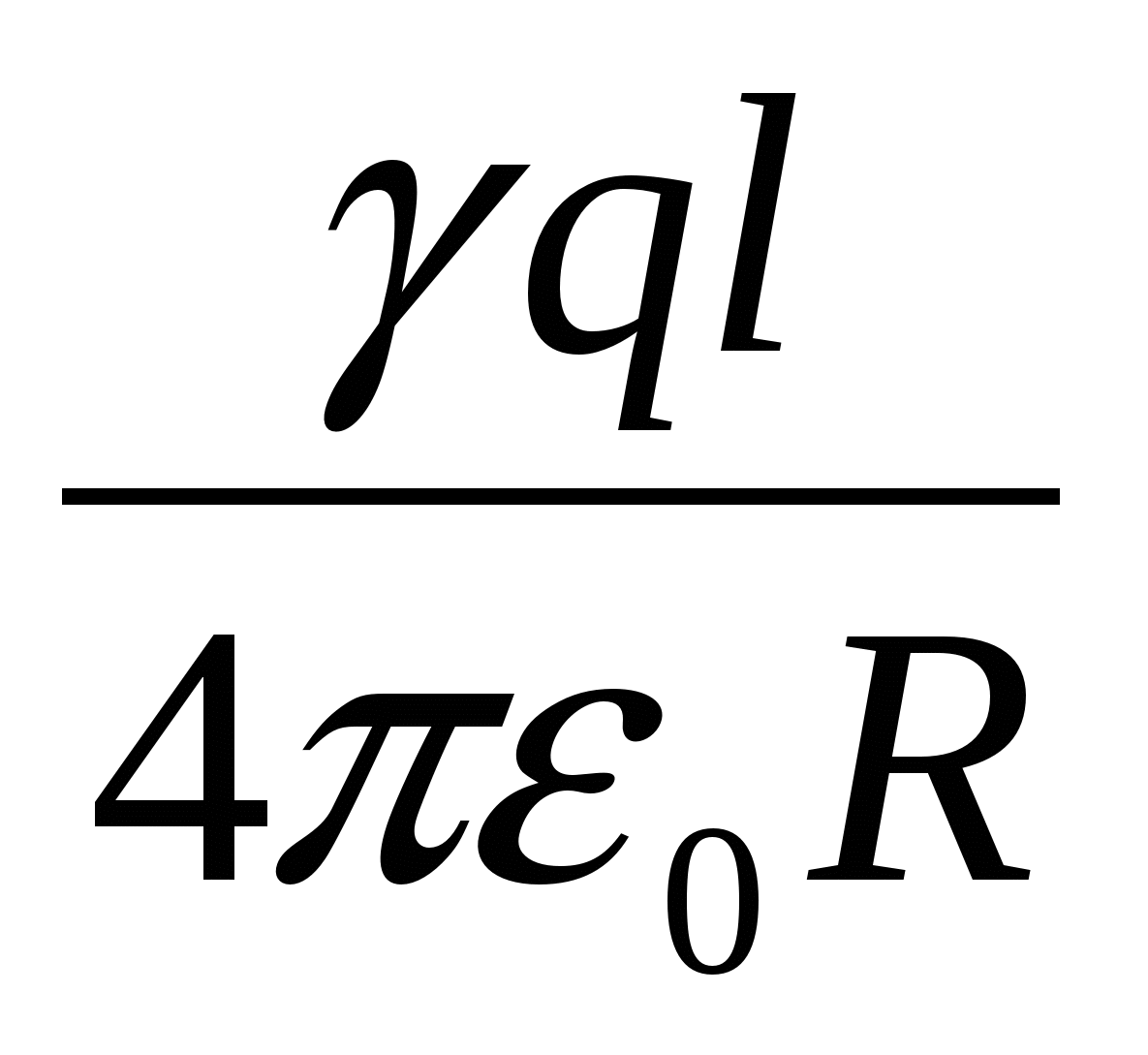 |
Р 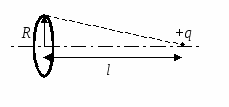 єшення
єшення
За законом збереження енергії E = U, де U- Енергія взаємодії точкового зарядута кільця.
Типова помилка:при вирішенні цього завдання вважають, що через симетричність розподілу заряду по кільцю можна «стягнути» його в центр кільця і знаходити потенціал поля, створеного кільцем у місці знаходження заряду, як потенціал поля точкового заряду: 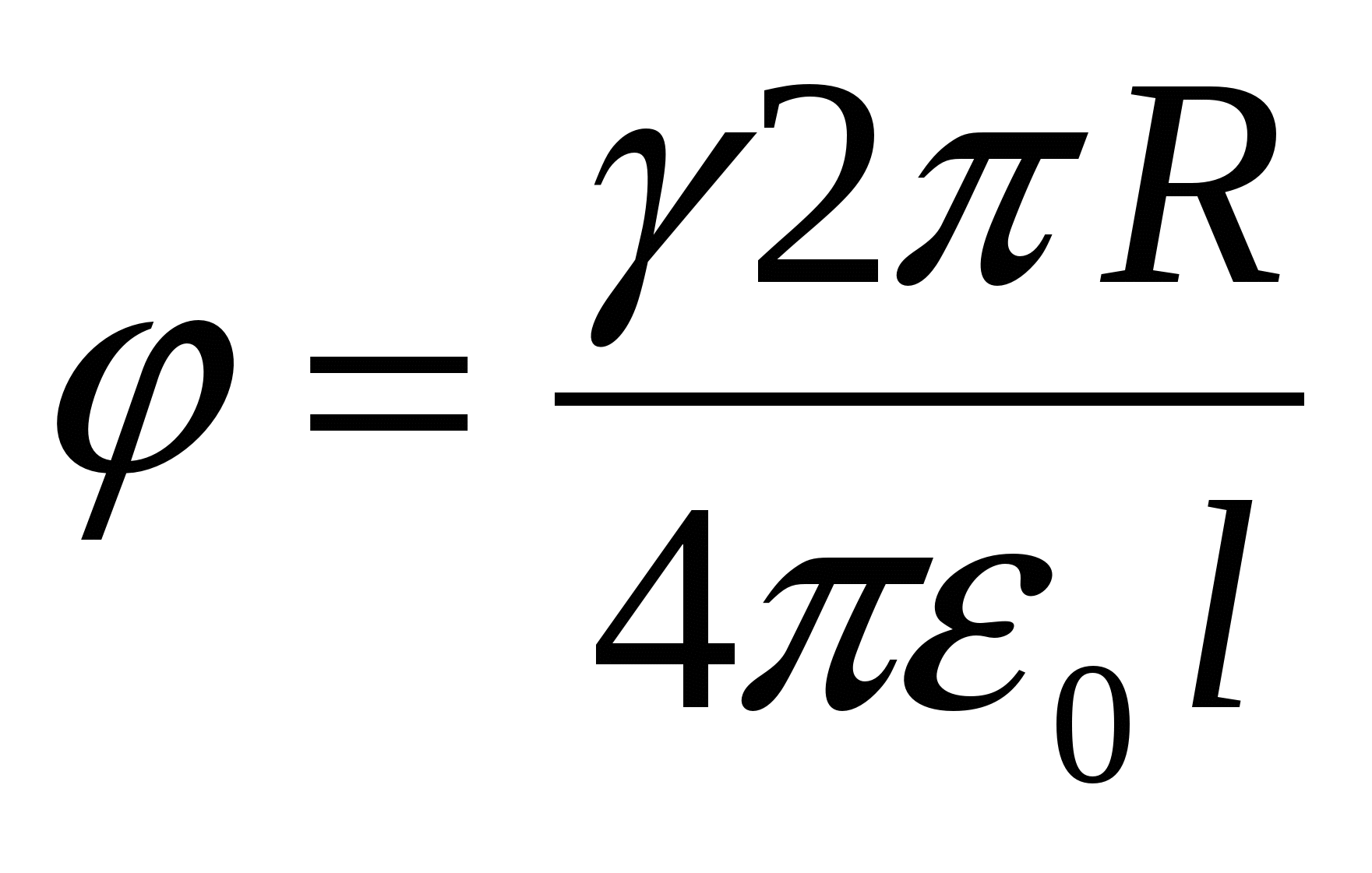 . Однак так чинити не можна, оскільки симетрія заряду не просторова, а площинна. Насправді слід розбити обручку на малі елементи, які можна вважати матеріальними точкамивизначити потенціал поля кожного такого точкового заряду в місці знаходження заряду + q
та підсумувати результати:
. Однак так чинити не можна, оскільки симетрія заряду не просторова, а площинна. Насправді слід розбити обручку на малі елементи, які можна вважати матеріальними точкамивизначити потенціал поля кожного такого точкового заряду в місці знаходження заряду + q
та підсумувати результати:
Енергія взаємодії кільця із зарядом та максимальна кінетична енергія заряду рівні, згідно із законом збереження енергії: 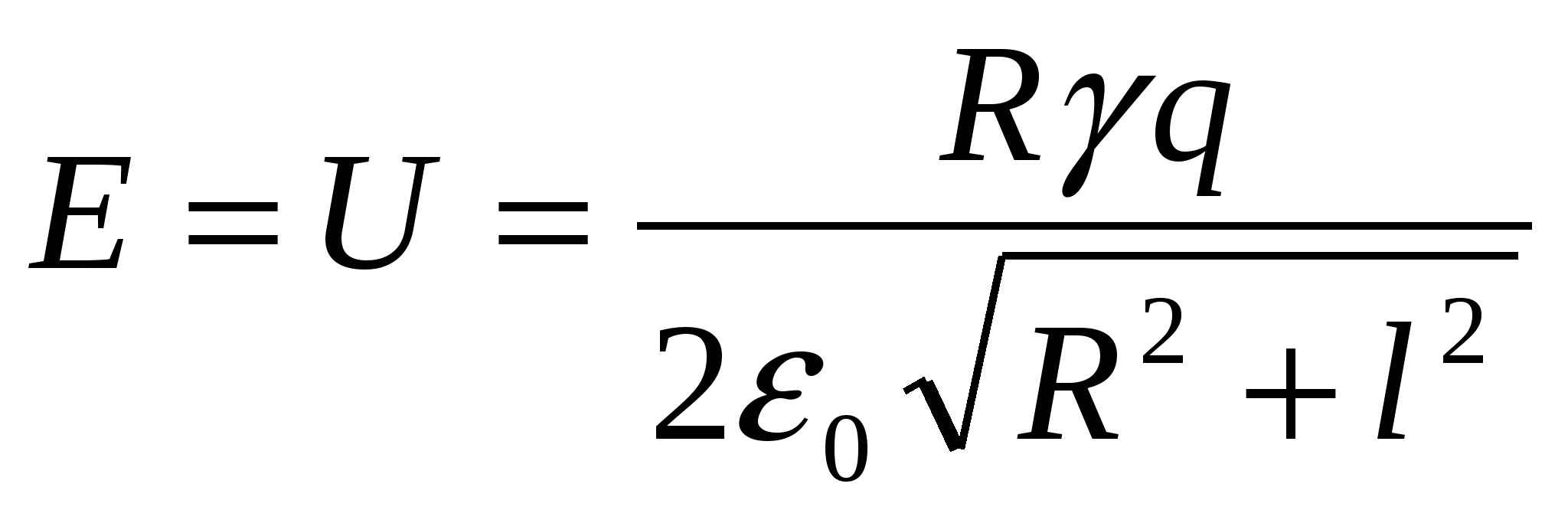 - Відповідь.
- Відповідь.
Подібним чином знаходиться потенціал при розв'язанні задачі А 19 з тесту № 8 ЦТ 2001 р.: по тонкому дротяному кільцю радіуса 3 см рівномірно розподілений заряд 10 -9 Кл. Визначте різницю потенціалів між центром кільця та точкою, що знаходиться на осі кільця на відстані 4 см від центру. Відповідь: 120 Ст.
6
(ЦТ 2000 Тест 3. А 20). Якщо металева куля радіуса R
1
, заряджений до потенціалу φ
1
, з'єднати тонкою
дротом із незарядженою металевою кулею радіусу R
2 то загальний потенціал з'єднання виявиться рівним
| 1) 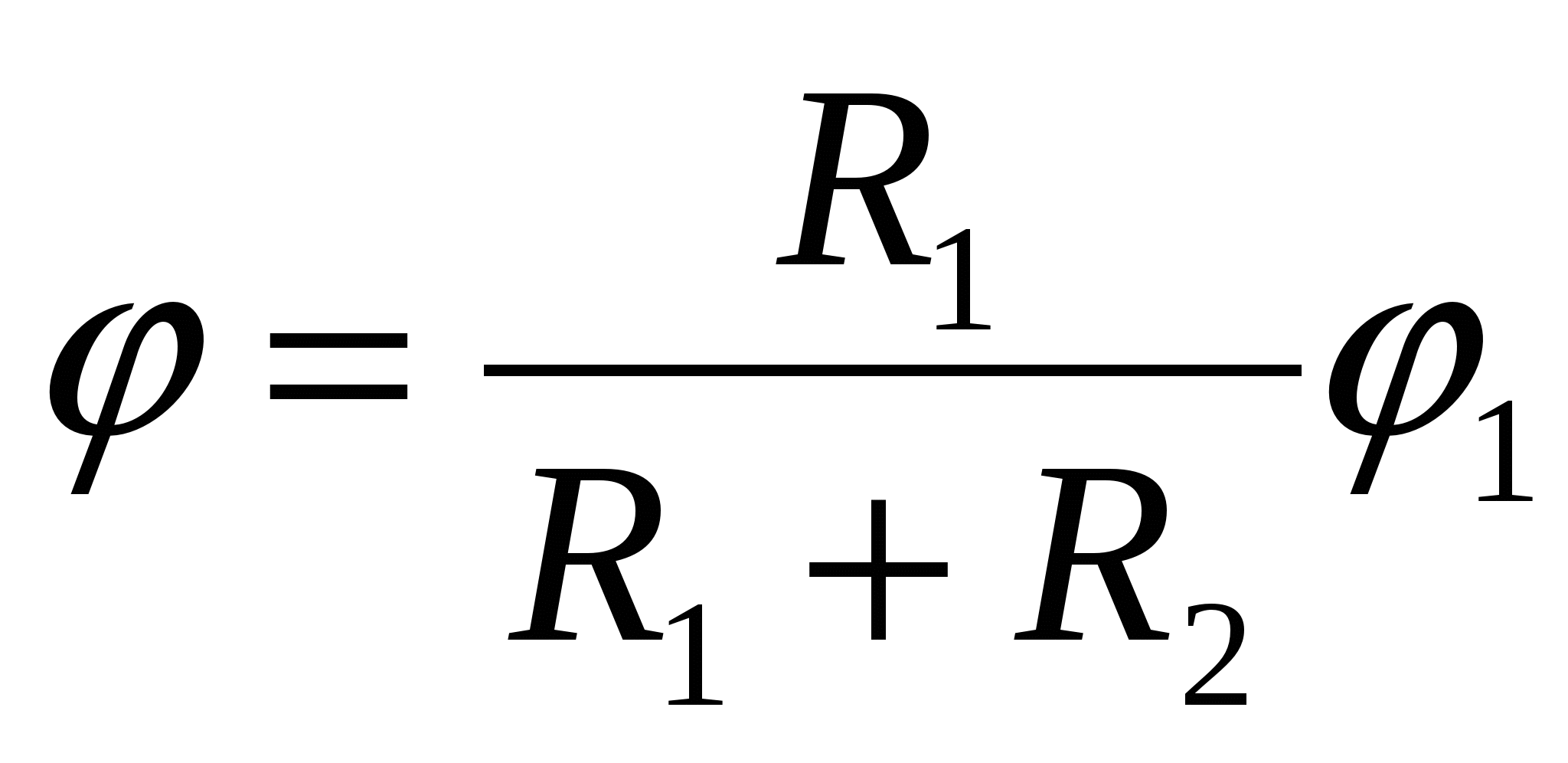 | 2) 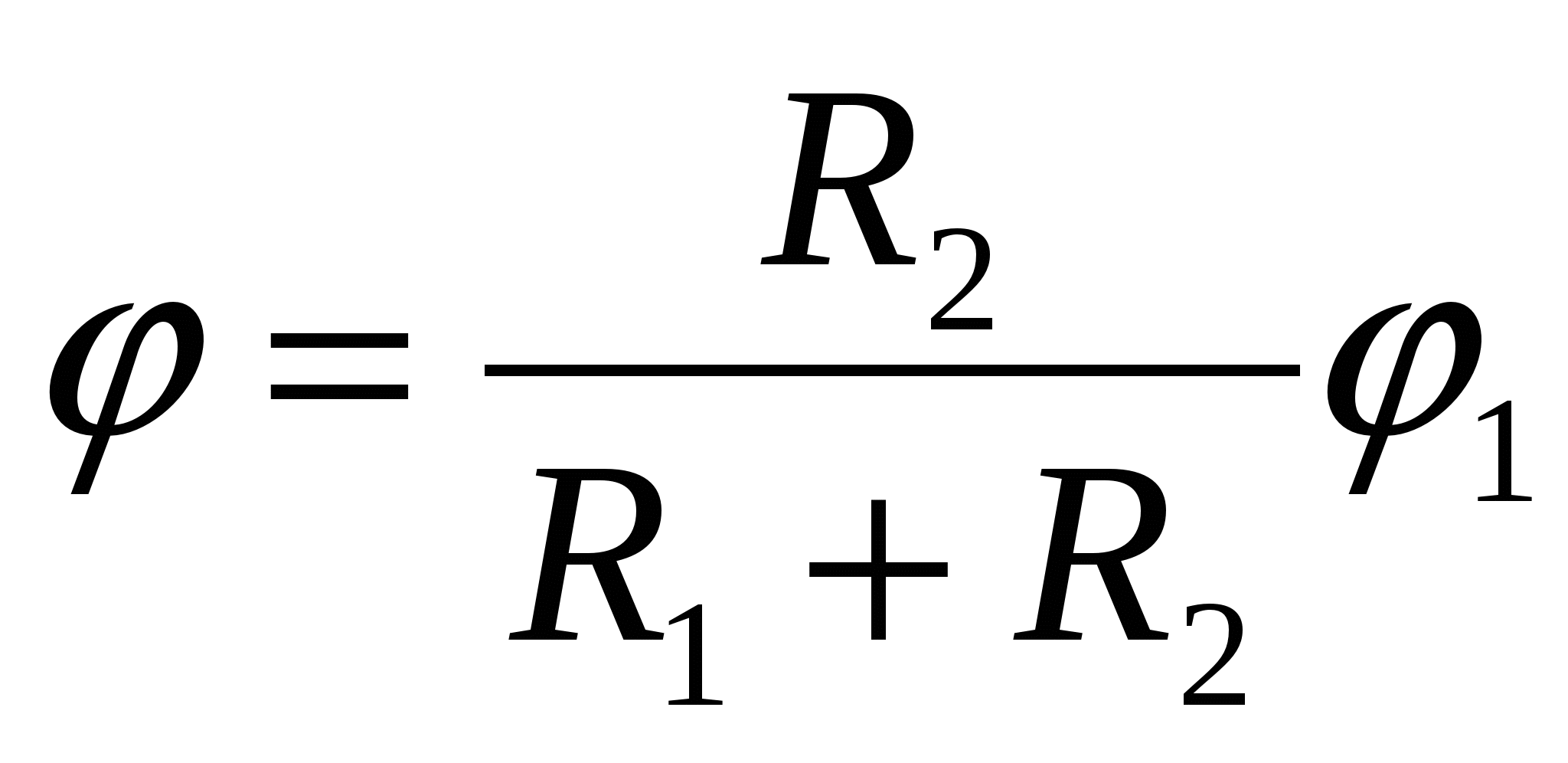 | 3) 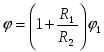 |
| 2) 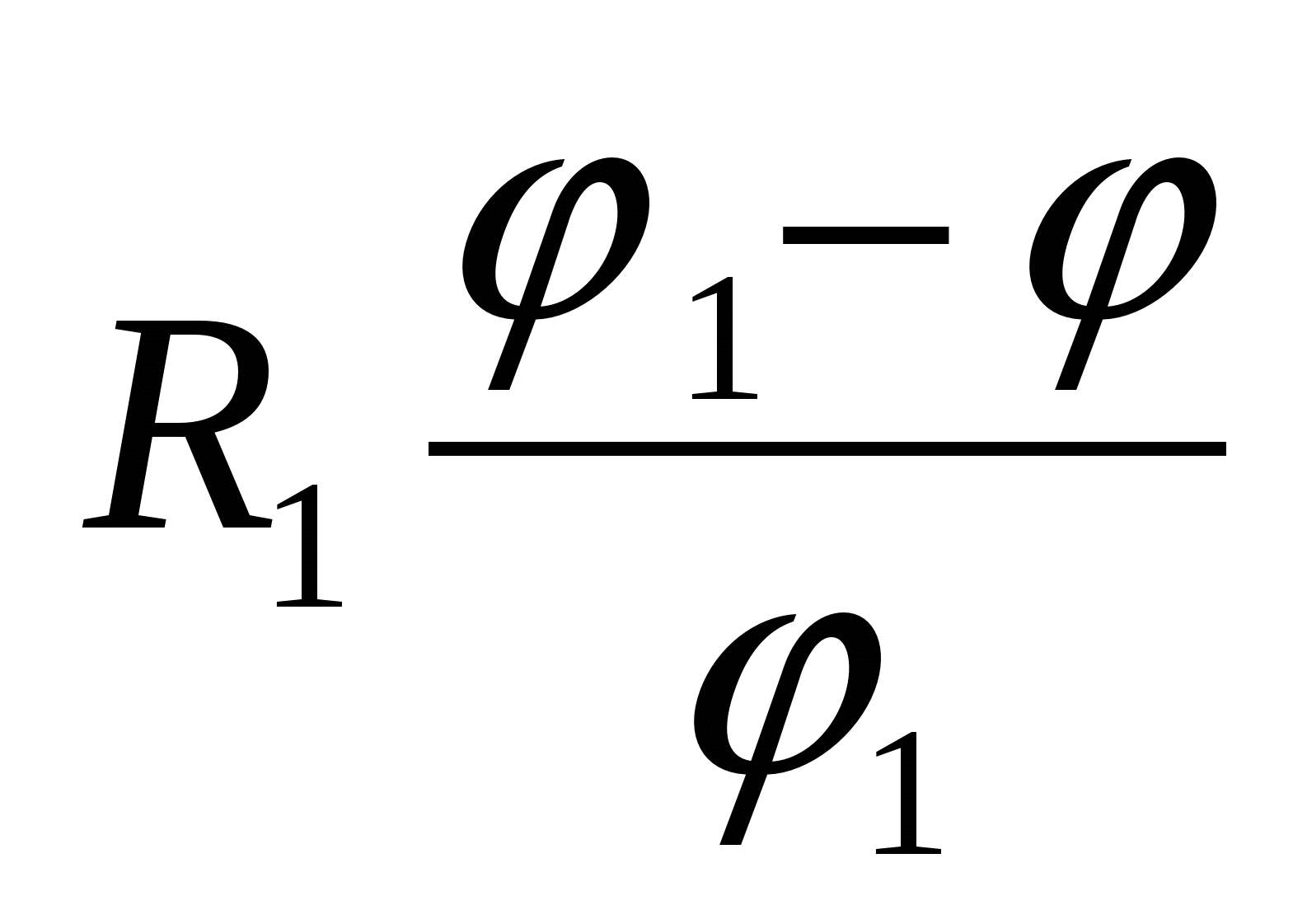 | 3) 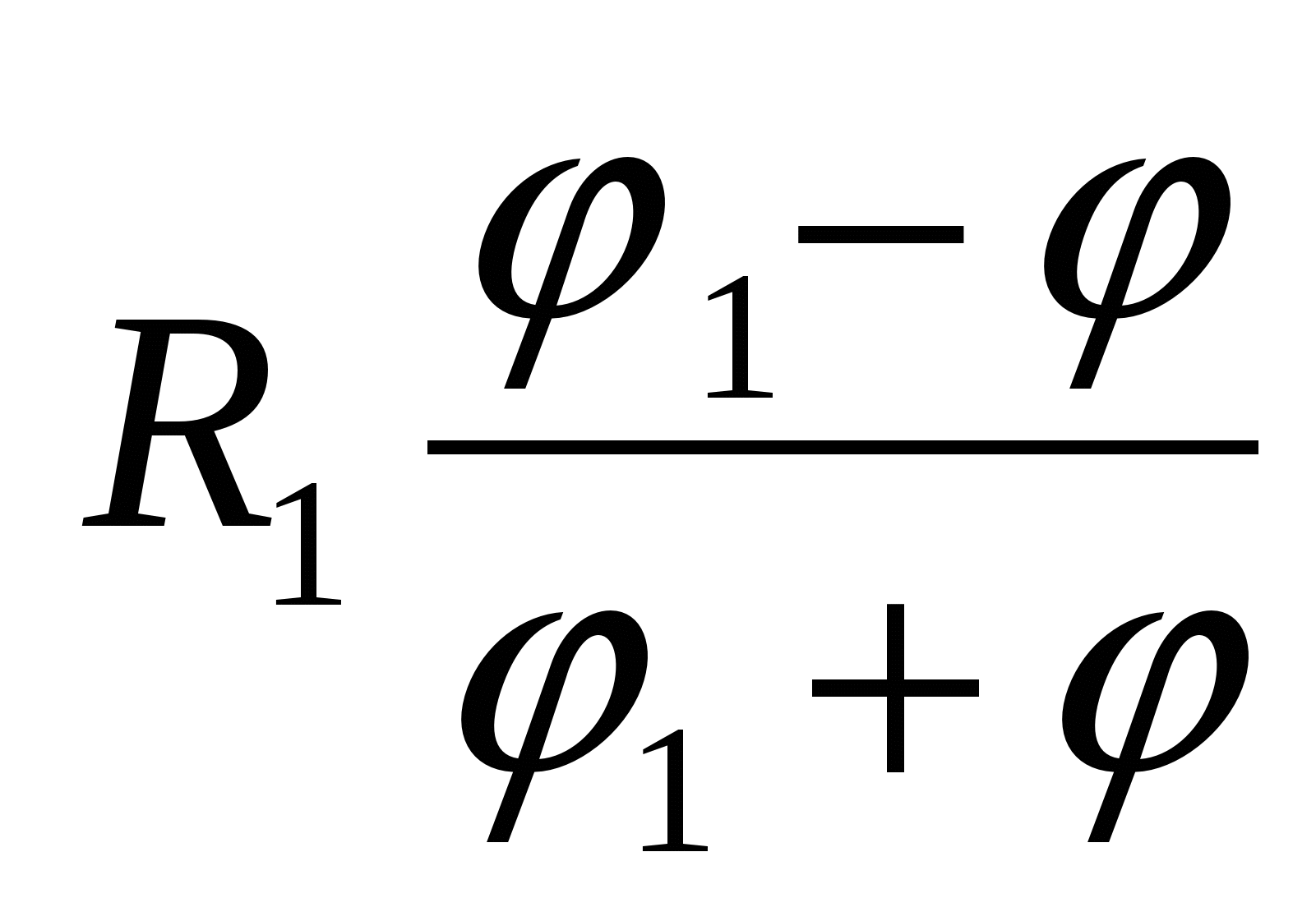 |
|
| 4) 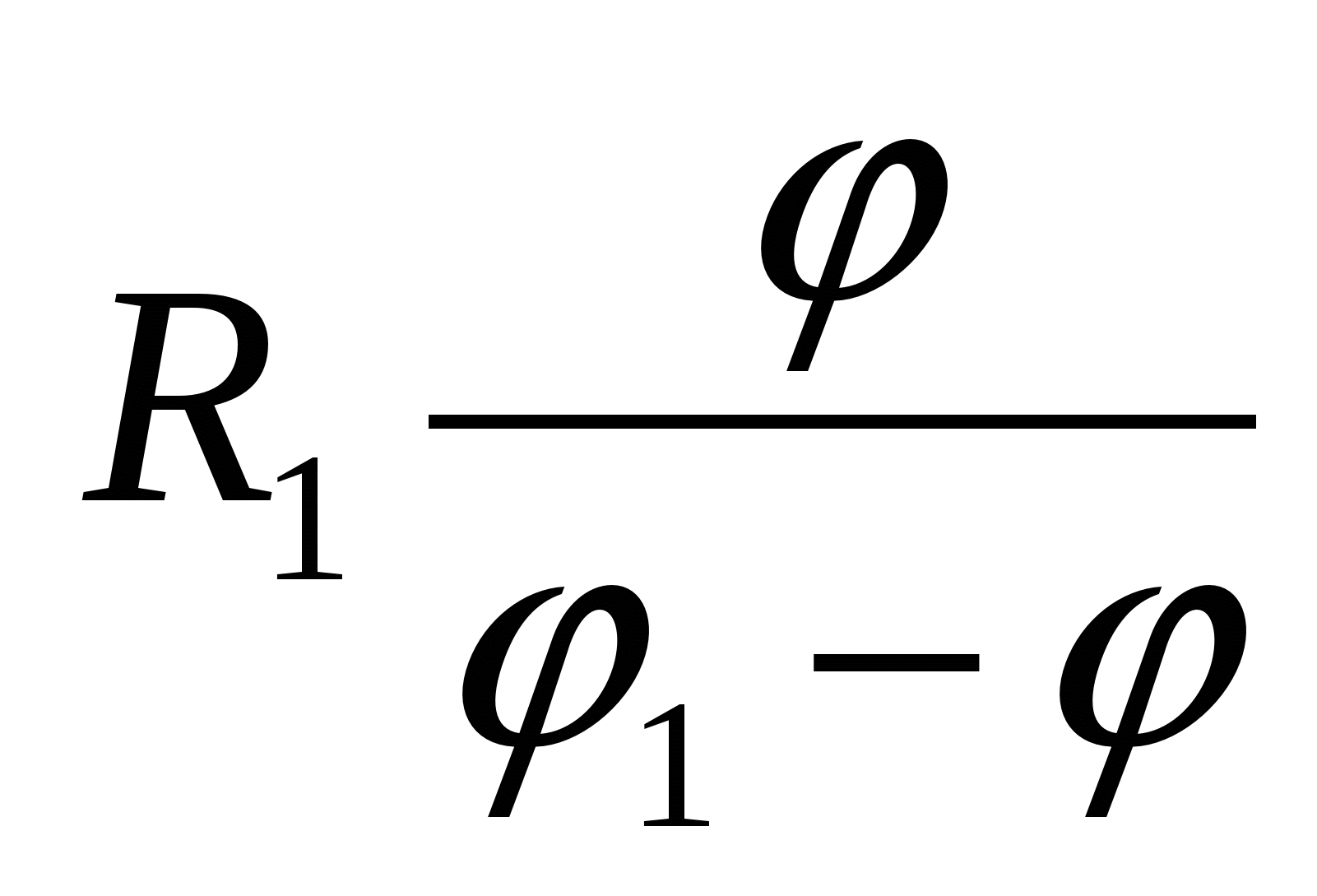 | 5) 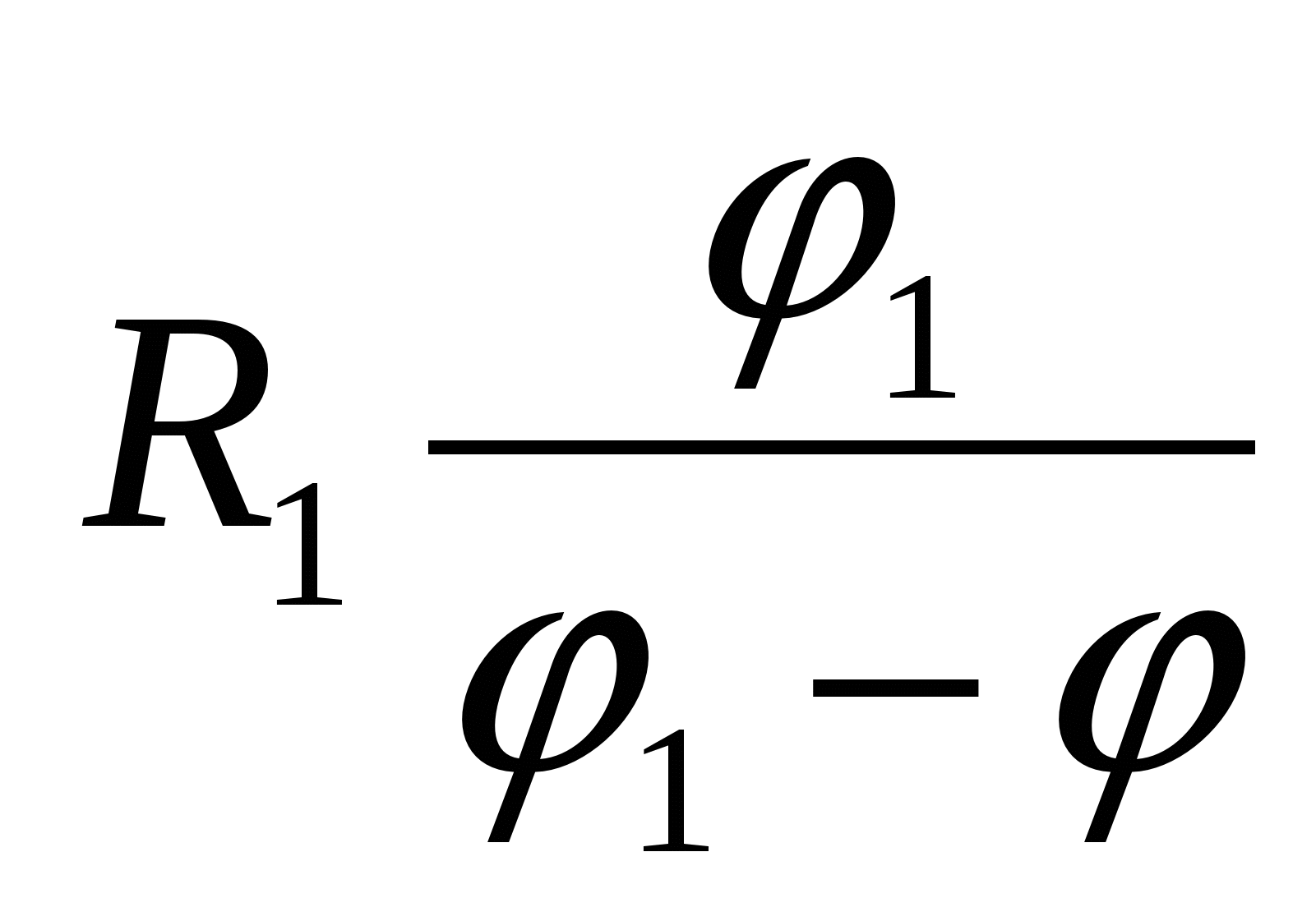 |
7
(ЦТ 2001р. Тест 2. А 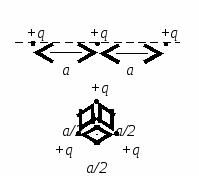 19). Яку роботу треба зробити, щоб три однакові точкові позитивні заряди q, що знаходяться у вакуумі вздовж однієї прямої на відстані a
один від одного, розташувати у вершинах рівностороннього трикутника зі стороною a/2.
19). Яку роботу треба зробити, щоб три однакові точкові позитивні заряди q, що знаходяться у вакуумі вздовж однієї прямої на відстані a
один від одного, розташувати у вершинах рівностороннього трикутника зі стороною a/2.
7.1. Є два електроди у вигляді концентричних сфер з радіусами a(внутрішня) та b(Зовнішня). Така система називається кульовим конденсатором. Знайдіть потенціал будь-якої точки поля між електродами.
7.2. Обчисліть потенціал електричного полядиполя.
7.3. Знайдіть потенціал поля системи зарядів, що знаходяться в обсязі з лінійними розмірами lна відстані.
7.4. Зобразіть потенційну діаграму системи із двох заряджених сфер.
7.5. Обчисліть потенціал поля кулі радіусом a, рівномірно зарядженого за обсягом: а) усередині кулі; б) поза кулею. Зобразіть графік 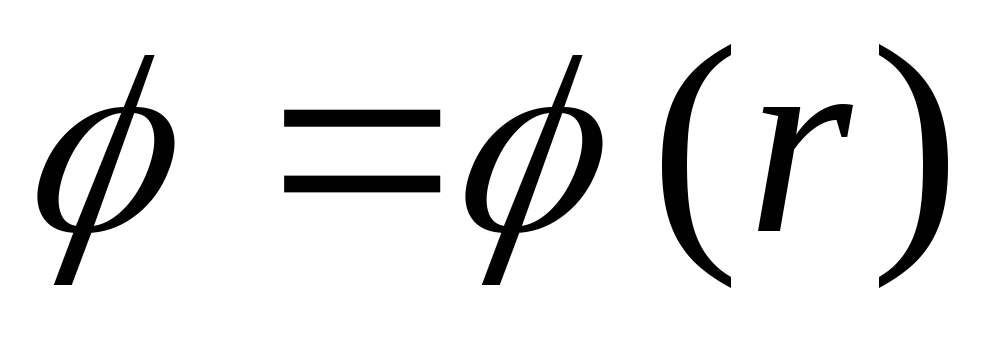 , де - відстань від центру кулі. Розв'яжіть задачу шляхом інтегрування рівняння Пуассона у сферичних координатах, а також використовуючи зв'язок між напруженістю поля та потенціалом.
, де - відстань від центру кулі. Розв'яжіть задачу шляхом інтегрування рівняння Пуассона у сферичних координатах, а також використовуючи зв'язок між напруженістю поля та потенціалом.
7.6. По тонкому дротяному кільцю радіусу Rрівномірно розподілений заряд q. Дослідити залежність потенціалу електричного поля на осі кільця від відстані до центру. Знайти напругу як градієнт потенціалу.
7.7. Сфера радіусу  , рівномірно заряджена зарядом
, рівномірно заряджена зарядом 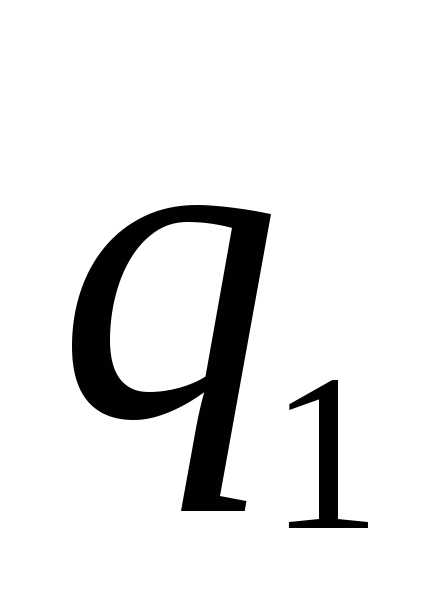 , оточена тонкою концентричною сферою радіусу
, оточена тонкою концентричною сферою радіусу 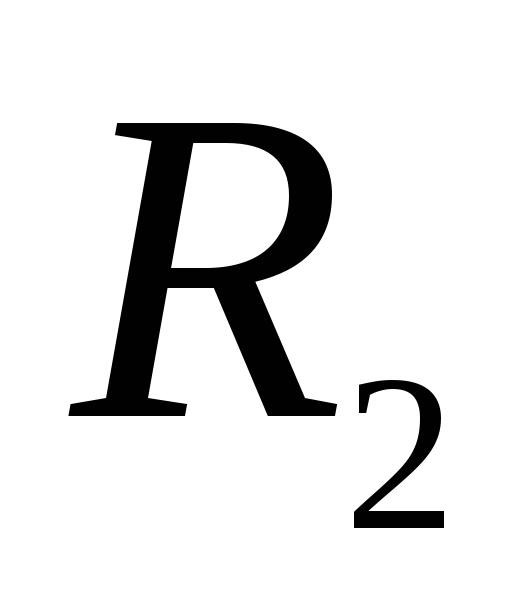 . Який заряд
. Який заряд 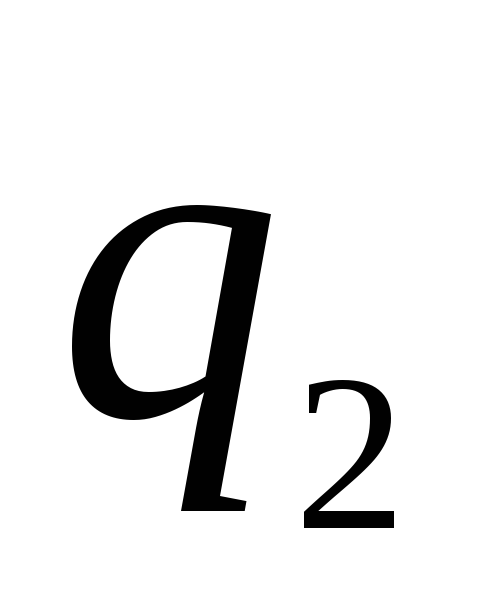 треба повідомити зовнішню сферу, щоб потенціал внутрішньої сфери щодо нескінченності звернувся в нуль? Заряд
треба повідомити зовнішню сферу, щоб потенціал внутрішньої сфери щодо нескінченності звернувся в нуль? Заряд 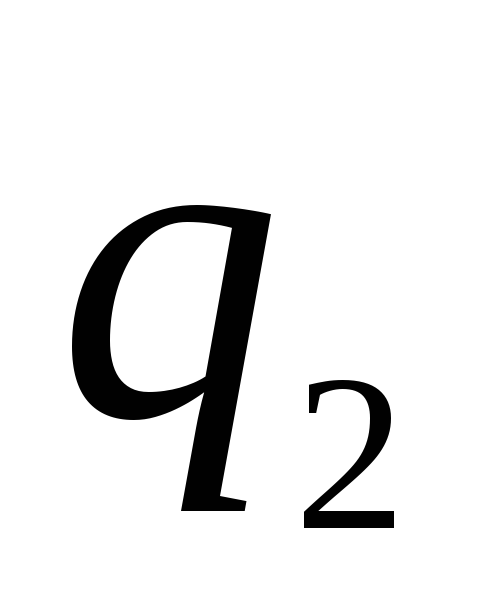 також рівномірно розподілено на його поверхні.
також рівномірно розподілено на його поверхні.
Розв'язання задач
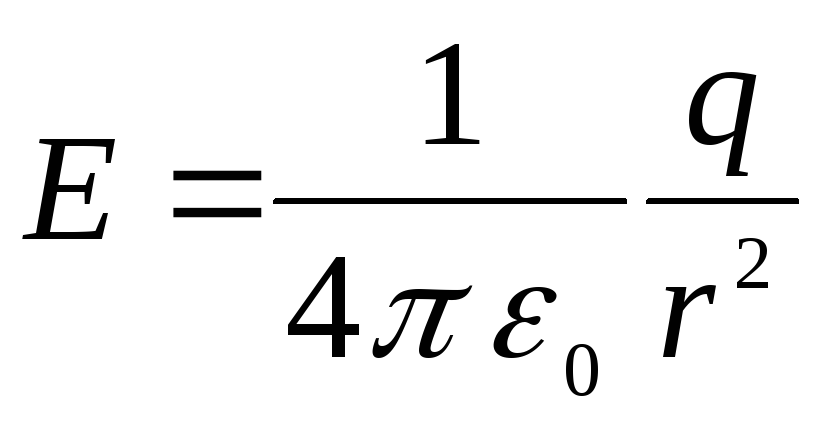
і, отже, змінюється у просторі як і, як і разі поля точкового заряду, звідки випливає, що різницю потенціалів між внутрішньої сферою і якою – або точкою поля, віддаленої відстань rвід центру конденсатора, дорівнює
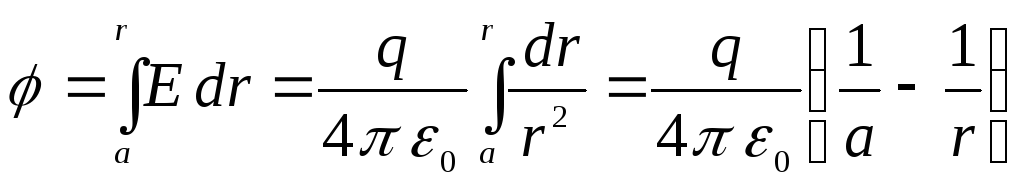 .
.
Різниця потенціалів 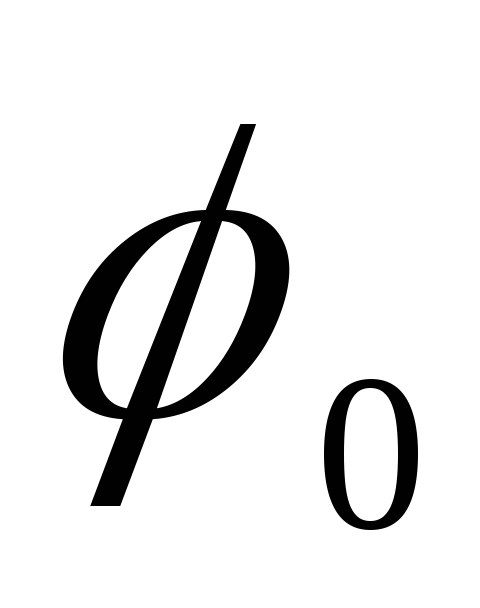 між електродами (сферами) дорівнюватиме
між електродами (сферами) дорівнюватиме
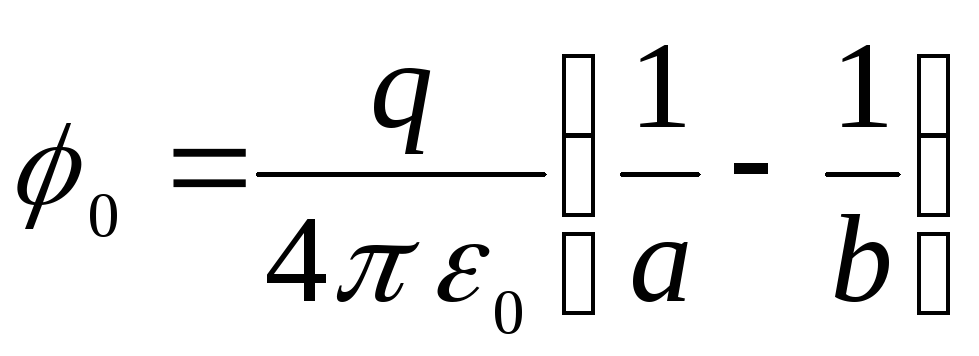 .
.
З цих двох формул випливає
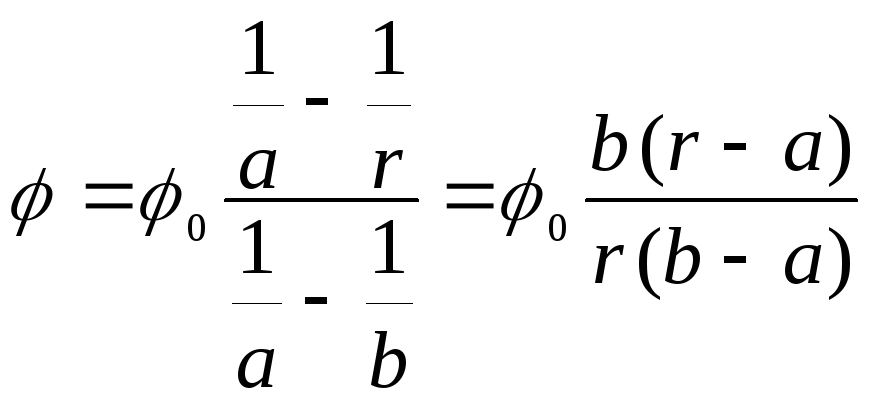 .
.
Вимірявши 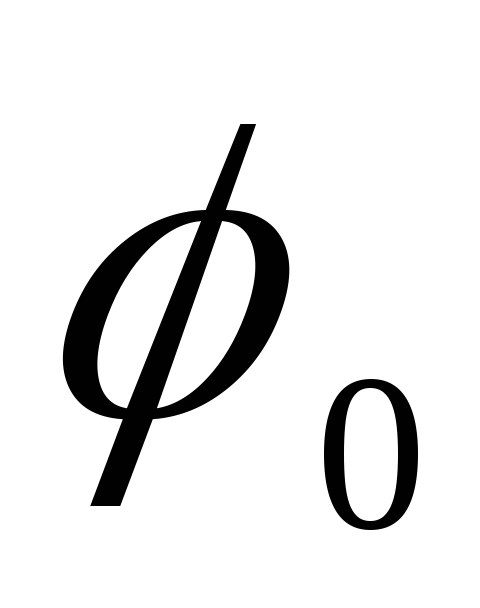 між електродами можна обчислити потенціал будь-якої точки поля.
між електродами можна обчислити потенціал будь-якої точки поля.
7.2. Нехай система зарядів 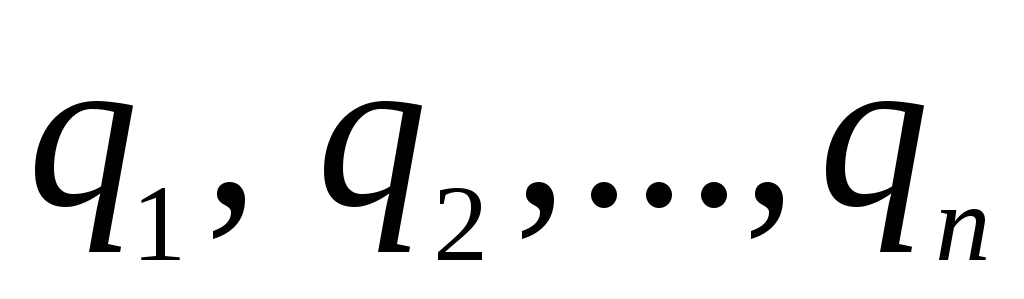 перебуває у обсязі з лінійними розмірами l. Знайдемо потенціал поля, створюваного цією системою зарядів з відривами r, більших проти l. Виберемо початок координат O всередині об'єму, який займає система зарядів, та визначимо положення зарядів за допомогою радіусів – векторів
перебуває у обсязі з лінійними розмірами l. Знайдемо потенціал поля, створюваного цією системою зарядів з відривами r, більших проти l. Виберемо початок координат O всередині об'єму, який займає система зарядів, та визначимо положення зарядів за допомогою радіусів – векторів 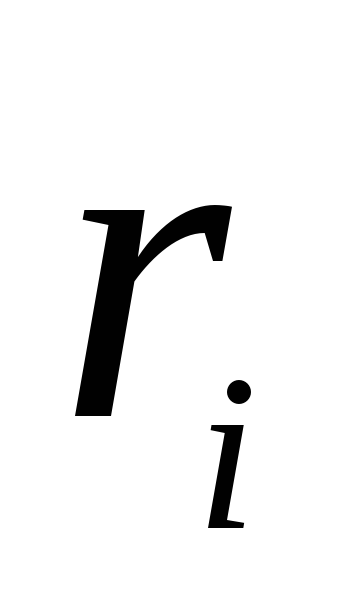 (на малюнку ___ показаний один із радіус – векторів
(на малюнку ___ показаний один із радіус – векторів 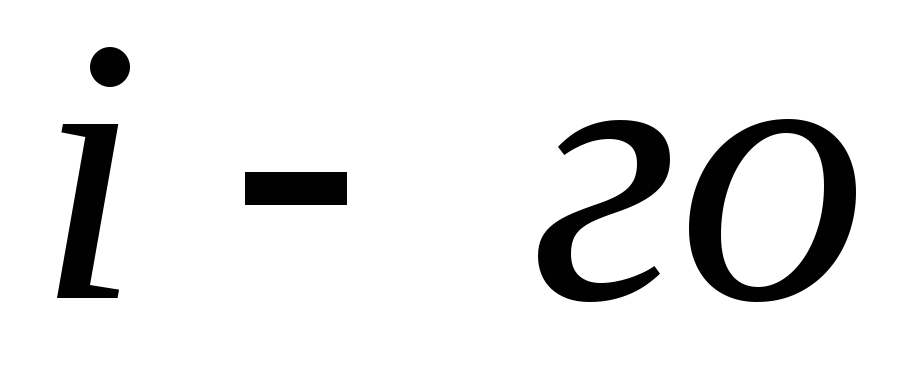 заряду). Потенціал у точці, що визначається радіус – вектором
заряду). Потенціал у точці, що визначається радіус – вектором 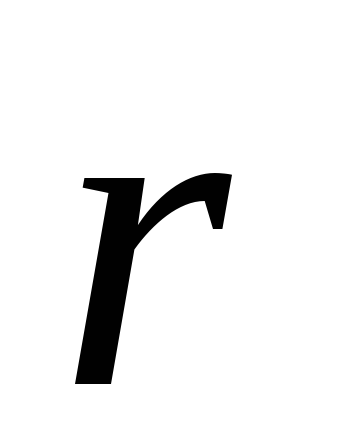 , дорівнює
, дорівнює
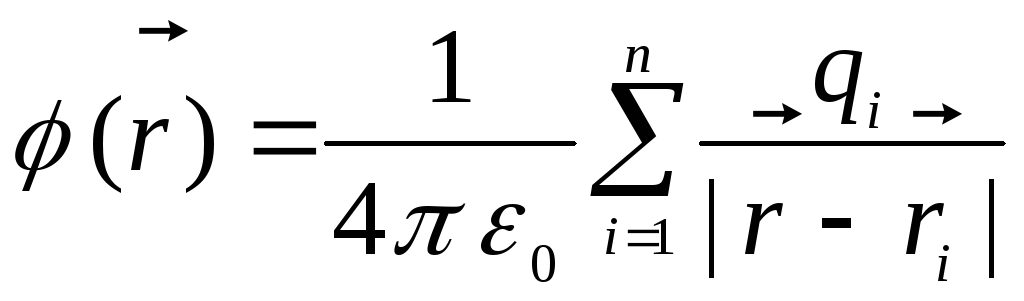 .
.
Так як 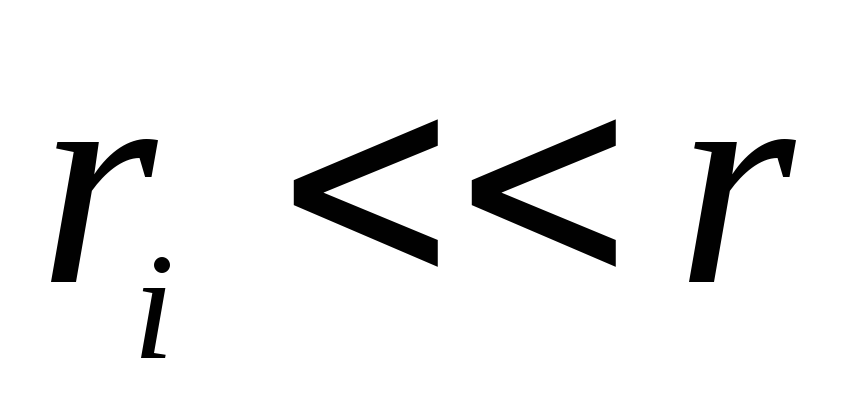 , то можна покласти, що
, то можна покласти, що
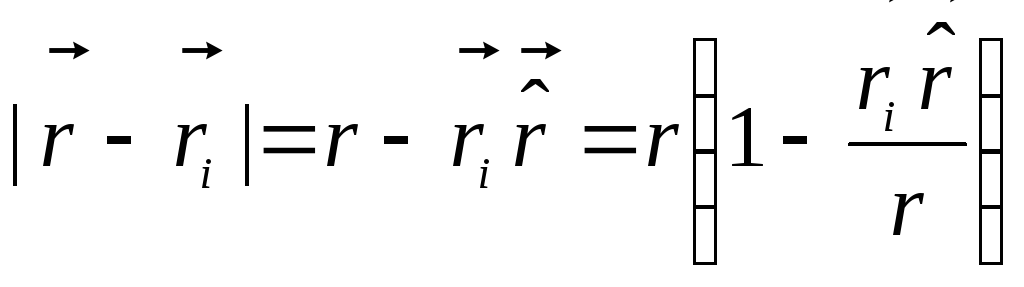
(Символом 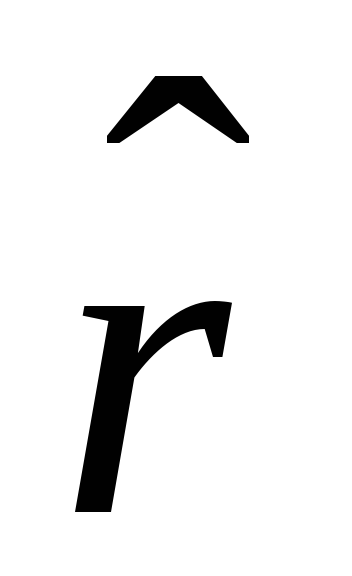 ми окреслили одиничний вектор). Тоді
ми окреслили одиничний вектор). Тоді
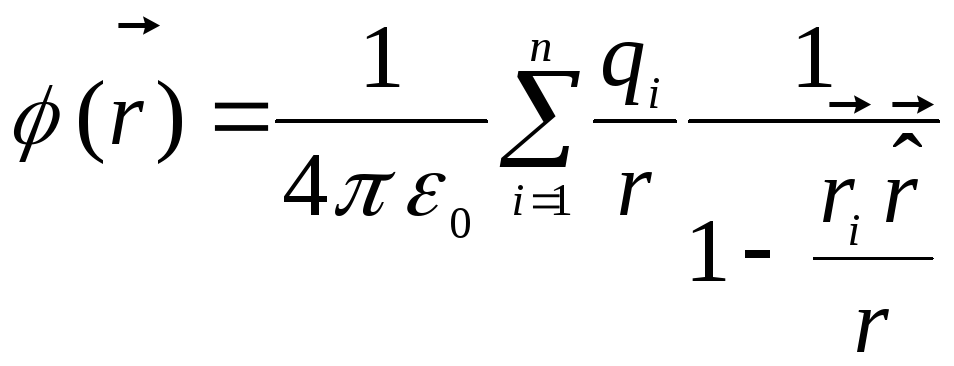 .
.
Скористаємося формулою
![]()
при 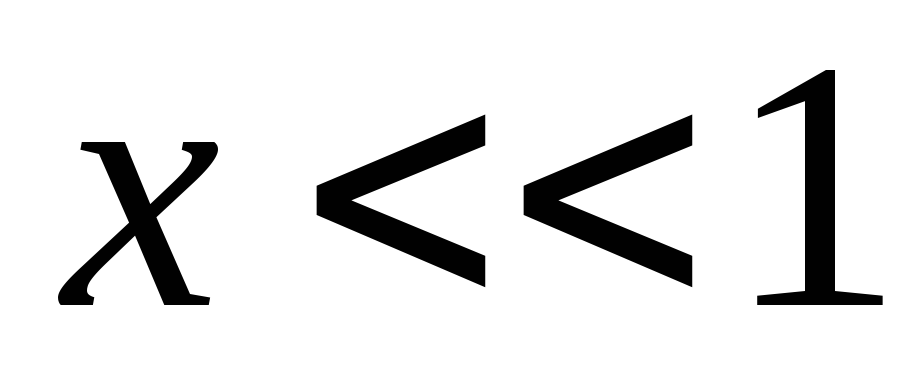 .
.
Тепер ми можемо записати
Перший член цього виразу є потенціал поля точкового заряду величиною 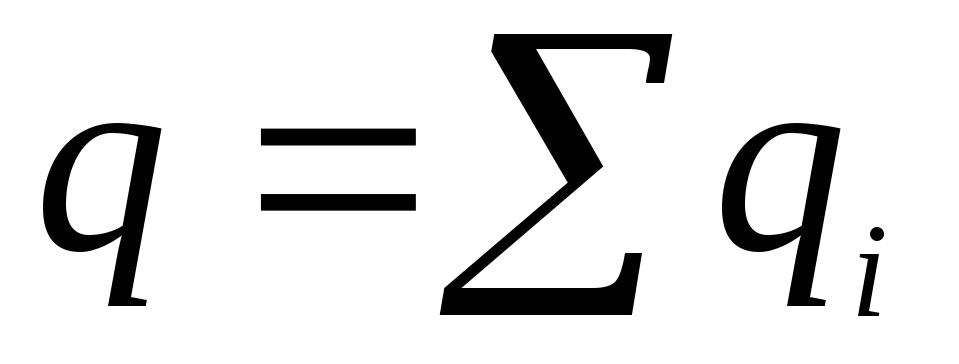 . Другий член такого ж виду як вираз, що визначає потенціал поля диполя. Роль електричного моменту диполя відіграє
. Другий член такого ж виду як вираз, що визначає потенціал поля диполя. Роль електричного моменту диполя відіграє
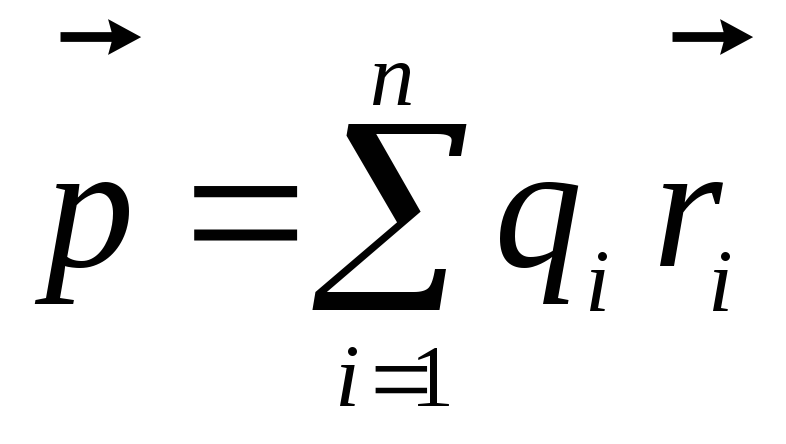 ,
,
яку називають дипольним електричним моментом системи зарядів.
7.3. Якщо поле створене кількома зарядами, то потенціал цього поля дорівнює сумі потенціалів полів, створених окремими зарядами.
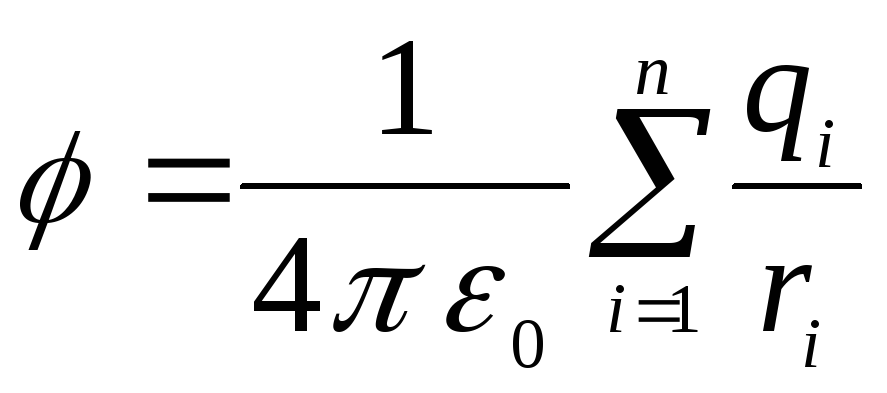
Тут  - потенціал результуючого поля в точці, що розглядається щодо нескінченності,
- потенціал результуючого поля в точці, що розглядається щодо нескінченності, 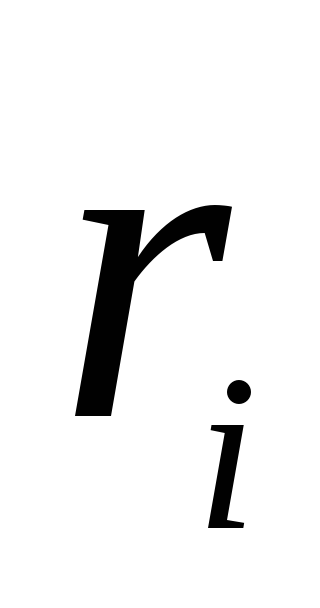 - Відстань від цієї точки до
- Відстань від цієї точки до 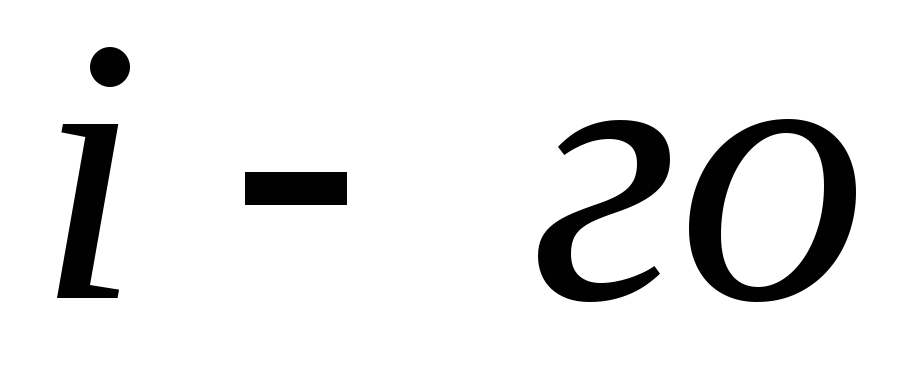 заряду, а підсумовування проводиться у всіх точкових зарядах.
заряду, а підсумовування проводиться у всіх точкових зарядах.
Розглянуте поле має осьову симетрію, тому картина поля в будь-якій площині, що проходить через вісь диполя, буде однією і тією ж, а вектор  лежить у цій площині. Положення точки M щодо диполя характеризуватимемо за допомогою радіус – вектора
лежить у цій площині. Положення точки M щодо диполя характеризуватимемо за допомогою радіус – вектора 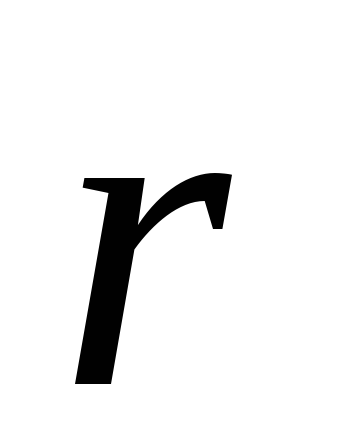 , або за допомогою полярних координат r і
, або за допомогою полярних координат r і  . Положення заряду
. Положення заряду 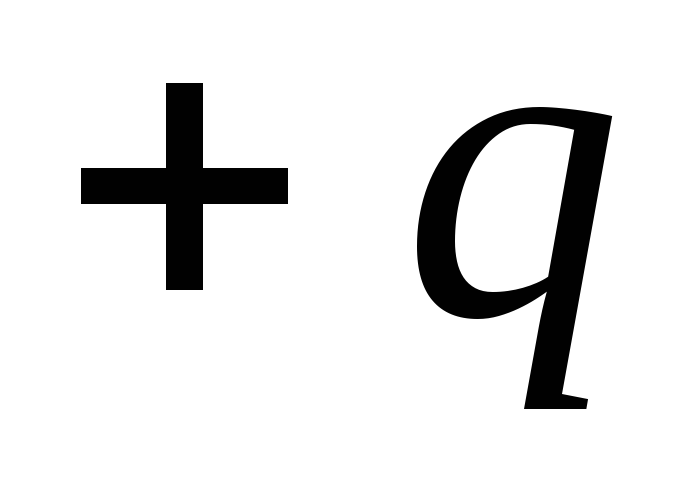 щодо центру диполя визначимо вектором
щодо центру диполя визначимо вектором  , а заряду
, а заряду 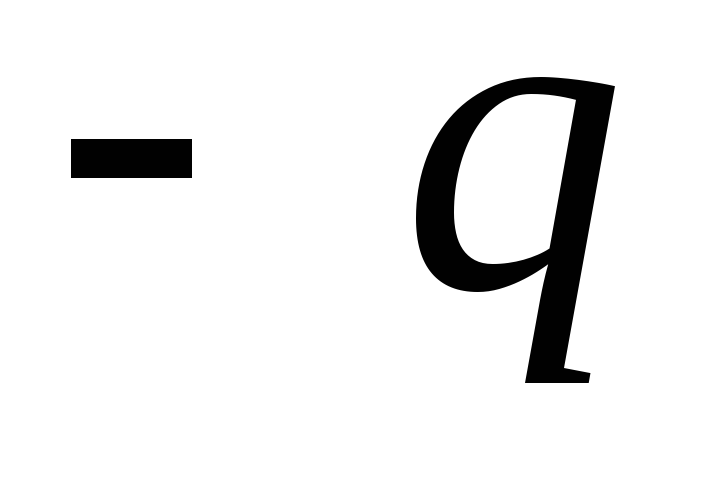 – вектором
– вектором 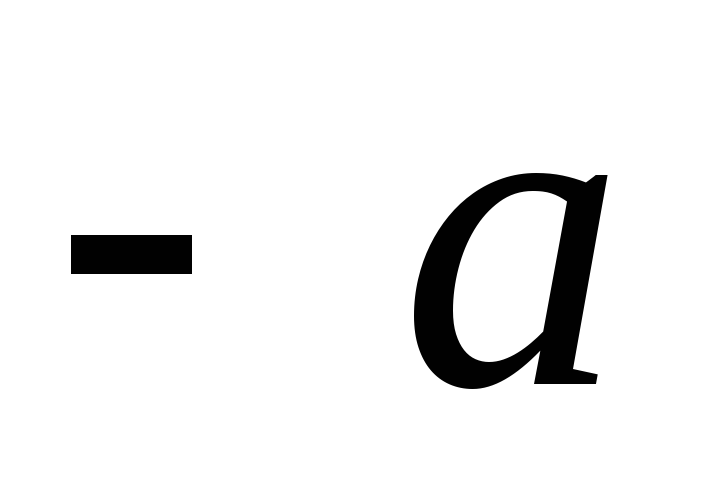 . Очевидно, що
. Очевидно, що 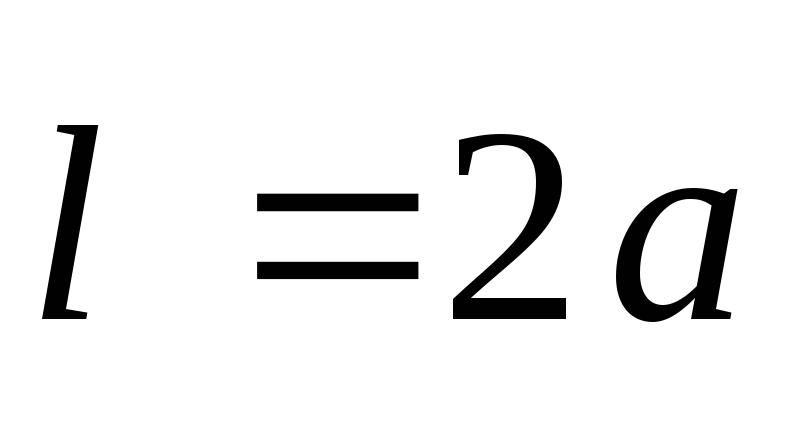 , де
, де 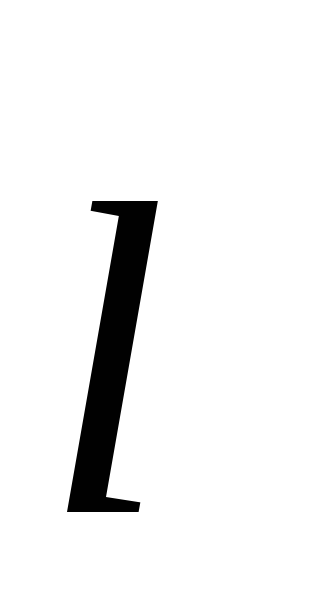 – плече диполя. Відстань від зарядів
– плече диполя. Відстань від зарядів 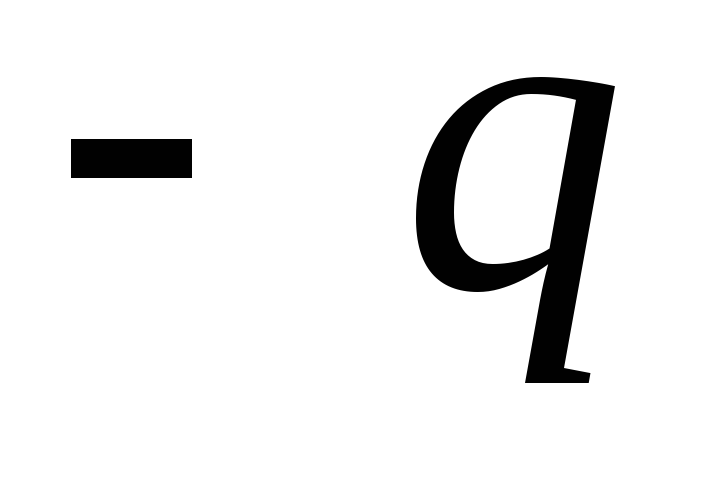 і
і 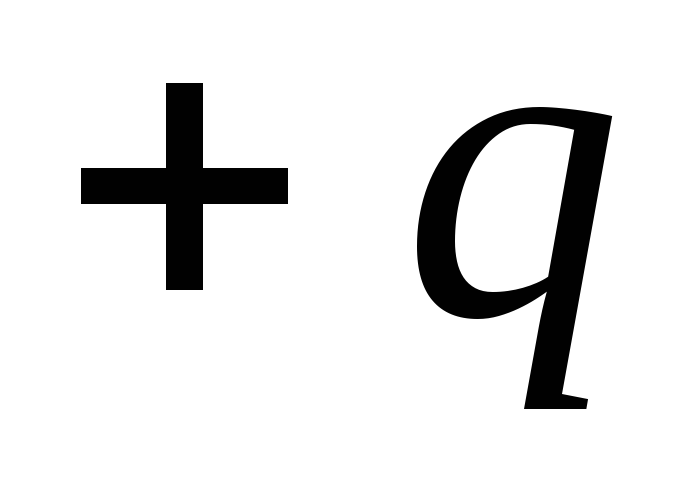 до обраної точки M позначимо відповідно
до обраної точки M позначимо відповідно 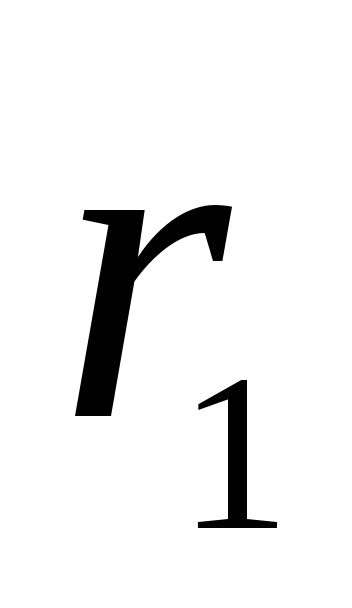 і
і 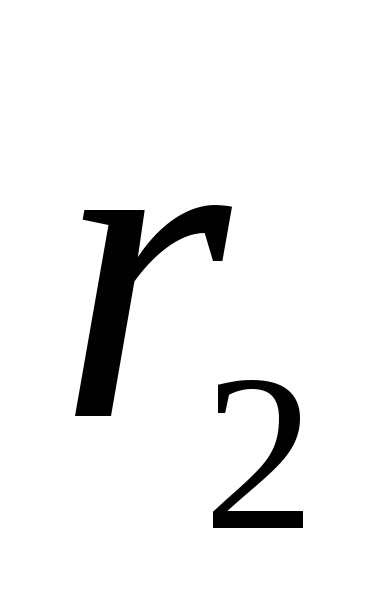 . Так як
. Так як 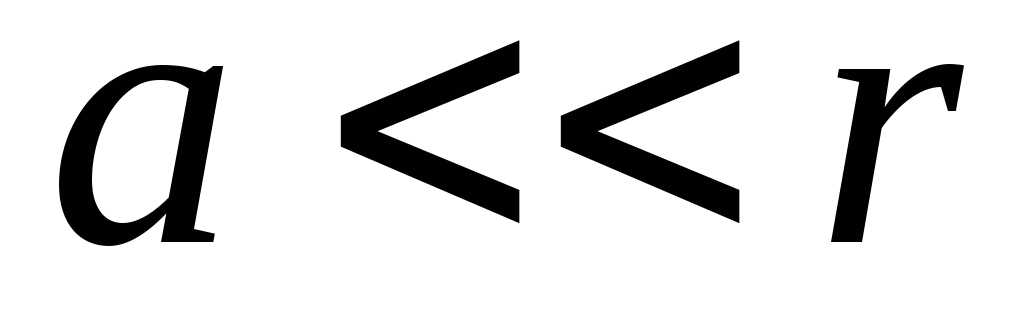 , то можна покласти, що
, то можна покласти, що
Потенціал у точці, що визначається радіус – вектором 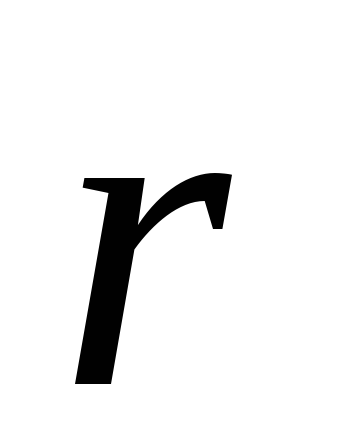 , дорівнює
, дорівнює
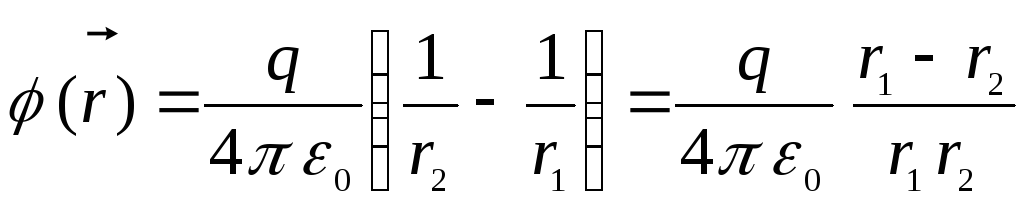 .
.
твір 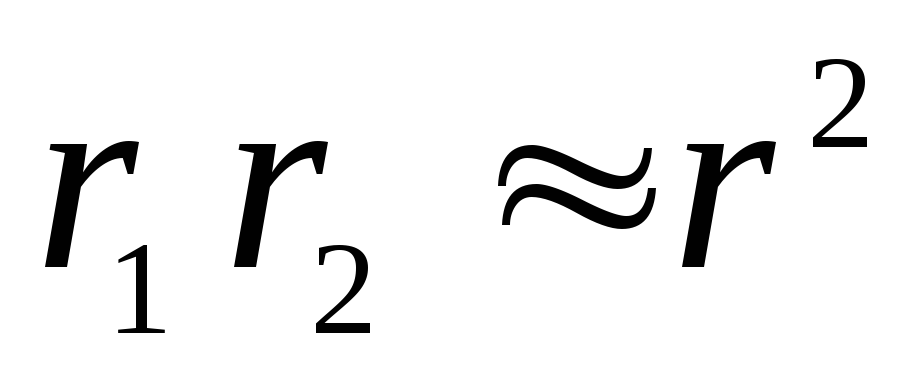 , Різниця
, Різниця 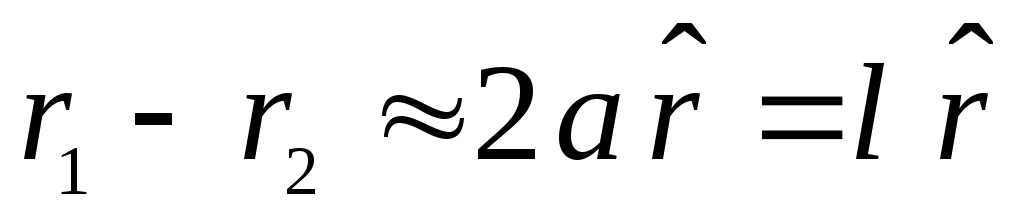 . Отже,
. Отже,
![]() ,
,
де 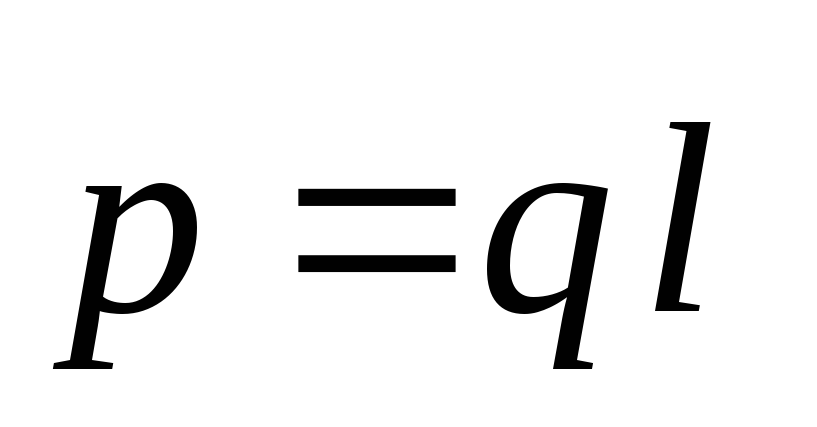 - Електричний момент диполя.
- Електричний момент диполя.
З цієї формули видно, що потенціал поля диполя визначається його електричним моментом. Порівнюючи потенціал поля диполя з потенціалом поля точкового заряду, видно, що потенціал поля диполя зменшується з відстанню швидше 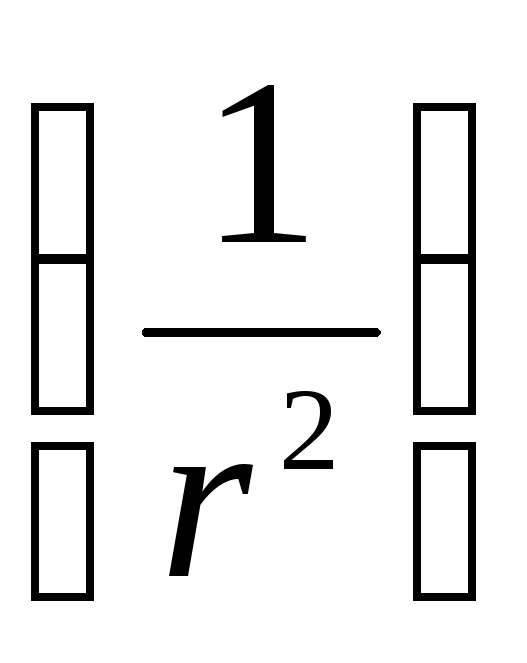 , ніж потенціал поля точкового заряду
, ніж потенціал поля точкового заряду 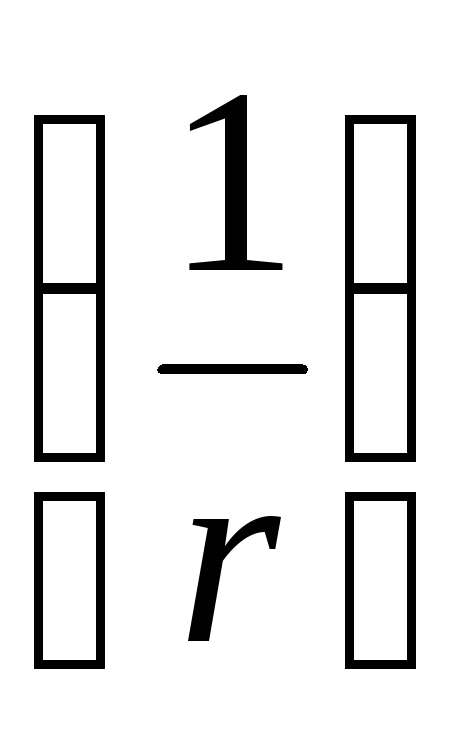 .
.
З малюнка ___ видно, що 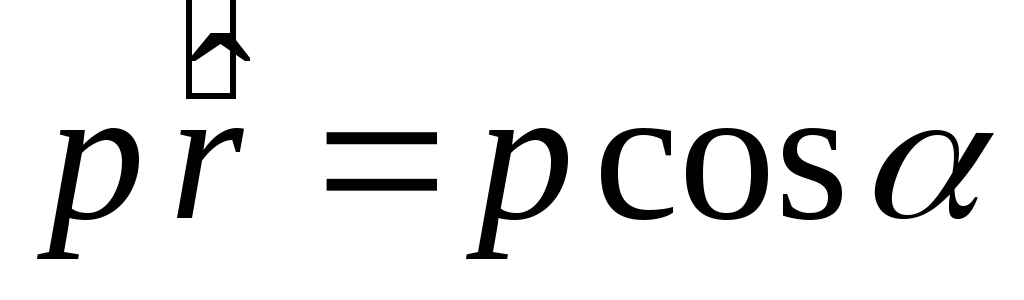 . Тому
. Тому
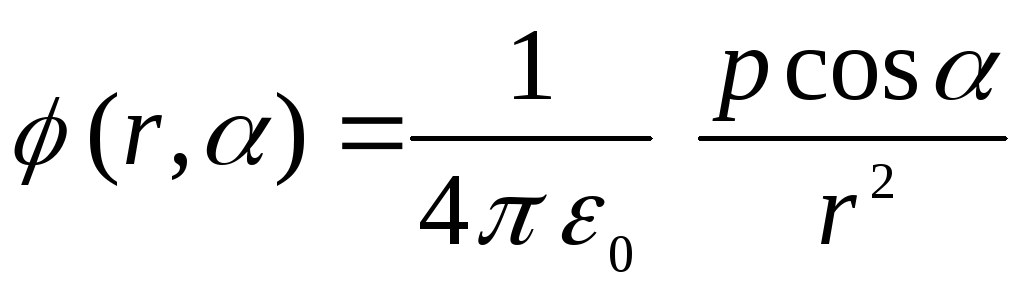 .
.
7.4. Нехай внутрішня сфера, радіус якої  має позитивний заряд
має позитивний заряд 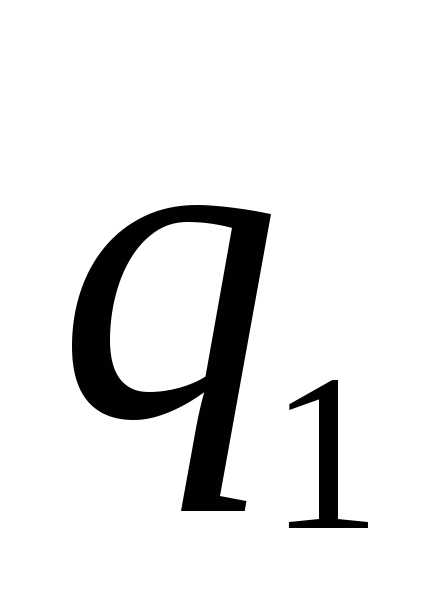 , а зовнішня з радіусом
, а зовнішня з радіусом 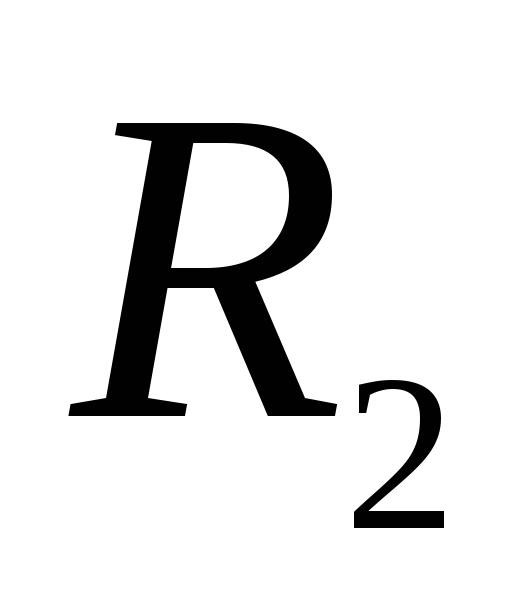 - Негативний заряд
- Негативний заряд 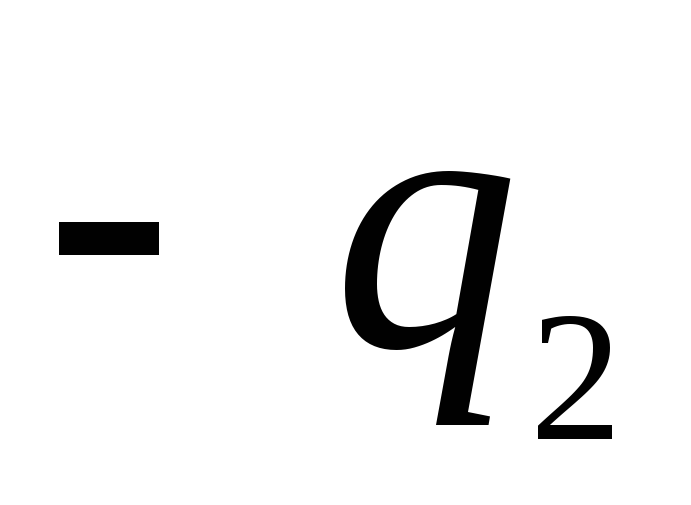 , причому
, причому 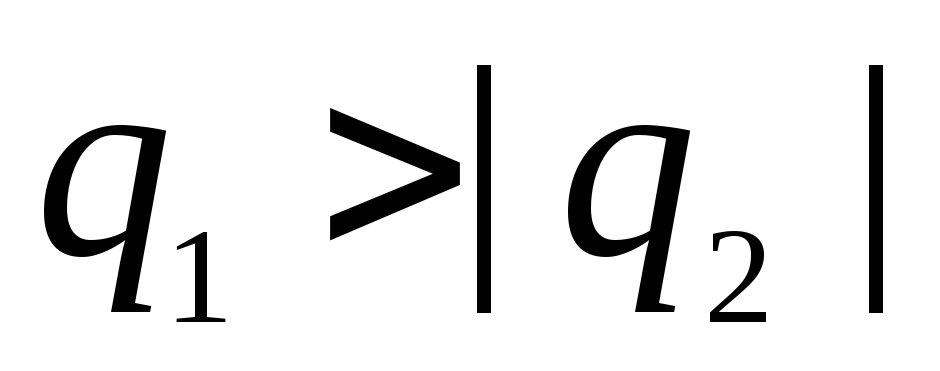 .
.
Поза сферами потенціал буде дорівнювати
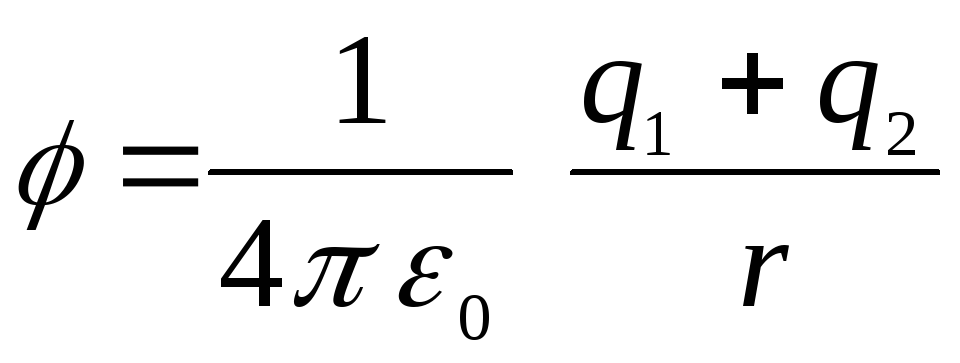 ,
,
тому що його створюють спільно обидві сфери (потенціал є робота зовнішніх сил, що здійснюється при переміщенні одиничного позитивного заряду з нескінченності в дану точку поля). Робота з переміщення одиничного позитивного заряду з нескінченності в область між сферами дорівнюватиме сумі двох робіт: 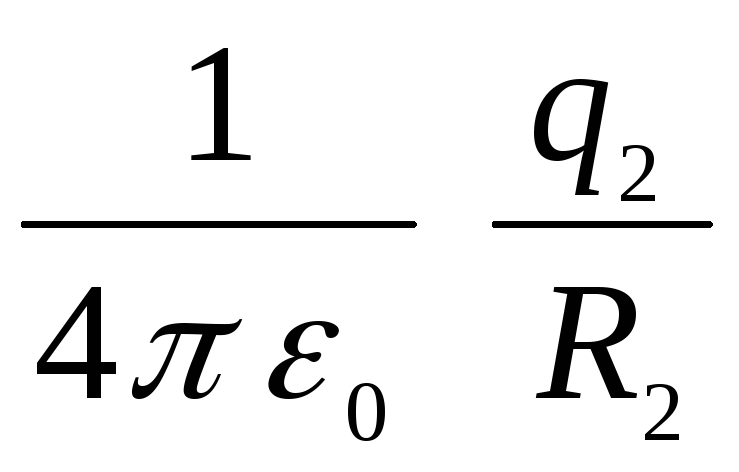 (роботі проти сил, що діють з боку зовнішньої сфери на шляху з нескінченності до її поверхні) та
(роботі проти сил, що діють з боку зовнішньої сфери на шляху з нескінченності до її поверхні) та 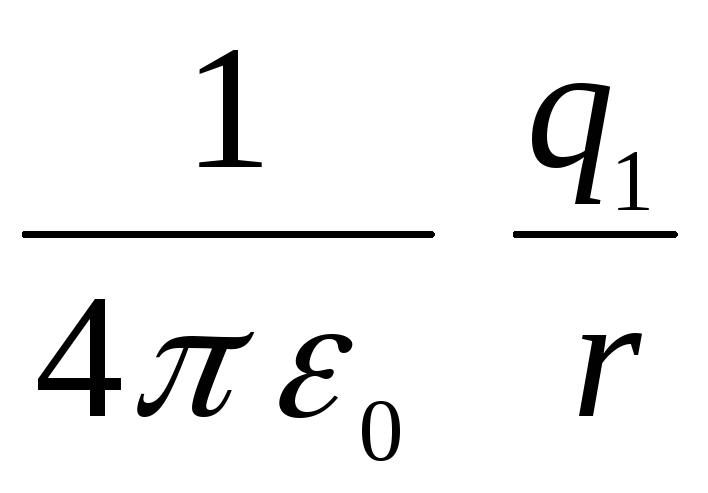 (Роботі проти поля внутрішньої сфери), тобто.
(Роботі проти поля внутрішньої сфери), тобто.
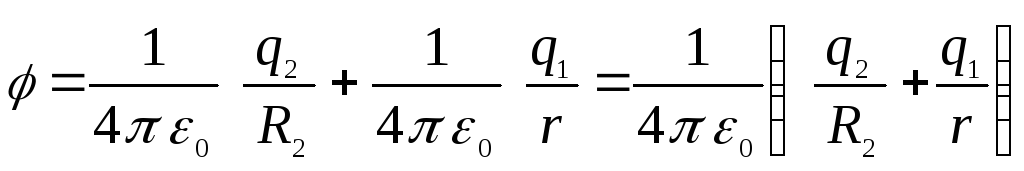 .
.
Усередині меншої сфери потенціал буде постійний і дорівнює
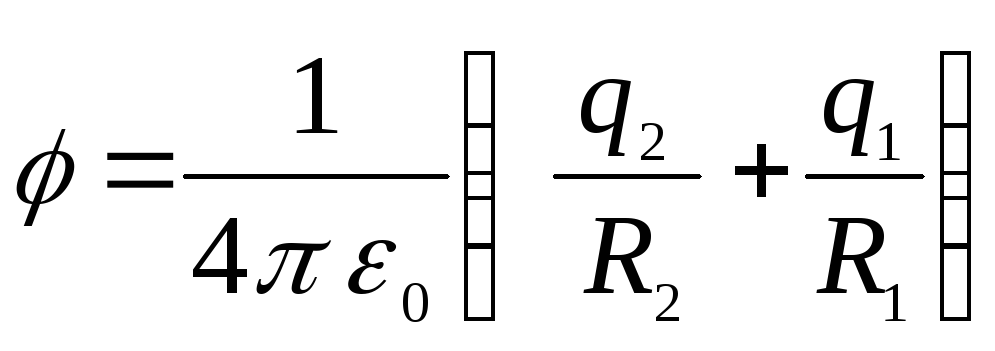 .
.
Графік, побудований за першою та другою формулами, зображений на малюнку ____1.
Якщо заряди сфер дорівнюють за величиною і протилежні за знаком, тобто. 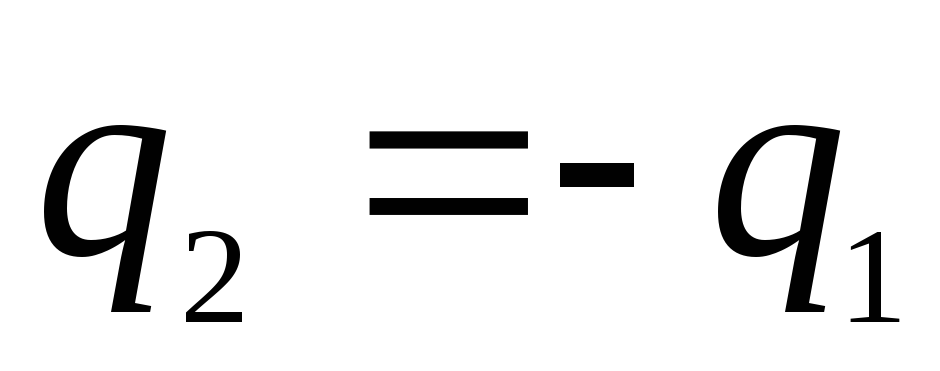 (така система називається сферичним конденсатором), то потенціал у зовнішній області перетворюється на нуль, а між обкладками дорівнює
(така система називається сферичним конденсатором), то потенціал у зовнішній області перетворюється на нуль, а між обкладками дорівнює
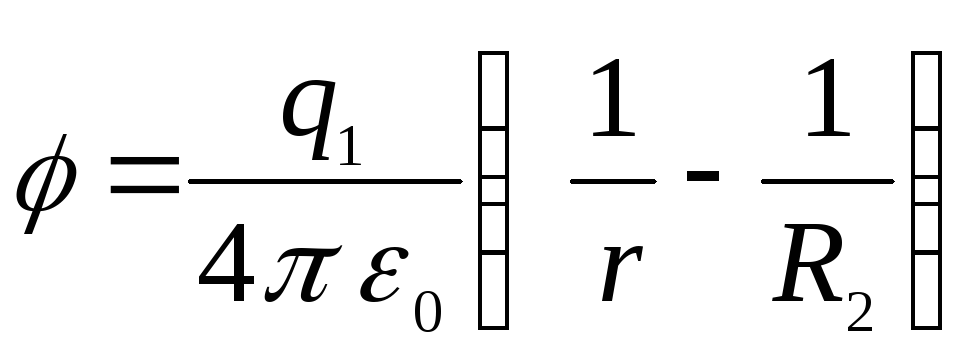 .
.
Виходить графік, зображений малюнку ___2.
Якщо внутрішня сфера має негативний заряд, а зовнішня – позитивний, то графік перевертається і так, як зображено малюнку ____3.
7.5. Інтегрування рівняння Пуассона у сферичні координати. Введемо сферичну систему координат 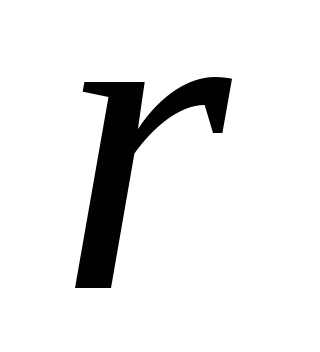 ,
, ,
, , Взявши за початок відліку центр кулі. Рівняння Гауса в диференціальній формі (рівняння Пуассона), що визначає потенціал поля, набуває вигляду
, Взявши за початок відліку центр кулі. Рівняння Гауса в диференціальній формі (рівняння Пуассона), що визначає потенціал поля, набуває вигляду
де 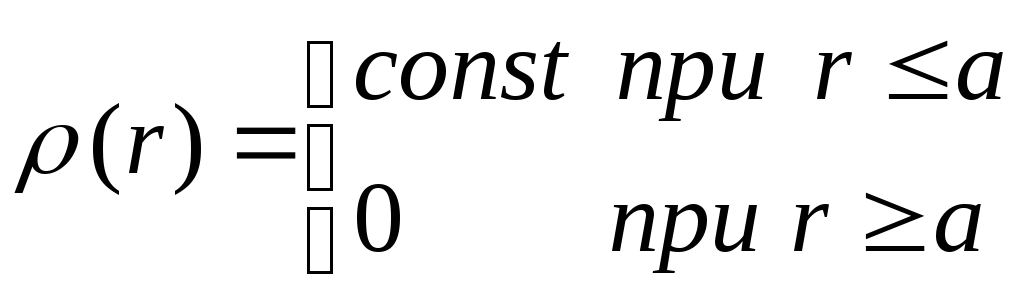 .
.
Внаслідок сферично-симетричного розподілу зарядів, потенціал  залежить тільки від відстані r і не залежить від кутів
залежить тільки від відстані r і не залежить від кутів  і
і  , тобто.
, тобто. 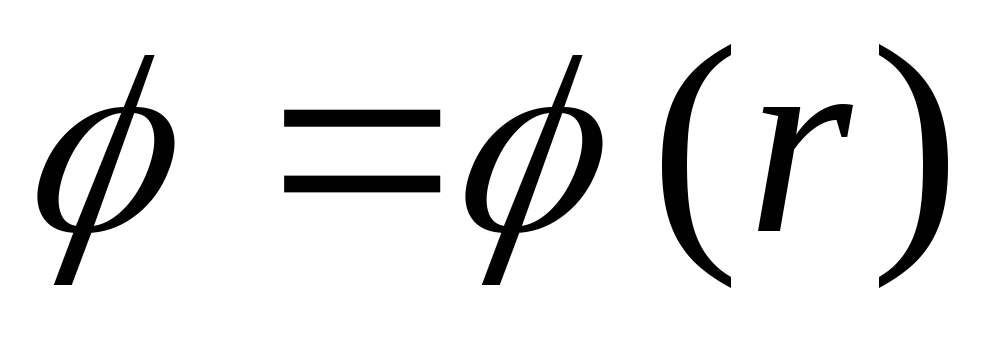 . Тому рівняння Пуассона спрощиться і набуває вигляду
. Тому рівняння Пуассона спрощиться і набуває вигляду
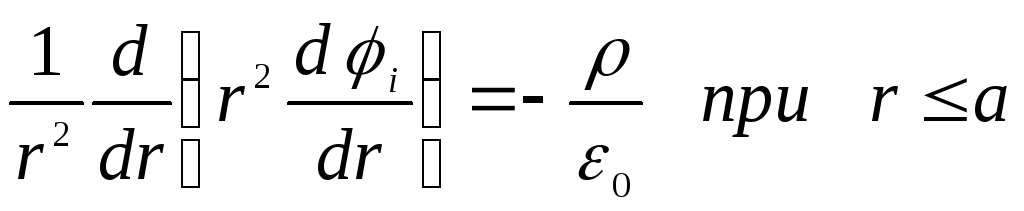
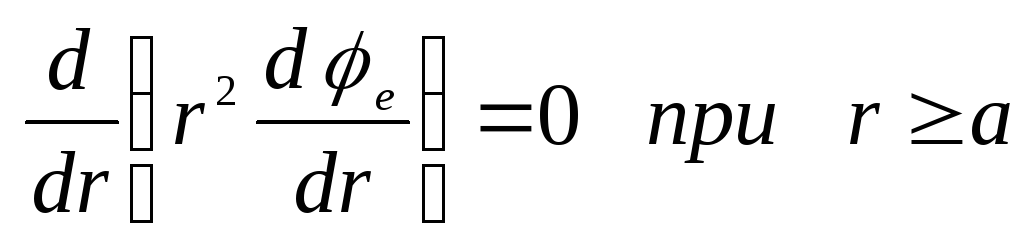 .
.
Тут через 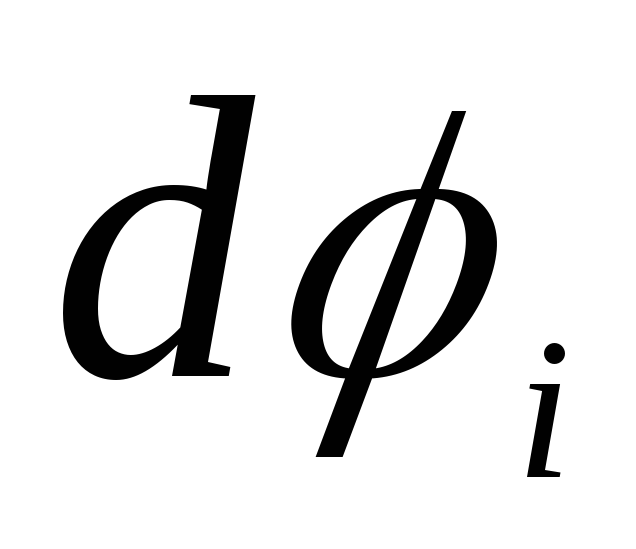 позначений потенціал усередині кулі, а через
позначений потенціал усередині кулі, а через 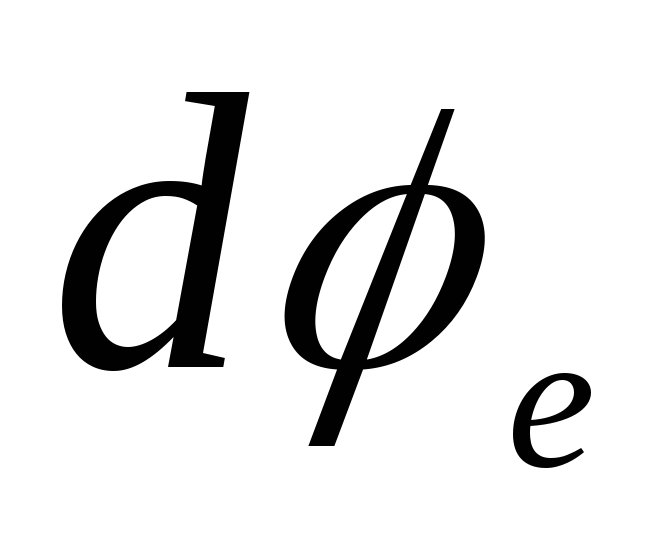 – поза кулею. Інтегруючи ці рівняння, знаходимо
– поза кулею. Інтегруючи ці рівняння, знаходимо
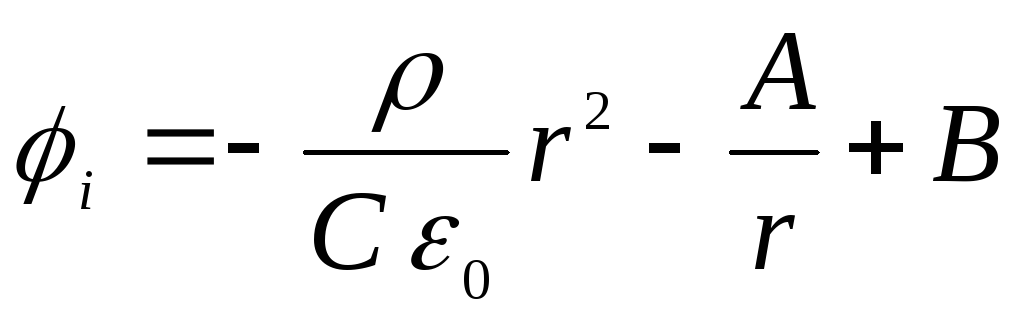 ,
,
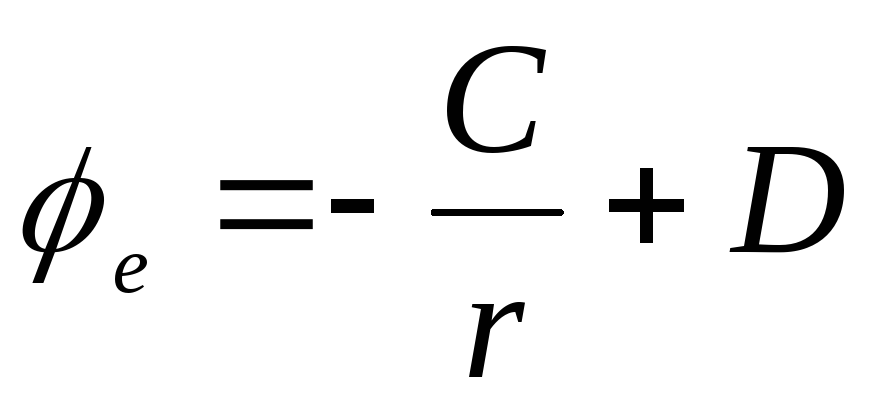 .
.
Постійні A, B, C, D мають бути визначені з наступних граничних умов.
1) Потенціал  повинен залишатися кінцевим при
повинен залишатися кінцевим при 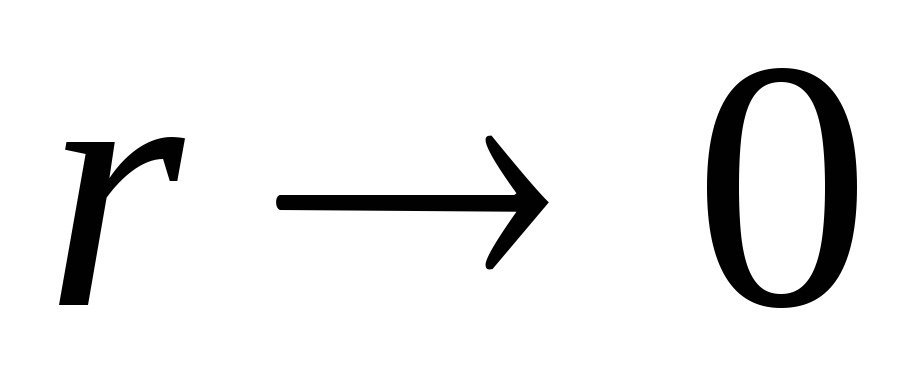 , звідки безпосередньо випливає, що
, звідки безпосередньо випливає, що 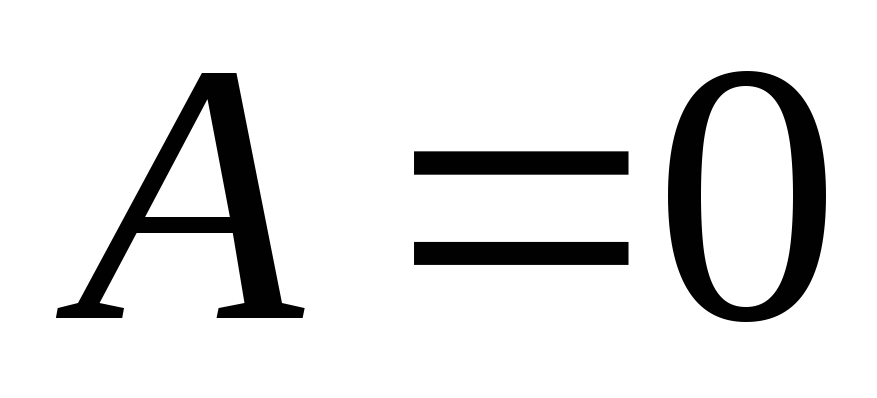 .
.
2)
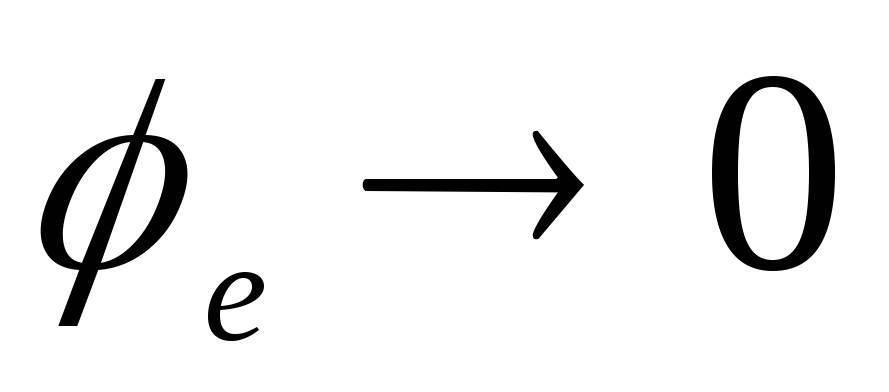 при
при  звідки випливає, що
звідки випливає, що 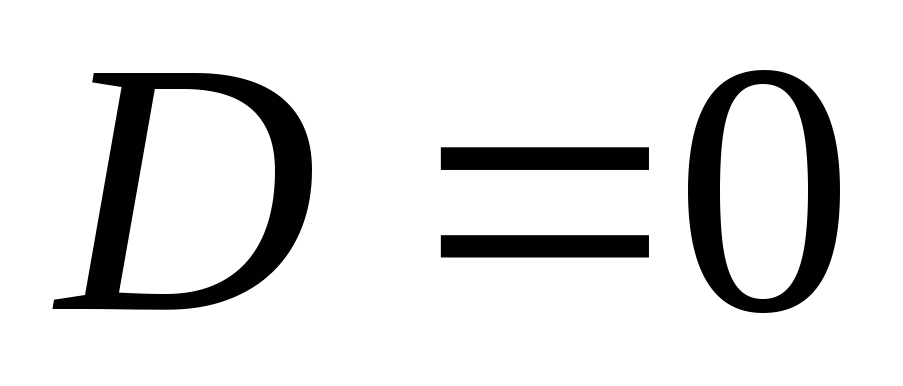 .
.
3) Потенціал електростатичного поля є безперервною функцією координат, тому необхідно, щоб 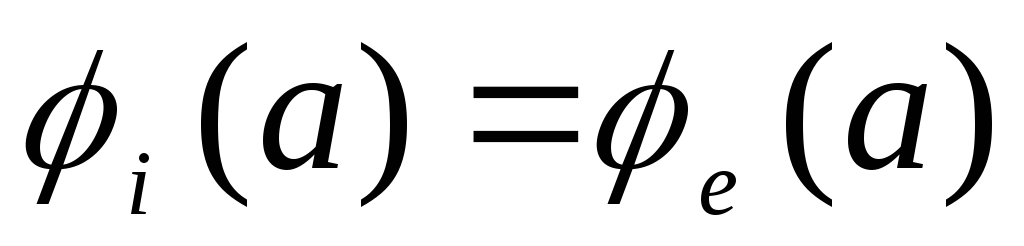 .
.
4) Нормальна складова вектора  має відчувати стрибка під час проходження через поверхню кулі, тобто.
має відчувати стрибка під час проходження через поверхню кулі, тобто. 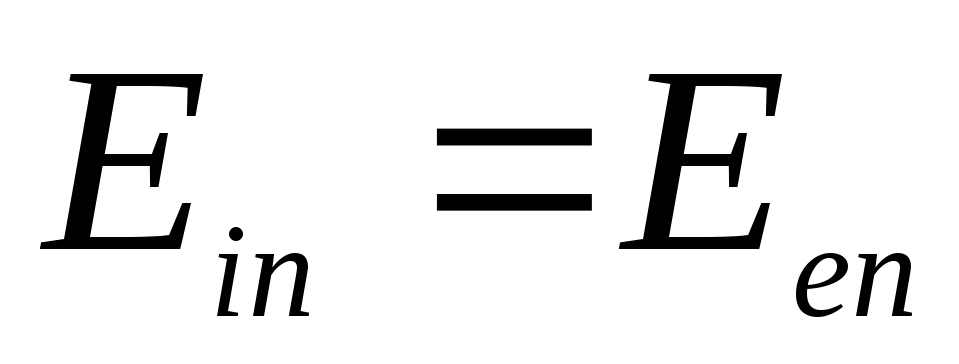 при
при 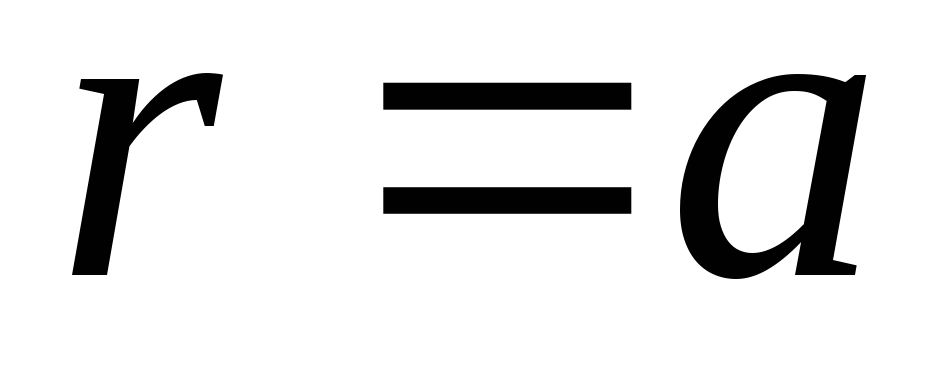 так як поверхнева щільність заряду на поверхні кулі дорівнює нулю. Остання умова еквівалентна вимогі
так як поверхнева щільність заряду на поверхні кулі дорівнює нулю. Остання умова еквівалентна вимогі
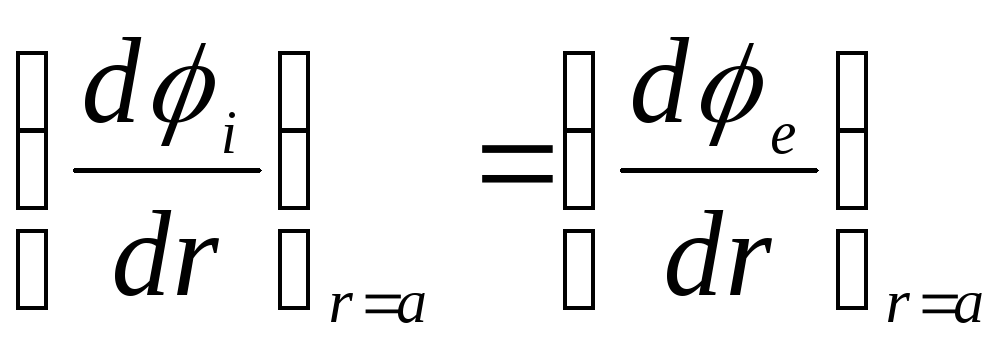 .
.
З останніх двох умов знаходимо
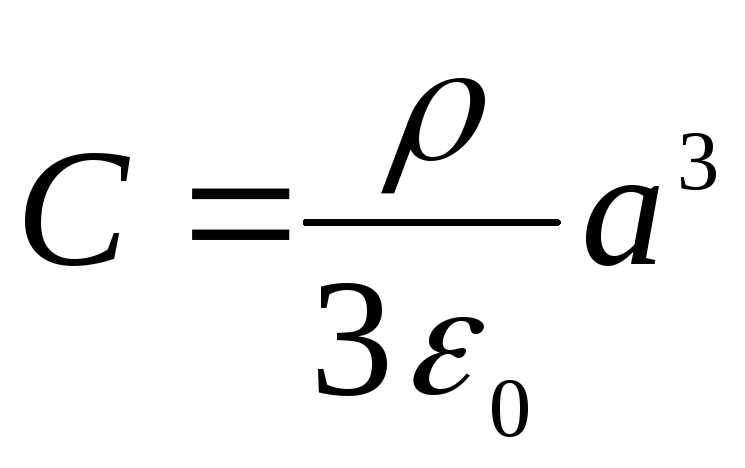 ,
,
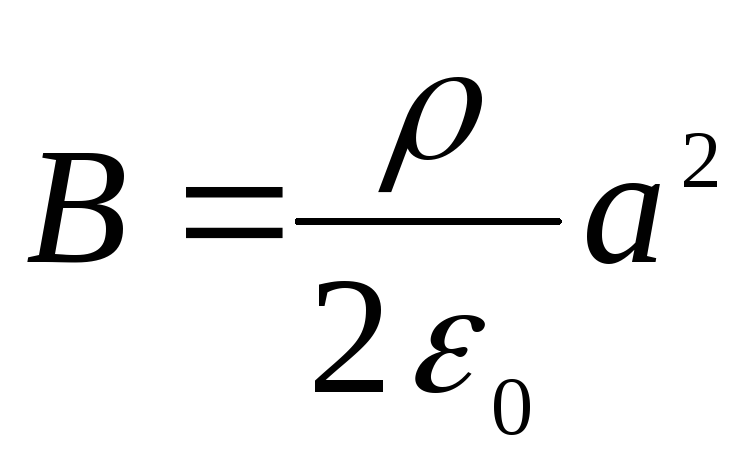 .
.
Шукані потенціали остаточно запишемо у вигляді
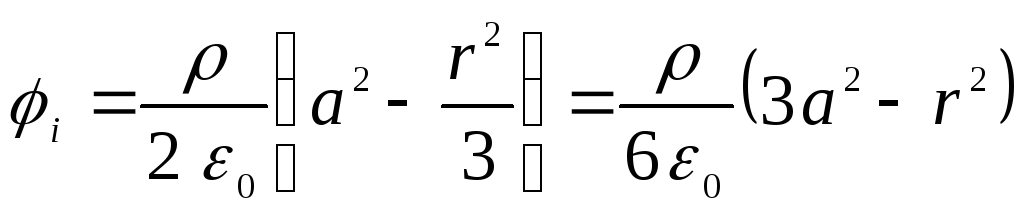 ,
,
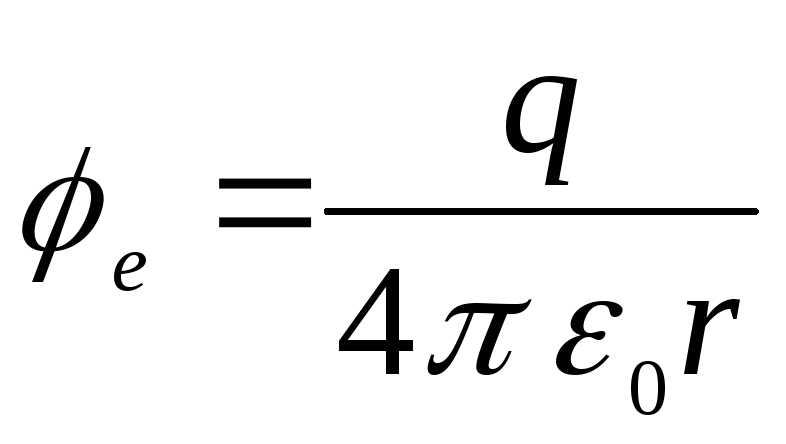 .
.
З цих формул видно, що поза кулею потенціал поля аналогічний до поля точкового заряду.
Зобразимо графік 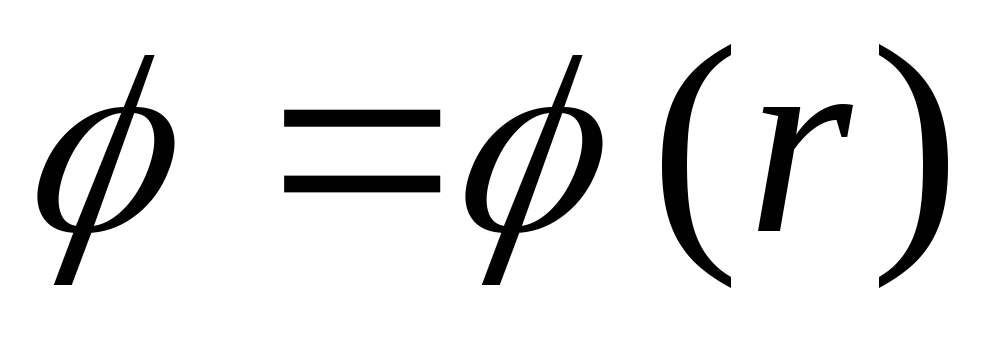 .
.
Нехай 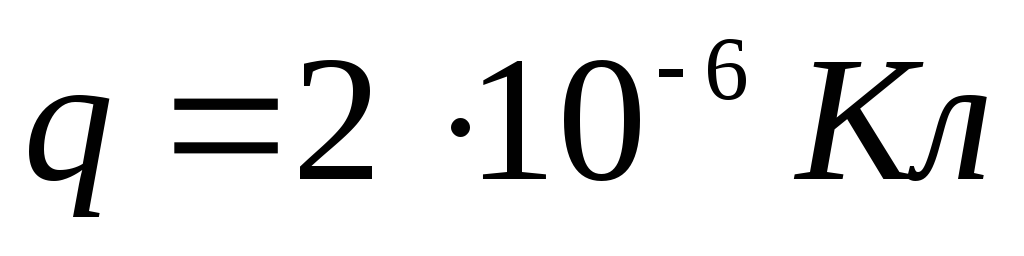 ,
,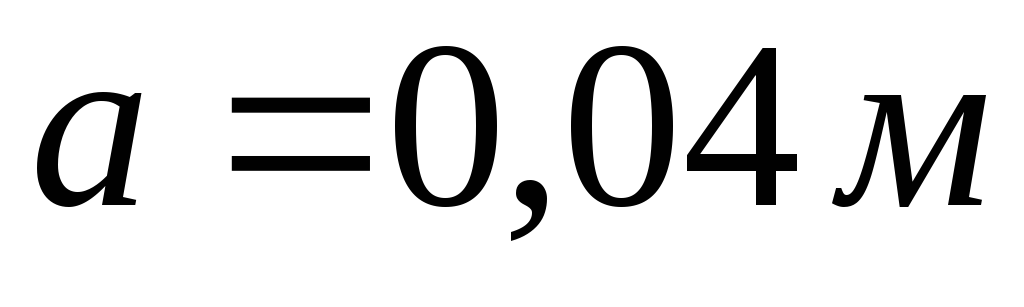 . Знайдемо об'ємну щільність заряду
. Знайдемо об'ємну щільність заряду
та відношення
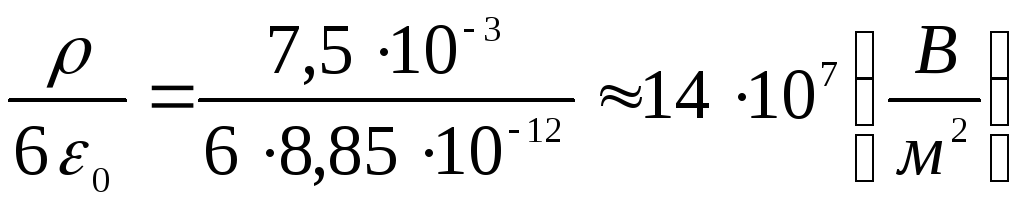 .
.
Тепер можна записати, що потенціал усередині сфери
Складемо таблицю
|
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Потенціал поза сферою 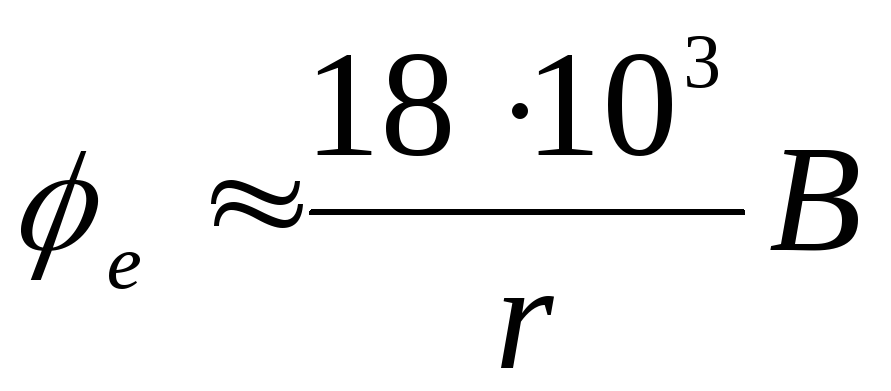 .
.
|
| |||||||
|
|
|
|
|
|
|
|
|
Тепер будуємо графік 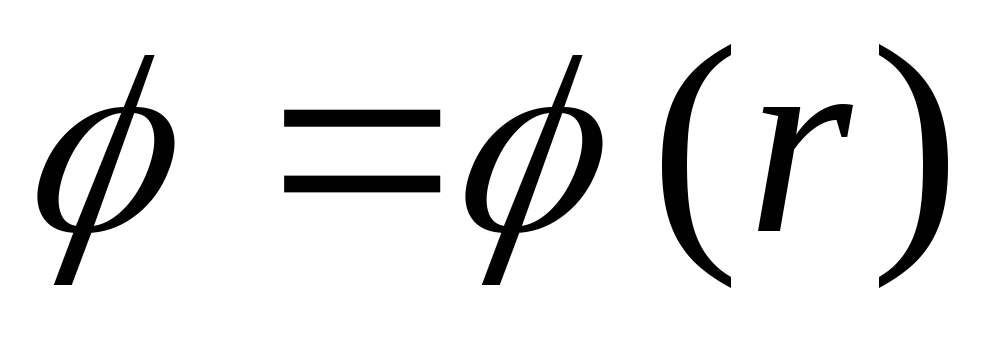 .
.
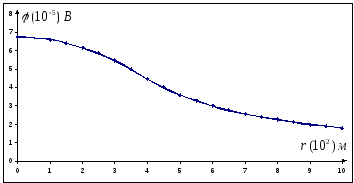
Зв'язок між напруженістю та потенціалом.
Залежність напруженості електростатіічного поля від відстані до центру кулі всередині кулі має вигляд (див. розв'язання задачі 1.5.4.)
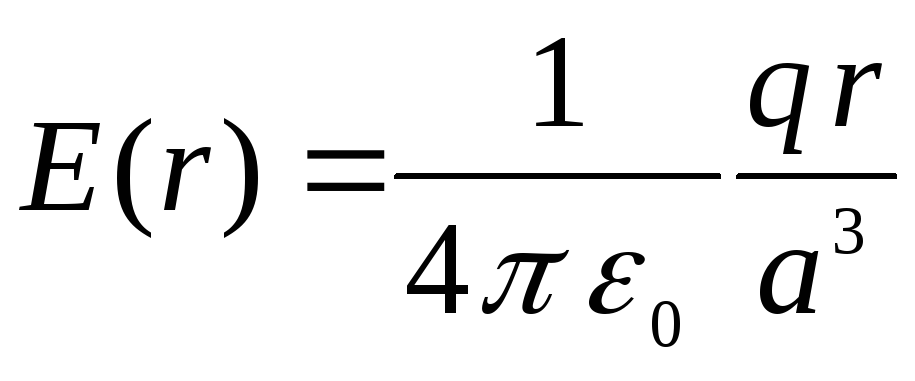 ,
,
тобто. всередині кулі напруженість поля росте лінійно з відстанню від центру. При 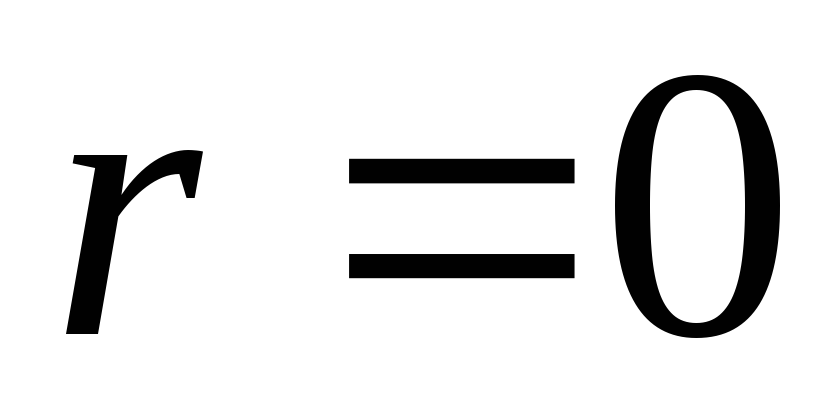 ,
,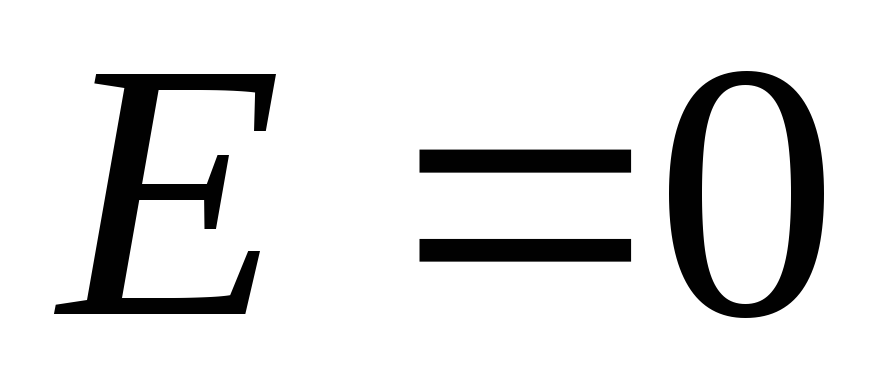 , при
, при 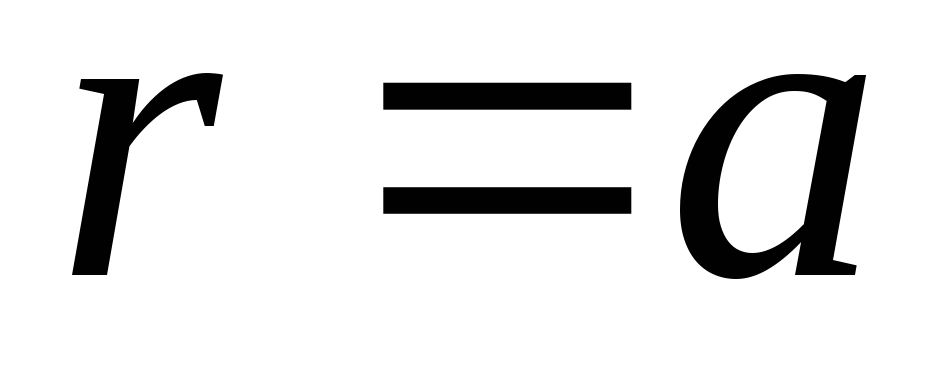 вона досягає максимуму і стає рівною
вона досягає максимуму і стає рівною
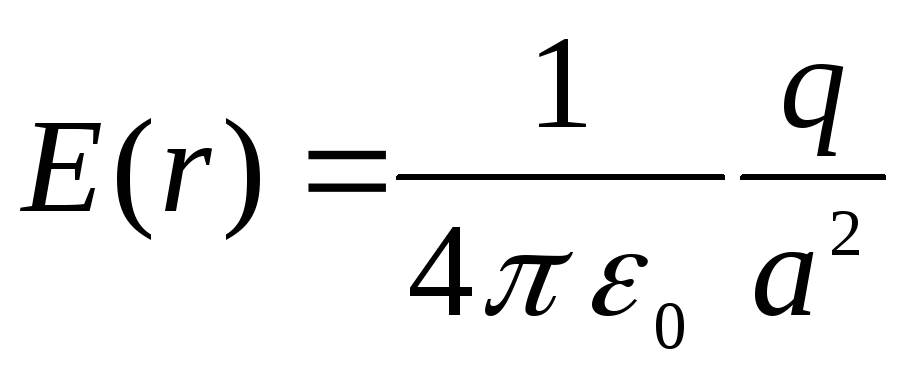 .
.
При  Напруженість поля залежить від відстані як напруженість поля точкового заряду.
Напруженість поля залежить від відстані як напруженість поля точкового заряду.
Зміна потенціалу у полі зарядженої кулі
Потенціал поля всередині кулі
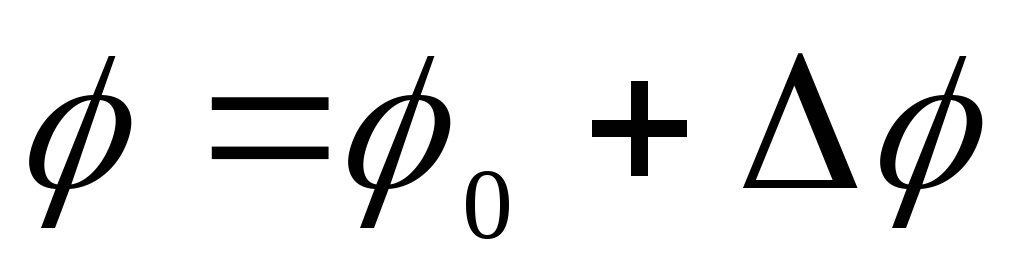 ,
,
де 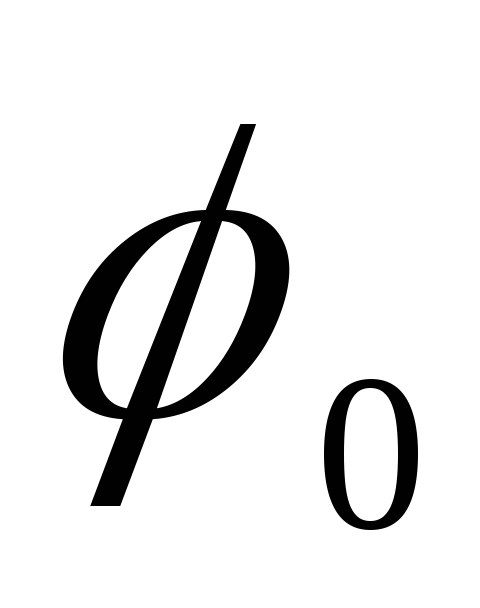 - Потенціал точки на поверхні кулі (потенціал поля точкового заряду), рівний
- Потенціал точки на поверхні кулі (потенціал поля точкового заряду), рівний
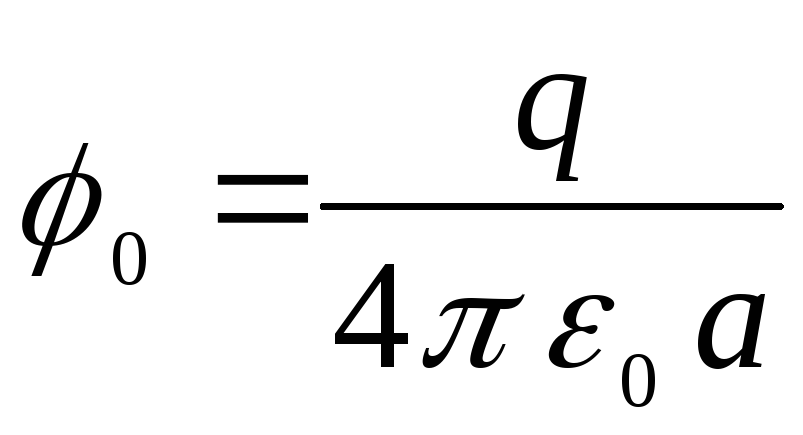 .
.
Остаточно отримаємо
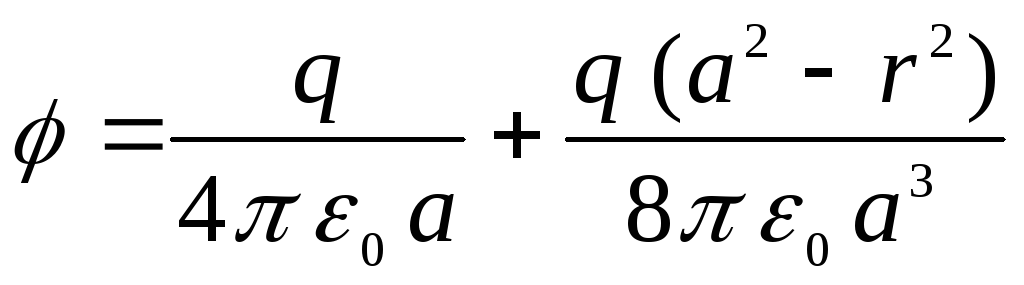 .
.
Враховуючи, що об'ємна щільність заряду
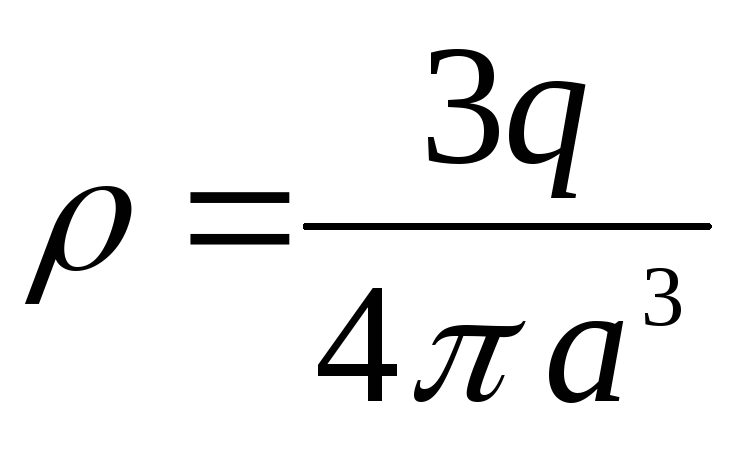 ,
,
можна записати
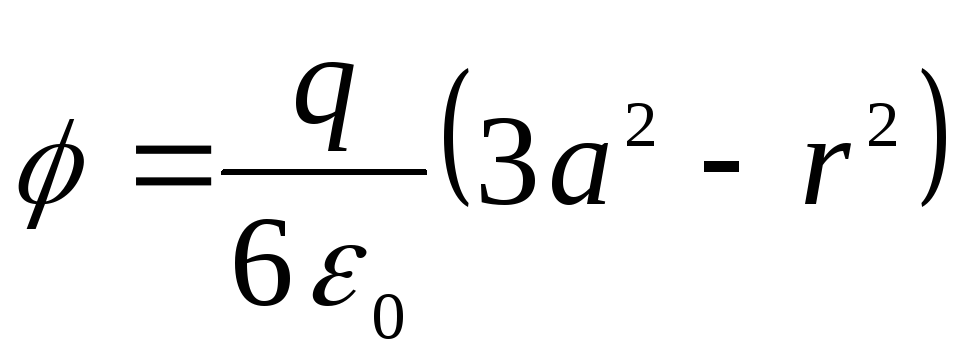 ,
,
тобто. ми дійшли тієї ж формулі, як і під час вирішення завдання шляхом інтегрування рівняння Пуассона.
1.7.6. Потенціал результуючого поля у точці A
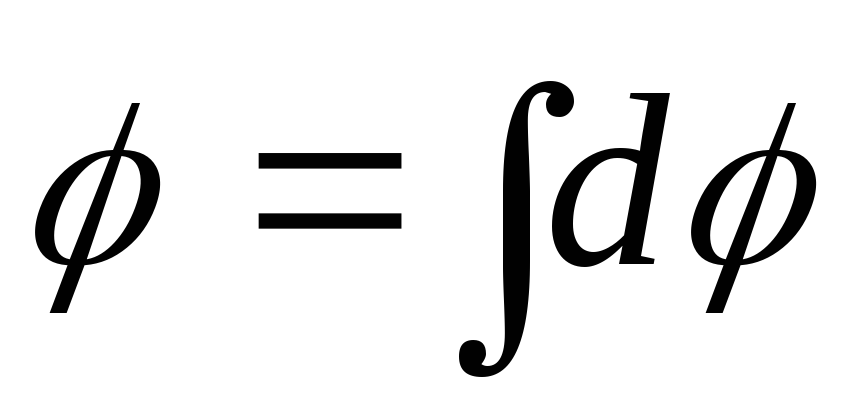 ,
,
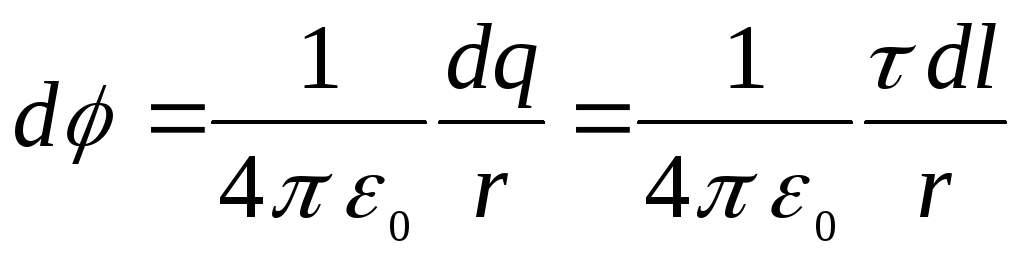
є потенціал поля, створеного зарядом 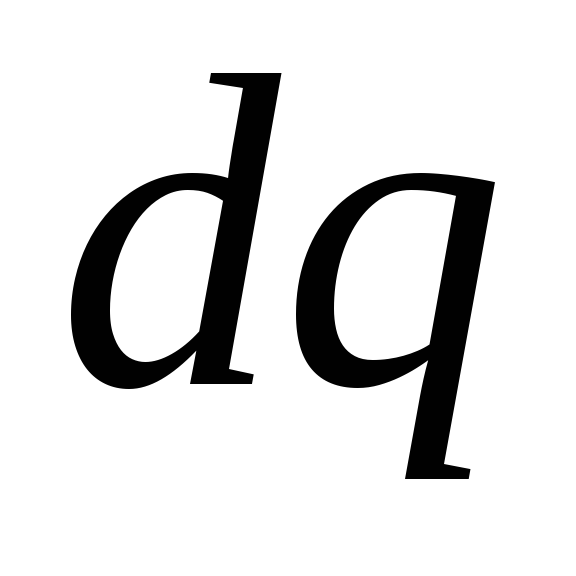 елемента кільця
елемента кільця  .
.
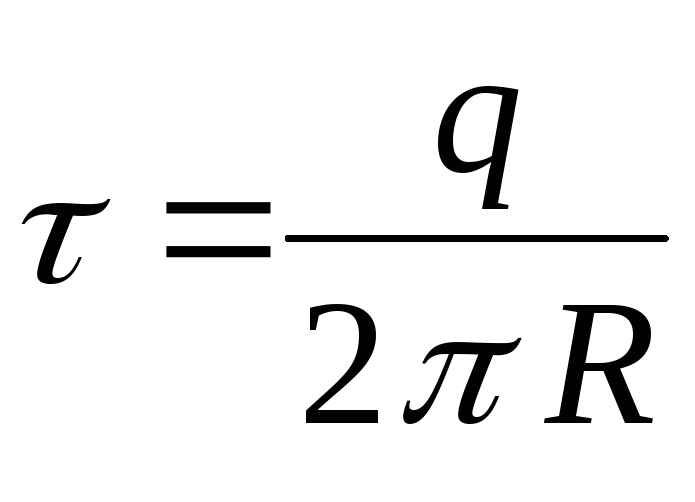
є лінійна щільність заряду, r – відстань від елемента  до вказаної точки. З двох останніх формул маємо
до вказаної точки. З двох останніх формул маємо
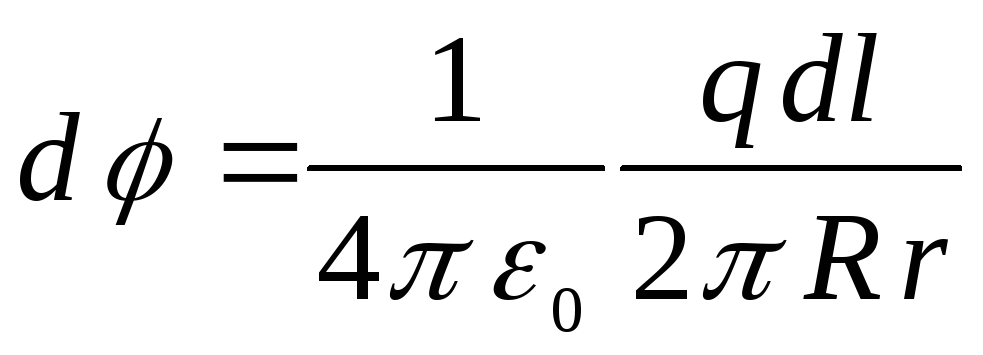 .
.
Результуючий потенціал
З геометричних міркувань випливає, що
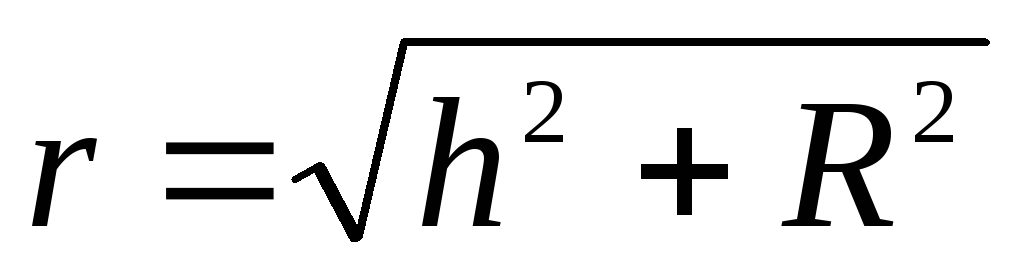 .
.
Отже,
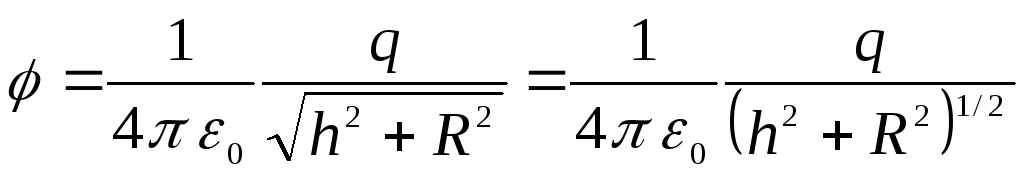 .
.
Напруженість поля
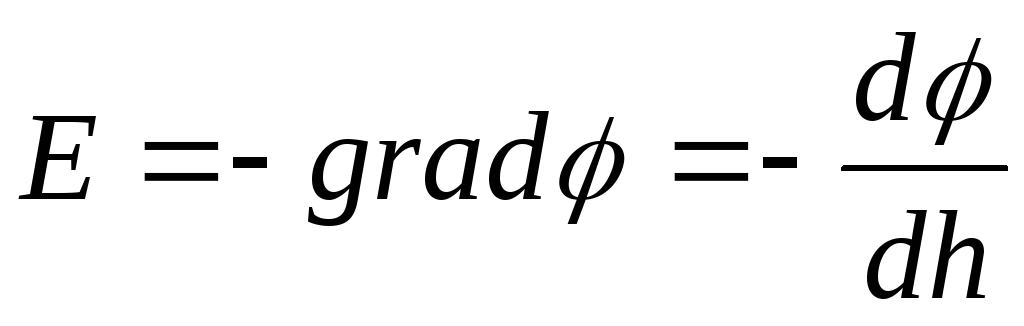 .
.
Аналіз виразів 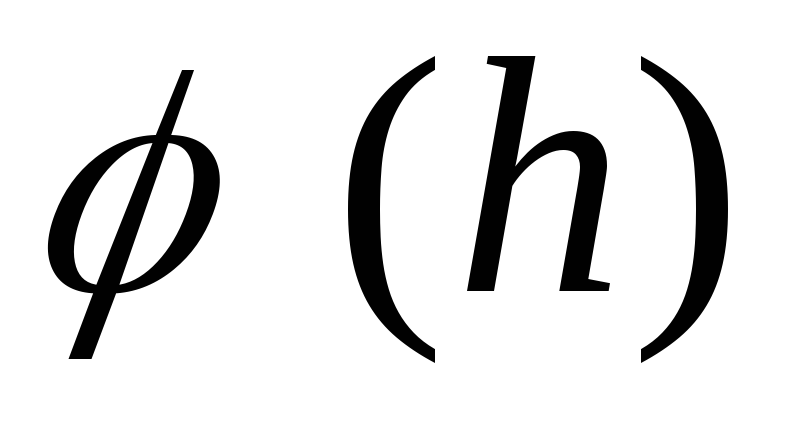 і
і ![]() показує, що в центрі кільця (
показує, що в центрі кільця ( 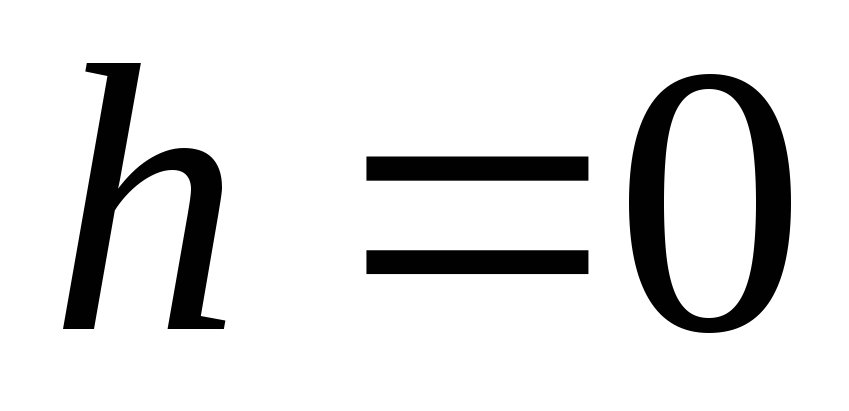 ) потенціал має максимальне значення, а напруженість поля перетворюється на нуль.
) потенціал має максимальне значення, а напруженість поля перетворюється на нуль.
При 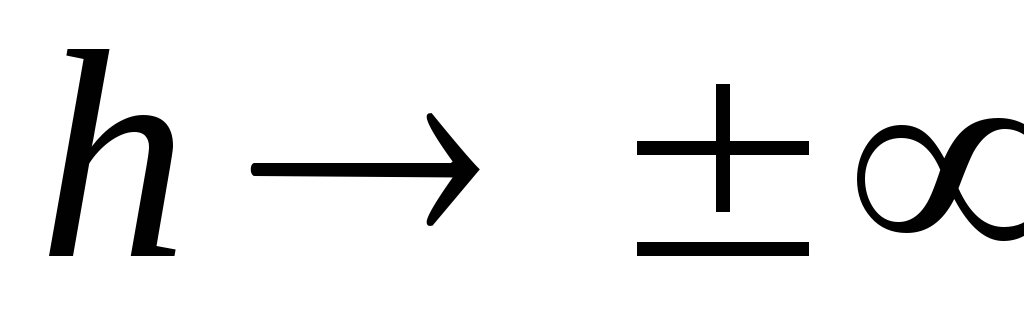 і потенціал, і напруженість прагнуть нуля.
і потенціал, і напруженість прагнуть нуля.
При 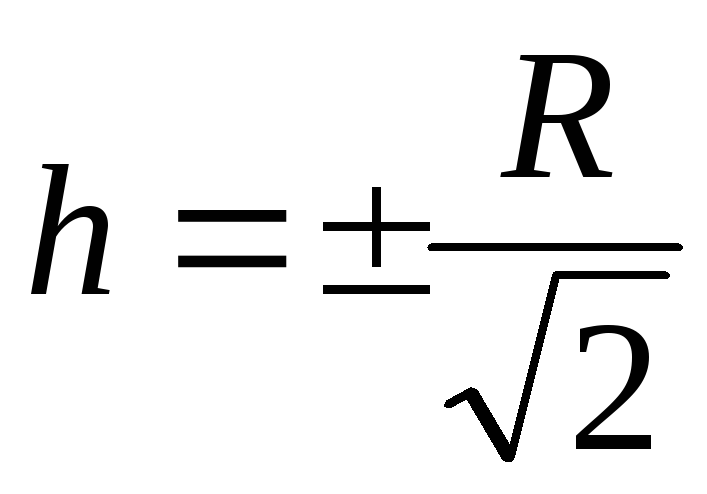 похідна
похідна 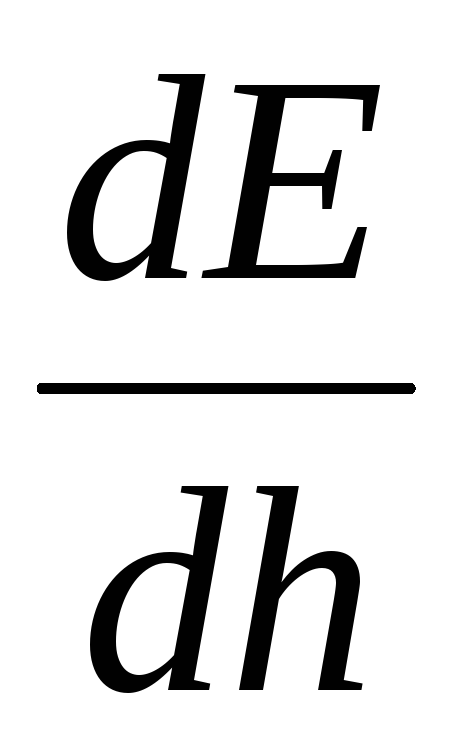 перетворюється на нуль, отже, у цій точці напруженість поля максимальна, але в графіці
перетворюється на нуль, отже, у цій точці напруженість поля максимальна, але в графіці 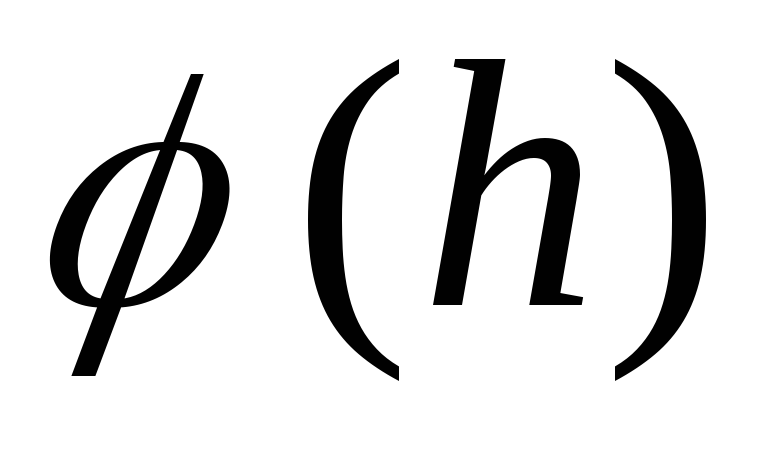 (див. рис. ____) буде точка перегину. Графік
(див. рис. ____) буде точка перегину. Графік ![]() розташований у 1-й та 3-й чвертях, тобто.
розташований у 1-й та 3-й чвертях, тобто. 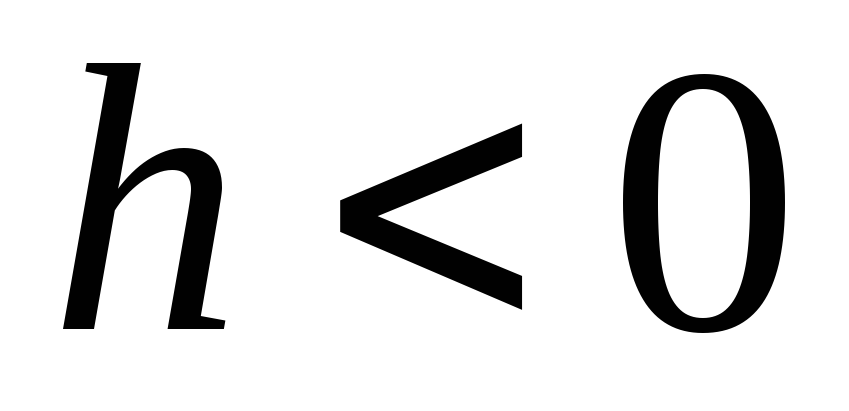 ,
,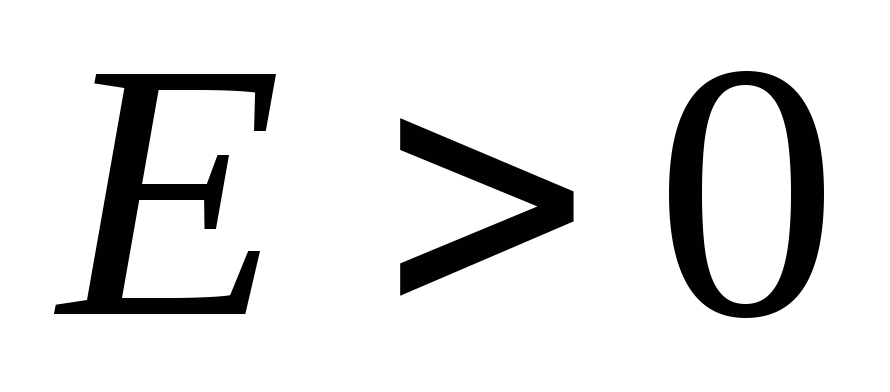 . Це означає, що при переході через центр кільця (
. Це означає, що при переході через центр кільця ( 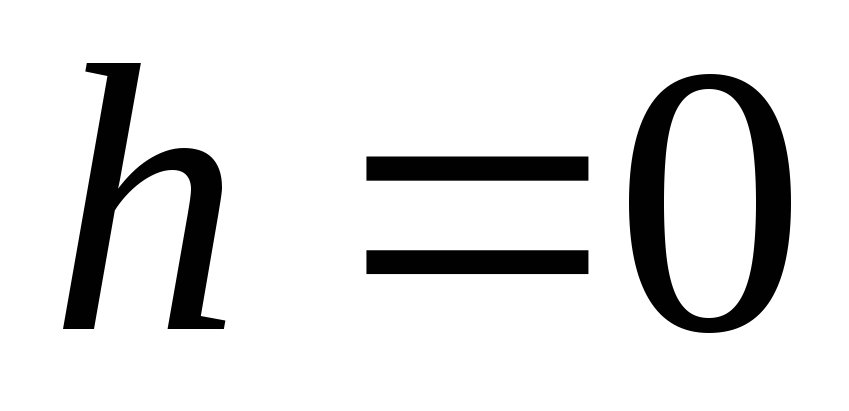 ) вектор
) вектор  змінює свій напрямок на протилежний.
змінює свій напрямок на протилежний.
Графік 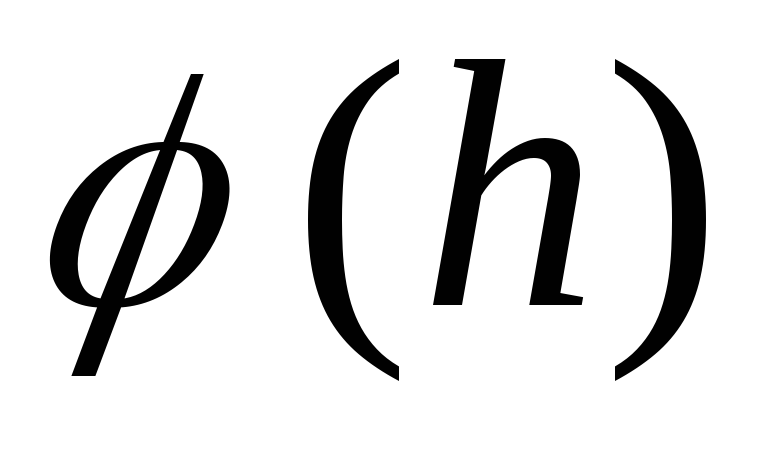 розташований у 1-й та 2-й чвертях, тобто. з обох боків від кільця в точках, що лежать на його осі, потенціал позитивний.
розташований у 1-й та 2-й чвертях, тобто. з обох боків від кільця в точках, що лежать на його осі, потенціал позитивний.
На прикладі вирішення цього завдання можна переконатися, що при зміні початку відліку потенціалу різниця потенціалів між двома будь-якими точками не змінюється. Не змінюється весь характер залежності потенціалу від відстані. Наприклад, якщо вибрати початок відліку у центрі кільця, тобто. якщо припустити, що 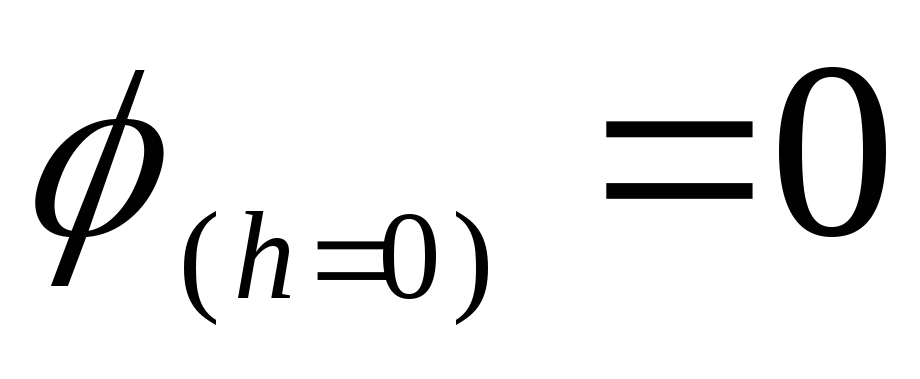 , то потенціал будь-якої точки, що лежить на осі кільця, дорівнює
, то потенціал будь-якої точки, що лежить на осі кільця, дорівнює
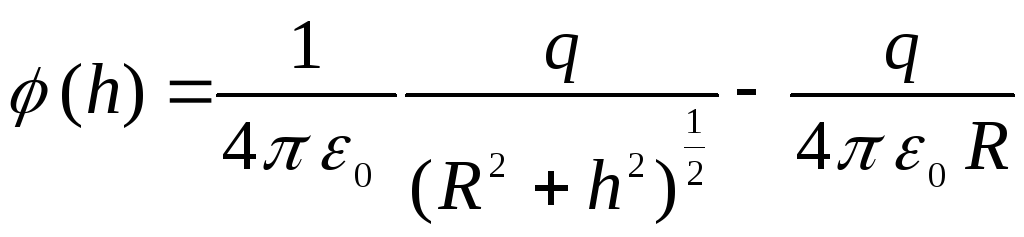 .
.
Ця формула може бути легко отримана на основі принципу суперпозиції.
Якщо початок відліку потенціалу вибрано в центрі кільця, то потенціал поля, створеного елементарним зарядом 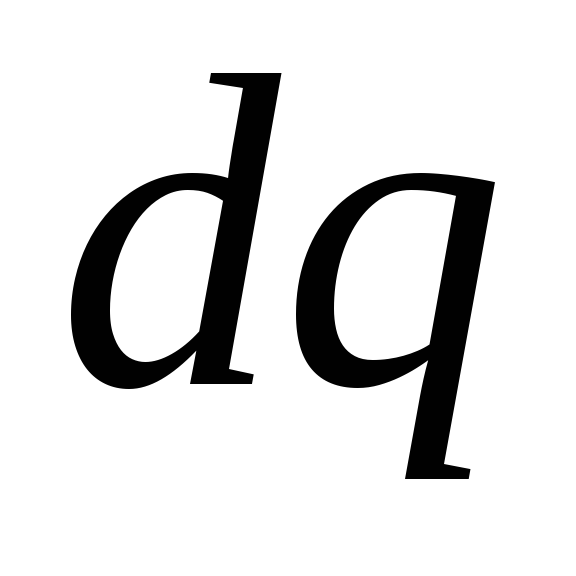 у точці A, можна подати у вигляді
у точці A, можна подати у вигляді
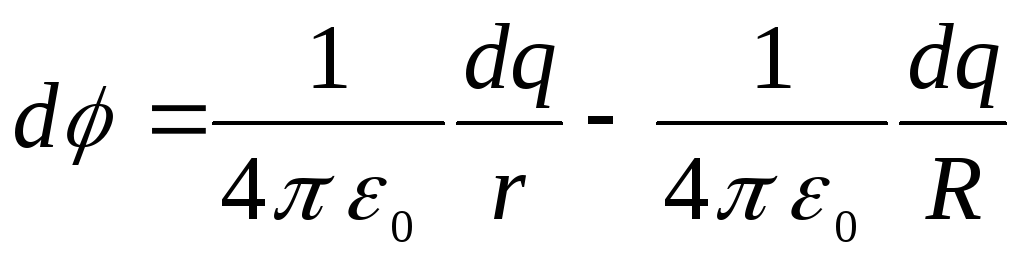 .
.
Інтегруючи цей вираз по всьому кільцю, отримаємо формулу
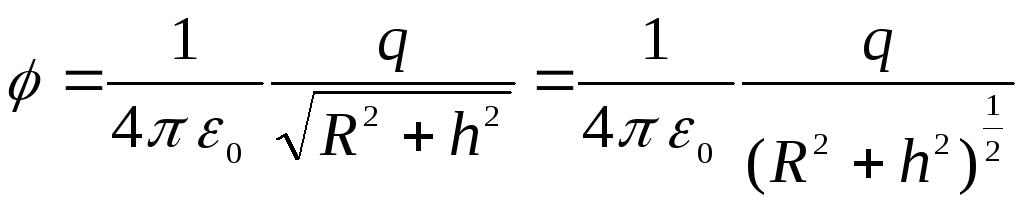 .
.
Графік залежності 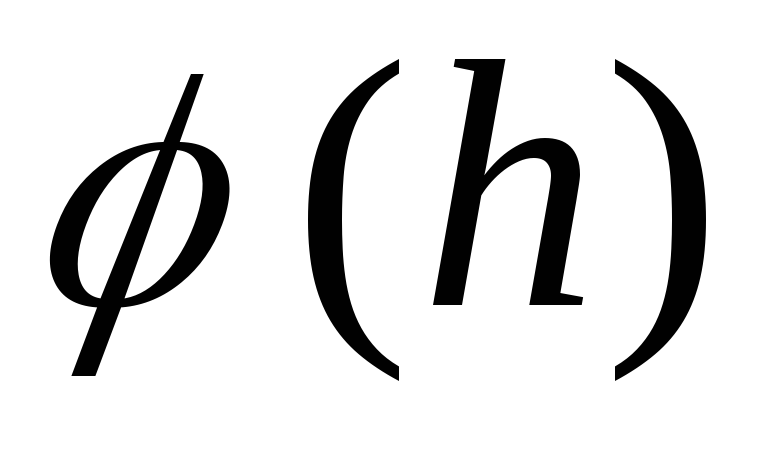 , не змінюючи свого характеру, зміщується вниз паралельно самому собі на величину
, не змінюючи свого характеру, зміщується вниз паралельно самому собі на величину 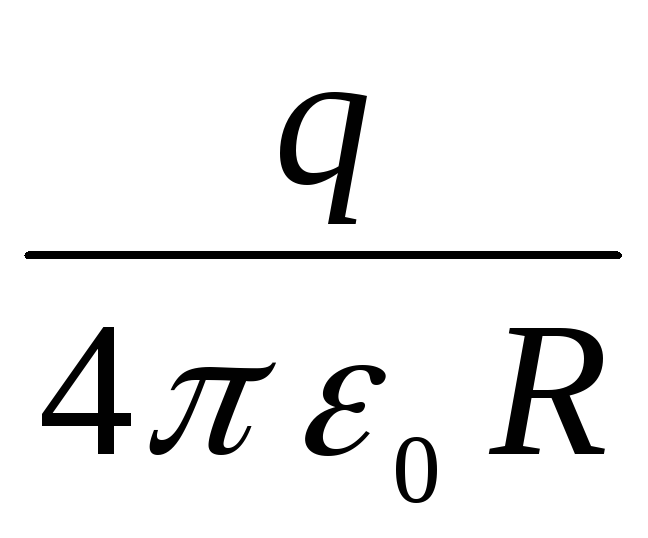 (Пунктирна лінія на малюнку _____2). При
(Пунктирна лінія на малюнку _____2). При 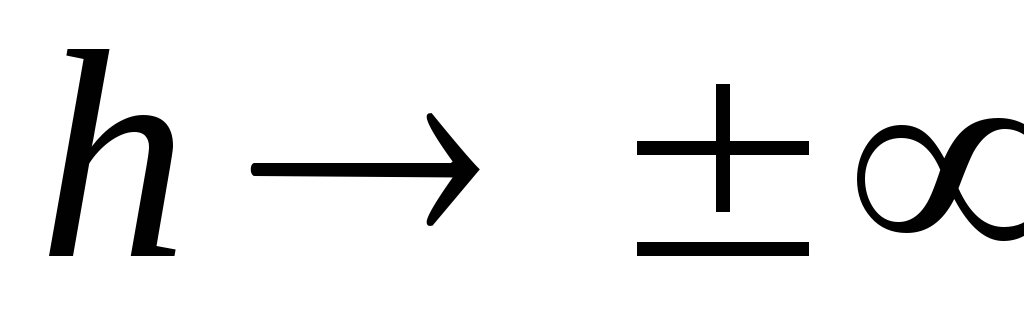 потенціал прагне значення
потенціал прагне значення 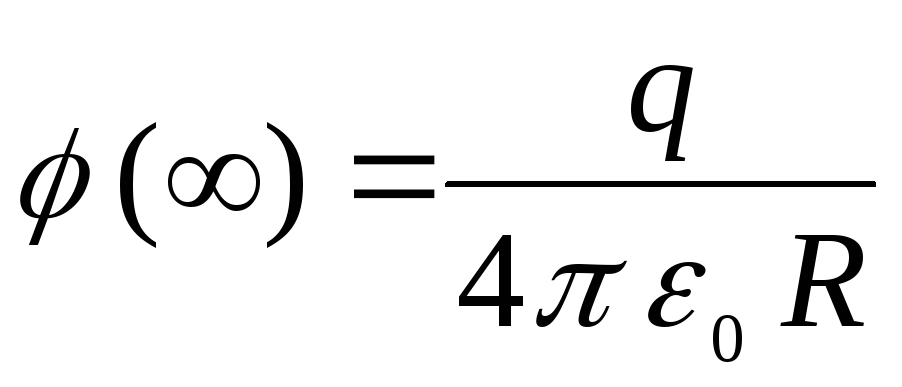 .
.
7.7. Потенціал чисельно дорівнює роботі, Здійснюваної силами електричного поля при переміщенні одиничного позитивного заряду з цієї точки поля (у нашому випадку, з поверхні внутрішньої сфери) в безкінечність.
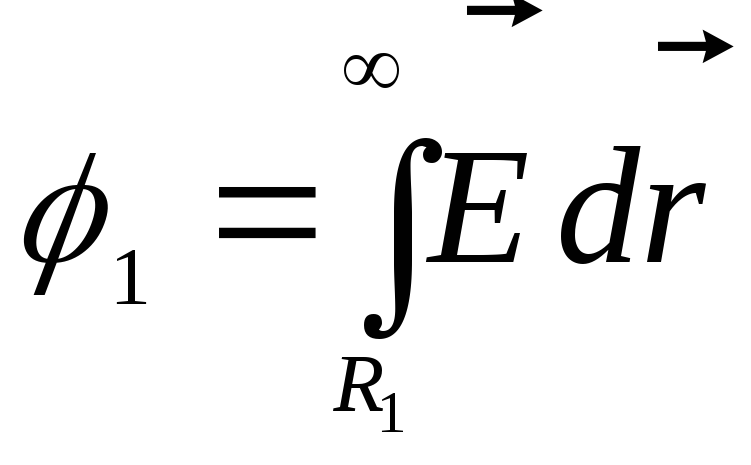 ,
,
де  – результуюча напруженість поля у всіх точках інтервалу інтегрування.
– результуюча напруженість поля у всіх точках інтервалу інтегрування.
В інтервалі 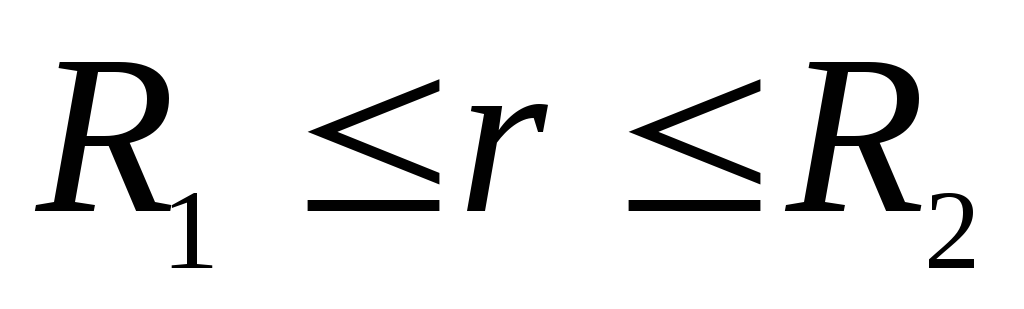 поле створюється лише зарядом внутрішньої сфери. Вектор
поле створюється лише зарядом внутрішньої сфери. Вектор  незалежно від величини та знаку заряду
незалежно від величини та знаку заряду 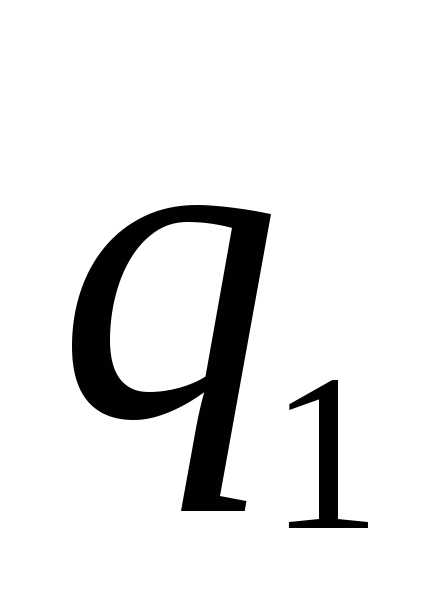 , спрямований по радіусу від центру При переміщенні одиничного позитивного заряду від
, спрямований по радіусу від центру При переміщенні одиничного позитивного заряду від  до
до 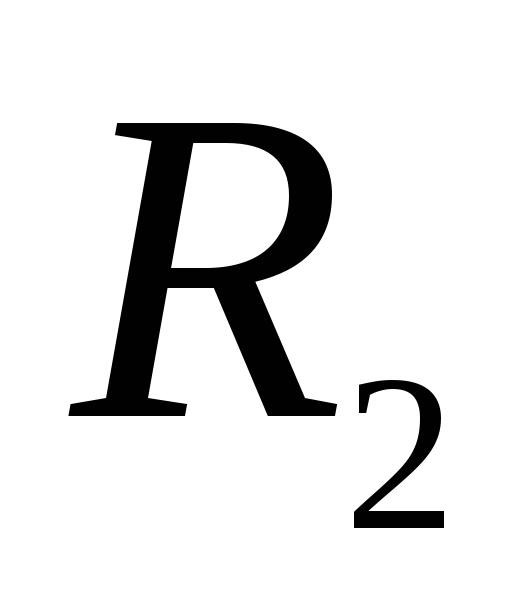 сили поля виконують позитивну роботу. При
сили поля виконують позитивну роботу. При 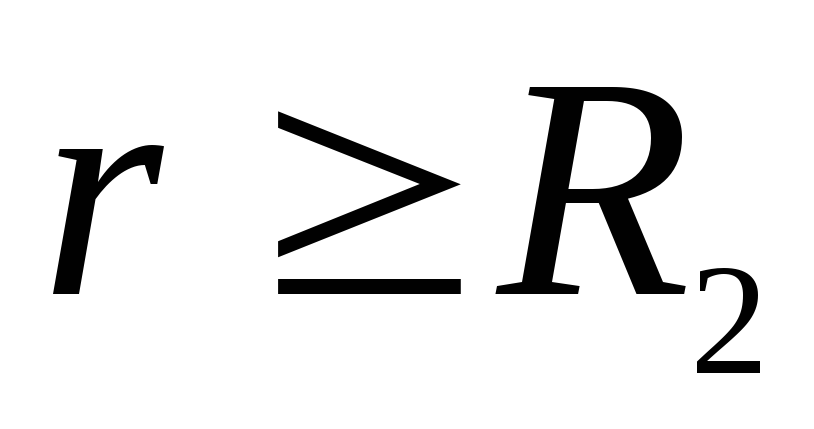 , тобто. за межами другої сфери робота сил поля негативна і, отже, вектор
, тобто. за межами другої сфери робота сил поля негативна і, отже, вектор  спрямований за радіусом до центру сфери. У точках
спрямований за радіусом до центру сфери. У точках 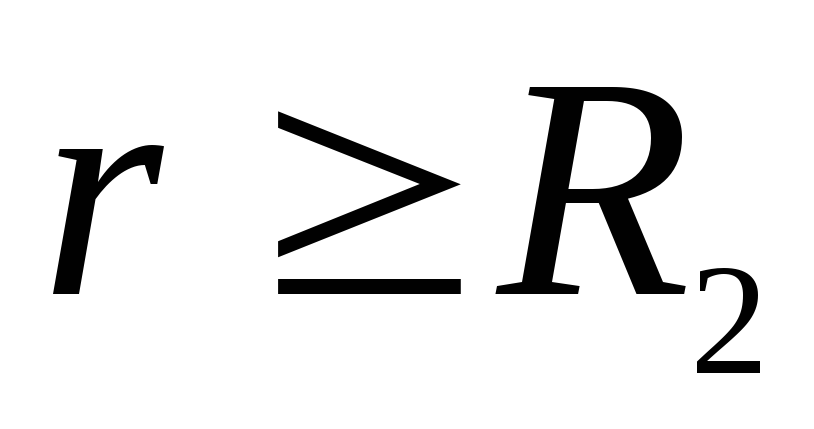 поле визначається сумою алгебри зарядів на обох сферах. Заряд
поле визначається сумою алгебри зарядів на обох сферах. Заряд 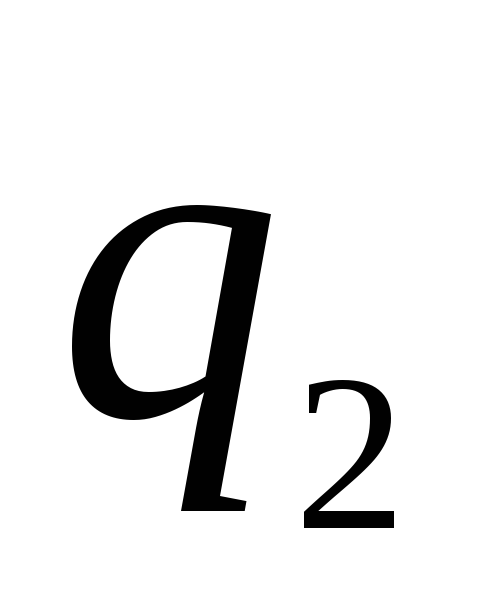 має бути негативним і за величиною має бути більше заряду
має бути негативним і за величиною має бути більше заряду 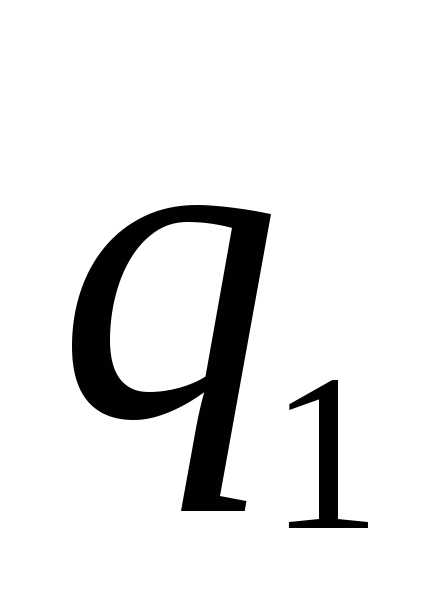 . Оскільки вектори
. Оскільки вектори  і
і 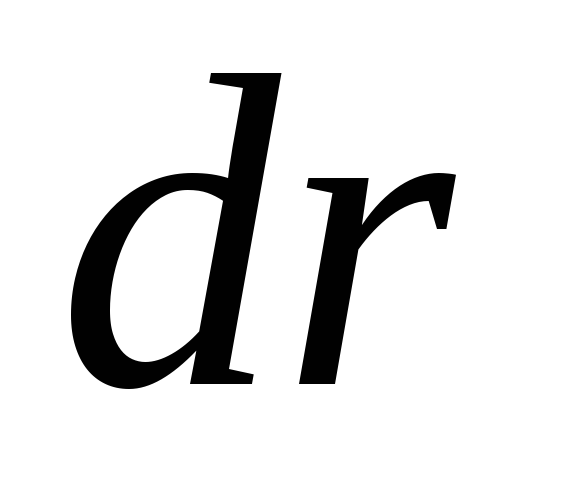 колінеарні (або антиколінеарні при
колінеарні (або антиколінеарні при 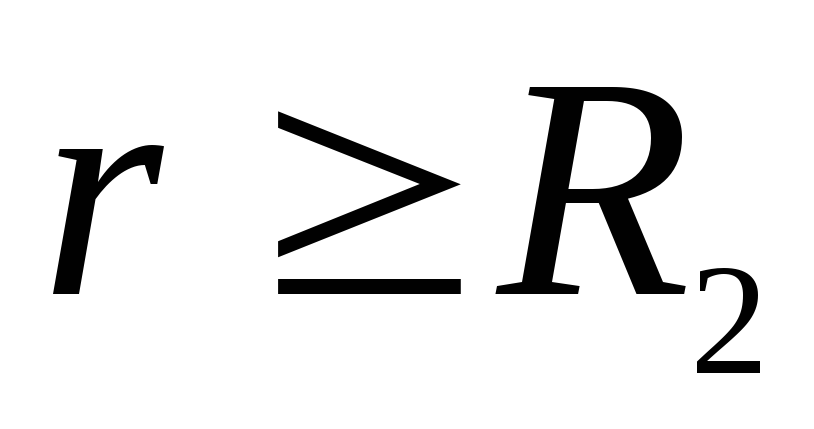 ), то скалярний твір
), то скалярний твір ![]() можна замінити твором
можна замінити твором 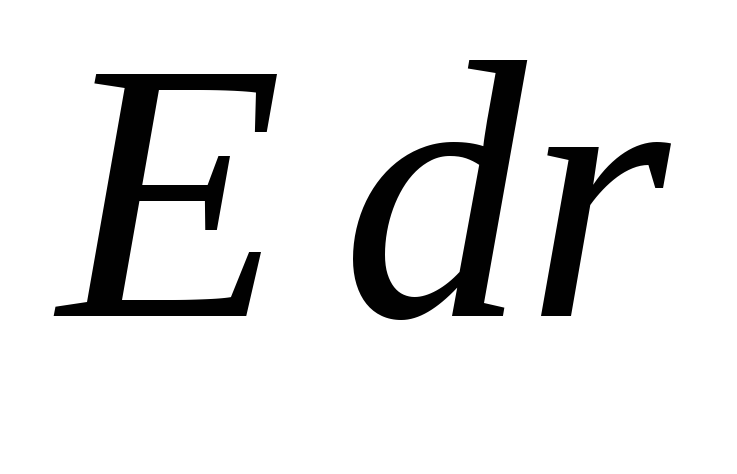 (у разі, коли ці два вектори спрямовані протилежно, напруженість поля має вважатися негативною). У формулі
(у разі, коли ці два вектори спрямовані протилежно, напруженість поля має вважатися негативною). У формулі 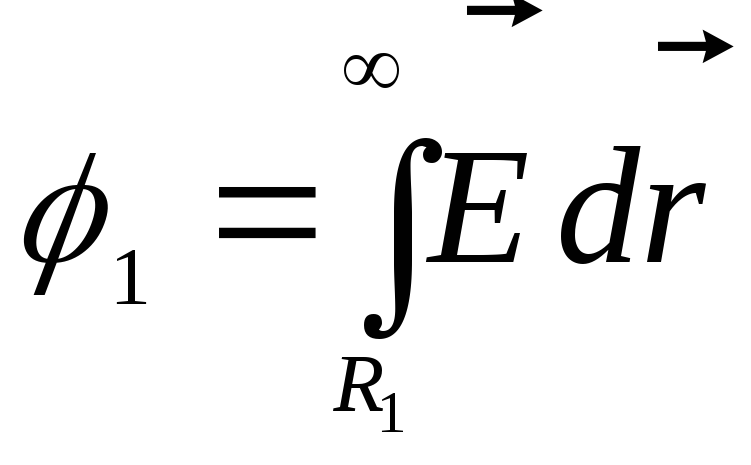 підінтегральна функція
підінтегральна функція 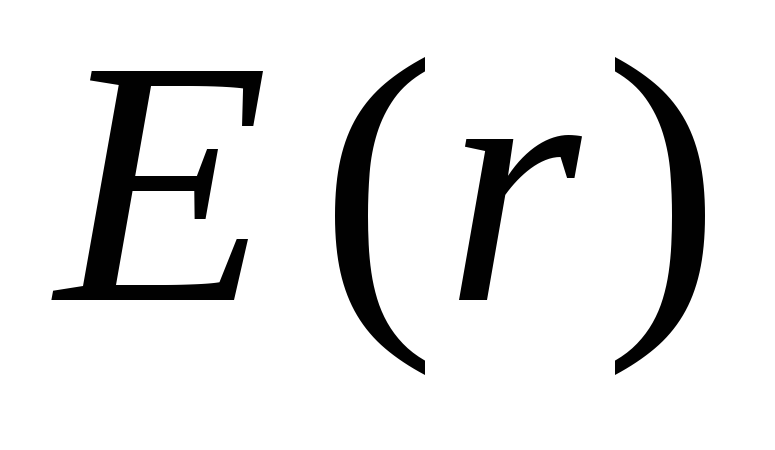 терпить розрив у точці
терпить розрив у точці 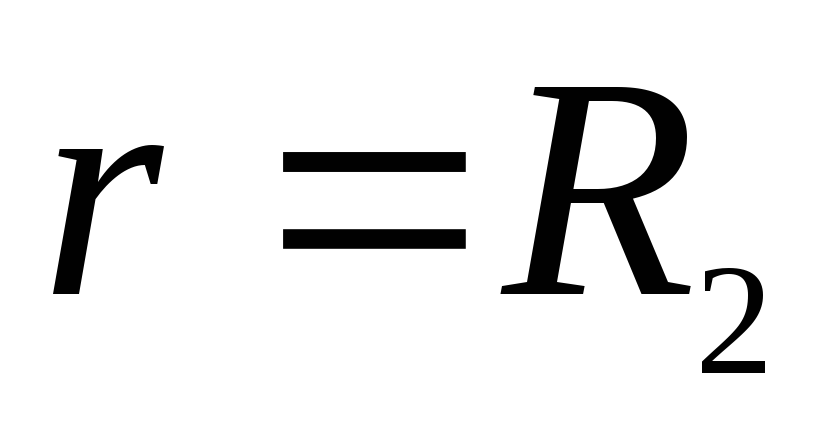 . Тому інтеграл потрібно розбити на два інтеграли в межах від
. Тому інтеграл потрібно розбити на два інтеграли в межах від  до
до 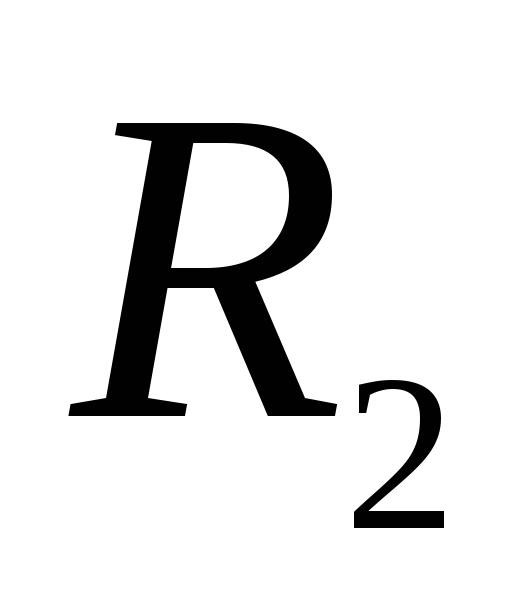 і от
і от 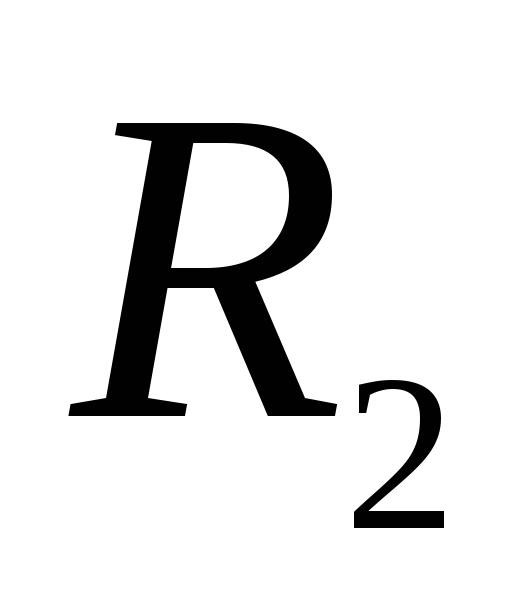 до
до  :
:
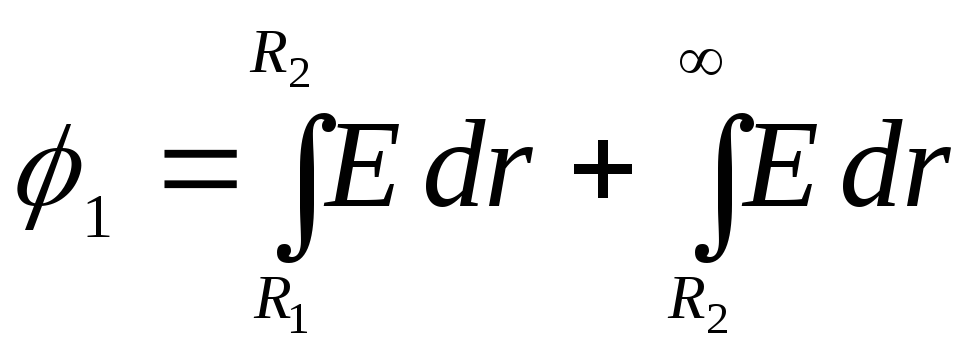 .
.
При 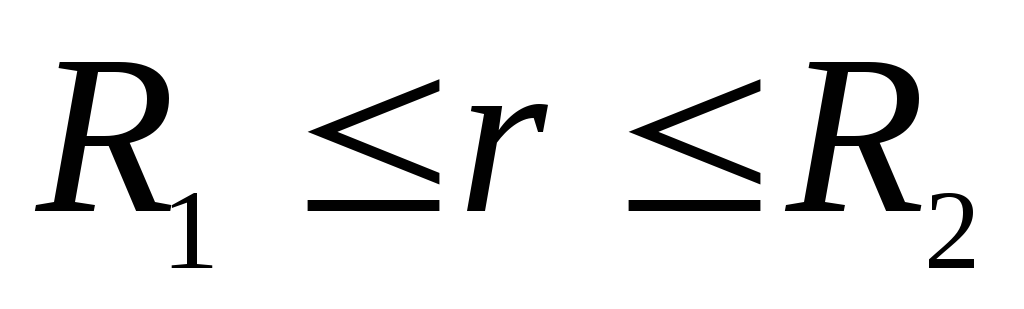 напруженість
напруженість
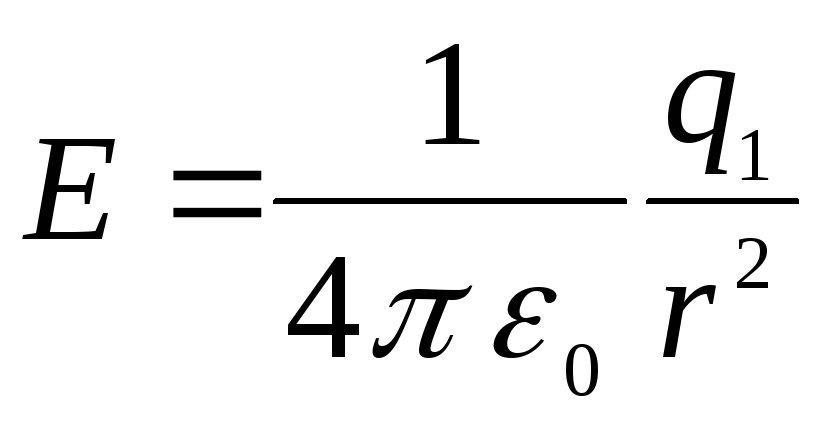 ,
,
а при 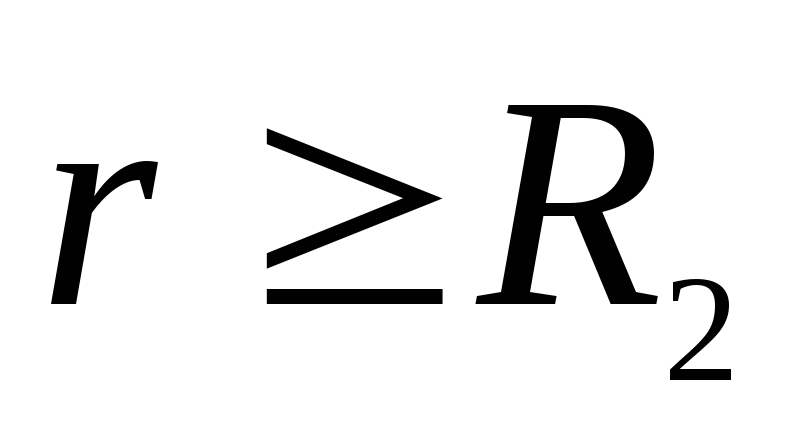
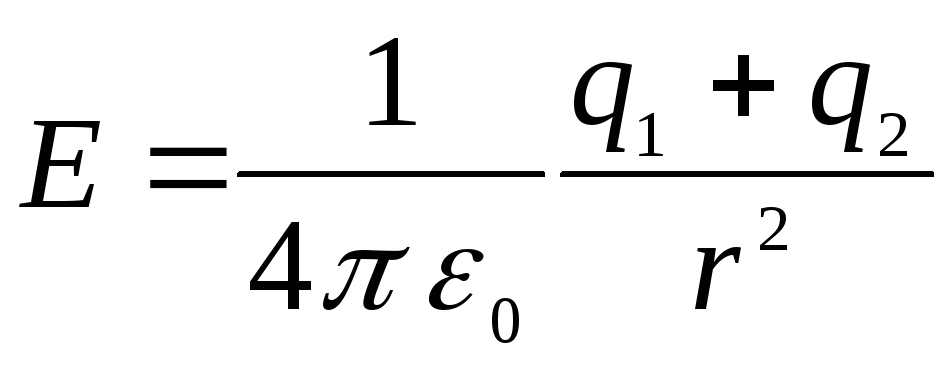 .
.
Підставивши ці висловлювання у відповідні інтеграли, отримаємо
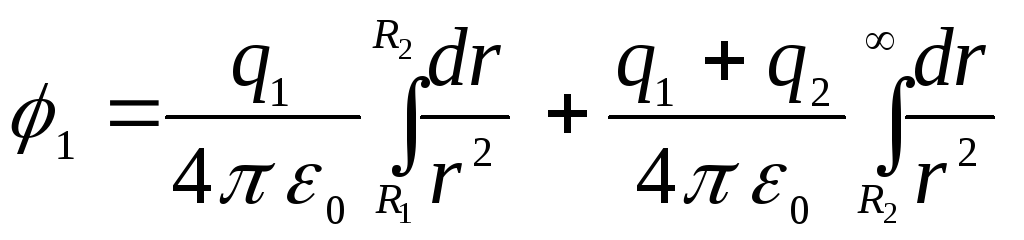 .
.
Інтегруючи та наводячи подібні члени, отримаємо
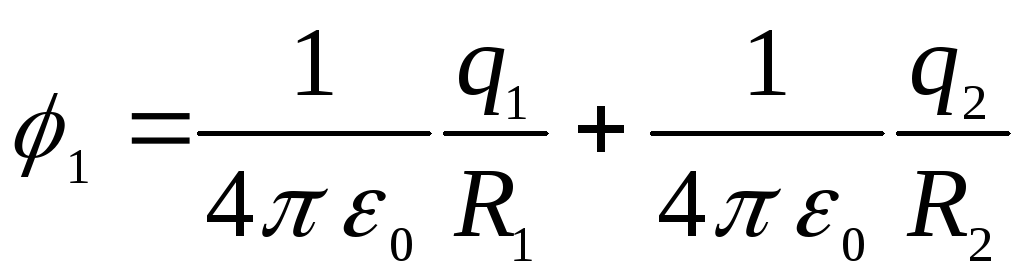 .
.
Оскільки за умовою завдання 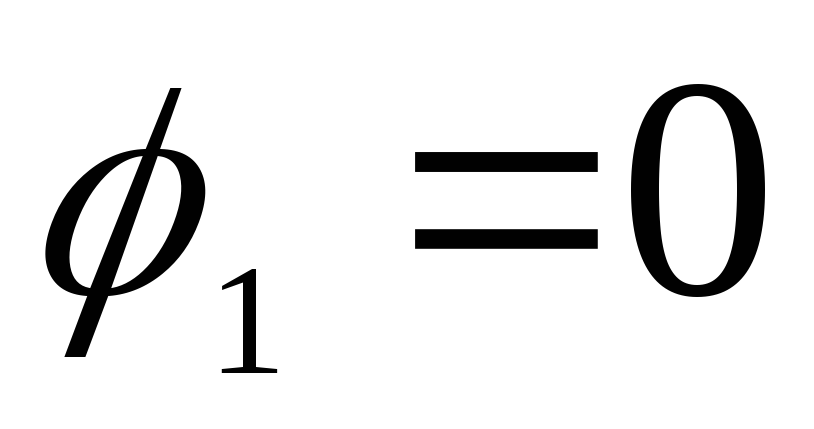 , то
, то
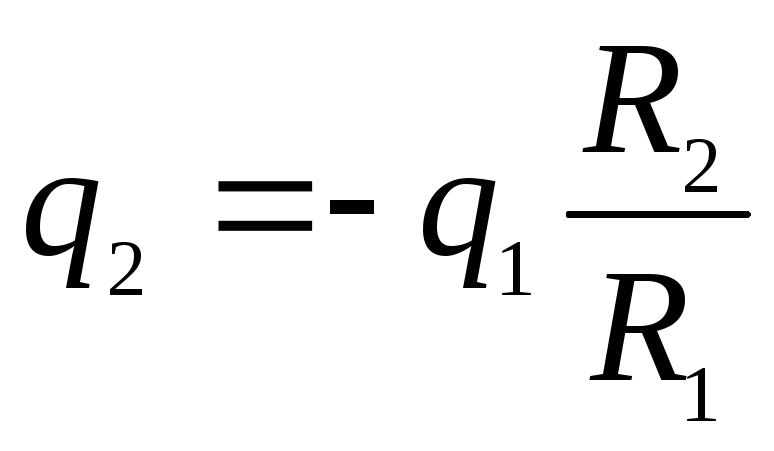 .
.
Графік залежності 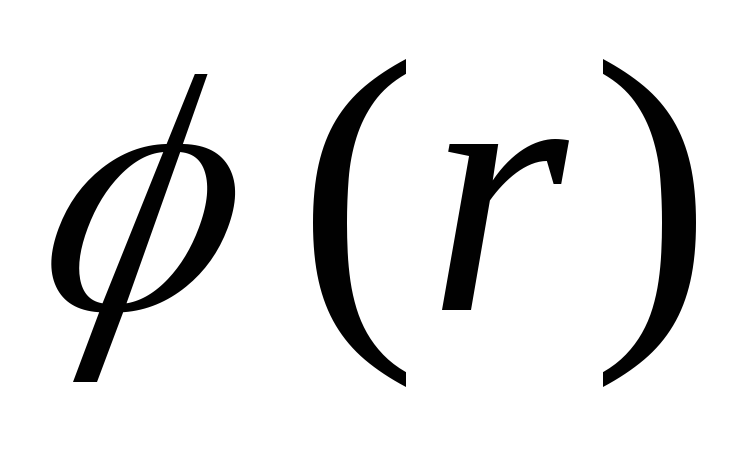 зображено малюнку ____.
зображено малюнку ____.
Проаналізуємо отриманий графік.
Відповідно до умови завдання, за заданого значення 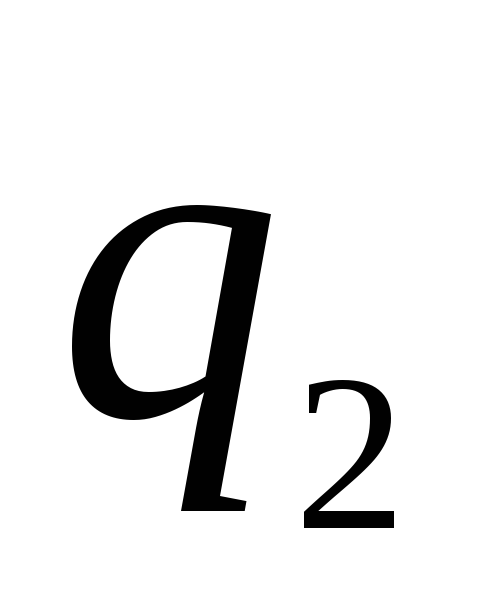 потенціал на поверхні внутрішньої сфери
потенціал на поверхні внутрішньої сфери 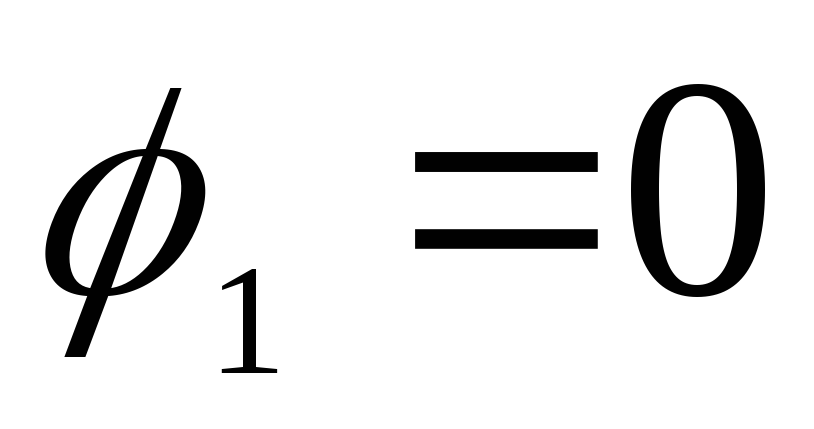 . При
. При 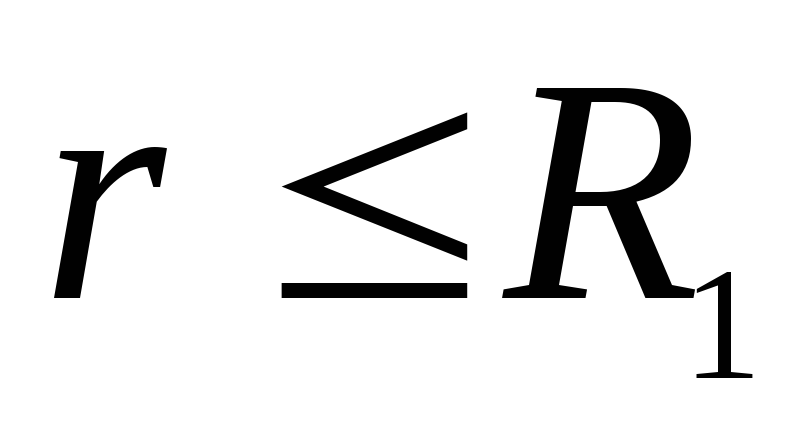 потенціал постійний і дорівнює потенціалу на поверхні, отже, графіком на ділянці від
потенціал постійний і дорівнює потенціалу на поверхні, отже, графіком на ділянці від 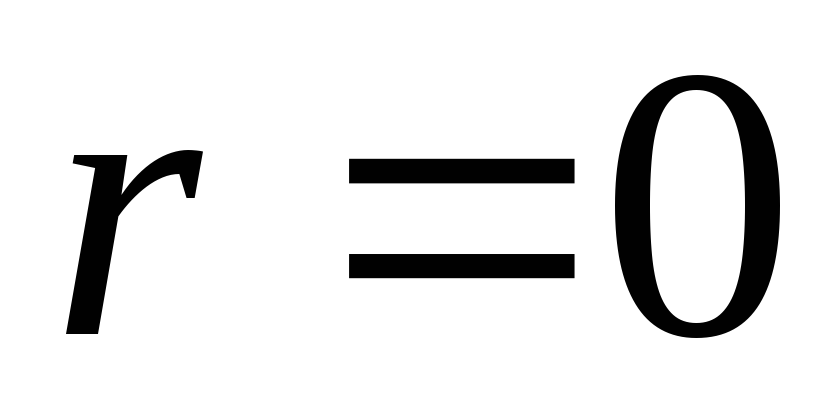 до
до 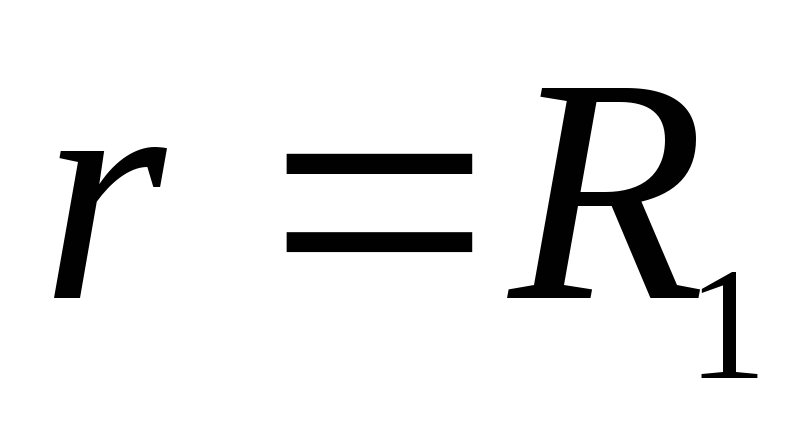 є пряма лінія, що збігається з віссю абсцис. При
є пряма лінія, що збігається з віссю абсцис. При 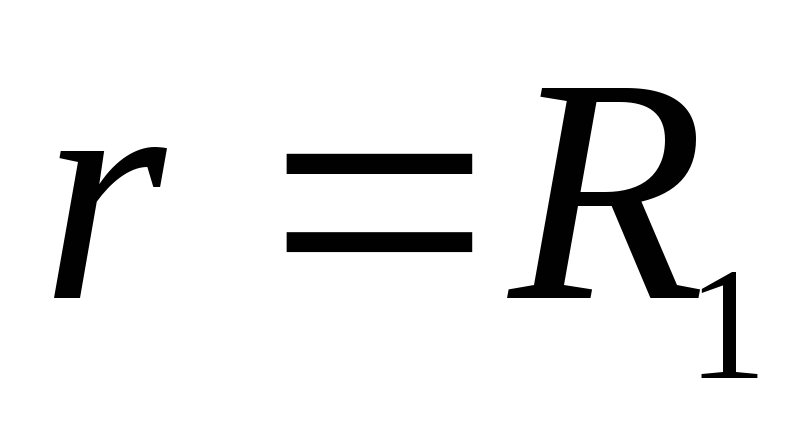 вектор
вектор  терпить розрив. Так як
терпить розрив. Так як 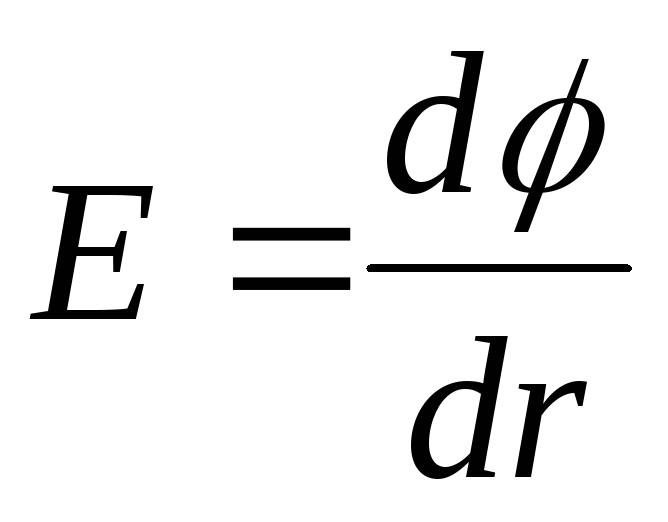 , то на графіку точка
, то на графіку точка 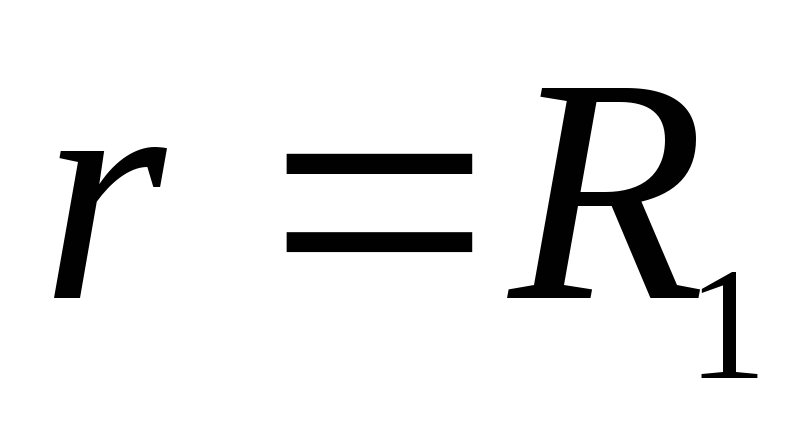 (так само, як і точка
(так само, як і точка 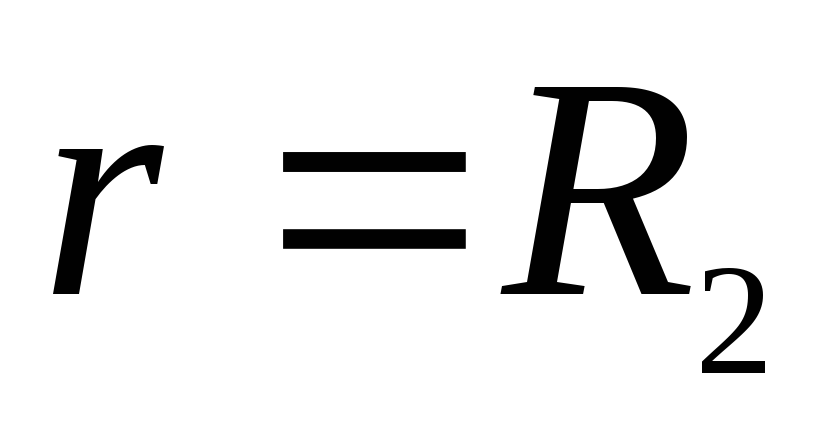 ) представляють спеціальні точки. На ділянці
) представляють спеціальні точки. На ділянці 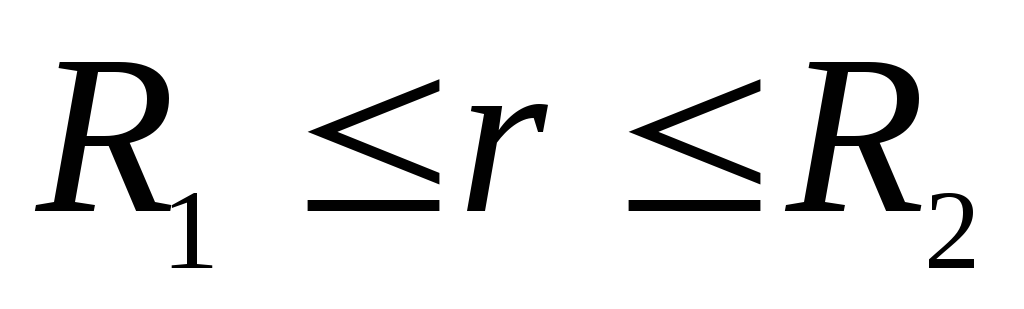 вектор
вектор  спрямований по радіусу – вектору
спрямований по радіусу – вектору 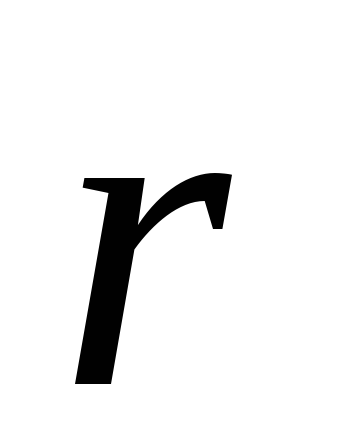 . Тому, в міру віддалення від поверхні внутрішньої сфери потенціал зменшується до деякого значення
. Тому, в міру віддалення від поверхні внутрішньої сфери потенціал зменшується до деякого значення 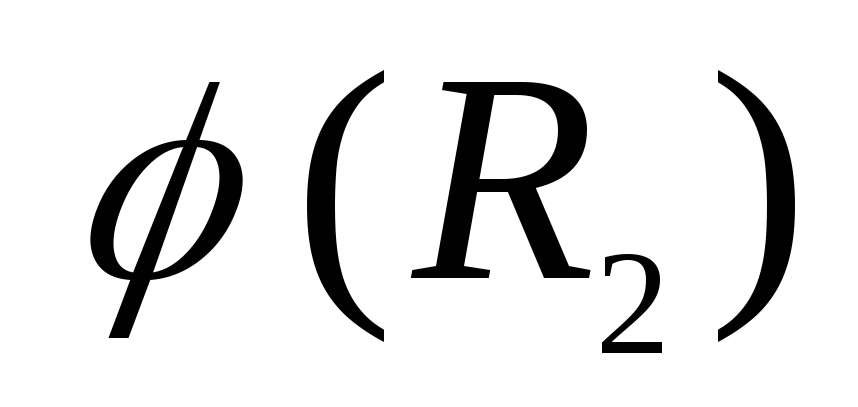 . На ділянці
. На ділянці 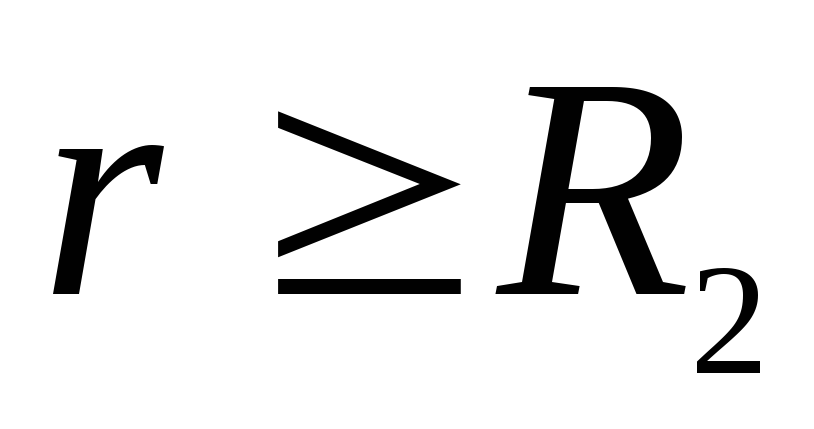 вектор
вектор  спрямований назустріч радіусу.
спрямований назустріч радіусу. 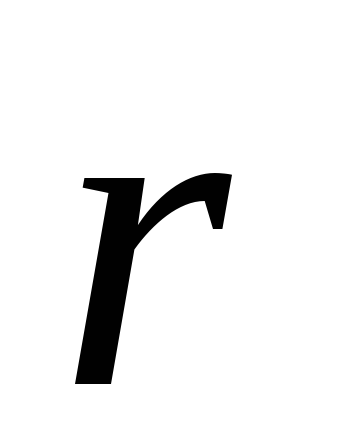 , тому, в міру віддалення від поверхні зовнішньої сфери потенціал зростає, і при
, тому, в міру віддалення від поверхні зовнішньої сфери потенціал зростає, і при 
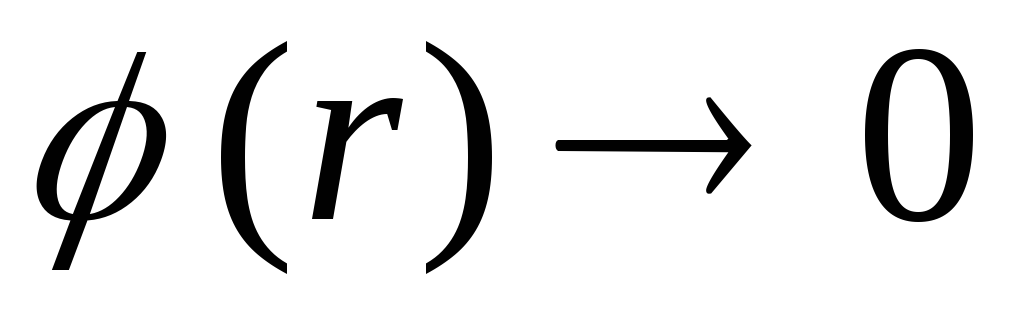 . Незважаючи на те, що в точках
. Незважаючи на те, що в точках 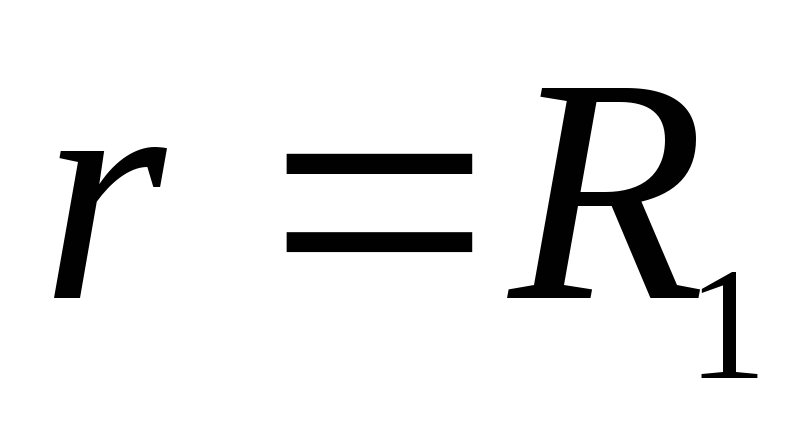 і
і 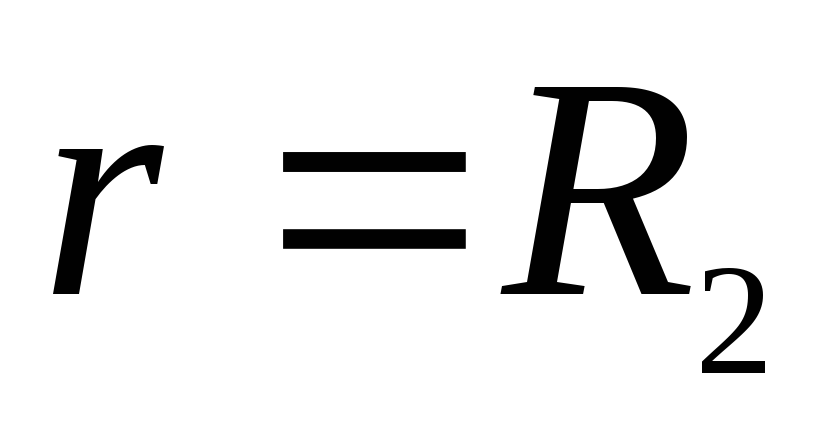 вектор
вектор  терпить розрив, функція
терпить розрив, функція 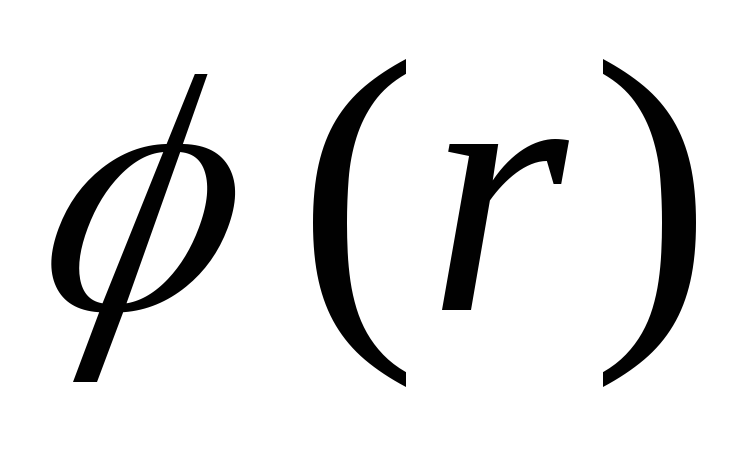 є безперервною.
є безперервною.
Серед шкільних завдань з фізики особняком стоять ті, які пов'язані з концентричними сферами, що проводять. Ці сфери може бути заряджені, заземлені, можуть бути у полі зовнішніх зарядів тощо. буд., варіацій багато. У шкільному курсіФізики ці завдання є одними з найскладніших. Не в останню чергу, звичайно, нерозуміння цього матеріалу пов'язане з нездатністю вчителів пояснити його грамотно та доступно. Отже, спробуємо розібратися, що це за сфери, що проводять, і з чим їх їдять.
Потенціал внутрішньої сфери φ 2 визначається відомим співвідношенням:
![]()
Тоді загальний потенціал φ in на поверхні внутрішньої сфери дорівнює:
Потенціал на поверхні зовнішньої сфери також складається із двох потенціалів: внутрішньої сфери φ’ 1 і власне зовнішньої сфери φ’ 2 .
Потенціал внутрішньої сфери φ’ 1 на відстані Rвід її центру визначається відомим співвідношенням:
![]()
Формула, що визначає потенціал зовнішньої сфери φ’ 2 на її поверхні, також добре відома:
![]()
Тоді загальний потенціал на поверхні зовнішньої сфери дорівнює:
![]()
Рішення.До з'єднання сфер провідником заряд першої дорівнював:
Після з'єднання частина заряду із внутрішньої сфери перетекла на зовнішню. Струм припинився в той момент, коли потенціал кулі став рівний потенціалу зовнішньої оболонки. Зручніше тому шукати не потенціал кулі, а рівний потенціал зовнішньої оболонки. Відповідно до результатів, отриманих у попередній задачі, цей потенціал визначається виразом:
![]()
де q 1 і q 2 - заряди кулі та зовнішньої оболонки після з'єднання їх провідником відповідно. За законом збереження заряду q = q 1 + q 2 . Після нескладних перетворень отримуємо:
![]()
Почнемо з малюнка до розв'язання задачі:
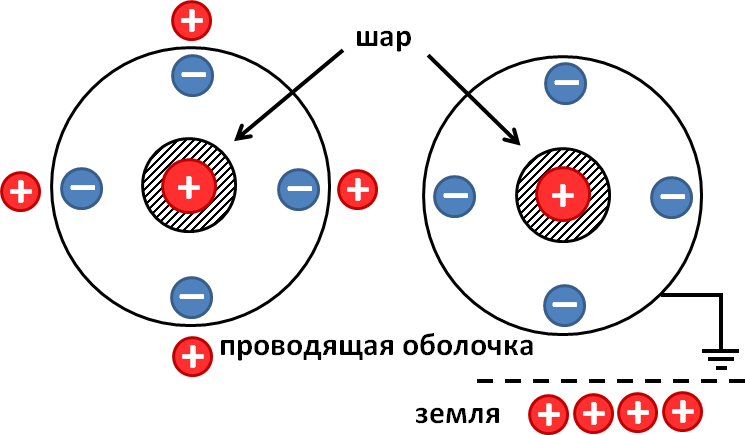
Після заземлення провідної оболонки весь позитивний заряд, що утворився на ній внаслідок явища електростатичної індукції, стікає на землю. На ній залишається лише негативний заряд, оскільки він притягується до позитивного заряду внутрішньої сфери.
Рішення.Знаючи потенціал кулі в початковий момент часу та її радіус, можна знайти заряд на ньому:
Внаслідок явища електростатичної індукції на зовнішній оболонці має відбутися поділ заряду. Негативний заряд перетікає на внутрішню поверхню оболонки, позитивний на зовнішню (див. малюнок). Це ж явище виникало і в попередніх завданнях, але ми не брали його до уваги. Чому? В умові завдань було зазначено, що оболонка тонка, і таке «розбігання» зарядів не призводило до скільки-небудь істотної зміни конфігурації електростатичного поля.
У цьому завданні облік даного явищаважливий, оскільки оболонку заземлюють. Після заземлення позитивний заряд із оболонки стіче на землю, залишиться лише негативний q 2 , оскільки він притягується до позитивного заряду q 1 внутрішньої сфери. Потенціал заземленої оболонки дорівнюватиме потенціалу землі, тобто нулю. У зв'язку з цим і відповідно до результату, отриманого при вирішенні першого завдання, отримуємо рівність:
Використовуючи вираз для розрахунку потенціалу внутрішньої сфери подібної системи, отриманий у першому завданні, знаходимо остаточно необхідний потенціал кулі:
![]()
![]()
Досвід показує, що мало хто розуміє рішення цих завдань у всіх деталях з першого разу. Зазвичай доводиться довго і наполегливо роз'яснювати учням всі ті дрібниці, без усвідомлення яких рішення зводиться до порожніх перетворень буквених виразів з одержання наведеної наприкінці підручника відповіді. Зрозуміти фізичну сутність цих завдань та навчитися застосовувати отримані знання у майбутньому не просто. Однак у цьому полягає основна методична цінність цієї теми у шкільному курсі фізики. Кращим помічником у її вивченні неодмінно стане професійний репетитор, грамотний наставник, який зможе придумати зрозуміле саме вам пояснення і відповість на всі запитання. До речі, якщо вони є, ви можете задати їх нижче в коментарях.
Сергій Валерійович