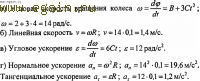- leņķiskais paātrinājums, kas izteikts apgriezienos, apgriezienu skaitu var attēlot kā n k = n 0 + e"t un tad

http://pandia.ru/text/80/153/images/image553.gif" width="201" height="37 src=">

kas atbilst

n1 = 2 x 60 = 120 apgr./min.

Tagad mēs atrodam pie šāda spararata griešanās ātruma punktu ātrumu uz tā loka:

http://pandia.ru/text/80/153/images/image555.gif" width="236" height="20 src=">

45. uzdevums. Vārpsta, kas rotē vienmērīgi paātrinātā stāvoklī no miera stāvokļa, pirmajās 12 sekundēs veic 95,5 apgriezienus. Ar kādu leņķisko paātrinājumu vārpsta griežas un kādu leņķisko ātrumu tā iegūst?

Risinājums.

1. Leņķiskā nobīde laika gaitā t\u003d 12 ar vienmērīgi paātrinātu kustību ir

http://pandia.ru/text/80/153/images/image557.gif" width="197" height="39 src=">

3. Līdz 12. sekundes beigām vārpsta iegūst leņķisko ātrumu:

http://pandia.ru/text/80/153/images/image559.gif" width="180" height="37 src=">

46. ​​uzdevums. Ritenis, kas griežas ar frekvenci 1500 apgr./min, bremzējot, sāk vienmērīgi griezties un apstājas pēc 30 sekundēm. Nosakiet riteņa leņķisko paātrinājumu un apgriezienu skaitu no bremzēšanas sākuma līdz apturēšanai.

Risinājums.

1. Izsakiet sākotnējo leņķisko ātrumu rad/s:

http://pandia.ru/text/80/153/images/image561.gif" width="208" height="37 src=">

2. Definējiet apgriezienu skaitu formā

http://pandia.ru/text/80/153/images/image563.gif" width="263" height="36 src=">

47. uzdevums. Vārpstas rotācija pirmajās 20 sekundēs notiek saskaņā ar vienādojumu j = 0,8t3.

Noteikt vārpstas leņķisko ātrumu 20. sekundes beigās; leņķiskais paātrinājums kustības sākumā, 10. un 20. sekundes beigās; cik apgriezienus vārpsta izdara 20 s .

Risinājums.

1. Nosakiet vārpstas apgriezienu skaitu 20s . Lai to izdarītu, vispirms atrodiet griešanās leņķi t= 20 s :

http://pandia.ru/text/80/153/images/image565.gif" width="199" height="37 src=">

2. Definējiet vienādojumu leņķiskais ātrums vārpsta:

http://pandia.ru/text/80/153/images/image567.gif" width="195" height="23 src=">

Ja izsakām šo leņķisko ātrumu apgr./min , tad

http://pandia.ru/text/80/153/images/image569.gif" width="132" height="37 src=">

5. Atrodiet leņķisko paātrinājumu kustības sākumā ( t 0= 0), 10. gada beigās ( t1= 10 s) un 20. sekundes ( t2= 20 s):

http://pandia.ru/text/80/153/images/image571.gif" width="187" height="23 src=">

5. nodaļa

§ 20. Absolūtā kustība un tās sastāvdaļas

Iepriekšējās nodaļās mēs apskatījām punkta un ķermeņa kustību attiecībā pret atskaites rāmi, kas saistīts ar Zemi, ko parasti uzskatījām par nekustīgu. Kustību attiecībā pret šo "fiksēto" koordinātu sistēmu sauc par absolūtu. Bet dažreiz ir jāņem vērā punkta kustība attiecībā pret sistēmu, kas saistīta ar ķermeni, kas pats pārvietojas attiecībā pret Zemi vai tai piestiprinātiem ķermeņiem (ēkas sienas, sliedes, automašīnas utt.). Šajā gadījumā ir ērti iedomāties punkta absolūto kustību kā sarežģītu kustību, kas sastāv no divām (vai vairākām) neatkarīgām kustībām.

Iegūstiet pilnu tekstu

Punkta kustību attiecībā pret kustīgu atskaites sistēmu sauc par relatīvu, un punkta kustību kopā ar kustīgu atskaites sistēmu attiecībā pret fiksētu atskaites sistēmu sauc par pārnēsājamu.

Piemēram, apsveriet ar celtni paceltas kravas kustību apstākļos, kad celtņa strēle vienlaikus griežas ap savu asi. Kustīgais atskaites rāmis šajā gadījumā ir celtņa strēles. Attiecībā pret to slodze virzās taisni uz augšu - tā ir relatīva kustība. Tajā pašā laikā kopā ar izlici krava pārvietojas pa apļa loku attiecībā pret “fiksēto” Zemi - tā ir pārnēsājama kravas kustība.

Novērotājs, kas stāv uz Zemes, redz absolūto kravas kustību, ko veido divas kustības, kas notiek vienlaicīgi.

Cilvēka kustība pa eskalatora kustīgajām kāpnēm ir arī sarežģīta: cilvēka kustība attiecībā pret pakāpieniem ir relatīva, un viņa kustība kopā ar pakāpieniem attiecībā pret tuneļa fiksētajām sienām ir pārnēsājama. Absolūta būs cilvēka kustība attiecībā pret nekustīgām sienām.

Tādējādi punkta absolūtā kustība ir divu kustību kombinācija: relatīvā un figurālā. Šajā gadījumā ir absolūtas, relatīvas un pārnēsājamas trajektorijas un attiecīgi vienādi punkta ātrumi un paātrinājumi.

§21. Punkta ātrumu un paātrinājumu saskaitīšana
sarežģītā kustībā

Vairākos gadījumos punkta absolūtā kustība tiek noteikta no dotajām relatīvajām un figurālajām kustībām. Dažkārt ir dota absolūtā un viena no sastāvošām kustībām, bet ir jānosaka otra veidojošā kustība.

Apskatīsim, kā tiek noteikta punkta absolūtā kustība (t.i., absolūtās nobīdes, ātrums un paātrinājums), ja tā relatīvās un pārvietojamās kustības ir taisnas un vērstas viena pret otru leņķī. Ļaujiet kravu M pārvietojas uz leju slīpajā plaknē un kādu laiku D t pārvietojas attiecībā pret to ar D Srel (72. att.).

/text/categ/nauka.php" class="myButtonNauka">Iegūt pilnu tekstu

http://pandia.ru/text/80/153/images/image574.jpg" width="268" height="83 src=">

Mēs dalām katru vienādojuma (37) daļu ar laiku D t, kuras laikā notika kustība, un režija D t® 0, mēs iegūstam izteiksmi:

http://pandia.ru/text/80/153/images/image576.gif" width="101" height="24 src=">. (38)

Tāpēc, ja relatīvās un translācijas kustības ir taisnas, punkta absolūtais ātrums katrā laika momentā tiek definēts kā relatīvā un translācijas ātruma ģeometriskā summa. Grafiski punkta absolūto ātrumu var noteikt ar paralelogramu vai trijstūra likumu (74. att., a un b). ).

http://pandia.ru/text/80/153/images/image578.gif" width="251" height="31 src=">

METODOLOĢISKIE NORĀDĪJUMI UN KINEMĀTIKAS PROBLĒMU RISINĀŠANAS PIEMĒRI

Ķermeņa griešanās ap fiksētu asi kinemātika

1. Īsa informācija no teorijas

Vienādojums rotācijas kustība stingra ķermeņa ap fiksētu asi ir forma

Leņķis tiek skaitīts no izvēlētā sākuma punkta. Tajā pašā laikā leņķiem, kas uzzīmēti pulksteņrādītāja kustības virzienā, tiek piešķirta mīnusa zīme, bet pretējā virziena leņķiem - plus zīme.

Rotācijas leņķi izsaka radiānos. Dažreiz griešanās leņķi nosaka apgriezienu skaits N. Attiecības starp un N Nākamais .

Ķermeņa leņķiskais ātrums:

Atvasinājuma zīme ļauj noteikt, vai ķermeņa rotācija notiek griešanās leņķa rādījuma pozitīvajā virzienā (plus zīme) vai pretējā virzienā (mīnus zīme). Leņķiskā ātruma mērvienība ir radiāni sekundē (vai 1/s).

Dažreiz leņķisko ātrumu raksturo apgriezienu skaits minūtē, un to apzīmē ar burtu n. Attiecības starp un n ir forma

Ķermeņa leņķiskais paātrinājums:

(42)

Atvasinājuma zīme ļauj noteikt, vai ķermeņa rotācija noteiktā laika momentā ir paātrināta vai palēnināta. Ja zīmes un ir vienādas, ķermenis griežas ātri, un, ja to pazīmes atšķiras, tas griežas lēni. mērvienība leņķiskais paātrinājums- radiāns sekundē kvadrātā (vai 1/s 2).

To ķermeņa punktu trajektorijas, kas neatrodas uz rotācijas ass, ir apļi ar centriem uz rotācijas ass un rādiusiem, kas vienādi ar īsāko attālumu no šiem punktiem līdz rotācijas asij.

Jebkura ķermeņa punkta ātruma modulis attālumā h no rotācijas ass (18. att.), nosaka pēc formulas

. (43)

Punkta ātrums ir virzīts pa pieskares riņķa līnijai, ko apraksta punkts kustības virzienā.

Jebkura ķermeņa punkta paātrinājums sastāv no diviem komponentiem - rotācijas un asas paātrinājumi:

Punkta rotācijas paātrinājuma moduli nosaka pēc formulas

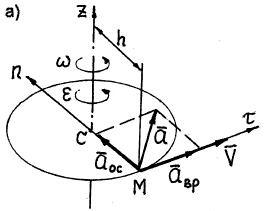
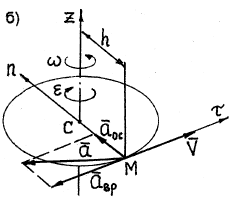
Rīsi. astoņpadsmit

Rotācijas paātrinājums ir vērsts tangenciāli uz punkta aprakstīto apli tādā pašā virzienā kā tā ātrums, ja ķermeņa rotācija ir paātrināta (18. att., a) un virzienā, kas ir pretēja ātrumam, ja griešanās ir lēna. (18. att., b).

Modulis asas paātrinājumu nosaka pēc formulas

Osemostimelnoepaātrinājums vienmēr tiek virzīts pa apļa rādiusu no punkta līdz apļa centram (18. att.).

Punkta pilna paātrinājuma moduli nosaka pēc formulas

(46)

2. Galvenie ķermeņa rotācijas ap asi kinemātikas problēmu veidi

Atkarībā no tā, kas ir norādīts problēmas stāvoklī un kas ir jānosaka, tiek izdalīti šādi divi galvenie problēmu veidi.

1. Tiek pētīta ķermeņa kustība kopumā. Šajās problēmās vispirms jāiegūst likumi (40)–(42) un, izmantojot attiecības starp tiem, jānosaka nepieciešamā vērtība (sk. 17. un 18. piemēru).

2. Nepieciešams noteikt atsevišķu ķermeņa punktu ātrumus un paātrinājumus. Lai atrisinātu šāda veida problēmas, vispirms ir jānosaka visa ķermeņa kustības kinemātiskās īpašības kopumā, t.i. atrast un . Pēc tam, izmantojot formulas (43), (44), (45), (46), nosaka ķermeņa punktu ātrumus un paātrinājumus (skat. 19. piemēru).

17. piemērs.Lidmašīnas propelleris, veicot 1200 apgr./min, pēc dzinēja izslēgšanas apstājas pēc 8 s. Cik apgriezienus šajā laikā veica dzenskrūve, ja uzskatām, ka tā rotācija ir tikpat lēna?

Risinājums:

Pirmkārt, mēs iegūstam dzenskrūves rotācijas likumus (40), (41) un (42). Atbilstoši problēmas stāvoklim dzenskrūve griežas tikpat lēni, no tā izriet, ka

Tāpēc

(48)

Sākotnējais leņķiskais ātrums lēnas rotācijas laikā būs tāds, kāds bija dzenskrūvei pirms dzinēja izslēgšanas. Sekojoši, . Apstāšanās brīdī plkst t 1 = 8 sek. ķermeņa leņķiskais ātrums. Aizvietojot šīs vērtības vienādojumā (47), mēs iegūstam

No šejienes

Ja mēs apzīmējam laikā izgatavoto propelleru skaitu t 1 apgrieziens cauri N 1 , tad griešanās leņķis tajā pašā laikā būs vienāds ar

Aizvietojot atrastās vērtības vienādojumā (48), mēs iegūstam

No šejienes revolūcijas.

18. piemērs.Atrodiet ķermeņa rotācijas likumu ap asi, ja ir zināmi šādi dati: leņķiskais ātrums mainās proporcionāli t 2 , sākotnējais griešanās leņķis ir rad, priekš dots brīdis laiks t 1 = 3 s leņķiskais paātrinājums 1/s 2 .

Risinājums:

Atbilstoši uzdevuma stāvoklim leņķiskā ātruma modulis mainās proporcionāli t 2. Nezināmo proporcionalitātes koeficientu apzīmē ar burtu k, mums ir

Ļaujiet mums atrast, ņemot laika atvasinājumus abām vienlīdzības pusēm (49),

Definēsim koeficientu k no nosacījuma, ka t 1 = 3 sek. leņķiskais paātrinājums 1/s 2 : vai

Aizvietojošā vērtība k vienādojumā (49), iegūstam

Ņemot to vērā, mums būs

Reizinot abas šī vienādojuma puses ar dt un integrējot, mēs atrodam

Sākotnējā brīdī plkst t = 0, = 2 rad, tāpēc c = 2.

Pa šo ceļu, radiāns.

19. piemērs.Paātrinājuma periodā elektromotora rotors griežas atbilstoši likumam, kur t sekundēs, rad.

Nosakiet 4. sekundes beigās lineārais ātrums, rotācijas, asas un kopējais paātrinājums punktā, kas atrodas uz rotora loka, ja rotora diametrs D= 40 cm.

Risinājums:

Saskaņā ar doto rotora rotācijas vienādojumu mēs atrodam tā leņķisko ātrumu un leņķisko paātrinājumu, .

Aizvietojošā vērtība t 1 = 4 sekundes izteiksmē un , mēs atrodam

1/s,

1/s2.

Noteiksim lineārā ātruma, rotācijas un asas paātrinājumi tajā pašā laika momentā saskaņā ar formulām (43), (44) un (45)

Rotora loka punkta kopējo paātrinājuma moduli nosaka pēc formulas (46)

3. Ātrumu un paātrinājumu noteikšana gadījumos, kad rotējošs ķermenis ir daļa no dažādiem mehānismiem

Apsveriet mehānismus ar saišu translācijas un rotācijas kustību. Problēmas risinājums sākas ar to saites punktu ātruma noteikšanu, kuriem ir dota kustība. Pēc tam apsveriet saiti, kas ir pievienota pirmajai saitei utt. Rezultātā tiek noteikti visu mehānisma saišu punktu ātrumi. Punktu paātrinājumus nosaka tādā pašā secībā.

Rotācijas pārnešanu no viena rotējoša korpusa, ko sauc par galveno, uz otru, ko sauc par vergu, var veikt, izmantojot berzes vai zobratu transmisiju (19. att.).

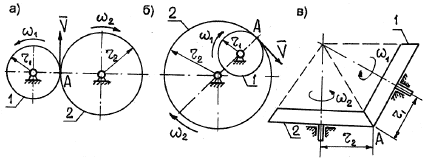
Rīsi. 19

Berzes transmisijā rotācija tiek pārnesta berzes spēka iedarbības dēļ saskarē esošo riteņu saskares punktā, pārnesumu transmisijā - no zobu saķeršanās. Piedziņas un dzenošo riteņu griešanās asis var būt paralēlas (19. att., a, b) vai krustoties (19. att., c). Aplūkotajos gadījumos punktu lineārie ātrumi BET riteņu kontakti ir vienādi, to moduļi ir definēti šādi:

. (50)

No šejienes. (51)

Tas ir, berzes vai pārnesumu vilciena riteņu leņķiskie ātrumi ir apgriezti proporcionāli riteņu rādiusiem.

Pārvēršot rotācijas kustību par translāciju (vai otrādi), bieži tiek izmantota zobratu ieslēgšanās ar zobratu (20. att.). Šai pārraidei ir izpildīts šāds nosacījums: .

Papildus berzes un zobratu piedziņām ir rotācijas pārnešana, izmantojot elastīgu savienojumu (siksnu, trosi, ķēdi) (21. att.).

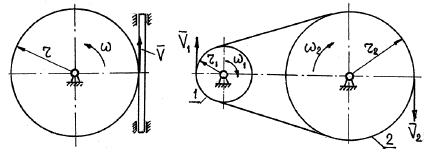
Rīsi. 20 att. 21

Tā kā visu siksnas punktu ātruma moduļi ir vienādi un siksna neslīd pa skriemeļu virsmām, tad attiecības (50) un (51) attiecas arī uz siksnas piedziņu.

20. piemērs.Domkrata mehānismā, kad rokturis ir pagriezts OA zobrati 1, 2, 3, 4, 5 vada bagāžnieku saule domkrats (22. att.).

Nosakiet statīva ātrumu, ja rokturis OA veic 30 apgriezienus minūtē n = 30 apgr./min.). Zobu zobratu skaits: z 1 = 6,z 2 = 24,z 3 = 8,z 4 = 32; piektā pārnesuma rādiuss r 5 = 4 cm.

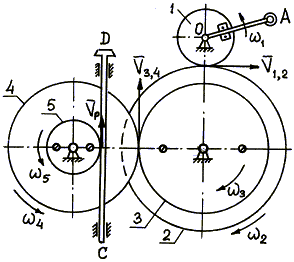
Rīsi. 22

Risinājums:

Kopš roktura OA ir stingri savienots ar 1. pārnesumu, tad pēdējais arī veic 30 apgr./min vai

1. un 2. pārnesumu saskares punktu ātruma moduļi ir vienādi abu riteņu punktiem un tiek noteikti pēc formulas (50)

Tādējādi (sk. arī (51)).

Tā kā zobu skaits ir proporcionāls riteņu rādiusiem, tad .

No šejienes

2. un 3. zobrati ir stingri savstarpēji savienoti, tāpēc

Riteņiem 3 un 4, kas ir ieslēgti, mēs varam rakstīt, pamatojoties uz (51).

No šejienes

4. un 5. zobrati ir savstarpēji stingri savienoti, tāpēc

Rack kontaktpunktu ātruma moduļi saule un 5. pārnesumi ir vienādi, tāpēc

vai

21. piemērs.Rack 1, pakāpju ritenis 2 ar rādiusiemR 2 un r 2 riteņa 3 rādiusiR 3 , kas savienots ar rādiusa vārpstu r 3 ir saderinājušies; uz vārpstas uztīta vītne ar slodzi 4 galā (23. att.). Reika kustas saskaņā ar likumu

Ņemot vērā:R 2 = 6 cm, r 2 = 4 cm, R 3 = 8 cm, r 3 \u003d 3 cm, (S- centimetros, t- sekundēs) BET- riteņa loka punkts 3,t 1 =3 s. Nosakiet: , , , laikā t = t 1 .

Apsveriet ciets, kas griežas ap fiksētu asi. Tad atsevišķi šī ķermeņa punkti aprakstīs dažādu rādiusu apļus, kuru centri atrodas uz rotācijas ass. Ļaujiet kādam punktam pārvietoties pa rādiusa apli R(6. att.). Tās pozīciju pēc laika intervāla Dr nosaka leņķis Dj. Elementāras (bezgalīgi mazas) rotācijas var uzskatīt par vektoriem (tos apzīmē ar vai ). Vektora modulis ir vienāds ar griešanās leņķi, un tā virziens sakrīt ar skrūves gala translācijas kustības virzienu, kura galva griežas punkta kustības virzienā pa apli, t.i., ievēro labās skrūves noteikumu (6. att.). Vektorus, kuru virzieni ir saistīti ar rotācijas virzienu, sauc par pseidovektoriem vai aksiālajiem vektoriem. Šiem vektoriem nav īpašu pielietojuma punktu: tos var zīmēt no jebkura rotācijas ass punkta.

Leņķiskais ātrums ir vektora lielums, kas vienāds ar ķermeņa griešanās leņķa pirmo atvasinājumu attiecībā pret laiku:

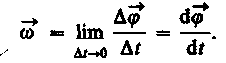
Vektors ir vērsts pa griešanās asi pēc labās skrūves noteikuma, t.i., tāpat kā vektors (7. att.). Leņķiskā ātruma izmērs , un tā mērvienība ir radiāns sekundē (rad/s).

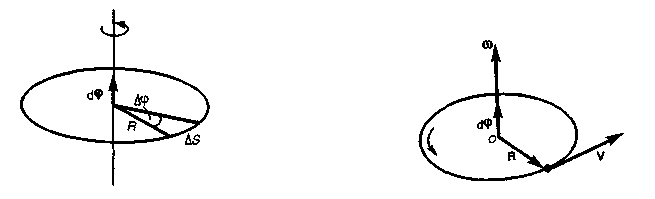
Rīsi. 6 att. 7

Punkta lineārais ātrums (skat. 6. att.)

.

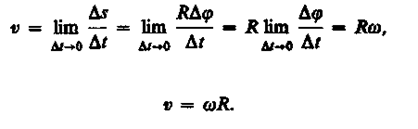
Vektora formā lineārā ātruma formulu var uzrakstīt kā krustojumu:

Šajā gadījumā vektora reizinājuma modulis pēc definīcijas ir vienāds ar eaKap(shK), un virziens sakrīt ar labās skrūves translācijas kustības virzienu, kad tā griežas no uz R.

Ja w = const, tad rotācija ir vienmērīga un to var raksturot ar rotācijas periodu T- laiks, kurā punkts veic vienu pilnīgu apgriezienu, t.i., pagriežas leņķī 2p. Tā kā laika intervāls Dt = T atbilst Dj = 2p, tad w = 2p/T, kur

Pilnu apgriezienu skaitu, ko ķermenis veic tā vienmērīgās kustības ps apļa laikā, laika vienībā sauc par griešanās frekvenci:

Leņķiskais paātrinājums ir vektora lielums, kas vienāds ar pirmo leņķiskā ātruma atvasinājumu attiecībā pret laiku:

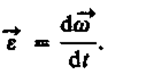
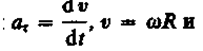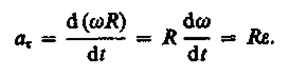Paātrinājuma tangenciālā sastāvdaļa

Normāla paātrinājuma sastāvdaļa

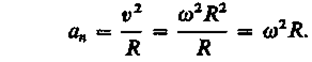
Kad ķermenis griežas ap fiksētu asi, es virzu leņķiskā paātrinājuma vektoru pa rotācijas asi uz leņķiskā ātruma elementārā pieauguma vektoru. Ar paātrinātu kustību vektors tiek līdzvirzīts uz vektoru (8. att.), ar lēnu kustību ir pretējs tam (9. att.).

Rīsi. 8 att. 9

Tādējādi attiecības starp lineāro (ceļa garumu s, rādiuss šķērsoja punktu pa apļa loku R, lineārais ātrums v, tangenciālais paātrinājums a t,normāls paātrinājums a n) un leņķiskās vērtības (griešanās leņķis j , leņķiskais ātrums w , leņķisko paātrinājumu e) izsaka ar šādām formulām:

Vienmērīgi mainīgas punkta kustības gadījumā pa apli (e-const)

kur w 0 ir sākotnējais leņķiskais ātrums.

Uzdevumi

1.1.Ķermeņa noietā ceļa atkarību no laika uzrāda vienādojums s=A+Bt+Ct 2 +Dt 3(C \u003d 0,1 m/s 2, D=0,03 m/s 3). Noteikt: 1) laiku pēc kustības sākuma, pēc kura paātrinājums a korpuss būs vienāds ar 2 m / s 2;

2) vidējais paātrinājums<а>ķermenim šajā laika periodā.

1.2. Neņemot vērā gaisa pretestību, nosakiet leņķi, kādā ķermenis tiek izmests pret horizontu, ja ķermeņa maksimālais augstums ir vienāds ar 1/4 no tā lidojuma diapazona.

1.3. Ritenis ar rādiusu R = 0,1 m griežas tā, ka leņķiskā ātruma atkarību no laika nosaka vienādojums w = 2 plkst+ 5Bt 4 (A = 2 rad/s 2 un AT= 1 rad/s 5). Nosaka kopējo riteņa loka punktu paātrinājumu līdz t = 1 s pēc griešanās sākuma un riteņa apgriezienu skaitu šajā laikā. [a \u003d 8,5 m/s 2; N=0,48]

1.4. Normālo paātrinājumu punktam, kas pārvietojas pa apli ar rādiusu r = 4 m, nosaka vienādojums a n \u003d A + Bt + Ct 2(A \u003d 1 m/s 2, B = 6 m/s 2, C \u003d 3 m/s 2). Noteikt: 1) punkta tangenciālo paātrinājumu; 2) laika punkta noietais ceļš t1=5 s pēc kustības sākuma; 3) kopējais paātrinājums laikam t 2 =1 s.

1.5.Riteņa griešanās biežums pie vienlīdz lēnas kustības t = 1 min samazinājās no 300 līdz 180 min -1. Noteikt: 1) riteņa leņķisko paātrinājumu; 2) riteņa veikto pilno apgriezienu skaits šajā laikā.

1.6.Disks ar rādiusu R=10 cm griežas ap fiksētu asi tā, ka diska rādiusa griešanās leņķa atkarību no laika uzrāda vienādojums j =A+3t+Ct2+Dt3(B = 1 rad / s, C = 1 rad / s 2, D \u003d 1 rad / s 3). Nosakiet punktiem uz riteņa loka līdz otrās sekundes beigām pēc kustības sākuma: 1) tangenciālais paātrinājums %; 2) normāls paātrinājums a n; 3) pilns paātrinājums a.

1.56. Punkts pārvietojas pa apli ar rādiusu R = 2cm. Ceļu pret laiku uzrāda vienādojums s = C/3, kur C = 0,1 cm/s3. Atrodiet normālo an un tangenciālu punkta paātrinājumam brīdī, kad punkta lineārais ātrums ir v = 0,3 m/s.
Risinājums:

1.57. Punkts pārvietojas pa apli tā, ka ceļa atkarību no laika uzrāda vienādojums s = A-Bt + Ct^2, kur B = 2 m/s un C = 1 m/s2. Atrodiet punkta lineāro ātrumu v, tā tangenciālu pie normālā an un kopējo paātrinājumu a pēc laika t = 3 s pēc kustības sākuma, ja zināms, ka pie t' = 2 s punkta a normālais paātrinājums 'n = 0,5 m/s2.
Risinājums:

1.58. Atrodiet riteņa leņķisko paātrinājumu s, ja ir zināms, ka pēc laika t = 2 s pēc kustības sākuma uz loka esošā punkta kopējais paātrinājuma vektors ar tā lineārā ātruma vektoru veido leņķi a = 60°.
Risinājums:

1.59. Ritenis griežas ar leņķisko paātrinājumu E=2 rad/s2. Pēc laika t \u003d 0,5 s pēc kustības sākuma kopējais riteņa paātrinājums ir \u003d 13,6 cm / s. Atrodiet riteņa rādiusu R.
Risinājums:

1.60. Ritenis ar rādiusu R = 0,1 m griežas tā, ka riteņa rādiusa griešanās leņķa atkarību no laika nosaka vienādojums (p = A + Bt + Ct^2, kur B = 2rad/s un C = 1 rad/s^3. Punktiem, kas atrodas uz riteņa loka, atrodiet pēc laika t = 2 s pēc kustības sākuma:
a) leņķiskais ātrums w;
b) lineārais ātrums v;
c) leņķiskais paātrinājums E ;
d) tangenciāls pie un parastajiem a paātrinājumiem.
Risinājums: